一种舰船流场特性计算方法研究*
张永坤 王树乐
(91439部队 大连 116041)
一种舰船流场特性计算方法研究*
张永坤 王树乐
(91439部队 大连 116041)
以DTMB5415为研究对象,采用RANS方法结合VOF模型,研究了网格因素以及湍流模型对阻力、波形和流场预报精度的影响。首先设计了粗糙、中等和精细共三套网格,分别进行兴波流场计算,通过比较试验测试的阻力和波形数据,确定中等网格划分方式既能保证计算的准确性又能保持较高的计算效率。其次选择三种湍流模型,对总阻力及舷侧波高进行数值计算,SST k-ω湍流模型在保证计算效率的情况下可满足计算精度要求。最后采用中等网格划分以及SST k-ω模型进行计算,并同试验测量结果进行比对,结果表明船侧表面附近数值计算波形分布与试验结果基本一致。
流场; 计算网格; 流体体积函数; 数值计算
Class Number U661.2
1 引言
船体是一个极其复杂的曲面,由于流体的粘性作用,船舶航行时产生边界层,形成非常不均匀的三向伴流场。船舶伴流场的准确获取是螺旋桨设计、船体水动力和噪声性能预报等研究的基础条件。鉴于此,开展水面舰船伴流场数值计算研究,分析舰船阻力、特征截面伴流场分布,对于提高水面舰船水动力性能的预报精度具有重要意义。使用CFD方法进行流场计算时,首先要将计算域进行离散,数值计算是在离散的网格节点上满足流体力学方程,因此网格分辨率对数值计算结果有较大的影响。网格数太少,太稀疏难以得到精确的结果[1],网格数太大、过密又会增加计算量。
本文以DTMB5415为研究对象,采用RANS方法[2~7]结合VOF模型[9~10]研究了网格和湍流模型等因素对阻力、波形和流场预报精度的影响。首先进行网格依赖性研究,采取全结构化网格划分方法,固定某种湍流模型,设计了粗糙、中等和精细共三套网格,分别进行兴波流场计算,通过比较试验测试的阻力和波形数据,确定中等网格划分既能保证计算的准确性又能保持较高的计算效率。在此基础上,选取理论发展比较完善、船舶粘性流场数值计算常用的几种湍流模型,RNGK-ε和SST k-ω湍流模型和雷诺应力模型进行湍流模型的影响研究,通过与试验数据的对比,三种湍流模型均能较准确地预报该船的阻力,而在船体舷侧波形预报上,SST k-ω湍流模型和雷诺应力模型更具有优势。
2 计算对象
本文采用DTMB5415为研究对象,进行数值计算方法的验证。DTMB5415为美国海军驱逐舰(DDG51)的模型,自1996年后,DTMB5415成了ITTC用于船舶CFD水动力计算验证的表准模型之一,意大利和美国对它做了一系列试验,且公布了完整的试验报告,有详细的阻力、波形和流场试验数据。其外形轮廓如图1所示,主尺度见表1。
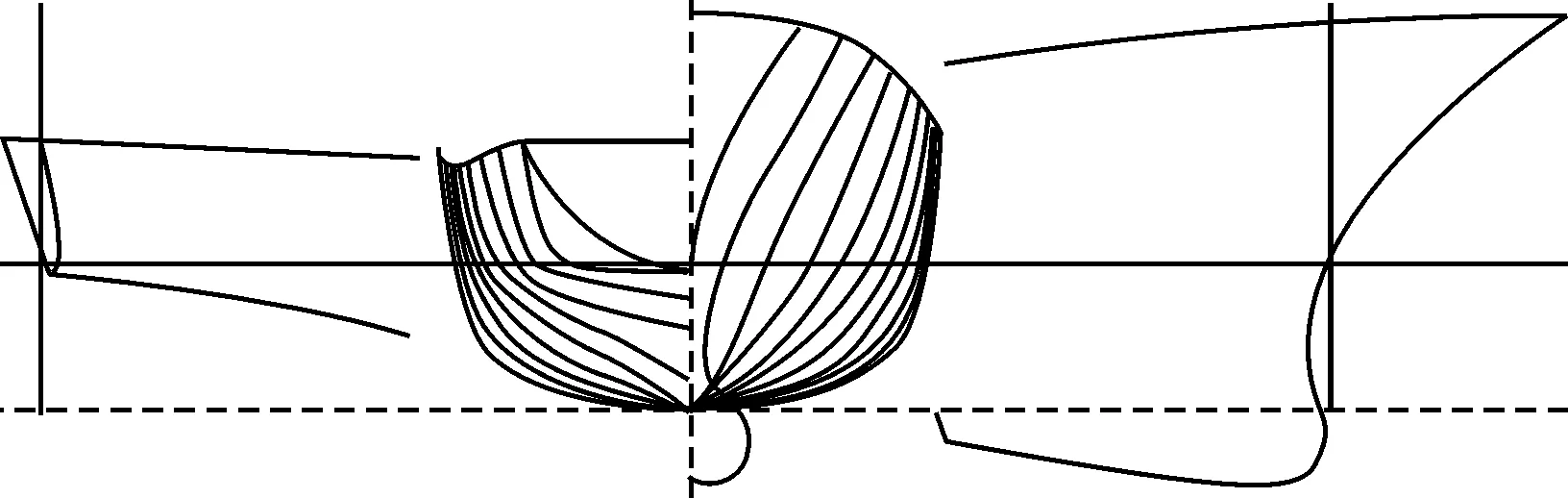
图1 DTMB5415的外形轮廓
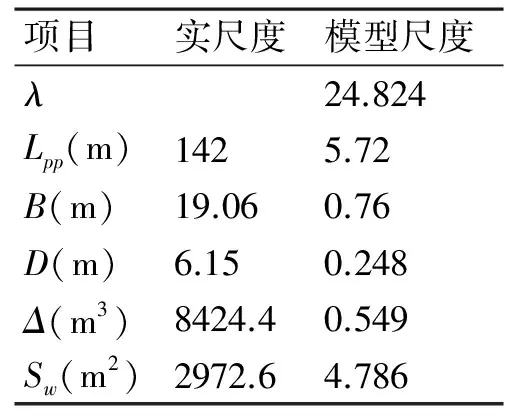
项目实尺度模型尺度λ24.824Lpp(m)1425.72B(m)19.060.76D(m)6.150.248Δ(m3)8424.40.549Sw(m2)2972.64.786
根据哥德堡2010会议公布的测试案例,选取的计算状态为:固定升沉1.82×10-3,纵倾(-0.108°),航速2.097m/s,雷诺数为1.19×107,长度傅汝德数为0.28。计算平台为ANSYS FLUENT14.0。
3 计算方法
计算考虑兴波,即带自由液面,自由液面由于要考虑空气和水的相互作用,所以属于多项流问题。采用VOF方法处理自由液面问题,以流体占据网格单元体积份额的途径来跟踪自由面演化,具体算法使用固定网格系统捕捉多种相参混流体的交界面,所有流体满足同一动量方程,在整个计算区域上跟踪每一种流体在每个计算单元中的体积分数。
假设第q种流体在单元中的体积分数为αq,则存在以下三种可能: 1)αq=0,单元内不存在第q种流体; 2)αq=1,单元内充满第q种流体; 3) 0<αq<1,单元内存在不同流体的交界面。
在VOF方法中,αq定义一个单元中流体所占有的体积分数,用αq还可以确定交界面的位置,因为在交界面法向上αq变化最快。在确定交界面法向以及体积分数αq的值后,单元中就可以确定一条分割线,用来近似表达两种液体的交界面。
为了跟踪流体之间界面的位置,需要求解体积分数的连续性方程,对q种流体有:
(1)
各种流体体积分数满足式(2):
(2)
每个控制体中,流体密度由体积分数平均得到:
ρ=∑αqρq
(3)
其它流体性质如粘性也由类似的方法计算。
在整个计算区域只要计算单个动量方程,动量方程通过密度ρ和粘性系数μ依赖于各相流体的体积分数,动量方程如式(4):
(4)
对于其它输运量,如湍动能、耗散率或者雷诺应力等,所有流体也只要求解一组输运方程。
微分方程采用有限体积法离散时,数值计算必须控制各个面上的对流和扩散通量,以便和单元内源相平衡,这里对单元表面通量的计算采用的是精度较高的几何重构法。几何重构法使用分段线性的方法描绘流体之间的界面,它假设两种流体之间的界面在每个单元内有个线性斜面,并使用这个线性形状来计算穿过单元面的流体对流。
4 湍流模型及边界条件设置
4.1 船体网格划分
采用全结构化网格离散计算域[11],网格采用H-O拓扑形式,在球鼻艏和艉部流动变化较大的区域进行加密,保证船中近壁面第一层网格单元y+=80左右,船体表面网格如图2所示。

图2 DTMB5415表面网格划分
自由液面兴波流场的计算区域从静水面处分为两个部分,水域和空气层。上游入口离船艏1倍船长,下游出口离船尾2.5倍船长,空气层的厚度为1.5倍吃水高度,外侧面离船中1倍船长。
4.2 边界条件设置
边界条件的设置如下:上游入口采用速度入口,给定均匀来流的速度值;下游出口采用FLUENT提供的用户接口,编写用户UDF函数,给定静压出口,忽略扰动;上边界、侧边和中间面均采用对称面边界条件,根据计算经验,上边界和侧边采取对称面与无扰动的速度来流条件效果是一样的;在船体表面定义无滑移、不可穿透的边界条件。
4.3 湍流模型选取
湍流模型对船舶粘性流场的计算精度有重要的影响。选取理论发展比较完善、船舶粘性流场数值计算常用的几种湍流模型,RNGK-ε和SST k-ω湍流模型和雷诺应力模型。
1) RNG k-ε模型
为了准确描述强旋流或带有弯曲壁面的流动,Yakhot等提出了重整化群k-ε(即RNG k-ε)模型,该模型在时均连续方程和动量守恒方程的基础上,引入湍动能k和湍动耗散率ε的方程,再建立湍动粘度μt与k和ε的关系式,使方程组封闭。
2) SST k-ω模型
改进二:热源改酒精灯为恒温调奶器(温度可在37~100℃之间任意恒定);改水浴加热为80℃恒温直接加热;改分组脱色为全班集中脱色。恒温调奶器为内热热源,没有明火,除去了明火热源可能点燃酒精引发火灾的安全隐患。加热温度恒定在酒精沸点温度之下,因此不会出现因酒精沸腾飞溅到学生身上造成的意外伤害。温度恒定在酒精沸点之下,可以减慢酒精气化速度,节约酒精的同时也加快了脱色速度。
为了准确求解分离流问题,Menter提出了SST k-ω湍流模型,该模型对壁面处流场应用k-ω模型而对总体流动则应用k-ε模型求解,两模型间的过渡通过混合函数完成。
3) 雷诺应力模型
涡粘模型采用各向同性的湍动粘度来计算湍流应力,这种假设往往导致此类模型难以准确考虑旋转流动和流动方向表面曲率变化的影响,当流场中存在高曲率流动、逆压梯度、分离流及强旋转流动时,湍动粘度的各向异性影响较大,导致应用涡粘模型模拟的流场分布与实验结果明显不符。为了克服这个缺点,需要对RANS方程中的Reynolds应力项直接建立微分方程式进行求解,以此得到Reynolds应力的各个分量值。
采用有限体积法离散控制方程和湍流模式,压力项采用body-forced-weighted格式离散,其他项均采用二阶迎风格式离散,体积分数采用几何重构方案,压力速度耦合迭代采用SIMPLEC方法。
5 结果分析
5.1 网格依赖性研究
为了研究网格依赖性,共设计了粗糙、中等、精细共三套网格,三套网格的拓扑形式完全一致,仅仅是长度方向、展向和腰身方向的节点数量不一致,三套网格的加细率rG=1.4142,三套网格的具体设置如表2所示。
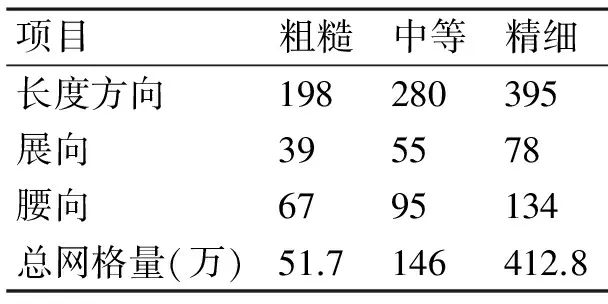
表2 三套网格节点布置情况
图3为中等网格总阻力系数收敛的时间历程曲线,从图中可以看出计算时间达到10s后,总阻力系数成比较稳定的周期性变化,取稳定周期内总阻力的时历平均值作为计算结果。
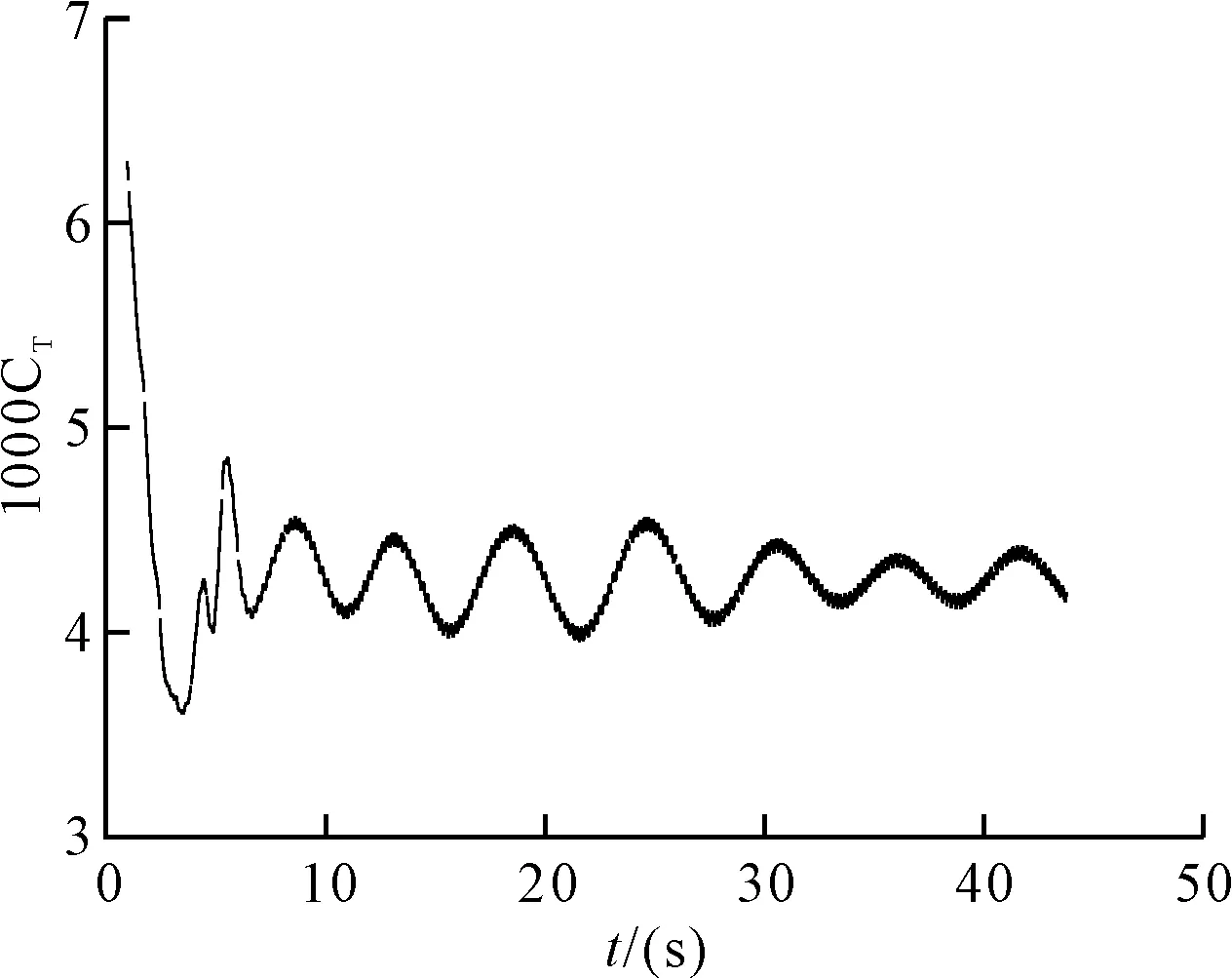
图3 总阻力系数收敛曲线
三套网格数量下,Fn=0.28时DTMB5415裸船体的总阻力系数数值计算结果与试验数据的对比如表3所示。
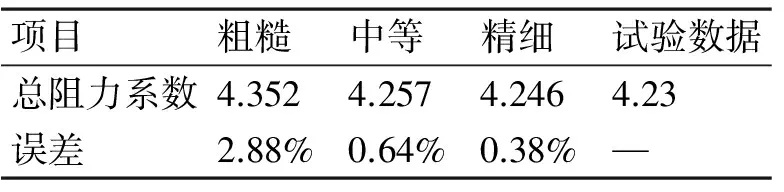
表3 不同网格数量的总阻力系数计算结果与试验数据的对比
从表3中可以看出:随着网格数量的增加,阻力计算精度也相应增加。在此傅汝德数下,中等网格的计算精度已足够工程应用范围。
采用26届ITTC推荐规程对阻力计算的网格收敛性进行判断。粗糙网格计算结果记为sGC;中等网格计算结果记为sGM;精细网格计算结果记为sGF;计算粗糙网格与中等网格、中等网格与精细网格结果之差为
εGMC=SGM-SGC=4.257-4.352=-0.095
εGFM=SGF-SGM=4.246-4.257=-0.011
网格收敛因子:
由于网格收敛因子〈RG〉小于1,说明计算网格的收敛性得到满足,表明计算网格数越大数值计算结果越精确,不确定度越小。
进一步比较波形对网格数量的依赖性。图4和图5分别为三种网格数量下y/LPP=0.082,y/LPP=0.172船侧波高的计算值与试验值的对比。
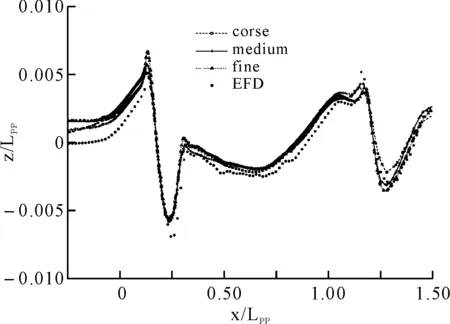
图4 y/LPP=0.082时船体舷侧波高沿船长分布曲线

图5 y/LPP=0.172时船体舷侧波高沿船长分布曲线
从图中可以看出:当非常靠近船体表面时,即y/LPP=0.082,三套网格均能很好地模拟出船体舷侧波高沿船长的分布,波峰和波谷的位置捕捉得非常精确,具体幅值稍有差异,整体来说,精细网格分布效果最好。而稍微远离船体表面,即y/LPP=0.172时,它们之间的差异变大,粗糙网格模拟的船体舷侧波高在船中部分已不能捕捉二次小波谷,在艉部捕捉的波谷值也过小,而中等和精细网格依然能较好地模拟船体舷侧波高沿船长的分布,波峰和波谷的位置非常精确,幅值大小也相差无几。
综合阻力和兴波波形的计算结果,同时考虑到计算资源,湍流模型研究可采取中等网格划分形式。
5.2 湍流模型影响研究
1) 总阻力
以DTMB5415为对象,采取中等网格划分,分别结合以上三种湍流模型对傅汝德数Fr=0.28时的舰船兴波流场进行求解。计算结果如表4所示。
可以看出:RNGK-ε模型比试验值稍低而雷诺应力模型则比试验值稍高,总体来说,三种湍流模型预报的总阻力精度均很高。
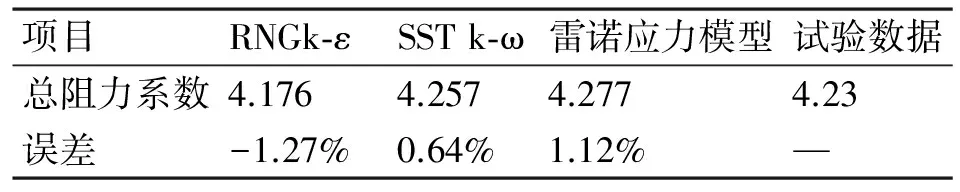
表4 不同湍流模型的总阻力系数计算结果与试验数据的对比
2) 船体舷侧波高
进一步比较这几种湍流模型计算得到的船体舷侧波高。图6和图7分别为三种湍流模型y/LPP=0.082,y/LPP=0.172船侧波高的计算值与试验值的对比。
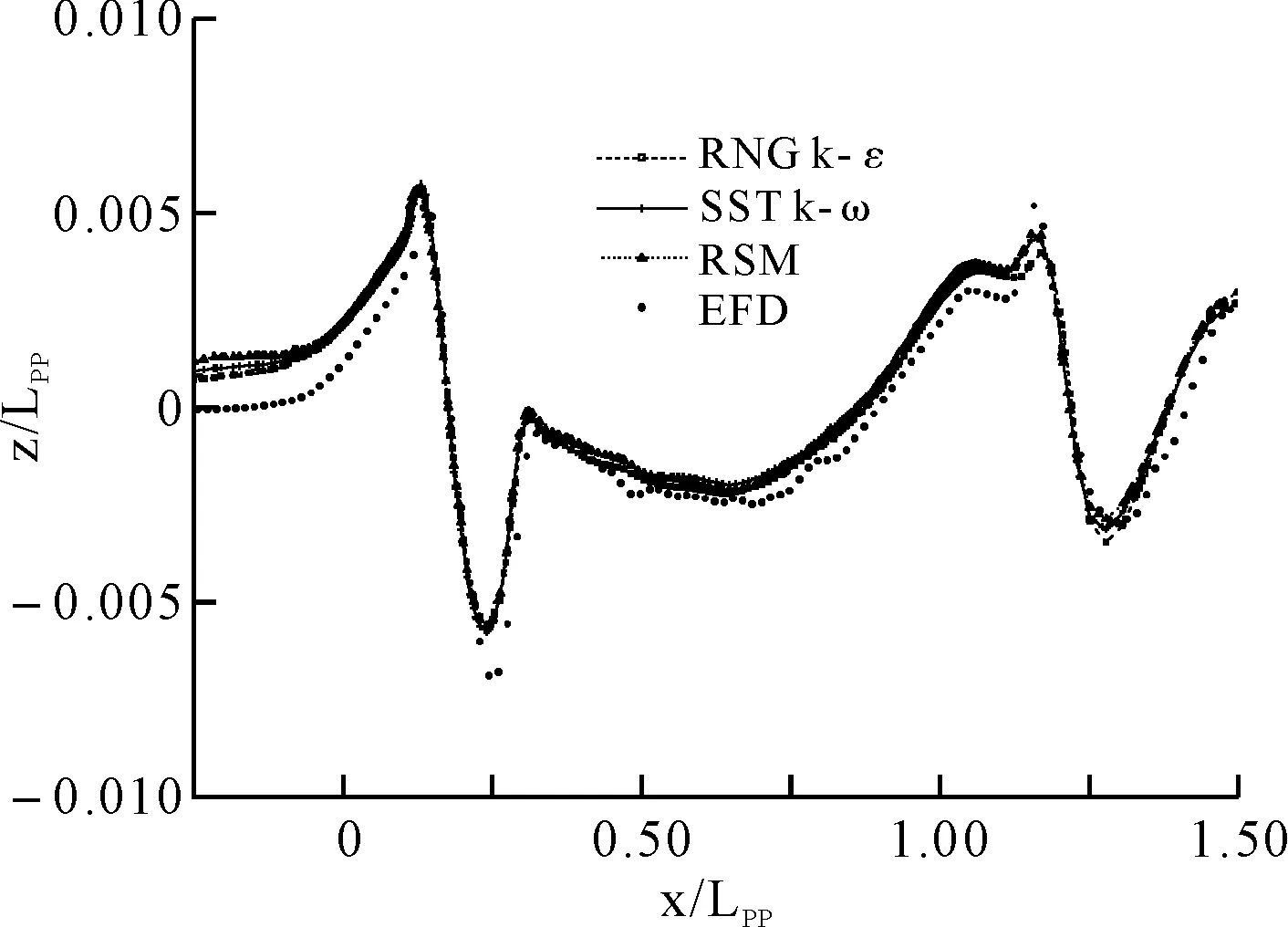
图6 y/LPP=0.082时船体舷侧波高沿船长分布曲线
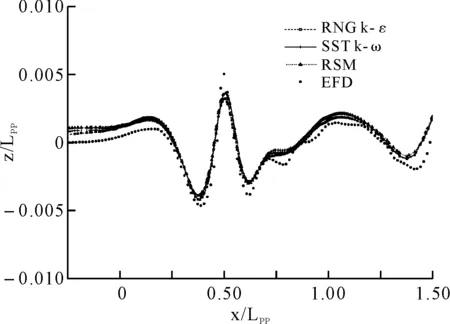
图7 型y/LPP=0.172时船体舷侧波高沿船长分布曲线
从图中可以看出:这三种湍流模型均能较好地预报船体舷侧波形,波峰和波谷的位置精确。总体而言,雷诺应力模型效果最好,SST k-ω模型次之,RNGK-ε模型稍微差点。综合计算精度和计算效率,可选择SST k-ω模型进行计算。
5.3 SST k-ω模型计算结果与试验值比对
由图8可知,在船侧表面附近,数值计算波形分布与试验数据吻合得相当好。而远离船体表面区域特别是艉部,由于网格的稀疏而导致波形消弱。
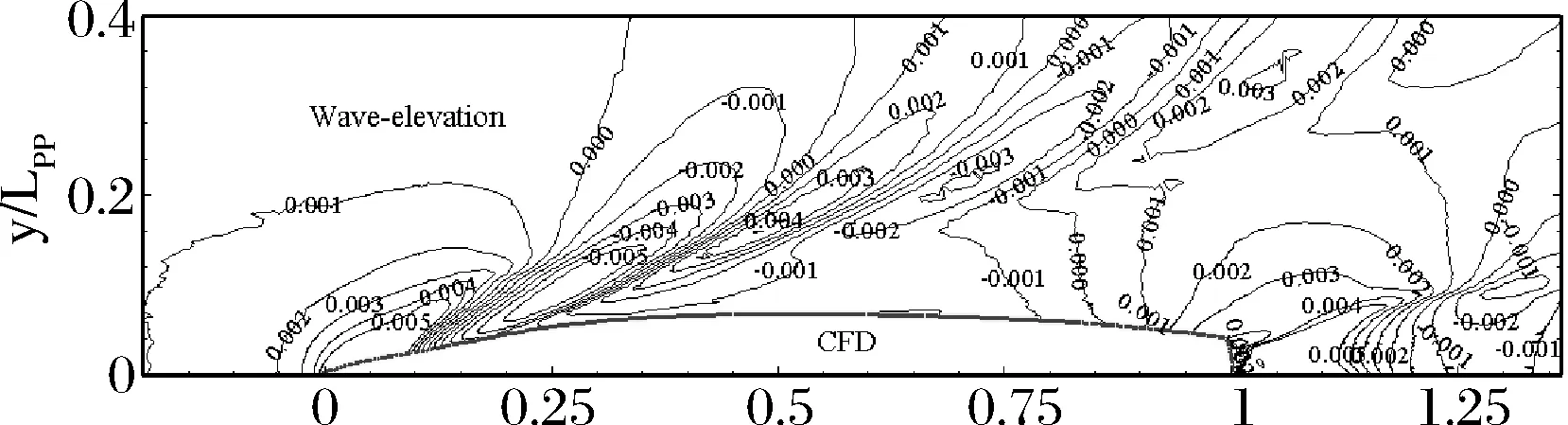

图8 SST k-ω模型计算波高等值线与试验数据的对比
观察图9可以发现,由于球鼻艏的存在而产生的漩涡向后发展,在此截面依然很强,这与试验观测是一致的;同时CFD还显示了此截面另外存在舭涡,而试验并未捕捉到这个现象。
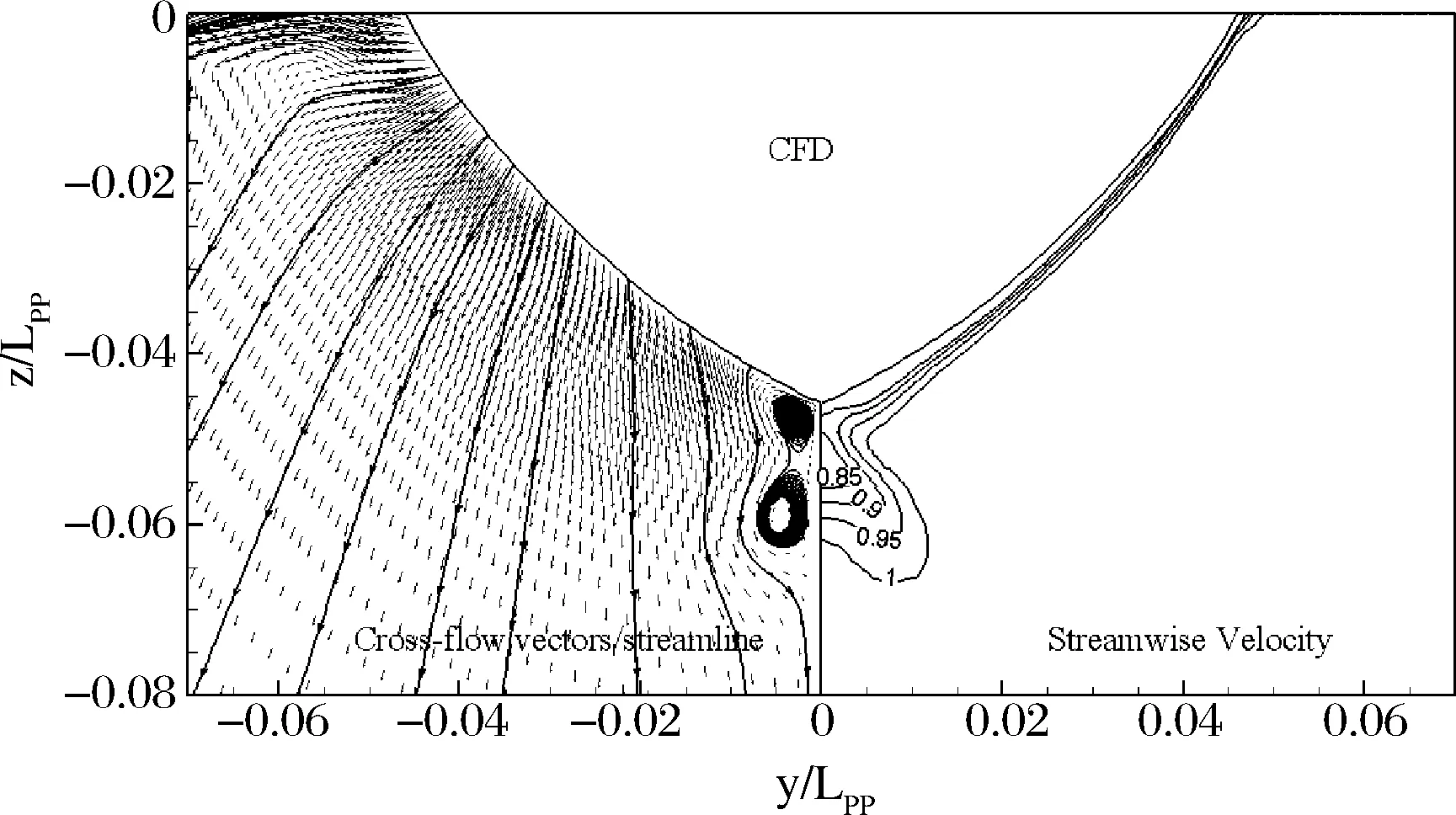
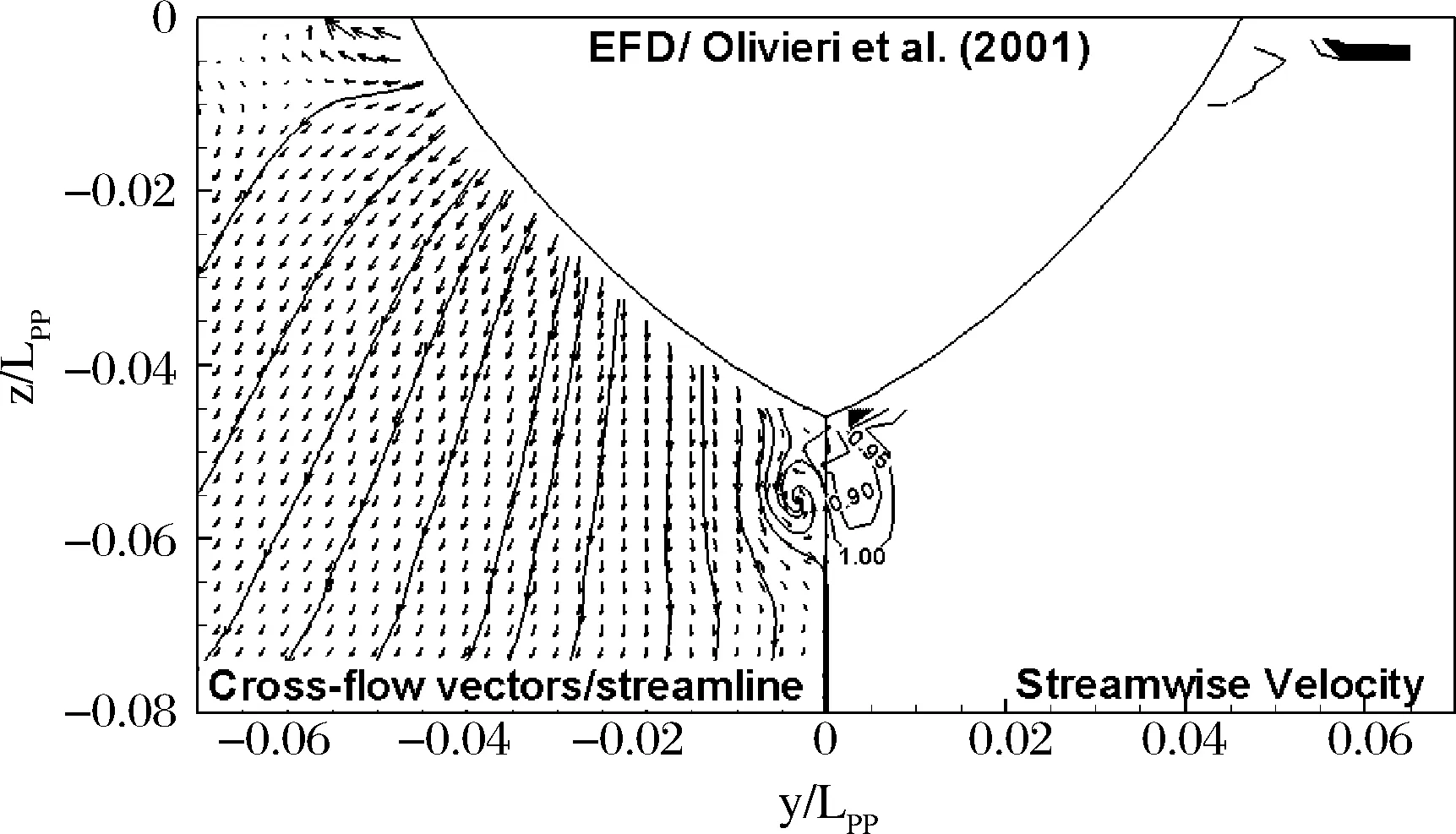
图9 x/LPP=0.2截面速度场的计算值与试验值的比较
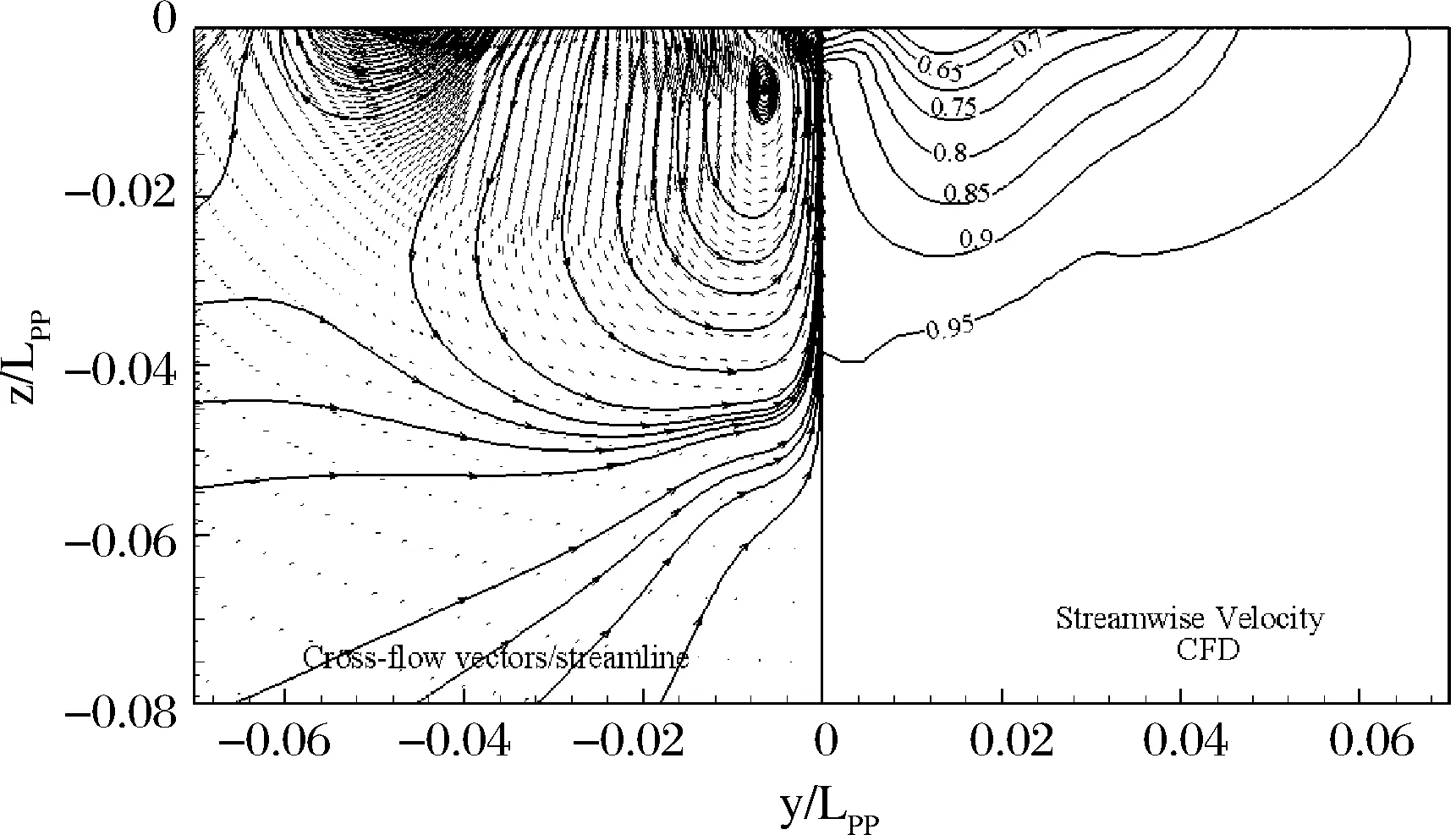
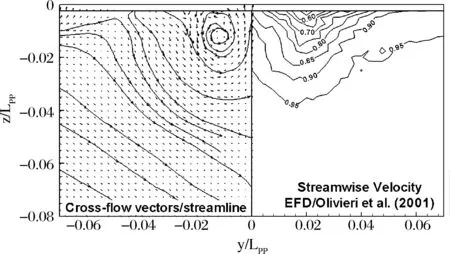
图10 x/LPP=1.1截面速度场的计算值与试验值的比较
图10为方艉正后方的某个截面。数值计算结果成功地捕捉到了方艉的流动现象,从图中可以看出,流动产生的主涡被正确地模拟。与试验结果相比,数值计算结果有两点差异。一是主涡中心位置更加靠近船体中纵剖面;二是船体底部的横向流动亦服从主涡的流动行为,而试验结果则显示该部分横向流动在涡流之外。产生这种现象的原因可能是CFD计算的流线更易遭受漩涡的影响。
6 结语
通过本文研究得到一些有意义的结论:
1) 计算网格数越大数值计算结果越精确,不确定度越小。
2) 稍微远离船体表面,粗糙网格模拟的船体舷侧波高在船中部分已不能捕捉二次小波谷,在艉部捕捉的波谷值也过小。
3) 通过比较试验测试的阻力和波形数据,中等网格划分既能保证计算的准确性又能保持较高的计算效率。在满足计算精度的条件下,采用中等数量计算网格可节省计算资源。
4) 就总阻力预报而言,RNGK-ε和SST k-ω湍流模型和雷诺应力模型预报精度都很高,满足计算要求。
5) 从预报船体舷侧波形来讲,三种湍流模型均能较好地预报,波峰和波谷的位置精确。总体而言,雷诺应力模型效果最好,SST k-ω模型次之,RNGK-ε模型稍微差点。综合考虑计算精度及计算效率,SST k-ω模型最优。
6) 选取DTMB5415计算对象,采用中等网格划分以及SST k-ω模型进行计算,计算结果同试验测量结果进行比对。结果表明船侧表面附近数值计算波形分布与试验结果一致,同时捕捉到球鼻艏导致的漩涡发展、舭涡以及方艉的流动等现象。
[1] 刘志华,熊鹰.潜艇流场数值计算网格与湍流模型选取[J].华中科技大学学报(自然科学版),2009,37(7):98-101.
[2] 黄振宇,周连第.带全附体潜艇尾流场的数值预报研究[J].中国造船,2001,42(2):6-11.
[3] 陈明周.基于CFD的潜艇尾流场波数预报研究[D].武汉:海军工程大学船舶与动力学院,2007.
[4] 吴召华,陈作钢.基于体积力法的船体自航性能数值预报[J].上海交通大学学报,2013,47(6):943-949.
[5] 沈兴荣,冯学梅,蔡荣泉.大型集装箱船桨舵干扰黏性流场的数值计算[J].船舶力学,2009,13(4):540-550.
[6] 邱辽原,侯国祥.轴对称回转体绕流场数值模拟[J].华中科技大学学报,自然科学版,2004,32(10):46-48.
[7] Stern F, Kim H T, Patel V C, et al. A viscous flow approach to the computation of propeller-hull interaction[J]. Journal of Ship Research,1988,32(4):246-262.
[8] Hirt C W, Nichol B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. J. Comp. Phys.,1981,39:201-221.
[9] 李谊乐,刘应中.二阶精度的VOF自由面追踪方法及其应用[J].船舶力学,1999,3(1):44-52.
[10] 万鹏程,傅慧萍.舰船气泡尾流数值模拟[J].上海交通大学学报,2013,47(2):193-202.
[11] 张振江,陈作钢.船舶CFD结构化网格自动生成技术的开发[J].上海交通大学学报,2012,46(2):317-322.
A Method of Ship Flow Field Numerical Calculation
ZHANG Yongkun WANG Shule
(No. 91439 Troops of PLA, Dalian 116041)
The influence of grid division and turbulent model to resistance, wave ship and precision of flow prediction has been investigated by selecting ship model DTMB5415 as calculated object and using RANS method and VOF model. First, coarseness, middle and huge grid division have been designed to calculate wave flow field. By comparing resistance and wave ship date of the test with calculating data, the results show that middle count grid divisions can obtain veracity of calculate results and higher calculate efficiency. Second, three turbulent flow models have been used to compute total resistance and ship wave. The SST k-ω turbulent flow model can satisfy calculated results accuracy under high calculate rate. Finally, middle grid division and SST k-ω turbulent flow model have been selected to calculated ship wave. The results showed that the calculated results have been agreed with the experiment data.
flow field, computational grid, VOF method, numerical calculation
2015年4月12日,
2015年5月27日
张永坤,男,博士,工程师,研究方向:水下爆炸。
U661.2
10.3969/j.issn.1672-9730.2015.10.040

