半悬挂舵的敞水水动力性能与舵力预估方法研究*

林友红

(海军工程大学舰船综合试验训练中心 武汉 430033)



半悬挂舵的敞水水动力性能与舵力预估方法研究*

林友红

(海军工程大学舰船综合试验训练中心 武汉 430033)

基于RANS方程结合RNGk-ε湍流模型,论文针对某半悬挂舵的敞水水动力性能进行了数值预报,并与相同轮廓的梯形舵进行了对比分析。结果表明:不同舵角下半悬挂舵的挂舵臂升力约为舵叶升力的20%,挂舵臂阻力基本不随舵角变化;相同迎流速度下半悬挂舵的失速角较梯形舵大,在舵未失速时梯形舵舵叶升力系数要大于半悬挂舵舵叶的升力系数,而两者的阻力系数相当;同等来流条件下,半悬挂舵的舵叶压力中心较梯形舵后移距离约为舵底弦长的17%;采用等弦长法可较为准确地预估半悬挂舵的总升力与总阻力,半悬挂舵舵叶对舵杆的扭矩则可通过舵叶简化法得到较为合理的取值。

半悬挂舵; 水动力性能; CFD; 预估方法

Class Number U664.36

1 引言

操纵性是船舶重要航行性能之一,船舶的操纵运动主要依靠操舵来完成,有关舵的水动力性能参数既是船舶操纵性计算不可缺少的输入条件,也是舵机选型和舵杆设计的重要依据。随着船舶吨位及舵尺寸的不断增大,半悬挂舵的应用越来越广泛,在以往工程计算中矩形舵和梯形舵的舵力预估有大量试验资料[1～2]和经验公式[3]可供参考,然而关于半悬挂舵水动力性能的试验研究资料却相当有限。早期藤井齐等[4]通过自航模型试验比较分析了相同面积梯形舵与半悬挂舵的操纵性能,结果表明梯形舵的操纵效果明显优于半悬挂舵;周昭明等[5]拟合了不同展弦比敞水半悬挂舵与矩形舵的法向力系数,获得了适用于特定条件下的半悬挂舵法向力预估方法,并通过自航模试验较为详尽地比较了相同舵叶面积的半悬挂舵与矩形舵两种舵型的操纵效果;文献[6]中采用平均宽度法对敞水下半悬挂舵的舵力进行预估但并未开展可行性的数值验证。近年来所发表的公开资料中关于半悬挂舵水动力性能的系统分析较为少见,半悬挂舵与轮廓相同的梯形舵周围流场有何差异及如何应用已有矩形舵、梯形舵的相关资料来预估半悬挂舵水动力性能还待更深入的研究。

随着计算机性能的不断提高和CFD技术的日趋成熟,采用商用软件来预报船舵水动力已取得了一定的进展。Karim & Ahmmed[7]和Gim & Lee[8]的研究结果表明基于RANS方程结合现有湍流模型能够较为准确地获得小展弦比舵周围的流场细节信息,Choi等[9]则对半悬挂舵挂舵臂与舵叶缝隙间的空化腐蚀性能进行了数值研究并取得较为满意的结果。然而对于不同舵角下半悬挂舵的挂舵臂对舵叶水动力性能有何影响还未见开展相关研究。由于挂舵臂与舵叶之间存在一定的微小缝隙,物理建模和网格离散过程都较为复杂,在舵的设计过程中如果预选方案较多会使工作量和工作周期大大增加,不利于不同舵方案的性能对比也不利于舵杆位置的快速优化,因此探讨快速预报舵水动力性能的简化方法尤为重要。

本文应用Fluent商用软件基于RANS方程结合RNGk-ε湍流模式,对敞水半悬挂舵的水动力性能及舵周围流场进行了分析,对比了相同轮廓的梯形舵与半悬挂舵水动力性能的差异,并对半悬挂舵舵力和扭矩的预估方法进行了探讨,本文结论可为半悬挂舵的设计及船舶操纵性计算提供一定参考。

2 数学模型

2.1 基本方程及湍流模型

RANS方程是粘性流体运动学和动力学的控制方程,本文以它作为求解三维粘性流场的基本方程,其具体数学形式如下:

(1)

式中:ρ为流体密度,μ为流体粘度,p为静压,fi为单位质量的质量力,ui、uj为速度分量。数值计算时选取RNGk-ε湍流模型[10]及非定常方式进行迭代求解,时间步长取为0.0001s。

2.2 计算对象及网格划分

如图1所示,半悬挂舵包括可动舵叶、挂舵臂及与船体连接部分。由于半悬挂舵几何形状较为复杂,针对舵进行结构化网格划分相当困难,因此对舵周围空间进行非结构化网格离散,同时为确保数值预报的准确度在舵近壁面处生成15层的细化网格。本文所研究的半悬挂舵主参数详见表1。

图1 半悬挂舵的主要组成部分

舵剖面舵叶面积(m2)挂舵臂面积(m2)连接部分面积(m2)舵叶展弦比平衡系数NACA00180．02860．00760．00881．620．286

2.3 计算流域设置

为有效减小数值计算量,本文采用结构-非结构的混合网格进行计算,即在舵周围进行非结构网格离散而对远场采用结构化网格划分方式,内部流域的非结构网格总数为210万,远场流域的结构网格总数为300万,非结构网格与结构网格之间的交接面设置为interface进行数据传递。图2给出了计算流域的大小及边界条件的设置情况,具体如下:

图2 计算流域及边界条件设置

1) 流域的入口距离半悬挂舵的导边约5倍平均弦长,其边界条件设置为速度入口;

2) 流域的出口距离半悬挂舵的随边约15倍平均弦长,其边界条件设置为压力出口,压力初值为未扰动时的边界压力值;

3) 流域的左右边界距半悬挂舵的纵向中心线约5倍平均弦长,上下边界距舵中心约8倍弦长,其边界条件设置为无滑移且不可穿透的边界条件;

4) 内部流域为正六面体形,其长度取舵平均弦长的1.8倍,高度取舵高的1.4倍,流域宽度取舵最大厚度的4倍;

5) 在半悬挂舵的表面定义为无滑移且不可穿透的边界条件。

2.4 相关符号及无因次量定义

这里半悬挂舵的阻力系数Cd、升力系数Cl、舵杆扭矩系数M′、压力中心系数l′和升阻比τ的定义式如下:

(2)

式中:R为舵的阻力(N),L为舵的升力(N),M为舵杆所受扭矩(N·m),ρ表示水的密度(kg/m3),S为舵在中纵剖面上的投影面积(m2),v为来流速度(m/s),b为舵底剖面弦长,l为水动力合力作用点离舵底前缘的距离(m)。

3 半悬挂舵水动力性能研究

3.1 半悬挂舵的水动力分析

为分析半悬挂舵不同部位处的受力规律,开展了迎流速度v=2.597m/s不同舵角下半悬挂舵的水动力计算,计算结果如图3和图4所示。由图可知:舵与船体连接部分的升力和阻力均较小且不随舵角变化而变化,舵叶所受升力与阻力在未失速的情况下与舵角成线性关系,尽管挂舵臂纵向中心线始终与来流方向平行,在不同舵角下其所受升力约为舵叶升力的20%,挂舵臂所受阻力则基本不随舵角变化。

图3 不同舵角下舵叶、挂舵臂及连接部分的升力对比

图4 不同舵角下舵叶、挂舵臂及连接部分的阻力对比

与矩形舵类似,在不同舵角下半悬挂舵叶面侧水流的流速较舵叶背侧水流流速小,进而造成了舵面的两侧存在一定的压力差。由图5可知,在不同舵角下挂舵臂的背流面与迎流面存在压差,且随着舵角的增大压差逐渐增大,两侧压差施加在挂舵臂上形成与舵叶升力方向相同的横向力。

图5 典型舵角下挂舵臂叶背叶面的压力分布图

为更为直观地了解半悬挂舵的周围流场信息,选取舵角δ=10°、15°、25°、35°时舵叶背侧的流场进行分析。由图6可知,在10°舵角下挂舵臂后的舵叶周围已经产生较为严重的回流现象,导致该现象的原因是由于舵两侧的压差使得舵与挂舵臂的缝隙间存在叶面流向叶背的绕流,该绕流与叶背侧近舵表面水流形成一定的速度间断面,因此即使在小舵角下挂舵臂所遮挡的翼段会形成较为强烈的回流涡现象,回流涡的存在必然使得此段翼型升力性能大大减小。另外,相比于挂舵臂后的舵叶,挂舵臂以下的舵叶由于展弦比较小,在舵角δ=35°时才出现较为强烈的回流涡,由于此段舵叶面积要远大于挂舵臂后舵叶面积,因此整体失速角出现在30°以后。

3.2 半悬挂舵与梯形舵的对比分析

为分析半悬挂舵与梯形舵的水动力性能差异,本文对与该半悬挂舵轮廓相同的梯形舵进行了数值计算,梯形舵包括船体连接部分与可动舵叶,与半悬挂舵不同的是二者的可动舵叶面积不同,梯形舵的网格划分形式与计算模型均与半悬挂舵相同。图7给出了梯形舵的三维模型及网格划分情况。

图6 典型舵角下半悬挂舵的周围流场信息

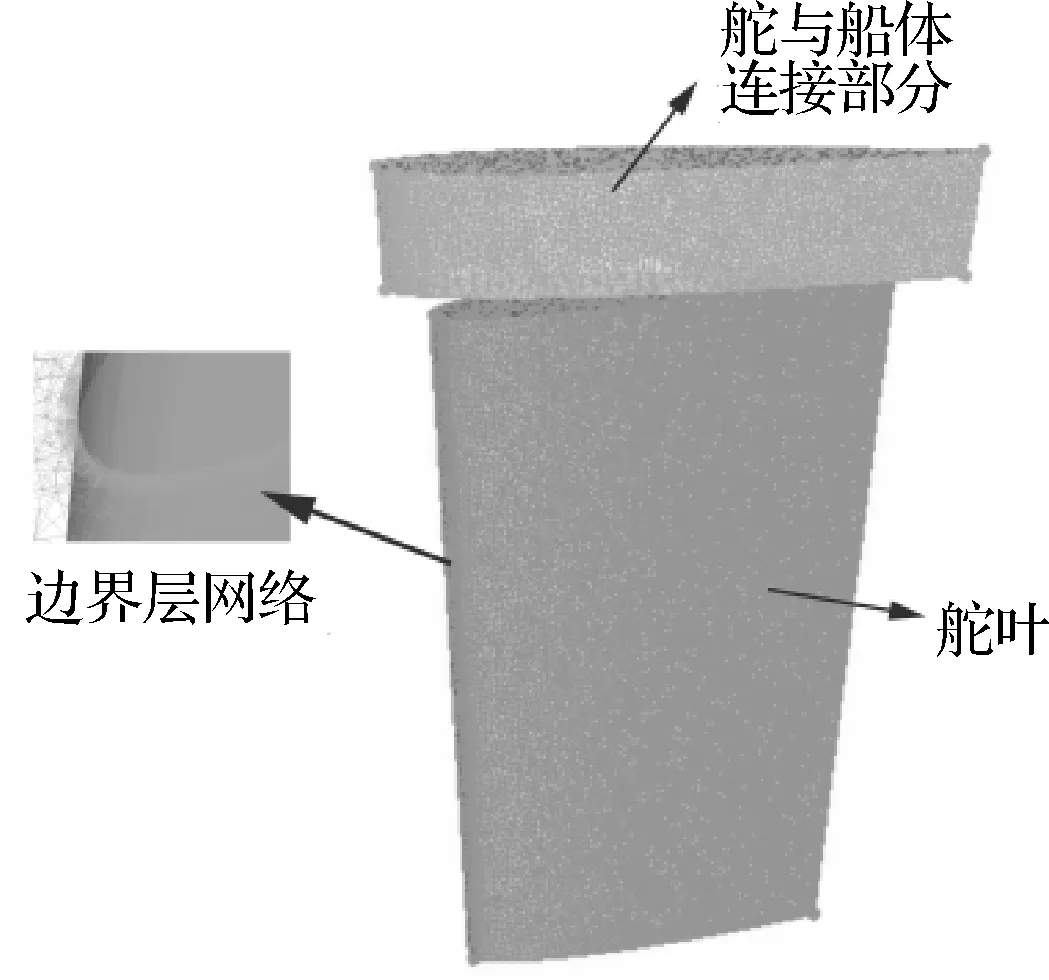
图7 梯形舵的三维模型及网格划分

图8为半悬挂舵与梯形舵舵叶的升阻系数计算结果。分析可知,梯形舵的失速角约为18°,远小于半悬挂舵的失速角,其主要原因是梯形舵的展弦比要大于半悬挂舵的实际展弦比。在梯形舵未失速时,梯形舵舵叶的升力系数要大于半悬挂舵舵叶的升力系数,而两者的阻力系数相当。另外舵的升阻比是评判舵水动力性能的重要参数,由梯形舵与半悬挂舵舵叶在不同舵角下的升阻比(见图9)可知,两舵均未失速(即舵角δ<18°)工况时,梯形舵的升阻比约为半悬挂舵的1.5倍。

图10给出了两舵在未失速情况下的扭矩系数对比图。分析可知,半悬挂舵的扭矩系数仅为梯形舵的约1/4,两者扭矩差别较大的原因是半悬挂舵与梯形舵的压力中心距舵杆的位置存在较大差异;在现有舵杆位置下两种舵型的压力中心大都位于舵杆之前,并随着舵角的增大压力中心往随边移动。另外,半悬挂舵的压力中心系数约为梯形舵的2.3倍(见图11),即半悬挂舵的压力中心较梯形舵后移舵底弦长的17%左右。

图8 半悬挂舵与梯形舵总升阻系数的对比

图9 半悬挂舵与梯形舵舵叶升阻比的对比

图10 半悬挂舵与梯形舵扭矩系数的对比

图11 半悬挂舵与梯形舵压力中心系数的对比

4 舵力预估方法研究

4.1 方法介绍

为快速简便地预估半悬挂舵的水动力性能,本文基于可动舵叶面积不变的原则采用三种简化方法对半悬挂舵进行简化,具体方法如下:

简化方法1:保持舵高、随边及舵杆位置不变,将导边平行内移(图12),称为等展长简化法;

简化方法2:保持随边、导边、舵杆位置及舵底边弦长不变,将舵顶端弦长平行下一(图13),称为等弦长简化法;

图12 等展长简化法

图13 等弦长简化法

简化方法3:忽略挂舵臂整流效应的影响,只针对舵叶进行计算(图14),称为舵叶简化法。

图14 舵叶简化法

4.2 结果与分析

如图15～图17所示,通过将简化方法所获得的升力、阻力及舵叶对舵杆的扭矩与半悬挂舵舵叶与挂舵臂的总阻力、总升力及舵叶对舵杆的扭矩对比可知,采用等弦长简化法所得升力、阻力计算结果与实际半悬挂舵的计算结果吻合较好,而采用舵叶简化法可得到相对合理的舵杆扭矩结果。

图15 不同方法的升力计算结果对比

由于等展长简化法模型的展弦比实际半悬挂舵的展弦比要大,因此相同舵角下升力较实际半悬挂舵模型的要大,但由于其压力分布与实际舵模型存在较大差异,使得等展长比简化法所预报的舵杆扭矩误差较大。等弦长简化法实际将半悬挂舵的舵叶上下两部分进行了整合,其展弦比更接近于实际半悬挂舵的展弦比,因此等弦长简化法所得到的升力和阻力误差较小,但由于梯形舵的压力中心较为靠前,因此等弦长简化法计算的舵杆扭矩要远大于实际半悬挂舵的舵杆扭矩。

图16 不同方法的阻力计算结果对比

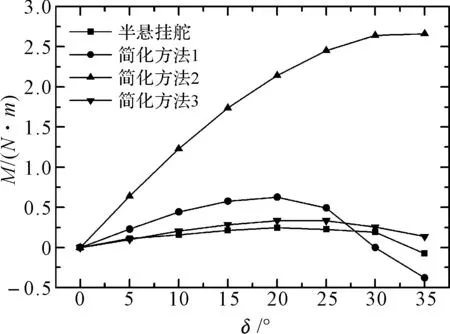
图17 不同方法的扭矩计算结果对比

图18 半悬挂舵舵叶的叶面压力分布(δ=25°)

图19 舵叶简化法的叶面压力分布(δ=25°)

图20 半悬挂舵舵叶的叶背压力分布(δ=25°)

图21 舵叶简化法的叶面压力分布(δ=25°)

图18～图21为实际半悬挂舵与舵叶简化法在舵角δ=25°时的叶背叶面压力分布。分析可知,采用舵叶简化法进行数值计算时,由于没有挂舵臂的遮挡效应,挂舵臂后的舵叶导边压力分布与实际半悬挂舵存在一定的差异,但其总体压力分布较其他简化方法与实际半悬挂舵更为吻合,因此采用舵叶简化法来预估的舵叶升力和舵杆扭矩误差较为合理。

5 结语

基于RANS方程结合RNGk-ε湍流模式,本文对敞水条件下半悬挂舵与梯形舵的水动力性能及舵周围流场进行了分析,获得的主要结论如下:

1) 不同舵角下,半悬挂舵的挂舵臂升力约为舵叶升力的20%左右,而挂舵臂的阻力基本不随舵角变化而变化;

2) 相同迎流速度下,半悬挂舵的失速角大于梯形舵,在舵未失速时梯形舵的舵叶升力系数要大于半悬挂舵舵叶的升力系数,而两者的阻力系数相当,相同舵角下半悬挂舵的舵叶压力中心较梯形舵后移距离约为舵底弦长的17%;

3) 采用等弦长法可较为准确地预估半悬挂舵的总升力与总阻力,半悬挂舵舵叶对舵杆的扭矩则可通过舵叶简化法得到较为合理的取值。

[1] Hisayoshi T, Tomokazu O, Norihiro M, et al. Experimental study on rudder performance[J]. Journal of the Kansai Society of Naval Architecs,1975,159:19-27.

[2] Shojiro O. Investigation on the effect of propeller race upon the performance of rudders[J]. Journal of Society of Naval Architects of Japan,1959,104:29-38.

[3] 冯崇谦.船用襟翼舵[M].北京:国防工业出版社,1989:86-121.

[4] Hitoshi F. Experimental researches on rudder performance[J]. Journal of Society of Naval Architects of Japan,1960,107:105-111.

[5] 周昭明.单桨船两种舵型的舵力和操纵效果的比较试验[J].船舶工程,1981,3:10-18.

[6] 梅琴生.船用舵[M].北京:人民交通出版社,1981:53-68.

[7] Karim M M, Ahmmed M S. Numerical study of periodic cavitating flow around NACA0012 hydrofoil[J]. Ocean Engineering,2012,55:81-87.

[8] Gim O S, Lee G W. Flow characteristics and tip vortex formation around a NACA 0018 foil with an endplate[J]. Ocean Engineering,2013,60:28-38.

[9] Choi J E, Kim J H, Lee H G. Computational investigation of cavitation on a semi-spade rudder[J]. Journal of Marine Science and Technology,2010,15(1):64-77.

[10] 张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005:105-169.

[11] 陆惠生,朱文蔚,费乃振,等.敞水舵的试验研究[J].上海交通大学学报,1981,2:15-37.

Study on the Hydrodynamic Performance and Force Estimation Method for the Semi-spade Rudder

LIN Youhong

(Center of Comprehensive Testing and Training for Naval Ships, Naval University of Engineering, Wuhan 430033)

Based on the RANS equation and RNGk-εturbulent model, the hydrodynamic performance of a semi-spade rudder is numerically investigated in present paper. The hydrodynamic force of a similar trapezium rudder is also calculated by the same numerical model. Result shows that the lift force exerted on the rudder horn is about 20% of the rudder blade’s lift force at different attack angles, but the resistance of rudder horn varies slightly with the attack angle. Before the stall happens, the lift coefficient of semi-spade rudder’s blade is smaller than that of trapezium rudder while the semi-spade rudder’s stall angle is much larger than that of trapezium rudder under the same flow rate. Compared with the trapezium rudder, pressure center of the semi-spade rudder’s blade moves backwards about 17% of the chord length at rudder bottom. For the semi-spade rudder, the lift and resistance can be estimated relatively accurately by the equal-chord simplification and the torque at the main piece exerted by the rudder’s blade be predicted reasonably by the blade simplification.

semi-spade rudder, hydrodynamic performance, CFD, estimation method

2015年4月7日,

2015年5月27日

林友红,男,硕士,工程师,研究方向:舰船综合试验技术。

U664.36

10.3969/j.issn.1672-9730.2015.10.037