人工蜂群算法的性能比较研究

王 慧

（河北工程技术高等专科学校，河北省沧州市浮阳南大道6号 061001）

人工蜂群算法（artificial bee col ony al gorit h m，ABC）是最近提出的一种用于连续数值优化问题的新型群集智能方法，该算法结构简单易于实现，其中的差分搜索算子具有自适应收敛性质。

蜜蜂采蜜群集智能模型包含三个主要部分：蜜源，采蜜蜂和未采蜜蜂［1］。蜜蜂是通过舞蹈语言与种群内的同伙进行联络的，并将食物的来源、性质、方位（方向）和距离等通知伙伴。蜜蜂关于食物源信息的交流发生在舞蹈区，相应的舞蹈称为摆尾舞［2］。观察蜂可以通过观察采蜜蜂的舞蹈来了解关于食物源的信息，并选择一个蜜源进行采蜜活动。由于更好的蜜源有更多的信息传递，所以观察蜂将会以更大的概率选择更好的蜜源。采蜜蜂按照与蜜源收益率成正比的概率，通过摆尾舞共享它们的信息，并且它们的舞蹈会持续一段时间。因此，采蜜蜂征募观察蜂的个数和食物源的收益率成正比。

1 人工蜂群算法原理与实现

在ABC算法中人工蜂群包含三个组成部分：采蜜蜂、观察蜂和侦察蜂。群体的一半由采蜜蜂构成，另一半由观察蜂构成。每一处蜜源仅有一个采蜜蜂，也就是说蜜源数和采蜜蜂数目相等，放弃所采蜜源的采蜜蜂成为侦察蜂。人工蜂的搜索活动可以概括如下：采蜜蜂根据它们记忆中的蜜源位置在其邻域内确定另一个蜜源；采蜜蜂在蜂巢内将它们的信息通过舞蹈共享给观察蜂，观察蜂选择一个蜜源；观察蜂根据所选择的蜜源在其邻域内搜索另一个蜜源；放弃所采蜜源的采蜜蜂将成为侦察蜂并搜索一个新的随机蜜源。

在ABC算法中，每个蜜源的位置代表优化问题的一个可能解，蜜源的花蜜量对应于相应解的质量或适应度。首先，ABC随机产生初始群体即ne个初始解，ne为采蜜蜂数，也等于蜜源数目，每个解xi（i＝1，2，…，ne）是一个d维的向量，d为优化参数的个数。以这些初始解为基础，采蜜蜂、观察蜂和侦察蜂开始进行循环搜索。采蜜蜂根据它记忆中的局部信息产生一个变化的位置并评价新位置的花蜜量，如果新位置优于原位置，则该蜜蜂记住新位置并忘记原位置。所有的采蜜蜂完成搜索过程后，它们将所知道的蜜源信息通过舞蹈区与观察蜂共享。观察蜂根据从采蜜蜂处得到的信息，按照与花蜜量相关的概率选择一个蜜源位置，并像采蜜蜂那样对记忆中的位置做一定的改变，并评价新候选位置的花蜜量，若新位置优于记忆中的位置，则用新位置替换原来的蜜源位置；否则保留原位置。换句话说，贪婪选择机制被用于选择原位置和新的候选位置。

为了使算法适用于最小化问题，采用基于排序的适应度分配［3］。排序方法引入种群均匀尺度，提供了控制选择压力的简单有效的方法。一个观察蜂选择某个蜜源的概率为

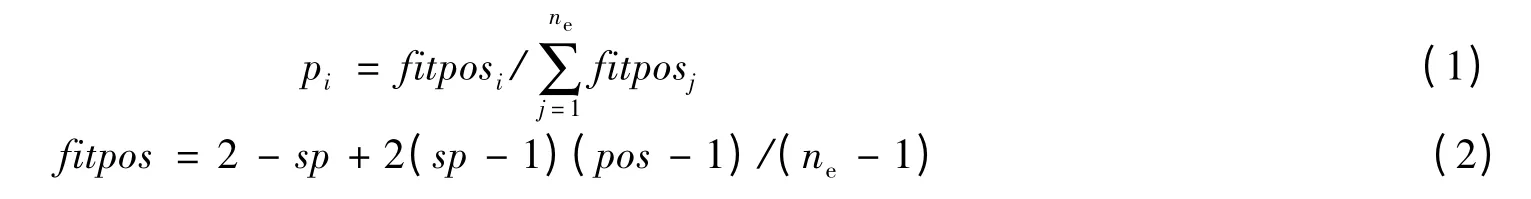
式中:pos为个体在种群中的序位;sp为选择压力;fitpos为基于排序的适应度。为了根据记忆位置产生一个新位置，ABC采用下式

式中:k∈{1，2，…，ne}、j∈{1，2，…，d}是随机选择的下标，且满足k≠i;∅为参数，称为搜索因子，是在［-1，1］范围内的随机数，它控制了xij邻域内新解的产生并代表蜜蜂对两个可视范围内蜜源位置的比较。从式(3)可以看出，随着参数xij与参数xkj之间差距的缩小，对位置xij的扰动也越来越小，因此随着对最优解的逼近，步长会自适应的缩减，使得算法具有自适应收敛特性。

假如蜜源xi经过限定的探测次数lc之后，不能够被改进，那么该位置将被放弃，该位置的采蜜蜂成为侦察蜂，侦察蜂在搜索空间内随机选择一个蜜源位置替换xi，其操作如下

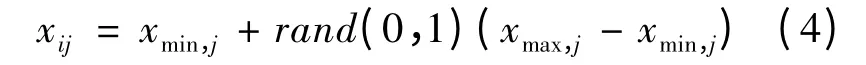
ABC算法流程如图1所示。

2 算法性能比较分析

采用如下4个基准测试函数对算法进行优化测试:

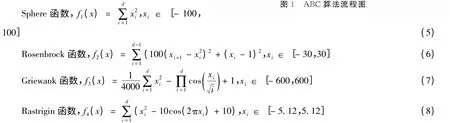
式中:d为变量维数，取d=30;函数f1(x)是单峰函数;函数f2(x)是很难极小化的病态函数;函数f3(x)，f4(x)都是具有大量局部最优点的多峰函数。4个基准测试函数的全局极小值均为min fi(x)=0，(i=1，2，3，4)。

为验证ABC算法的优化性能，将其与常用的几种全局优化算法RCGA，PSO，DE进行了比较。算法的参数设置如下:公共参数为群体规模N=50，迭代次数tmax=2000，基于排序的适应度变换中选择压力sp=1.5;RCGA中采用算术交叉、非一致变异算子［4］、基于排序的适应度变换以及精英保留策略，交叉概率pc=0.8，变异概率pm=0.02，非一致变异算子控制参数b=5;PSO算法中采用带有惯性权重的PSO算法，惯性权系数w从0.9线性递减到0.4，加速常数c1=c2=2.0，粒子最大速度限定为搜索空间的一半［5］;DE算法中采用标准DE算法［6］，即DE/rand/1/bin，变异因子F=0.5，交叉因子Cr=0.9［7］;ABC算法中采蜜蜂和观察蜂个数(n0)均为群体规模的一半，即ne=n0=N/2，采用基于排序的适应度变换，采蜜蜂转变为侦察蜂的限制搜索次数取为lc=ne×d［8］。可以看出ABC除了公共参数，需要调整的算法参数较少，仅有一个变化的参数lc。

将上述4种不同算法对4个基准测试函数分别独立运行50次后将最优解取平均值，并计算最优化结果的标准差，结果如表1所示。可以看出ABC算法除了f3优化结果比DE算法稍差外，其他函数优化结果均优于其他几种算法。

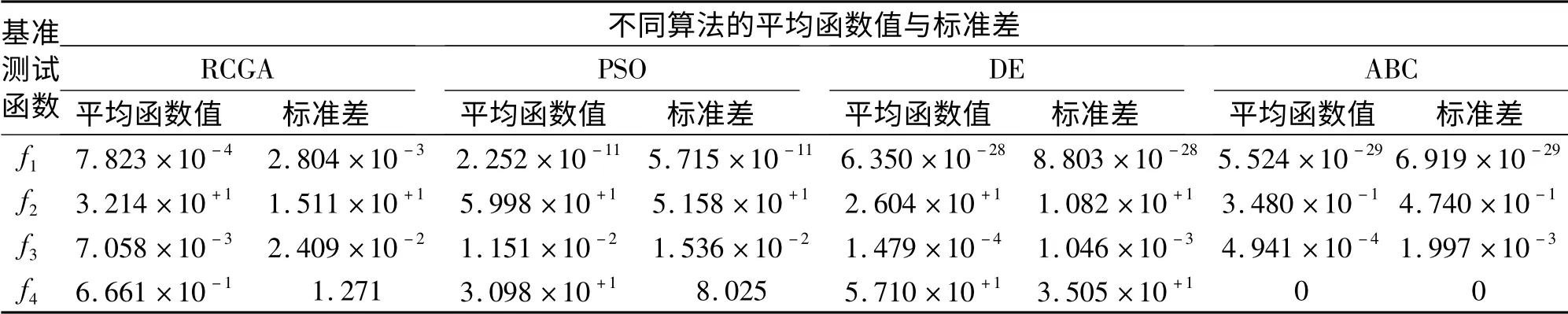
表1 四种算法独立运行50次平均最优值比较

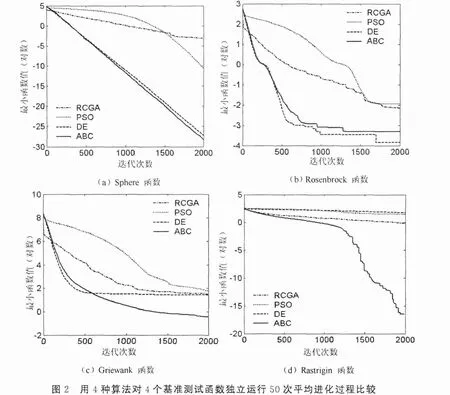
图2为采用RCGA，PSO，DE和ABC对4个基准测试函数独立运行50次，平均最小函数值随迭代次数的变化过程曲线。由图2可以看出，ABC算法和其他几种算法相比不但具有很强的全局搜索能力，而且具有较快的收敛速度，其优化性能大大优于同类的PSO算法。

3 结论与展望

ABC算法是受蜜蜂采蜜行为启发提出的一种新型群集智能优化算法，具有结构简单、控制参数少、全局搜索能力强、搜索速度快以及具有自适应收敛性质等优点，被广泛应用于图像处理、数据聚类、蛋白质检测、动态路径选择、可靠性冗余分配问题等，均取得了良好的应用效果。但人工蜂群算法的研究仍处于初级阶段，有很多问题需要进一步研究和解决，如理论分析、生物学基础、算法的改进、与其他算法的融合、算法的工程应用等。

［1］ Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony(ABC)algorithm［J］.Journal of Global Optimization，2007，39(3):459-471.

［2］ Seeley T D.The Wisdom of the hive［M］.Cambridge，MA:Harvard University Press，1995.

［3］ 王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安:西安交通大学出版社，2002.

［4］ Kaelo P，Ali M M.Integrated crossover rules in real coded genetic algorithms［J］.European Journal of Operational Research，2007，176(1):60-76.

［5］ Niu B，Zhu Y L，He X X.MCPSO:A multi-swarm cooperative particle swarm optimizer［J］.Applied Mathematics and Computation，2007，185(2):1050-1062.

［6］ Storn R，Price K.Differential evolution-a simple and efficientheuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11(4):341-359.

［7］ Rahnamayan S，Tizhoosh H R，Salama M M.Opposition-based differential evolution［J］.IEEE Transactions on Evolutionary Computation，2008，12(1):64-79.

［8］ Fei K，Li J，Xu，Q.Structural inverse analysis by hybrid simplex artificial bee colony algorithms［J］.Computers and Structures，2009，87(13-14):861-870.