高长径比气液固三相内环流反应器的流体动力学

王 宇

（抚顺矿务局职工工学院，辽宁抚顺113008）

当前开发煤加氢液化反应器的一个热点是研究采用内环流三相反应器。内环流反应器是一类高效的气-液、气-液-固多相反应器[1]。目前，对于气液固三相内环流反应器的研究大多是轻颗粒的研究[2,3]，且粒径均＞1.5mm，而对于细颗粒（＜1.2mm）的研究很少。鉴于煤液化工艺必须是将煤炭破碎，且煤浆中的煤在反应器内在高温高压下进行加氢反应，应用普通的环流反应器进行该类反应能有效地防止固定床层内的飞温，但不能解决高压操作所导致的反应器外径大、器壁过厚、占地面积大、不易工业化等问题。因此，采用较高长径比的内环流反应器，以空气-水-石英砂为物系，石英砂具有较大的密度和较小的粒径，考察了上升区固含率和循环液速随表观气速的变化规律。

循环液速的预测对环流反应器的设计有至关重要的作用，故结合动量平衡原理推导出三相体系的循环液速模型，并给出其中各局部阻力系数、上升区的气含率和上升区固含率的计算模型。其中，反应器底部换向区的流通面积在很大程度上决定了三相流体在反应器中的循环流动状态，是气液固三相环流反应器设计的关键尺寸，特别对固含率高、固体密度大的体系尤为重要[4]。目前，对该尺寸的设计未有报道，国内外学者对于底部换向区的研究仅限于阻力系数的实验数据拟合[2，5]，或只考虑到上升区与下降区的面积比[5]，并没有考虑到底部换向区的面积和底部换向区的流动状态。因此将底部换向区的流通面积及流动状态与底部换向区的阻力损失系数关联在一起，以达到预测循环液速的目的。

1 实验部分

1.1 实验装置及流程

实验采用的中心气升式内环流反应器的主体由有机玻璃制成，其内径为0.09m，高为2m；导流筒（材料为PVC）内径为0.06m，壁厚为0.0023m，高为1.55m,实验流程见图1。

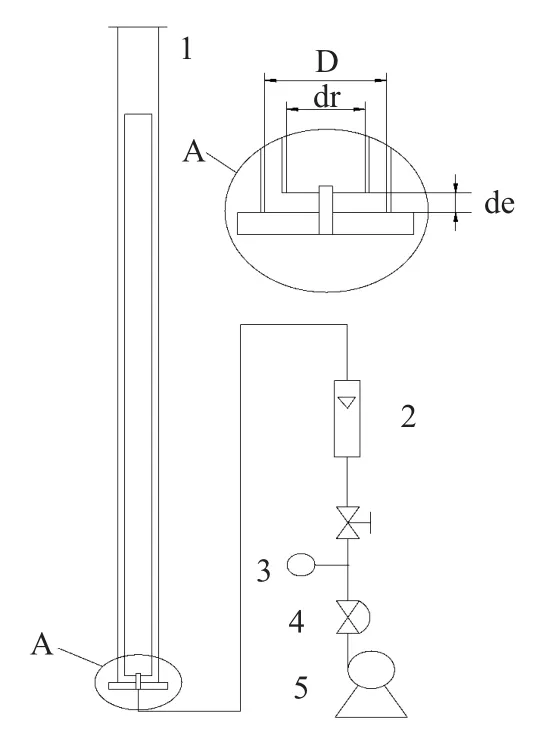
图1 气升式内环流反应器实验装置流程图Fig.1 Schematic flow diagram of experimental unit for internal loop airlift reactor

1.2 实验条件及实验原理

实验在常温常压下进行，三相物系为空气-水-石英砂。实验起始静液高为1.6m，导流筒内部表观气速在0.013～0.045m·s-1。石英砂密度为2650kg·m-3。石英砂粒径分别为（0.1±0.05）mm、（0.2±0.1）mm、和（1.0±0.2）mm 3 种粒径。

气含率和固含率的测量应用压差法和直接取样法测量[8]；采用电导脉冲法测量循环液速[12]。

2 理论分析

根据动量平衡原理，在定态下，气升式内环流反应器的上升区和下降区间的流体静压差是液体循环的推动力，该推动力与流体沿循环回路引起的总摩擦压降相平衡,

在气升式内环流反应器中，总摩擦压降是流体在上升区，下降区，气液分离区和底部换向区流动时的各局部压降之和，

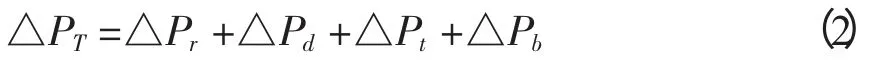
由于颗粒粒径较小，能够均匀的分布在反应器中，故可将三相体系中的固、液两相看成拟均相，各个区域的压降根据范宁公式计算，

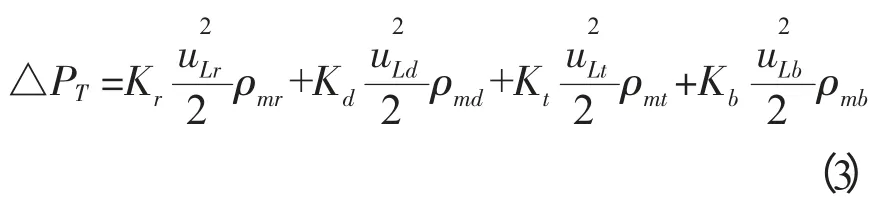
其中，ρmi=εigρg+εisρs+（1-εig-εis）ρt，由于底部换向区的气含率很小，可忽略不计，所以ρmb=εsbρs+（1-εsb）ρt，底部换向区的固含率可看作与下降区的固含率相等；由于气液分离区的阻力系数较其它处较小可忽略不计[6]。

根据连续性方程再联立（2）,（3）式可得到液体循环速度的预测式（4），

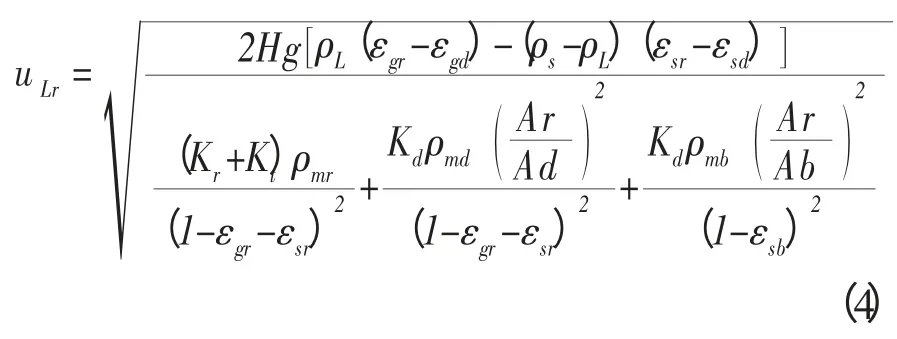
式（4）中，上升区的气含率可根据无因次准数进行关联[2]，但考虑到固体颗粒密度对连续相的影响，用式（5）进行计算，

下降区气含率与上升区气含率呈线性关系[8]，即式（6），

由于上升区的固含率与表观气速、装液高度、固体装载量、固体密度、固体颗粒直径等有较大的关系[5]，因此利用无因次准数进行关联可以得到固含率计算式，

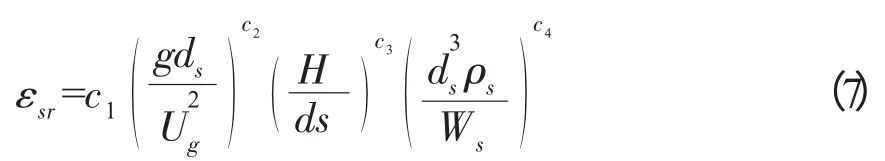
下降区固含率与上升区固含率呈线性关系，即式（8），

由于上升区的阻力损失系数受到气含率、固含率、循环液速、表观气速等的影响，不能将其按单相流处理[7]，故可利用下式计算：

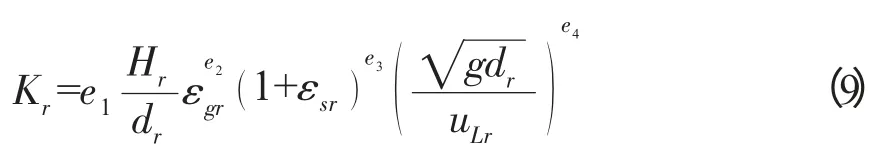
将固、液两相看作拟均相，由于下降区的气含率很低，可按单相流处理[8]。下降区的阻力损失系数可根据Blasius 公式（式（10））计算：

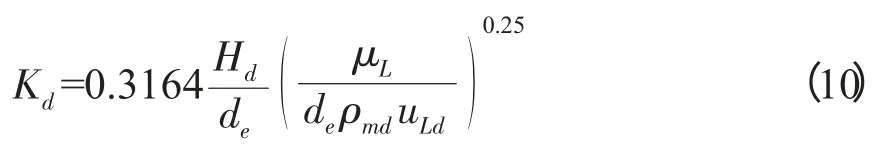
对于底部换向区的研究仅限于阻力系数的实验数据拟合，文献[9]中底部阻力系数仅与下降区和底部换向区的面积之比呈指数关系，但对于三相体系，底部换相区的阻力系数与底部换相区的尺寸和底部换向区的流动状态在很大程度上有关，故可按式（11）进行计算：

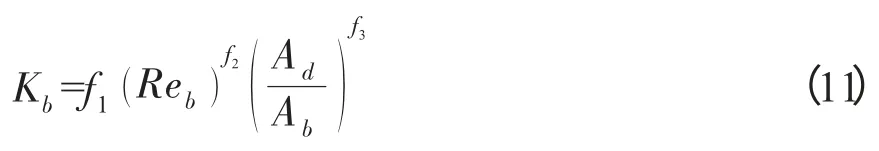
3 结果与讨论

3.1 不同粒径下表观气速对上升区固含率的影响

图2 为固体装载量为0.732kg，颗粒粒径分别为（0.1±0.05）mm、（0.2±0.1）mm、和（1.0±0.2）mm时，底部间隙为0.022m 时，反应器距离分布器0.8m处，上升区固含率随表观气速的变化。

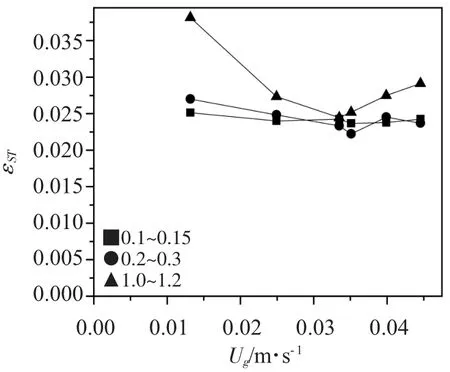
图2 不同粒径下固含率随表观气速的变化Fig.2 Solid holdup in riser and downcomer as a function of superficial gas velocity at different particle size in internal loop airlift reactor

由图2 可知，当ds≤0.3mm 时，固含率随着Ug的增大变化平缓，而当ds＞0.3mm 且Ug≤0.034m·s-1时，固含率随着表观气速的增大而下降；当Ug＞0.034m·s-1时，固含率随着表观气速的增大而上升。这是由于当颗粒粒径过小时，随着Ug的增大，固体颗粒与气泡之间的作用力并不是很明显，而当颗粒粒径较大且Ug≤0.034m·s-1时，由于Ug此时并不是很大，流体处于均匀鼓泡流状态，随着Ug的增加，颗粒的流化床层高度也随着增大，因此固含率下降。但当Ug＞0.034m·s-1时，随着Ug的增加，颗粒的流化床层高度达到最高点后降低，此时循环十分剧烈，可能是固体占据了部分空间，增大了气泡之间发生相互作用的可能性，气泡聚并增大，导致气含率下降，故固含率增大。由图2 还可知，在相同的Ug下，随着颗粒粒径的增大，固含率也随之增大。这是由于在相同气速下，固体粒径越大，气含率越小。而且反应器中气含率、固含率和液含率的总和不变，液含率认为不变，则气含率越小，固含率越大。

3.2 不同粒径下表观气速对上升区循环液速的影响对比图

图3 为颗粒粒径分别为0.1～0.15，0.2～0.3，1.0～1.2mm 时，底部间隙为0.022m 时，反应器距离分布器0.8m 处，上升区循环液速随表观气速的变化与文献[10]中循环液速随表观气速变化的对比图。文献[13]中反应器的长径比为18，玻璃珠直径分别为0.15，0.25，0.35mm。

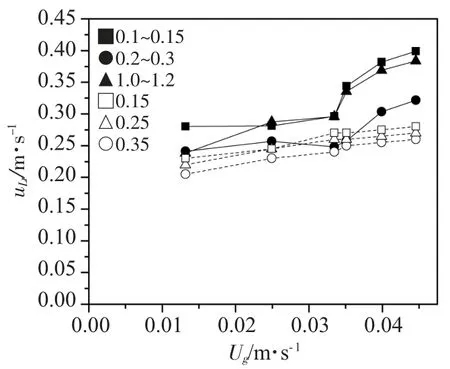
图3 不同粒径下上升区循环液速随表观气速的变化Fig.3 Liquid circulation velocity in riser as a function of superficial gas velocity at different particle size in internal loop airlift reactor

由图3 可知，随着颗料粒径的增大，使得循环液速也随之增大。由图3 还可知，在表观气速固定不变的情况下，循环液速随着固体颗粒粒径的增大而减小，这与王燕[3]等人研究的结果一致。这是因为，随着固体的加入，系统的阻力也随之增加，由于系统的阻力还与固体颗粒的表面积有关，系统中固体的比表面积越大，系统的摩擦阻力也越大[3]。由于作者采用反应器的高径比大于文献[13]中反应器的高径比，故在相同表观气速和相同粒径的条件下，高长径比反应器的循环液速大于低长径比反应器的循环液速，最大时两者相差18.75%。

4 模型计算

4.1 上升区气含率模型的计算

表观气速在0.013～0.045m·s-1下，将实验数据按式（5）、（6）回归得到各经验参数，代入并整理方程可以得到气含率模型式（12）和式（13）。

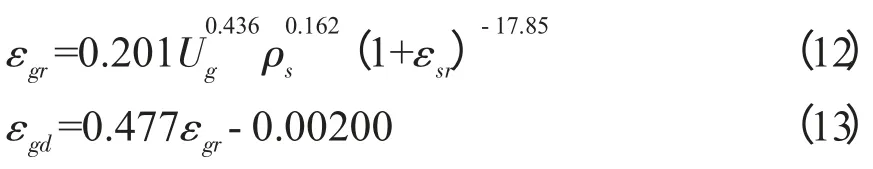
将上升区气含率的实验值与模型计算值进行了比较，上升区气含率的实验值与模型计算值吻合较好，其平均相对误差为6.32%。

4.2 上升区固含率模型的计算

表观气速在0.013～0.045m·s-1下，将实验数据按式（7）、（8）回归得到各经验参数，代入并整理方程可以得到固含率模型式（14）和式（15）。

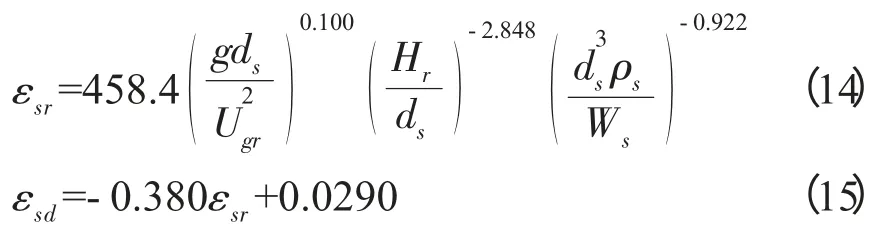
将上升区固含率的实验值与模型计算值进行了比较，上升区固含率的实验值与模型计算值吻合较好，其平均相对误差为4.56%。

4.3 上升区阻力损失系数模型的计算

表观气速在0.0132～0.0446m·s-1下，将实验数据按式（9）回归得到各经验参数，代入并整理方程可以得到上升区阻力系数模型式（16）。

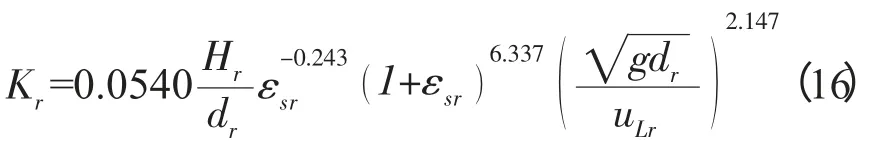
4.4 底部换向区阻力损失系数模型的计算与分析

由于底部换向区的面积和流动状态在很大程度上决定了底部换向区的阻力系数，故将底部换向区的阻力系数与雷诺数和底部换向区的面积联系到一起进行回归分析，底部间隙分别为0.017、0.022、0.03m，将实验数据按式（11）回归得到各经验参数，代入并整理方程可以得到底部换向区阻力系数模型式（17）。

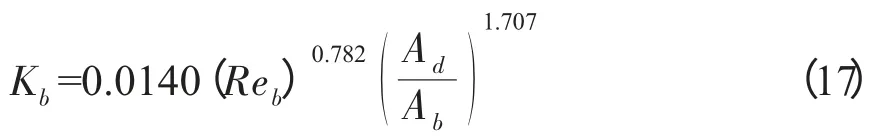
图4 为在3 个不同底部间隙下，底部换向区的阻力系数随雷诺数的变化情况。

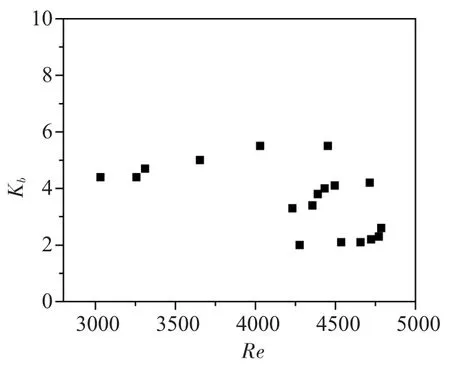
图4 气升式内环流反应器中底部换向区的阻力系数随雷诺数的变化Fig.4 vs a function of in internal loop airlift reactor

由图4 可知，在同一底部间隙下，底部换向区的阻力系数基本保持不变，即不随表观气速的变化而变化，而随着底部间隙的增大，底部换向区的阻力系数变小。

4.5 上升区循环液速模型的计算

将式（10）、式（12）～（17）代入到式（4）中，对该方程迭代求解即可得到循环液速的计算值，将循环液速的实验值与模型计算值进行比较（见图4）可以看出，实验值与计算值吻合较好，其平均相对误差为11.97%。

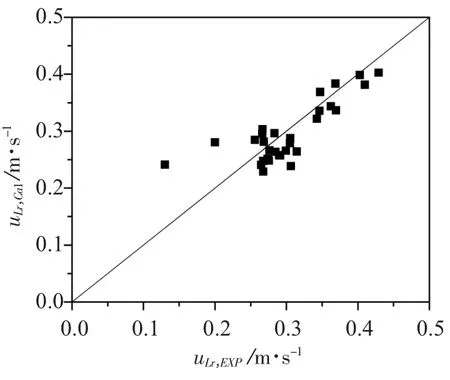
图5 气升式内环流反应器中上升区的循环液速实验值与模型计算值的比较Fig.5 Comparison of experimental and calculated values of liquid circulation velocities in internal loop airlift reactor

5 结论

（1）在鼓泡流下，当ds≤0.3mm 时，上升区固含率随表观气速的增加呈变化平缓趋势，0.3mm＜ds≤1.2mm 时，上升区固含率随表观气速的增加而呈先下降后增加的趋势。

（2）在鼓泡流下，不同粒径下的循环液速均随表观气速的增加而增加，在表观气速固定不变的情况下，循环液速随着固体颗粒粒径的增大而减小，这与王燕[3]等人研究的结果一致。在相同条件下，高长径比反应器的循环液速大于低长径比反应器的循环液速。

（3）根据动量平衡和连续性方程建立了三相物系循环液速模型，模型中关联了气含率、固含率和各个区域的阻力系数。循环液速的模型的实验值与计算值吻合较好，其平均相对误差为11.97%。

（4）底部换向区的阻力系数除了与换向区的面积有关，还与换向区的流动状态有关，从模型方程中可以看出：底部换向区的阻力系数与表观气速的大小无关，只与底部换向区的流通面积和流动状态有关，即底部换向区的面积越大，底部换向区的阻力系数越小，底部换向区的流动越剧烈，底部换向区的阻力系数越小。

符号说明：

A：截面积，m2

Ab：底部换向区面积，Ab=πdrdb，m2

a1，a2，a3，a4：经验参数

b1，b2：经验参数

c1，c2，c3，c4：经验参数

d1，d2：经验参数

e1，e2，e3，e4：经验参数

f1，f2，f3：经验参数

D：反应器内径，m

d：直径，m

g：重力加速度，m·s2

H：静液面高度，m

K：阻力损失系数

△p：压降，Pa

Re：雷诺数，

U：表观速率，m·s-1

u：线速率，m·s-1

W：装载量，kg

希腊字母：

ε：相含率；

μ：黏度，Pa·s-1

ρ：密度，g·cm3

下标：

b：底部换相区

Cal：计算值

d：下降区

EXP：实验值

e：当量

g：气体

i：r 或d 或b

L：液体

m：混合

r：上升区

s：固体

T：总

t：气液分离区

［1］吴春来.煤炭直接液化［M］.北京：化学工业出版社，2010.

［2］孙守华，刘永民，路蒙蒙.GLS-MALR 中的气含率和循环液速［J］.石油学报（石油加工），2011，27（3）：405-410.

［3］王燕，尹侠.固体颗粒对三相气升式环流反应器流动特性的影响［J］.南京工业大学学报，2007,29（5）：101-105.

［4］丁福新，李飞，袁乃驹.环流反应器的发展和应用［J］.石油化工，2004,33（9）：801-807.

［5］朱慧红，刘永民，于大秋.多室气升式环流反应器气、液、固三相相含率的研究［J］.石油学报（石油加工），2004，20（6）：68-73.

［6］刘永民，刘铮，袁乃驹.多管环流反应器的流动和传质特性［J］.化工学报，2001,52（3）：222-226.

［7］AKITA K,OKAZAKI T,KOYAMA H. Gas holdups and friction factors of gas-liquid two-phase flow in an airlift bubble column［J］. Journal of Chemical Engineering of Japan,1998,21（5）:476-482.

［8］刘永民，孙桂大，袁乃驹.多管环流反应器的气含率研究［J］.化学工程，1998,26（2）：23-25.

［9］徐绍莉，刘永民，孙桂大.多管气升式环流反应器的循环液速和气含率［J］.石油化工高等学校学报，2000，13（1）：18-21.

［10］王国胜，王红心.气升式反应器内三相条件下流动行为研究Ⅱ-循环液速的影响［J］.辽宁化工，2001，30（10）：437-439.