磁悬浮开关磁阻电机悬浮系统自抗扰逆系统解耦控制

李雪林，孙玉坤

(1.江苏联合职业技术学院 扬州商务分院，扬州225001;2.江苏大学，镇江212013)

0 引 言

开关磁阻电动机可以在极速、低功耗的条件下运行，但是电机在极速下运行的主要问题是电机的机械轴承容易磨损，机械摩擦会使转子承受很大的摩擦阻力，并且会使电机相关部件发热，发热到一定程度时会使电机气隙变得不再均匀，从而破坏电机的动态特性，电机的效率降低，影响并减少电机及装备的使用年限［1］。为应对此问题，日本电机研究专家展开了磁悬浮开关磁阻电动机(以下简称BSRM)相关技术的探究。BSRM 的特点是没有特殊的机械轴承来支撑转子，而是通过磁悬浮技术将转子运行在稳定的悬浮状态［2-5］，将机械磨损这个电机轴承常见的问题解决了。

电机转子的悬浮保持稳定是BSRM 研究的关键，其中包括悬浮控制的非线性耦合和径向两自由度上的耦合及转矩调节这两方面研究，迄今为止，在轴承径向上的相关解耦研究已有初步的进展［6-8］，但这些研究均设定电机主绕组电流ima为一常数，把转矩设定在运行于理想状态。事实上，转矩动态变化一直在进行，由此，怎样让转矩动态变化时电机ima的摄动对悬浮系统的稳定运行与控制不产生影响，是一个亟待解决的问题。

神经网络系统的优点是非线性逼近能力和容错性，将此应用在对悬浮系统与转矩之间解耦研究中［9］，但神经网络的缺点是训练繁琐复杂。本文对悬浮系统解耦时采用逆系统的简便特点，再利用自抗扰控制器对被控对象数学模型的不依赖特性和优秀的抗干扰能力［10-12］，设计了BSRM 悬浮系统的自抗扰逆系统解耦控制方法。该方法将主绕组电流的摄动视为悬浮系统的外扰，将悬浮系统用逆系统反馈线性化进行解耦，使其成为两个相对独立的子系统，最后采用自抗扰控制器(以下简称ADRC)作为径向位置控制器对复合伪线性系统进行综合，扩张状态器对主绕组电流的摄动进行实时补偿，从而把转矩动态变化对悬浮控制的干扰消除，使悬浮系统稳定运行。该控制策略的有效性和可行性得到了仿真试验验证。

1 磁悬浮开关磁阻电机悬浮系统控制模型

设磁悬浮开关磁阻电机转子的α 方向的径向位置为xα，β 方向的径向位置分别xβ;设ima为主绕组电流;isa1和isa2为 径向力绕组电流。转子的径向力公式如下［6］:

式中:Kf1，Kf2表示系统两个悬浮力系数，由磁悬浮开关磁阻电机实际参数代表，表达式参见文献［6］。

由牛顿第二定律得出转子在径向力方向下的控制模型表达式:

式中:m 为转子质量;mg 为转子所受重力。

把式(1)代入式(2)，径向力控制模型改写:

根据式(3)可知，系统是复杂的有两个输入和两个输出的强耦合系统。

2 磁悬浮开关磁阻电机悬浮系统控制模型的解析逆系统

对于改写的径向力控制模型式(3)，设定状态变量:

且

输入系统变量:

且

输出系统变量:

且从而得出系统的状态方程和输出方程分别为:

利用可逆性对模型进行分析，利用求导对输出方程进行运算，使方程中出现输入变量。再通过式(7)和式(8)推得:

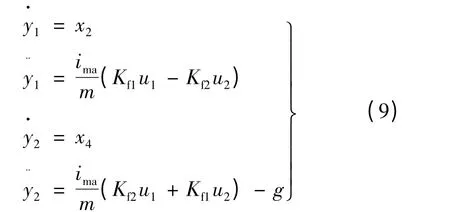
其Jacobi 矩阵:

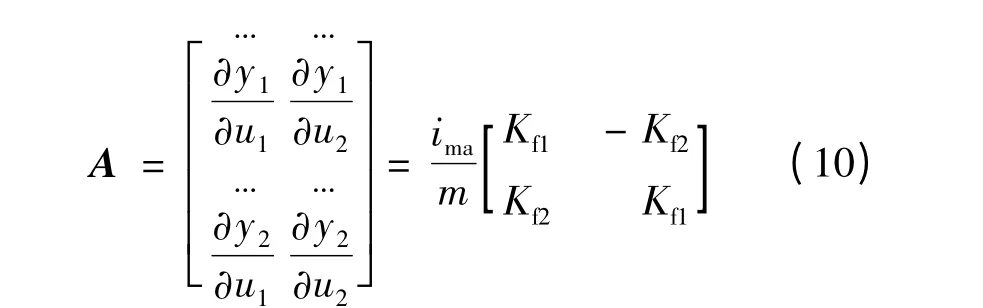
根据rank=2，得出矩阵A 是非奇异矩阵，由阶数α=(2，2)，2 +2 =4，由于系统是4 阶矩阵，从而系统是可逆的。

将逆系统理论的状态反馈线性化方法应用于系统，令:

求解式(11)，得到状态反馈算法:

通过式(12)所表达的系统状态的反馈关系，由磁悬浮开关磁阻电机径向力的控制式(3)可推出无耦合伪线性系统:

3 悬浮系统的ADRC 逆系统解耦控制

3.1 ADRC 的结构及工作原理

自抗扰控制器对被控对象不需要精确的数学模型，对被控对象模型摄动和外界干扰的叠加进行实时估算，并动态补偿的一种非线性控制器，跟踪微分器(TD)和扩张状态观测器(ESO)及非线性状态误差反馈(NLSEF)是自抗扰控制器(ADRC)的三个主要部分。常设定二阶受控系统作示例，图1 为ADRC 的结构［10］。

图1 自抗扰控制器结构框图

跟踪微分器的作用是产生过渡过程然后选出其各阶微分信号，即此过程中y*(t)会产生1 个输出v1(t)和另1 个输出v1(t)的微分信号v2(t)。y*(t)的跟踪信号是v1(t)，这是一个光滑过渡过程。

y(t)对扩张状态观测器产生信号1 z1(t)，信号2 z2(t)，信号3 z3(t)，可以看出y(t)的跟踪信号为信号1 z1(t)，信号1 z1(t)的微分信号为信号2 z2(t)，对系统模型摄动和外界干扰叠加的估算为信号3 z3(t)，对扰动起补偿作用的是z3(t)/b 的反馈。

非线性状态误差反馈利用z1(t)与v1(t)的误差e1(t)及z2(t)与v2(t)的误差e2(t)来产生控制信号u0(t)，u0(t)与z3(t)/b 相减形成最终控制量u(t)。

3.2 ADRC 逆系统解耦控制

由式(13)可以判断，系统经解耦和线性化后，磁悬浮开关磁阻电机悬浮系统在径向上取得了控制的独立性，然而主绕组电流ima产生的干扰却没有有效去除，并且主绕组电流的干扰具有不确定性;另外，外力扰动对悬浮系统控制有无法忽略的影响。所以，对系统悬浮系统采用自抗扰控制来设计控制算法，把主绕组电流ima引起的摄动视为系统的一种外扰，利用ESO 进行实时补偿。由于悬浮系统经逆系统方法反馈线性化为两个相对独立的伪线性子系统，因而把ima引起的摄动影响分为两部分，用w1(ima)和w2(ima)分别表示摄动对两个独立子系统的影响，控制系统结构如图2 所示。

由于径向位置两自由度对称，以x*α自由度为例，给出自抗扰控制器各部分算法如下:

TD 方程:

图2 BSRM 的自抗扰逆系统解耦控制结构图

ESO 方程:

式中:

α1，α2，α3，δ2，bα，bt01，bt02，bt03为可调参数。

NLSEF 方程:

式中:α4，α5，δ3，bt1，bt2为可调参数。

4 仿真试验研究

以磁悬浮开关磁阻电动机实验机为仿真对象，利用仿真软件MATLAB 中Simulink 及模糊逻辑工具箱进行控制系统的解耦仿真试验。实验机各相关参数如表1 所示。

表1 BSRM 参数

4.1 控制系统性能试验和解耦分析

为验证系统的控制性能，对电机转子的起浮过程进行研究，设定转子α 轴径向起始位移为-20 μm，图3 为α 轴径向位移起浮特性图。由仿真分析可知，系统没有超调，动态响应快，调节迅速，显示良好的动态性能。

图3 α 轴径向位移起浮特性图

为进一步检验解耦控制的性能，系统设定不同的时刻进行变化，在初始时刻t=0 时径向α 轴位移给定从-18 μm 变化到0，t=3 ms 时径向β 轴位移给定从0 变化到20 μm，其解耦控制效果由图4(a)和4(b)所示。从而判定一个输出只受一个输入影响，相互没有影响，动态解耦性能非常好。

图4 自抗扰逆系统解耦控制效果

4.2 ima摄动试验

设定磁悬浮开关磁阻电动机主绕组电流ima由5 A 变5.5 A，显然，系统模型将出现较大扰动。图5为ima变化后径向α 轴位移起浮特性图。对比图3可见，在ima发生较大摄动后，径向α 轴位移起浮特性曲线几乎没有变化，从而验证了自抗扰控制器突出的抗干扰特性，说明利用非线性自抗扰控制能够消除数学模型和系统参数的摄动。该试验同时间接验证了自抗扰逆系统解耦控制策略解耦效果不依赖于被控制对象数学模型的特性。

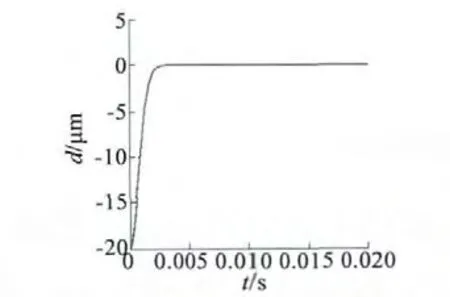
图5 ima变化后径向α 轴位移起浮特性

5 结 语

自抗扰控制器是一种新型的不依赖于被控制对象数学模型的非线性控制器，具有很强的鲁棒性和抗干扰性。结合自抗扰控制和逆系统方法的优点，利用自抗扰控制器来消除系统数学模型和参数的摄动，逆系统方法来进行解耦线性化，设计了BSRM 系统的自抗扰逆系统解耦控制策略。仿真结果验证了该控制策略的有效性。本文研究可知，为了消除逆系统方法依赖于被控制对象精确数学模型的缺点，可以采用一些合适的不依赖于被控制对象数学模型、对模型摄动具有较强适应性的非线性控制器与逆系统方法相结合，对BSRM 系统进行解耦控制。

［1］ 谢宝昌，任永德. 磁悬浮电机及其应用的发展趋势［J］. 微电机，1999，32(6):28 -30.

［2］ 竹本，铃木.改进的无轴承开关磁阻电动机的分析［C］//International Conference IEMD’99，1999:773 -775.

［3］ 竹本，千叶.一种新的无轴承开关磁阻电机采用方波电流控制方法［C］//IEEE 电力工程协会冬季会议，2000(1):375 -380.

［4］ 竹本，千叶.无轴承开关磁阻电机的确定方波电流超前角的方法［J］.IEEE 工业应用，2001，37(6):1702 -1709.

［5］ 竹本，千叶.前馈减振补偿无轴承磁开关磁阻电动机［C］//第七国际研讨会，2000:395 -400.

［6］ 刘羡飞，孙玉坤，磁悬浮开关磁阻电机径向位置解耦及仿真研究［J］.系统仿真学报，2007，19(7):1527 -1530.

［7］ 李雪林，孙玉坤，磁悬浮开关磁阻电机模糊补偿逆系统解耦控制［J］.电机与控制应用，2009(5):16 -20.

［8］ 张 亮，孙玉坤，基于微分几何的磁悬浮开关磁阻电机径向力的变结构控制［J］.中国电机工程学报，2006，26(19):121 -126.

［9］ 孙玉坤，任元.BSRM 悬浮力与旋转力的神经网络逆解耦控制［J］.中国电机工程学报，2008，28(9):81 -85.

［10］ 韩京清. 自抗扰控制器及其应用［J］. 控制与决策，1998，13(1):19 -23.

［11］ 韩京清. 从PID 技术到“自抗扰控制”技术［J］. 控制工程，2002，9(3):13 -18.

［12］ 黄一，张文革.自抗扰控制器的发展［J］. 控制理论与应用.2002，19(4):485 -492.