求解约束优化问题的改进教-学优化算法

李会荣，周亚妮

(1. 商洛学院 数学与计算机应用学院, 陕西 商洛 726000；2. 商洛职业技术学院 公共基础部， 陕西 商洛 726000)

求解约束优化问题的改进教-学优化算法

李会荣1，周亚妮2

(1. 商洛学院 数学与计算机应用学院, 陕西 商洛 726000；2. 商洛职业技术学院 公共基础部， 陕西 商洛 726000)

提出了一种非线性约束优化问题改进的教-学优化算法，该算法首先提出了自适应的教学因子，对学习阶段的迭代方程进行改进，引入了差分变异策略；其次利用约束违反度函数将约束优化问题转化为无约束双目标优化问题，在每次迭代中按照约束违反度的大小保留部分性能较优不可行个体，有效地维持了种群的多样性；最后数值实验表明，该算法具有较快的收敛速度和较好的全局寻优能力.

教-学优化算法； 约束优化； 差分变异； 教学因子

近年来群体智能优化算法作为一种启发式优化算法，得到了迅猛的发展，由于实现简单、收敛速度快、鲁棒性强，而且不需要函数的任何可微、可导等信息，具有良好的适应性，成为优化领域的一个研究热点.目前，具有代表性的群体智能优化算法有：粒子群优化算法[1]、遗传算法[2]、差分进化算法[3,16]和蚁群优化算法[4]等等.2011年Rao R V等人[5-6]提出的一种新型的群体智能优化算法，称为教-学优化算法(TLBO:Teaching-Learning-Based Optimization).教-学优化算法模拟了教师的教学过程和学生的学习过程，目的是通过教师和学生之间的相互学习来提高学习成绩，其参数少、算法简单、速度快、精度高且具有极强的收敛能力，因而一经提出，就引起了国内外很多学者的关注，目前已经应用到一些实际问题，例如无约束优化问题[6]、约束优化问题[7]、多目标优化问题[8]等.

考虑以下一般的非线性约束优化(COP)问题

F={x|gi(x) ≤0,i=1,2…，q;hj(x)=0,j=q+1,…，m}.

非线性约束优化问题广泛存在于科学计算等领域，是一类比较难以解决的优化问题，没有普遍适用的解法.目前在求解约束优化问题的方法主要有确定性的方法和随机性方法2类.确定性的方法主要有罚函数方法、拉格朗日乘子法和可行方向法等，通常往往需要目标函数和约束函数连续，可微等信息，收敛速度较快，但是容易陷入局部极小，且求解的优化问题规模相对较小.近年来，由于进化算法不需要目标函数和约束函数的任何导数信息，同时也是全局优化技术，受到国内外学者的高度重视，已经被应用到各类优化问题中.目前，已经提出了一些融合进化算法的约束处理技术求解约束优化问题[8-11].

本文提出了一种非线性约束优化问题改进的教-学优化算法.该算法对教学因子进行改进，将差分进化算法中的变异思想引入到学习阶段的迭代方程中，有效地保持了种群的多样性，定义了约束违反度函数将约束优化问题转化为无约束双目标优化问题，在每次迭代中按照一定的阈值保持少部分性能较优的不可行个体，有效的维持了种群的多样性.数值实验的结果表明该算法的有效性和通用性.

1　基本教-学优化算法(TLBO)

在教-学优化算法中，学生的人数代表种群的规模，学生学习的科目个数表示优化问题搜索空间的维数，学生学习的结果类似于优化问题的适应度，在整个群体中教师被认为学习的最好者，代表最优解.教-学优化算法的搜索过程分为教学阶段和学习阶段.

1.1教学阶段在教学阶段，利用群体中当前最优个体对其他个体进行教学，有效地融合了群体均值的影响.求解群体每一维的平均值mi，得到平均个体xm=(m1,m2,…，mn)，通过式(1)得到新个体xnew，然后计算其目标函数值，并与旧的个体xold进行比较，如果优于旧的个体，则更新旧个体.

xnew=xold+rand·(xteacher-TF·xm) ,

(1)

其中，xteacher为当前群体中的全局最优个体，即表示教师的知识水平；rand为 [0,1]之间的随机数；TF称为教学因子，表示平均值的变化程度，通常设置为1或2，TF随机地等概率的变化[5]

TF=round[1+rand]，

(2)

其中，round( )表示四舍五入取整.

1.2学习阶段知识水平不仅通过教师的教学而提高，而且还可以通过学生之间的相互影响而提高.所以在学习阶段随机选择2个学习者k,k′，且k≠k′，第i次迭代中由学习者k,k′相互影响而产生新的学习者

(3)

其中， f(xk)与f(xk′)分别表示个体k,k′的目标适应值.如果xnew优于xold，则更新xold，如果xnew优于xteacher，则更新xteacher.

2　约束的处理技术

用教-学优化算法求解约束优化问题时，处理约束条件是关键.笔者采取动态目标的处理方法[12]，其主要思想是将约束违反度函数作为优化的第一个目标，将目标函数作为第二个目标进行优化.为此定义约束违反度函数

(4)

minF(x)=min{φ(x),f(x)} .

(5)

由式(4)可以看出，φ(x)=0的所有解构成了约束优化问题的可行域，因此只有当φ(x)=0时，才开始优化minf(x).但是许多优化问题的最优解就在可行域的边界附近，位于最优解附近的不可行解对于寻找最优解是很有帮助.因此设置一个约束违反度δ≥0，使得φ(x)≤δ时，就开始优化f(x).如果子代个体在可行域的外面，即φ(x)>δ，则此个体以φ(x)为其优化目标，否则此个体以目标函数f(x)进行优化.

如果某个学习者逃离搜索空间，将按式(6)在搜索空间内进行随机赋值.

xnew=xl+rand·(xu-xl)，

(6)

其中，xu,xl分别表示搜索空间的上下界.

3　改进教-学优化算法(ITLBO)

3.1自适应的教学因子在基本的教-学优化算法中，教学因子TF的大小决定着平均值的变化情况，由式(2)可以看出，TF要么取值为1，或者取值为2，即学习者要么从教师那里没有学到知识，要么学习者从教师那里学到全部知识.但是在实际的教学中过程并不是这样，而是介于两者之间.在优化算法中，TF越小则表示搜索的步长较小，收敛速度比较慢；而TF越大则加速算法的收敛速度，但减少算法局部探测能力.为了解决此问题，将TF设置随着迭代次数而自适应变化

(7)

其中，Imax表示最大的迭代次数，t表示当前的迭代次数.从式(7)可以看出，算法开始时教学因子TF取值为2，表示学习者接受知识的能力比较大，有利于加强算法的全局搜索能力，随着迭代进行TF取值为1，最后TF取值为0，表示随着迭代的进行，知识难度的逐渐增加，学习者学习知识的能力开始下降，有利于加强算法的局部搜索能力.

3.2差分变异策略学习者不仅可以从教师那里学到知识，还可以通过教师的引导自己的学习或与其他学习者的讨论而提高学习能力.在基本的教-学优化算法的学习阶段中，新的学习个体只受2个学习者的影响，其实目前最好的学习者(即教师)的影响也不容忽视.因此，受差分进化算法中变异策略DE/best/1思想的启发，将学习阶段迭代方程(3)改进

xnew=xteacher+rand·(xk1-xk2)，

(8)

其中，xk1,xk2为在第i次迭代中2个互异的学习者，若xnew优于xold，则更新xold；若xnew优于xteader，则更新xteacher.

3.3随机变异阶段教-学优化算法与其他智能优化算法一样，容易出现早熟收敛现象，特别是求解高维复杂的优化问题.为此在教-学优化算法中加入随机变异策略，即在每次迭代的中按照一定的变异概率Pm产生如下新的变异个体

xnew=xr1+rand·(xr2-xr3)，

(9)

其中，r1,r2和r3为种群中随机选择的3个互异的个体，若xnew优于xteacher，则更新xteacher.

3.4改进教-学优化算法(ITLBO)的实现步骤

步骤1设置班级学习人数n，学习的科目m，最大迭代次数Imax，初始化的约束违反度δ，设置当前迭代代数t=1；

步骤2在搜索空间中初始化教学优化种群，由式(4)计算初始个体的约束违反度φ(xi),若φ(xi) ≤δ，将第i个个体加入到初始种群，否则，继续初始化，直到产生n个个体为止，将这n个个体作为初始种群；

步骤3计算每门课程的平均值xm，按照式(1)和(7)计算教学阶段产生新的学习者xnew，若xnew优于xold，则更新xold；若xnew还优于xteacher，则更新xteacher；

步骤4按照式(8)计算学习阶段产生新的学习者xnew，若xnew优于xold，则更新xold；若xnew优于xteacher，则更新xteacher；

步骤5按照式(9)产生新的变异个体，则更新全局最优个体xteacher；

步骤6置t=t+1，返回到步骤3，直到t达到设定的最大迭代次数,输出全局最优值.

4　数值实验及分析

4.1测试函数为了验证改进教-学优化算法的有效性，选取13个常见的约束问题测试函数[13-15]进行试验，13个测试函数都是被认为是用进化算法很难优化的复杂函数,主要特性如表1所示.在表1中, ρ=│F│/│S│是估计可行域占整个搜索空间的比率，│F│表示可行解的个数，│S│表示整个搜索空间随机产生解的个数，在实验中│S│=1 000 000，其中LI，NI，LE，NE分别表示约束优化问题约束条件中线性不等式、非线性不等式和线性等式和非线性等式的个数.

表1中的测试函数被认为利用随机优化算法很难优化的约束测试函数[14-15].问题g02，g03，g08和g12是极大化问题，利用-f(x)将其转化为极小化问题.问题g03，g05，g11和g13包含等式约束hj(x)=0，j=1，2，…，l，将其转化为不等式约束│hj(x)│-σ≤0，在本文中，σ=0.001.

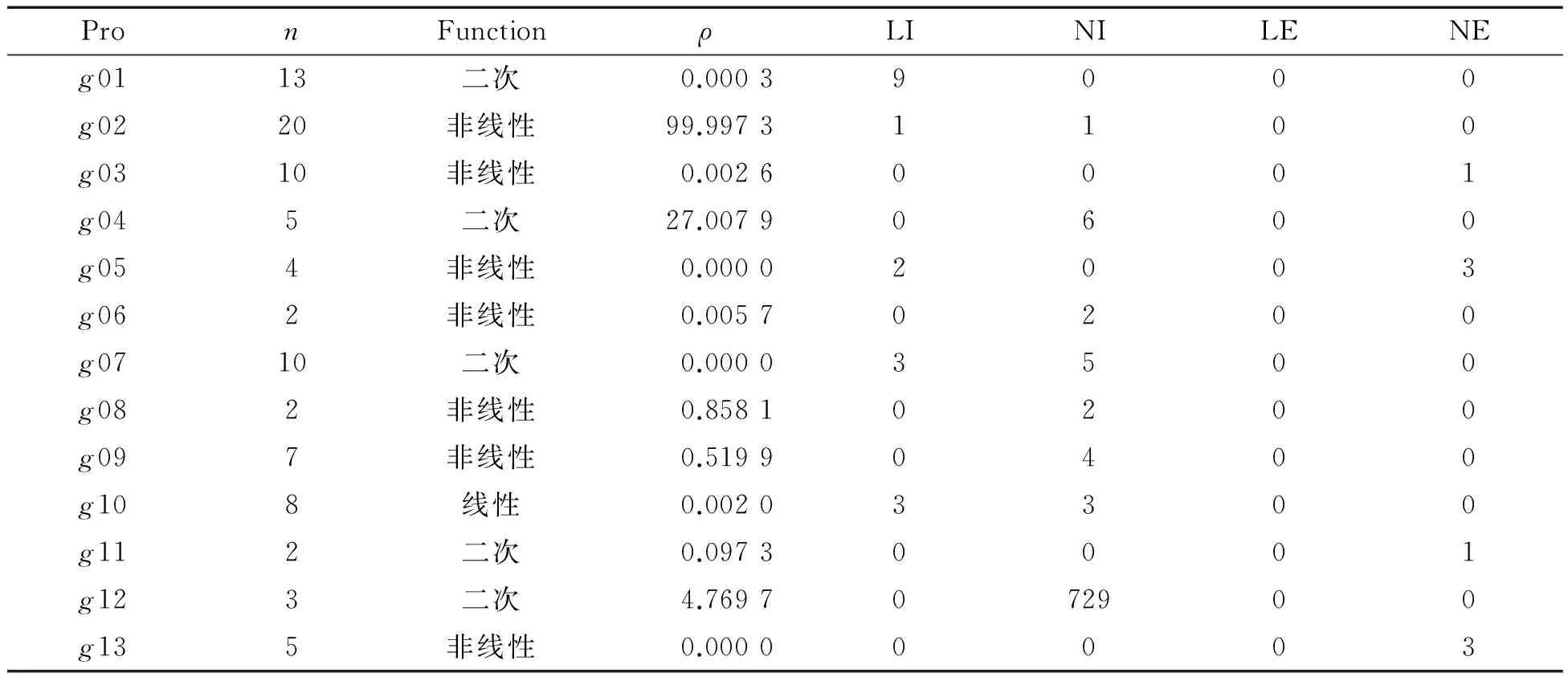
表1　测试函数的主要性质[15]

4.2测试结果与分析实验参数设置：种群大小n=500, 最大迭代次数Imax=3 000.从表1可以看出问题g05，g07和g13可行域的范围非常小(ρ=0.000 0)，在初始化过程中很难产生可行个体，因此约束违反度δ在g05中设为δ=0.15，在g07中为δ=0.015，在g13中为δ=0.025，其余的问题设为δ=10e-10.在问题g01，g10 和g13中，随机变异概率Pm=1，其余问题中变异概率pm=0.6.在方正台式机Intel(R)Pentium(R) D CPU 2.80 GHz,2.80 GHz, 内存1.00 GB上用Matlab 2010a进行实验，每个测试函数在相同的条件下独立运行30次，函数的最优值(记为Opt)以及30次实验的最好结果(记为Best)、中间值(记为Median)、最优值平均值(记为Mean)、最差结果(记为Worst)以及标准差(记为Std)如表2所示.

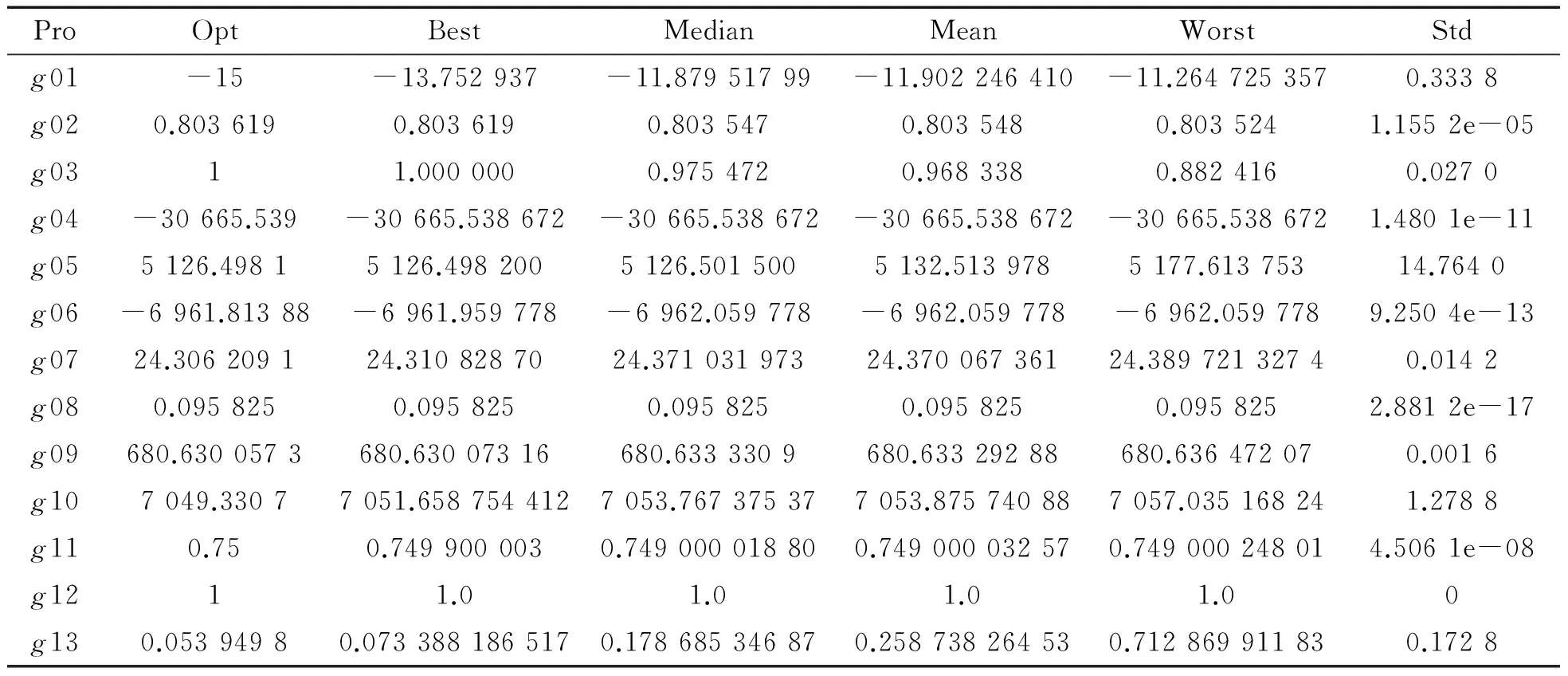
表2 ITLBO算法的实验结果

从表2中可以看出，改进教-学优化算法对于大多数约束优化问题基本上都找到了最优解，并且标准差也比较小.问题g02,g03,g04,g06,g07,g08,g09,g11和g12，改进教-学优化在30次独立试验中都达到了最优值；问题g05，g010和g13是很难用进化算法求解的优化问题，g05和g13包含有等式约束，而且可行域也非常小，虽然改进教-学优化算法没有达到最优解，但是与最优解的误差相对较小；问题g01有2个局部极小-13.000和-12.453 125，但是改进教-学优化算法30次独立实验算法都跳出这2个局部极小点.

为了比较算法的性能，将教-学优化算法与最新的3种算法ASCHEA[15]，SAVPSO[14]，IADE[11]已有的数值结果进行比较，比较结果见表3～5,其中NA表示没有公布的数据.

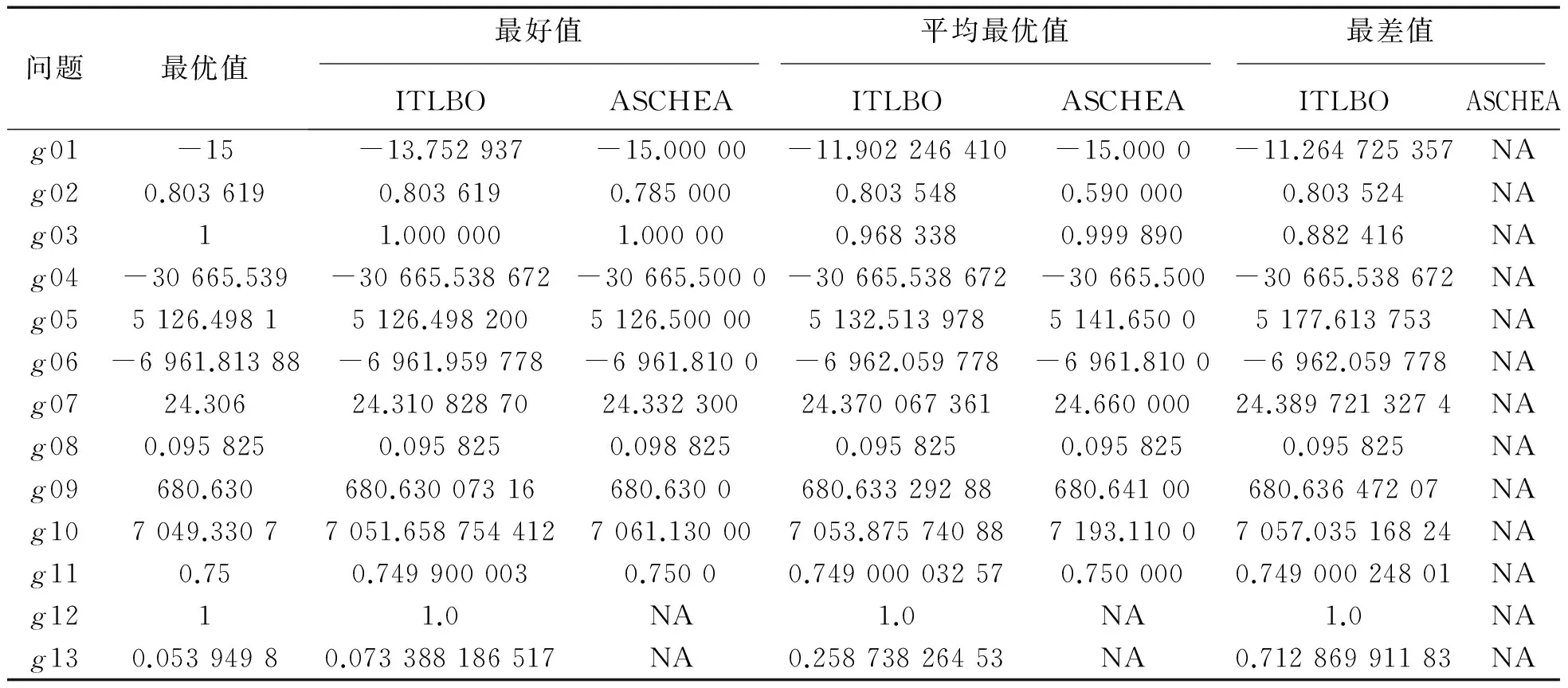
表3　改进教-学优化算法(ITLBO)与ASCHEA结果的比较表

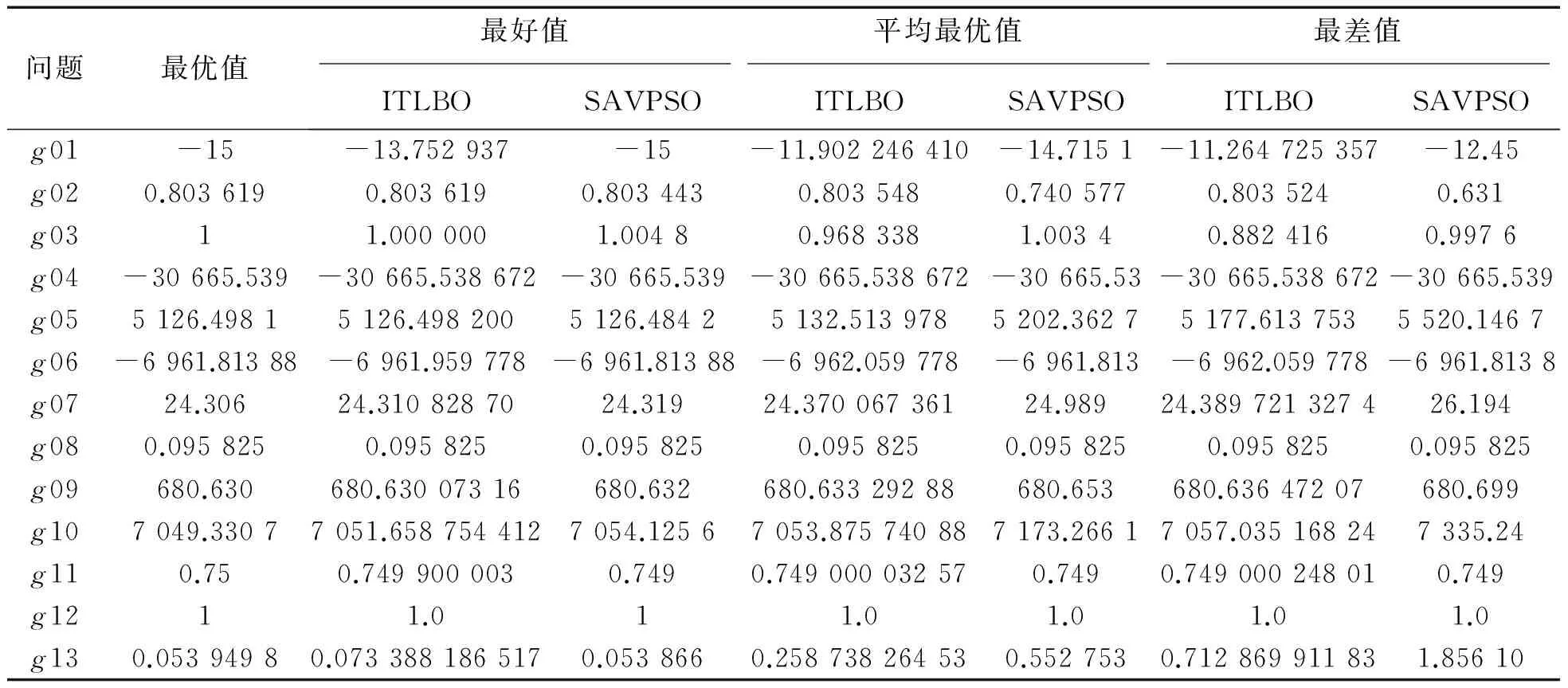
表4　改进教-学优化算法(ITLBO)与SAVPSO结果的比较表

表5　改进教-学算法(ITLBO)与IADE结果的比较表

表3是改进教-学优化算法与ASCHEA算法的比较结果，对于函数g02，g03，g04，g05，g07，g08，g09和g10，改进教-学优化算法不仅从30次运行的最好值，还是平均最优值，都比ASCHEA算法的寻优性能好，精度比较高，g12，g13以及最差值ASCHEA算法没有提供.SAVPSO算法是利用自适应速度改进的PSO算法来求解约束优化问题，是近年来提出的比较新颖的算法，从表4中可以看出，改进教-学优化算法的结果大部分优于或接近于SAVPSO算法.IADE算法是利用自适应改进差分进化算法求解约束优化问题，从表5中可以看出除过g01函数外，改进教-学优化算法的运行结果要优于IADE算法.所以从表3～5中可以看出改进教-学优化算法是有效的，可以求解大量的约束优化问题，同时对于测试函数g01以及含有等式约束的优化问题，但是改进教-学优化算法计算结果并不理想，如何提高算法的计算精度是今后进一步研究的课题.

5　结　论

针对约束优化问题，提出了一种求解约束优化问题的改进教-学优化算法.改进教-学优化算法提出了自适应的教学因子，受差分进化算法中变异策略的启发，对学习阶段的迭代方程进行改进，使得学习者的学习能力不仅受到学习者之间的相互影响，而且还受到当前最好学习者的影响，最后加入了随机变异策略，提高了算法的收敛速度，并应用于求解约束优化问题.通过13个测试函数实验表明，改进教-学优化算法具有较快的收敛速度和较好的全局寻优能力.

[1] Kenedy J，Eberhart R.Particle warm optimization:proceedings of IEEE International Conference on Neural Network 1995，Perth，November 27-December 1，1995[C].[S.l.]:IEEE.1995.

[2] 李敏强,冦纪淞,林丹，等.遗传算法的基本理论与应用[M].北京:科学出版社,2002.

[3] Storn R, Price K V. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization 1997,11: 341-359.

[4] Blum C.Ant colony optimization: Introduction and recent trends[J].Physics of life reviews, 2005,2(4): 353-373.

[5] Rao R V，Savsani V J，Vakharia D P . Teaching-learning- based optimization: A novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011,43:303-315.

[6] Rao R V，Savsani V J，Vakharia D P. Teaching-Learning-Based Optimization: An optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012,183:1-15.

[7] Venkata R，Patel V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J]. International Journal of Industrial Engineering Computations, 2012,3:535-560.

[8] Rao R V,Patel V. Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm[J].Applied Mathematical Modeling, 2013,37: 1 147-1 162.

[9] He Q, Wang L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J]. Engineering Applications of Artificial Intelligence, 2007, 20(1):89-99.

[10] Runarsson T P, Yao X. Stochastic ranking for constrained evolutionary optimization[J]. IEEE Trans. Evol. Comput, 2000, 4(3):284-294.

[11] 李会荣.非线性约束优化问题的自适应差分进化算法[J].计算机工程与应用,2011,47(25):44-48.

[12] Lu H, Chen W. Dynamic-objective particle swarm optimization for const rained optimization problems[J]. J Glob Optim, 2006, 12:409-419.

[13] Koziel S, Michalewicz Z. Evolutionary algorithms, homomorphous mapping and constrained parameter optimization[J]. Evolutionary computation, 1999,7(1):19-44.

[14] Lu H, Chen W. Self-adaptive velocity particle swarm optimization for solving constrained optimization problems[J]. Journal of Global Optimization，2008, 41(3): 427-445.

[15] Hamida B，Shoenauer M.ASCHEA:new results using adaptive segregational constraint handling:proceedings of the Congress on Evolutionary Computation 2002，Honolulu，May 12-17，2002[C].[S.l.]:IEEE，2002.

[16] 李会荣.基于单纯形局部搜索的自适应差分进化算法[J].海南大学学报(自然科学版),2013,31(2):143-148.

Improved Teaching-learning Based Optimization Algorithm for Constrained Optimization Problems

Li Huirong1, Zhou Yani2

(1. Department of Mathematics and Computer Application, Shangluo University, Shangluo 726000, China; 2. Department of Public Infrastructure, Shangluo Vocational and Technical College, Shangluo 726000, China)

In our report, an improved Teaching-Learning-Based Optimization (TLBO) algorithm for constrained optimization problems was proposed. Firstly, the adaptive teaching factor was proposed, which modified the iterative equation of learner phase and introduced the mutation strategy in the differential evolution algorithm; Secondly, the constraint violation function was used to convert the constrained optimization problems into unconstrained bi-objective optimization problem, in each iteration, keeping a part of the performance of better infeasible individuals is to maintain the diversity of the swarm. The numerical experiments showed that the proposed algorithm has faster convergence speed and better ability of global optimization.

Teaching Learning-Based Optimization (TLBO) Algorithm; constrained optimization; differential mutation; teaching factor

2015-03-14

陕西省自然科学基础研究计划项目(2014JM2-6098);陕西省教育厅科研计划(15JK1221);商洛学院博士团队服务地方科技创新与经济社会发展能力提升专项(SK2014-01-22)

李会荣(1979-),男,陕西洛南人,副教授,硕士,研究方向：计算智能以及机器学习， E-mail:lihuirong417@163.com

1004-1729(2015)04-0333-07

TP 18

ADOl：10.15886/j.cnki.hdxbzkb.2015.0059