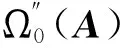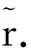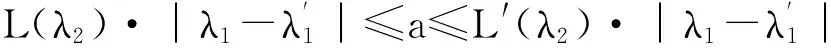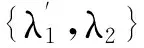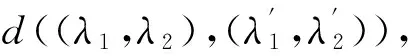一类由矩阵Kronecker积生成的分形与McMullen集的Lipschitz等价
单家俊,龙伦海,王司晨
(海南大学 信息科学技术学院, 海南 海口 570228)
一类由矩阵Kronecker积生成的分形与McMullen集的Lipschitz等价
单家俊,龙伦海,王司晨
(海南大学 信息科学技术学院, 海南 海口 570228)
首先阐述了利用矩阵Kronecker积迭代生成分形的方法, 与IFS迭代函数系生成的分形不同,基于矩阵Kronecker积迭代生成的分形与初始集的选择有关,若其初始集为正方形,则生成的分形即为McMullen集;其次利用定比分点构造了凸四边形和扇环与正方形之间的双Lipschitz映射,证明了如果将初始集由正方形换成任意一个凸四边形或圆心角小于180°的扇环,则由矩阵Kronecker积迭代生成的分形与McMullen集具有Lipschitz等价性.
分形; McMullen集; Hausdorff维数; 双Lipschitz映射
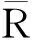
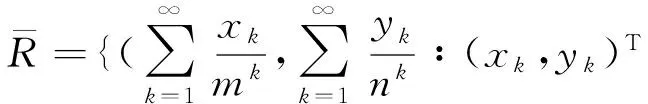
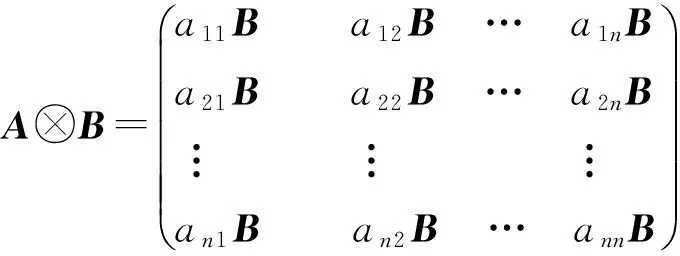
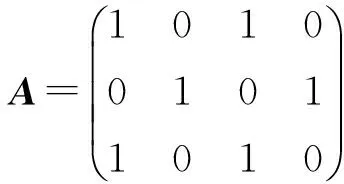
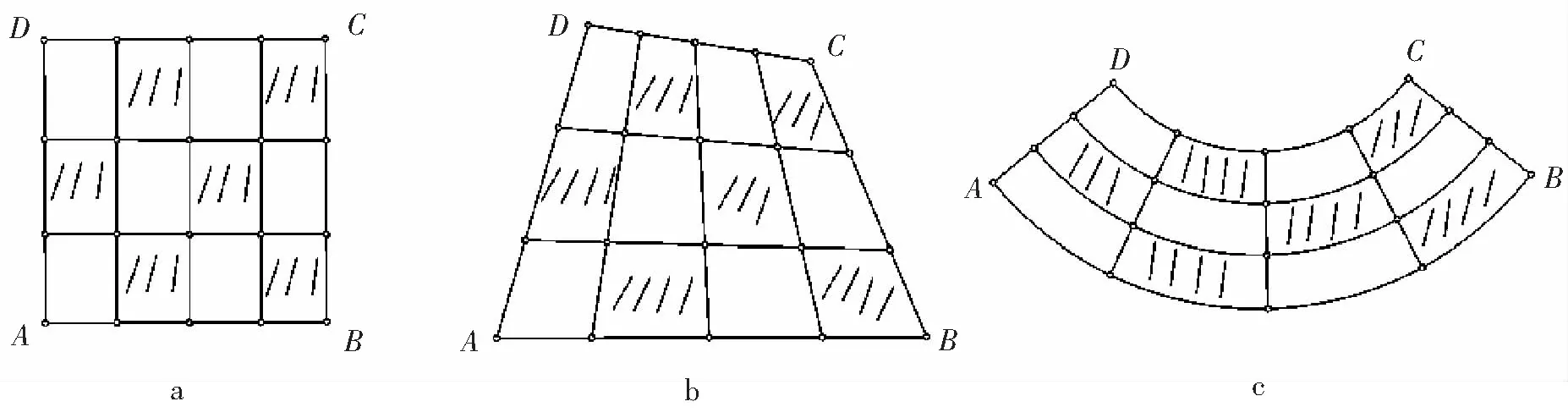
从几何的角度看,McMullen集的生成相当于在平面上对单位正方形的第一维边进行m等分,第2维边n等分,把正方形分割为m×n个小的长方形,长方形的左下顶点坐标记为(i,j),0≤i 利用矩阵Kronecker积的迭代,能生成一类严格分离的分形集. 与IFS迭代函数系生成的分形不同,基于矩阵Kronecker积迭代生成的分形与初始集的选择有关. 首先阐述了基于矩阵Kronecker积迭代生成分形的方法,其次利用定比分点构造了正方形与凸四边形、扇环之间的某种双Lipschitz映射,使得利用矩阵Kronecker积迭代、初始集为凸四边形或圆心角小于180°的扇环生成的分形集与McMullen集Lipschitz等价,进而二者与McMullen集具有相同的Hausdorff维数. 定义1设Rn中的任意非空子集E,{Ui}为E的一个有限或可数个直径不超过δ的覆盖,E⊆∪Ui,则称{Ui}为E的一个δ覆盖. 设s≥0,称 为E的Hausdorff测度,称 dimHE=sup{s∶Hs(E)=∞}=inf{s∶Hs(E)=0} 为E的Hausdorff维数. C1d(x1,x2) ≤D(f(x1),f(x2)) ≤C2d(x1,x2) 成立,则称f是双Lipschitz映射. 对于双Lipschitz映射,有以下引理成立: 引理1[2]如果f为双Lipschitz映射,则dimHE=dimHf(E). 平面上凸四边形和扇环中,利用定比分点容易得到以下性质. 性质1 如图1(a),凸四边形ABCD中,点E,F分别是线段AB,DC的λ1分点,点G,H分别是线段AD,BC的λ2分点,连接线段EF,GH交于点I,则点I分别是线段GH的λ1分点和线段EF的λ2分点. 图1 凸四边形、扇环和三角形 对于平面上的三角形,有以下性质成立. 为了证明本文的结论,还需要用到以下不等式. 性质4 0≤λ≤1,0≤θ≤π,不等式1-cos(λθ)-λ2(1-cosθ)≥0成立. 证明令f(θ)=1-cos(λθ)-λ2(1-cosθ),则 f ′(θ)=λsin(λθ)-λ2sinθ, f ″(θ)=λ2(cos(λθ)-cosθ). 因为函数y=cosx在[0,π]上是单调递减,0≤λ≤1,所以cos(λθ)-cosθ≥0,故f ″(θ)≥0. 从而有f ′(θ)在[0,π]上是单调递增,于是得到f ′(θ)≥f ′(0)=0,所以函数f (θ)在[0,π]上也单调递增,故f(θ)≥f(0)=0,不等式得证. 简写为A⊗B=(aij·B)mp×nq. 由定义4可以看出,矩阵Kronecker积的运算A⊗B本质上是将矩阵B嵌入矩阵A元素的每一个位置并与其作数乘运算,一般情况下A⊗B≠B⊗A. 记矩阵A的n次Kronecker积乘幂为A(n). 下面阐述基于矩阵Kronecker积迭代生成的分形方法,为简化起见,下文使用的矩阵元素均为0和1,元素非0和1的情况可以参考文献[9]中定义矩阵的广义Kronecker积. 设A=(aij)m×n为元素均为0和1且至少包含2个1的矩阵,其中m≥n≥2. 令A0=(1)为1阶单位矩阵,∀n=1,2,3,…,取 An=An-1⊗A=A(n), 其中,⊗为矩阵的Kronecker积. 现在考虑更换迭代的初始集为凸四边形或扇环. 图2 正方形、凸四边形与扇环按照矩阵A 的第一次迭代 将在正方形与凸四边形和扇环之间构造双Lipschitz映射,得到以下结论. 下面构造双Lipschitz映射f和g. 如图3所示,在正方形Ω0(A)中,将线段AB的λ1分点E与线段DC的λ1分点F相连,再将线段AD的λ2分点G与线段BC的λ2分点H相连,2条线段交于一点,记为(λ1,λ2). 图3 双Lipschitz 映射f和g (1) (2) 成立. 下面证明式(2),式(1)证明可参考文献[4]. 图4 扇环 (3) (4) (5) (6) (7) 成立,于是g为双Lipschitz映射. 证毕. [1]McMullenC.TheHausdorffdimensionofgeneralSierpinskicarperts[J].NogayaMath.J.,1984,96:1-9. [2]FalconerKJ.Fractalgeometry-mathematicalfoundationsandapplications[M].[S.l.]:JohnWiley, 2014. [3]FalconerKJ.Fractalgeometry:mathematicalfoundationsandapplications[M].NewYork:JohnWilley&Sons, 2003. [4] 奚李峰. 从平面几何题中引申出的维数计算[J].浙江万里学院学报,1999(4):29-31. [5] 朱志勇,文志雄. 一类广义Sierpinski地毯的Huasdorff维数[J].应用数学, 2011,24(2):360-365. [6] 张贤达. 矩阵分析与应用[M].第2版.北京:清华大学出版社, 2013:71-74. [7]LlorenteM,MattilaP.Lipschitzequivalenceofsubsetsofself-conformalsets[J].Nonlinearity, 2010, 23:875-882. [8] 朱莉红,陈绍明,龙伦海. 平面上广义McMullen集的Hausdorff维数[J].海南大学学报(自然科学版),2012,30(4):320-324. [9] 韩伟.Kronecker乘积生成分形图形和放大图像[J].哈尔滨理工大学学报,2011,16(2):49-52. [10] 龙伦海,梁丽,朱莉红. 由点矩阵的表示生成的分形矩阵的维数[J].数学进展,2015,44(2):229-238. Lipschitz Equivalence Between a Kind of Fractals Generated by Matrix Kronecker Product and McMullen Set Shan Jiajun, Long Lunhai, Wang Sichen (College of Information Science and Technology, Hainan University, Haikou 570228, China) In our report, the method of generating fractals based on the matrix iteration of Kronecker product was discussed. Different from the fractals generated by iterated function systems, the fractals generated by the matrix iteration of Kronecker product might be related to the choice of the initial set. If the initial set was square, the fractals were the McMullen set; The definite proportion and separated points were used to construct a bi Lipschitz map among convex quadrilateral, sector ring and square, and it was proved that if the initial set was changed from the square to an arbitrary convex quadrilateral or sector ring which central angle less than 180°,the fractals would be Lipschitz equivalent with McMullen set. fractals; McMullen set; Hausdorff dimension; bi Lipschitz map 2015-06-08 国家自然科学基金(11461016);海南省自然科学基金 (113003) 单家俊(1992-),男,江西南昌人,2013 级硕士研究生,研究方向:分形几何及其应用,E-mail:15501863129@163.com 龙伦海(1965-),男,重庆大足人,教授,博士,研究方向:分形几何及其应用,E-mail:13118900189@163.com. 1004-1729(2015)04-0299-06 O 174.12 A DOl:10.15886/j.cnki.hdxbzkb.2015.00531 预备知识
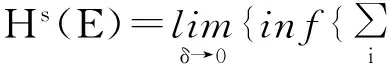
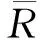



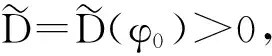
2 基于矩阵Kronecker积迭代生成的分形

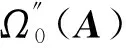
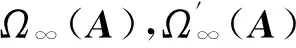
3 定理1的证明