略论二项式的系数计算
张青娟,潘东海,张艺萍,杨 凡
(1.中水北方勘测设计研究有限责任公司,天津 300222;2.天津市新华职工大学,天津 300041;3.天津城市职业学院,天津 300250)
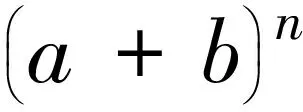
张青娟1,潘东海1,张艺萍2,杨 凡3
(1.中水北方勘测设计研究有限责任公司,天津 300222;2.天津市新华职工大学,天津 300041;3.天津城市职业学院,天津 300250)
本文论述了二项式系数计算的四种方法和它们在结构力学中应用的一个例子。这四种方法是杨辉(Pascal)三角法、二项式定理、系数递推法和线性方程组法,其中线性方程组法已脱离了杨辉(Pascal)三角系统成为一个新的方法,简单明了。它们在结构力学中的应用也是初步尝试。
杨辉(Pascal)三角法;二项式定理;系数递推法;线性方程组法
一、杨辉(Pascal)三角法


图1

二、二项式定理
基于杨辉(Pascal)三角法,而建立起来的二项式定理为:
①
其系数:
②
这一定理说明二项式展开式的系数与a、b的取值无关。同时说明①式为齐次多项式,a为降幂,b为升幂。其它特性亦可由②得出。如:

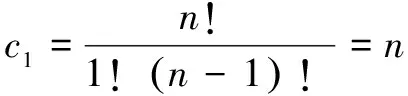
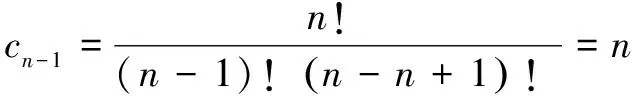

系数的对称性:
i与n-i为对称项,于是
因此,ci=cn-i(这是组合数学公式之一)
这就是二项式系数的对称性。
二项式定理把杨辉(Pascal)三角的特性通过数学归纳法,扩充到了任意n值,这样在理论上很有价值,尤其在组合数学中,基于二项式定理导出许多很有用的公式。二项式定理不仅能计算二项式的系数,它更是计算许多问题的一种重要方法和工具。
三、系数递推法
笔者之一在文献③中给出了一个计算二项式系数的简便方法——系数递推法,该法可用一句话来说明:“前一项的系数值,乘以前一项a的指数,再除以前一项b的指数加1,即为下一项的系数”。写成公式如下:
③
这一公式非常容易记忆。因为由①式可知ck的k正好与b的指数一一对应,因此也就知道了a的指数为n-k,而前一项ck本身也为已知,这样就可以从k=0,1,2,3,…,n逐项计算出来。
该式比原二项式定理要便捷、易记。其实ci+1与ci相比,即为此式。
倘若计算某n值的指定k项的系数时,可按下式计算:
④
k0=1,k1=n
④式容易证明,根据系数递推法,ck由ck-1组成,ck-1又由ck-2组成,等等,即可导出④式。但这算式有不理想的地方,通用性太差,k0和k1都计算不出来。实际上,④式分子分母都乘以(n-k)!后:
此即二项式定理。这也就是为什么二项式定理不把分子、分母的共同因子(n-k)!消去的原因。
至此,可以看到系数递推法主要优点是比原定理——二项式定理简单、易记,实用性更强。
四、线性方程组法
从上面所述,已经知道,二项式的系数与a、b的取值无关。但利用a、b的不同取值,却可算出各系数。
令a=1,2,3,···,n+1;b≡1,则①式可写成如下形式:
该行列式显然不为0,故可唯一地解出c0,c1…cn诸系数。
该法利用了①式,而①式可由(a+b)n的定义直接导出。它就完全脱离了杨辉(Pascal)三角系统,一目了然,成为一个新法。
五、例题
N=7时,求二项式的各系数。
当n=7时,有4个边界条件已知,即1、7和7、1,又有对称性,故仅由两个方程式即可求得。现选择n=7的前两个方程:
c0+c1+c2+c3+c4+c5+c6+c7=27
27c0+26c1+25c2+24c3+23c4+22c5+2c6+c7=37
去掉边值,利用对称性有:
c2+c3=56
3c2+2c3=133
∴c2=21
c3=35
故其解为:1,7,21,35,35,21,7,1。
这同杨辉(Pascal)三角的第七级是一样的。
六、在某些力学计算中的应用
二项式定理在数学及其他领域中多有应用。本文在结构力学中进行了初步探索,其方法如下。
一个由等腰对称三角形组成的刚架,顶点受垂直单位荷载压力,计算各层的压力分布。顶点将单位垂直压力一分为二的向下传递,类似杨辉(Pascal)三角法的传播规律,如图2所示。提出各层的分母后,留下的分子即为杨辉(Pascal)三角,见图3。单位荷载在各层的分布可视为扩散系数,扩散系数乘实际顶点压力即为各层所受压力。如实际顶点垂直压力为500吨,在第五层的分布为:


它们之和为500吨。
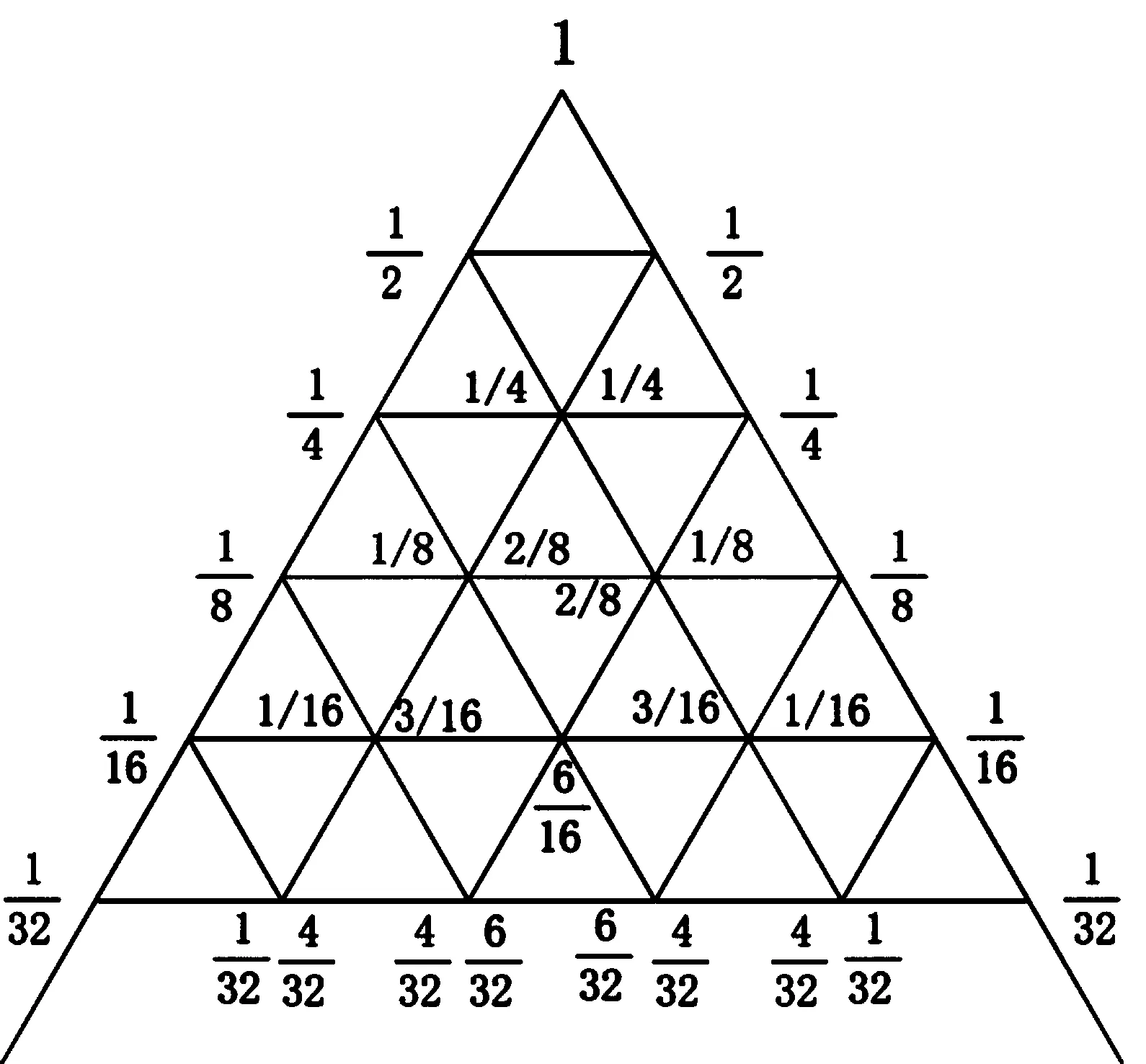
图2

图3(提出分母,即为杨辉(Pascal)三角)
七、结论
本文提供了多种形式的有关二项式系数的计算方法。从本文看,前三种方法大同小异,系数递推比较简便、快捷、易记,是它的一大特点。当n相当大时,可由线性方程第一分支进行初步检查,如不满足,一定计算有误。它只是必要条件。对于重要的计算,也可代入线性方程组,看是否都满足,如都能满足,则计算是成功的。
线性方程组法在现代电子计算机技术如此发达时代解大型方程组不成问题,况且边界点有四个已知,利用对称性再减去一半的工作量。所以也有实用价值。该法的意义是脱离了传统方法,另成一种简单明了的方法。上述应用的例子,只是结构力学的一个单元,如何应用于真实结构,将另文探讨。
[1]华罗庚.从杨辉三角谈起[M].北京:人民教育出版社,1964.
Brief Review on Calculation of Coefficient of Binomial (a+b)n
ZHANG Qing-juan1, PAN Dong-hai1, ZHANG Yi-ping2, YANG Fan3
(1.RecycledWaterNorthSurveyDesignResearchCo.,LTD,Tianjin, 300222;2.TianjinXinhuaStaffUniversity,Tianjin, 300052;3.TianjinCityVocationalCollege,Tianjin, 300250)
the papers discusses four methods to calculate the coefficient of binomial (a+b)n. An example applied in structural mechanics is also cited. The four methods are Pascal triangle method, binomial theorem, coefficient recursion method and system of linear equations. The last method - system of linear equations has broken away from the Pascal triangle method and developed to be a new method, simple and easy to use. It is also the first time to attempt to apply the four methods in structural mechanics.
Pascal triangle method; binomial theorem; coefficient recursion method; system of linear equations
2014-09-12
张青娟(1963-),女,陕西人,中水北方勘测设计研究有限责任公司高级工程师,主要从事计算机应用方面研究。
O13
A
1673-582X(2015)02-0089-04

