高超声速飞行器模型振动及传力特性研究*

文 娟, 刘伟雄， 高宏力， 黄海凤， 张筱辰， 李世超

(1．西南交通大学机械工程学院 成都，610031) (2.中国空气动力研究与发展中心 绵阳，621000)



高超声速飞行器模型振动及传力特性研究*

文 娟1, 刘伟雄2， 高宏力1， 黄海凤1， 张筱辰1， 李世超1

(1．西南交通大学机械工程学院 成都，610031) (2.中国空气动力研究与发展中心 绵阳，621000)

提出了一种应用加速度信号研究飞行器试验模型传力特性的方法，采集飞行器试验模型不同位置的振动加速度信号，应用小波包分解方法对采集到的加速度信号进行预处理。对滤波后的信号采用经验模态分解(empirical mode decomposition, 简称EMD)方法进行处理，得到信号的本征模态函数(intrinsic mode functions，简称IMFs)，并通过相关系数判别并剔除伪分量。对剩余IMF分量进行希尔伯特(Hilbert)变换，得到信号的希尔伯特谱，并计算不同方向上飞行器试验模型壳体与内部结构加速度信号的能量分布差异，判断各方向上飞行器试验模型传力特性的优劣。结果表明：该方法能够用于飞行器模型的传力特性研究，且飞行器模型各向传力误差分别为0.189 1,0.098 1,0.0377，大部分气动载荷能够有效地从飞行器壳体传递到其内部结构，垂直方向上的力学传递性能最佳。

高超声速； 经验模态分解； 希尔伯特变换; 飞行器模型； 传力特性

引 言

航空航天飞行器的研制过程中，为了掌握飞行器性能、降低飞行器研制风险和成本，通常会进行风洞模型试验。在各种试验条件下对飞行器试验模型受到的气动力和力矩进行测量，是风洞试验中最基本的实验项目[1-5]。风洞试验中，通常采用测力天平对飞行器试验模型所受到的气动载荷进行测量，而飞行器试验模型所受到的载荷通常要经过模型内部结构才能传递至测力天平。因此，飞行器模型传递性能会直接影响风洞试验的准确度。

经验模态分解能够自适应地将非平稳、非线性信号分解成一系列本征模态函数。对经验模态分解得到的本征模态函数进行Hilbert变换，将会得到信号的希尔伯特-黄变换(HHT)谱，这一过程统称为经验模态分析[7-9]。经验模态分析能够精确地做出时间-频率图，是一种自适应性的时频局部化分析方法[9]。目前，该方法已经在故障诊断、地震监测等领域得到广泛应用[10-13]。

目前，国内关于飞行器风洞试验模型内部结构力学传递特性研究较少，而应用信号处理方法研究飞行器风洞试验模型传力特性的方法还未见报道。笔者将经验模态分析方法引入飞行器试验模型力学传递特性分析中，对飞行器试验模型不同位置采集到的振动加速度信号进行经验模态分析，研究不同位置振动加速度信号HHT谱及能量分布的差异，从而研究飞行器模型传力特性的优劣。

1 经验模态分析

经验模态分析包括两部分内容，即经验模态分解和希尔伯特谱分析。它把原序列分解成有限个内在的、固有的本征模态函数分量；然后对每一个分量施行希尔伯特变换，得到相应的希尔伯特谱，通过分析各个分量及其希尔伯特谱，揭示原序列的多尺度振荡变化的特征[14]。

EMD方法的关键技术问题，是如何把一个非线性非平稳序列分解为有限个IMF分量和一个趋势项。对一原始信号X(t)，分解结束后，原信号X(t)可以表示为

(1)

其中：c1,c2,…,cn分别为信号从高到低不同频率段的IMF分量；rn为信号平均趋势的残余项。

对每一个IMF分量进行Hilbert变换之后，可把原始信号表示为

(2)

式(2)可把信号幅度在三维空间中表达成时间与瞬时频率的函数，信号幅度也可表示为时间-频率平面上的等高线，这种经过处理的时间频率平面上的幅度分布称为Hilbert时频谱，即Hilbert谱[15-17]。

2 模型加速度信号的采集

为了模拟飞行器的真实工作环境，从而分析实际情况下飞行器所受到的气动力与传力特性，必须进行风洞试验。由于试验中的飞行器模型为高超声速飞行器模型，因此试验中需要给定的风速必须与飞行器工作时速度一致。与普通风洞试验相比，高超声速风洞试验难度大很多，对试验模型与试验设备的要求更高。为了采集高超声速工况下的振动加速度信号，本次试验在某脉冲燃烧风洞中进行。

试验前，为了了解飞行器试验模型的动力学特性，对该模型进行了模态测试。本次试验中采用锤击法，通过固定参考点移动力锤方式进行。将加速度传感器固定在飞行器试验模型上，移动力锤敲击飞行器试验模型，力锤的力信号与加速度计采集到的信号通过采集仪送入计算机。模态测试系统框图如图1所示。

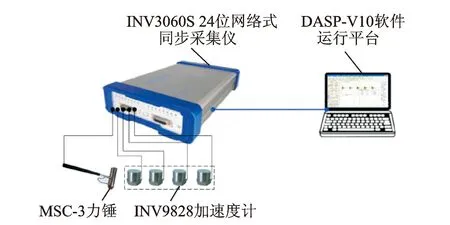
图1 模态测试系统框图Fig.1 The diagram of modal testing system

图2 飞行器试验模型动力学特性示意图Fig.2 Dynamic characteristic of the vehicle model

采用北京东方振动和噪声技术研究所的DASP-V10软件运行平台对采集到的数据进行分析，得出模态试验结果，包括飞行器试验模型的模态振型和固有频率，图2中一阶振型频率为49.087Hz,[1]为模型的一阶固有频率。为了确保试验结果的准确性，减少因模型固有振型差别造成的影响，必须选择振动特性相同的点作为振动加速度信号采集点，且模型头锥部的温度高，因而应当避开这部分区域。通过观察模型各阶模态振型，并考虑加速度传感器安装的可行性，选取振动特性相同的两点，即试验模型壳体上的1点，以及模型内部结构上的2点作为测试点。

试验前，将飞行器模型安装在特定的试验台上。振动加速度信号获取试验台安装方式如图3所示，测力天平3置于飞行器试验模型中，整个模型固定于支座4上。

根据选择的测点，考虑到高超声速环境下，飞行器表面的温度很高，而模型壳体内部由于热防护材料的隔离，温度相对较低。因此，将两个三向加速度传感器安装在模型顶端正中央壳体内部(1a处)和内部结构正中央(2a处)。传感器的信号输出端均与特定电缆相连，将信号从风洞传输到信号调理仪上，信号调理仪与计算机相连，获取高超声速工况下的振动信号。

1-壳体；1a-壳体内部；2-内部结构；2a-内部结构正中央；3-测力天平；4-支座图3 试验台立体结构示意图Fig.3 Installation of the test bed

在信号的采集过程中，采样频率的选择十分关键，采样频率是否合适关系着信号的准确性与完整性。为了确定此次试验的采样频率，将以往试验中得到的振动加速度信号进行FFT变换，得到其频谱图如图4所示。由图4可知，飞行器试验模型的振动频率几乎在20kHz以下。因此，根据Nyquist采样定理，本次试验选取50kHz采样频率采集飞行器壳体及内部结构的振动加速度信号。为了确保采集的信号不失真，所选传感器的有效测量频带为0.5～16kHz。

图4 飞行器模型振动信号的FFT变换Fig.4 Result of FFT

试验时，采用马赫数为8的风速模拟实际工况对飞行器试验模型进行风洞试验。在气动力的有效作用时间内，采集飞行器试验模型壳体与内部结构的振动加速度信号。

3 振动加速度的经验模态分析

常用的信号处理方法有时域分析、频域分析和时频分析。由于飞行器试验模型的壳体与内部结构所使用的材料与结构不同，因而二者振动加速度的时域特性存在较大的差异性。此外，虽然气动力稳定作用时间很短，但由于风洞试验的特殊性，模型的振动加速度信号为非线性非平稳时间序列。因此，必须从时频分析的角度来考查壳体与内部结构信号的差异性。

为了从时频特性的角度研究飞行器模型的振动加速度，必须对采集到的加速度信号进行一定的处理。以壳体轴向信号为例，对其进行经验模态分析，得出该信号的时频分布特征。

3.1 振动加速度信号的预处理

由于振动加速度信号的采样频率为50kHz，频带较宽，若直接对其进行EMD分解，则会增加EMD分解的层数和计算量，降低分解的时效性，甚至使EMD分解失去实际物理意义[17]。因此，应当适当缩小振动信号的频宽。小波包分析能够将频带进行多层次划分，且能够根据被分析信号的特征，自适应地选择相应频带进行重构实现自适应滤波。为了缩小壳体振动加速度信号的频宽，对信号进行3层小波包分解，并计算其各个子带的能量百分比(如图5所示)。由图5可知，振动加速度信号能量主要集中在子带1～子带4。因此，选择子带1～子带4进行重构，实现壳体振动加速度信号的低通滤波，滤波后信号的频率范围为0～12.5kHz。

图5 轴向加速度各频带能量百分比Fig.5 Wavelet energy for various frequency band

3.2 振动加速度的经验模态分析

对滤波后的加速度信号进行EMD分解的结果如图6所示。

图6 轴向加速度EMD分解结果Fig.6 Result of EMD resolution

图6中，IMF1～IMF13为本征模态函数，R13为残余分量。在EMD的分解过程中由于局部均值数值计算方法的插值误差、边界效应以及终止判据不严格等原因[18]，会导致EMD分解出的IMF分量比信号的实际组成分量多，通常把这些多余的分量称为“伪分量”。为了剔除这些伪分量，通过求各IMF分量与原信号的相关系数ρs,ci来判断各IMF分量的真伪，如表1所示。

由表1可知：IMF2，IMF3，IMF4和IMF5与原信号的相关系数较大，其他IMF分量的相关系数较小，均为伪分量予以剔除。对振动信号的实际IMF分量进行Hilbert变换得到其HHT谱如图7所示。

表1 各IMF分量与轴向加速度的相关系数

Tab.1 The correlation coefficients for each IMF and axial acceleration

IMF分量ρs,ciIMF分量ρs,ciIMF10.1752IMF80.0701IMF20.6407IMF90.0514IMF30.3480IMF100.0353IMF40.5073IMF110.0476IMF50.3260IMF120.0089IMF60.0692IMF130.0105IMF70.0384

图7 壳体轴向加速度HHT谱Fig.7 HHT spectrums of axial acceleration on aerodynamic configuration

由图7可知：IMF2，IMF3，IMF4和IMF5为4个频率随时间波动的IMF分量，其总体频率分布由高到低。具体地，IMF2的中心频率为5 kHz，频率范围为2～8 kHz；IMF3的中心频率为3 kHz，频率范围为1～5 kHz；IMF4的中心频率为1 kHz，频率范围为0～2 kHz；IMF5的中心频率为500 Hz，频率范围为0～1 kHz。

4 飞行器模型的传力特性分析

风洞试验中，壳体将其所受到的气动载荷传递至内部结构上，再由该内部结构将力传递至天平，由天平测出模型所受气动力。因此，飞行器模型传力特性的优劣直接影响风洞试验数据的准确性。为了分析飞行器模型的传力特性，对壳体及内部结构上的振动加速度进行测试，通过比较两个不同构件上的振动加速度数据来反映飞行器模型的振动特征和载荷传递规律。因此，下面将对壳体与内部结构3个方向的振动加速度进行对比，以分析飞行器模型的传力特性。

4.1 模型轴向传力特性

采用3节中所述的振动加速度信号分析方法，对内部结构的轴向加速度信号进行时频分析，得到该信号的HHT谱如图8所示。

图8 内部结构轴向加速度HHT谱Fig.8 HHT spectrums of axial acceleration on the inner structure

对比图7和图8可知，壳体与内部结构各IMF分量均为随时间波动的分量，二者的中心频率几乎相同，均在5，3，1 kHz及500 Hz附近，各IMF分量的频率范围也大致相同。但二者各IMF分量的能量有所不同。

为了定量分析两组信号各IMF分量在能量上的差异，计算各IMF分量占总能量的比值，并比较两组信号各IMF分量占信号总能量的比值来确定两组信号各IMF分量在能量上的差异。

具体的计算步骤如下：

1) 分别计算飞行器模型壳体轴向加速度信号X1(t)各有效IMF分量的能量E1(i)，对E1(i)进行求和，得到信号总能量E1;

3) 同理，得到模型内部结构轴向加速度信号X2(t)各有效IMF分量占总能量比值θ2(i)；

4.2 模型径向传力特性

采用上述方法分别对壳体与内部结构的径向振动信号进行经验模态分析。结果表明：内部结构径向振动加速度信号与壳体径向振动加速度信号的HHT分布在频域上存在一定的差异。其中，内部结构径向振动加速度信号的IMF2分量中心频率为6kHz，大于壳体的IMF2分量中心频率，同时，其频率范围为2～10kHz，较壳体横向振动信号的IMF2分量范围更广；内部结构横向振动信号IMF3分量的中心频率为4kHz，频率范围为2～6kHz，均与壳体横向振动信号IMF3分量不同，但与壳体横向振动信号IMF2分量的分布相同；其IMF4分量的中心频率为2kHz，频率范围为1～3kHz，整体波动频率高于壳体横向振动信号IMF4分量；而内部结构横向振动信号IMF5分量和IMF6分量的中心频率与频率范围分别与壳体横向振动信号IMF4分量和IMF5分量相似，但能量相对较低。

4.3 模型垂向传力特性

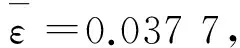
某研究所前期工作得出天平轴向气动力测试存在一定误差，而天平径向与垂向测试结果较准确。本研究结果与这一结论具有较好的一致性，因而能够采用提出的方法研究飞行器模型的传力特性。

5 结 论

1)EMD方法能够把复杂的飞行器模型振动加速度信号中蕴含的本征模态函数分解出来，对分解出来的IMF分量进行HHT变换，能够得出信号随时间和频率的变化规律，便于观察飞行器模型振动信号特征。

2) 通过比较壳体与内部结构振动加速度信号的IMF分量HHT分布，并计算不同位置上振动加速度信号能量的差异，能够分析飞行器模型力学传递特性的优劣。

3) 壳体轴向振动加速度信号与内部结构轴向振动加速度信号的中心频率分布相似，但能量传递存在一定的差异，大部分轴向气动载荷能够很好地传递至内部结构。内部结构径向振动加速度信号与壳体径向振动加速度信号的HHT分布相比，多了一个中心频率为6kHz的高频波动分量，其余分量的信号分布规律相似，且能量传递误差较小，说明径向气动力能够较好地传递至内部结构。与轴向振动信号和径向振动信号相比，飞行器模型的垂向振动加速度信号主要集中在高频段，壳体的振动频率高于内部结构的振动频率，但能量传递误差仅有0.037 7，因而能量能够在各频率段得到很好的传递，飞行器试验模型在垂直方向上具有很好的力学传递性能。

4) 由于客观条件的限制，笔者只选取了两点研究飞行器试验模型的力学传递特性。在后续研究中将选择更多的测试点，提高飞行器模型传力特性研究的准确性。

[1] Huang Yong, Dong Lixin, Zhao Kecheng, et al. On the correlation of force test results of a tactical missile calibration model in five different wind tunnels[J]. Liuti Lixue Shiyan yu Celiang, 2002, 16(2): 16-20.

[2] Satheesh K, Jagadeesh G. Analysis of an internally mountable accelerometer balance system for use with non-isotropic models in shock tunnels[J]. Measurement, 2009, 42(6): 856-862.

[3] Johnson T H, Parker P A, Landman D. Cal-ibration modeling of non-monolithic wind-tunnel force balances[J]. Journal of Air-craft, 2010, 47(6): 1860-1866.

[4] 陈德华, 尹陆平, 吴文华, 等. 2.4 米跨声速风洞大展弦比飞机测力试验技术研究[J]. 空气动力学学报, 2009, 27(5): 542-546.

Chen Dehua, Yin Luping, Wu Wenhua, et al. The test technique for aircraft with high aspect ratio in the 2.4 meter transonic wind tunnel[J]. Acta Aero-dynamica Sinica, 2009, 27(5): 542-546. (in Chinese)

[5] 解亚军, 叶正寅, 白静, 等. 微型飞行器测量天平设计与风洞试验[J]. 实验流体力学, 2006, 20(1): 23-26.

Xie Yajun, Ye Zhengyin, Bai Jing, et al. Design of strain-gage balances for micro air vehicles and their experiments in wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(1): 23-26. (in Chinese)

[6] Peng Z K, Tse P W, Chu F L. An improved Hilbert-Huang transform and its appli-cation in vibration signal analysis[J]. Journal of Sound and Vibration, 2005, 286(1): 187-205.

[7] Huang N E, Wu Manli, Qu Wendong, et al. Applications of Hilbert-Huang trans-form to non-stationary financial time series analysis[J]. Applied Stochastic Models in Bus-iness and Industry, 2003, 19(3): 245-268.

[8] 黄迪山, 刘玉霞. 经验模态分解滤波器组特性及轴承异音识别[J]. 振动、测试与诊断, 2012, 32(2): 332-336.

Huang Dishan, Liu Yuxia. Characteristics of EMD filter bank and identification of abnormal sound of ball bearing[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(2): 332-336. (in Chinese)

[9] 李舜酩，郭海东，李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报, 2013, 34(8): 1907-1915.

Li Shunming,Guo Haidong, Li Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1907-1915. (in Chinese)

[10]Raja J E, Kiong L C, Soong L W. Hil-bert-Huang transform-based emitted sound signal analysis for tool flank wear monitoring[J]. Arabian Journal for Science and Engineering, 2013, 38(8): 2219-2226.

[11]Bi Mingxia, Huang Hanming, Bian Yinju. A study on seismic signal HHT features extraction and SVM recognition of earthquake and explosion[J]. Progress in Geophysiscs, 2011, 26(4): 1157-1164.

[12]Tang Xianguang, Guo Yu, Ding Yanchun. Rolling element bearing fault feature extraction based on HHT and indepen-dent component analysis[J]. Journal of Vibration and Shock, 2011, 30(10): 45-49.

[13]李方溪, 陈桂明, 朱露, 等. 基于经验模态分解与 RBF 神经网络的混合预测[J]. 振动、测试与诊断, 2012, 32(5): 817-822.

Li Fangxi, Chen Guiming, Zhu Lu, et al. Hybrid prediction method based on empirical mode decomposition and RBF neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5):817-822. (in Chinese)

[14]Zhou Yanhui, Chen Wenchao, Gao Jinghuai. Application of Hilbert-Huang transform based instantaneous freq-uency to seismic reflection data[J]. Journal of Applied Geophysics, 2012, 82: 68-74.

[15]Xu Kejun, Qin Haiqin, Jiang Longping. Rotor-case vibration signal analysis of an aero engine based on EMD and HHT[J]. Journal of Vibration and Shock, 2011, 30(7): 237-240.

[16]王保平, 王增才, 张万枝. 基于 EMD 与神经网络的煤岩界面识别方法[J]. 振动、测试与诊断, 2012, 32(4): 586-590.

Wang Baoping, Wang Zengcai, Zhang Wanzhi. Coal-Rock interface recog-nition method based on EMD and neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 586-590. (in Chinese)

[17]Xu Hongmei, Hao Zhiyong, Yang Chen. Study on the time-frequency charac-teristics of engine noise signal based on EMD and HHT[J]. Chinese Internal Combustion Engine Engineering, 2008, 29(6): 60-64,69.

[18]蔡艳平,李艾华,王涛,等. 基于EMD-W igner-Ville的内燃机振动时频分析[J]. 振动工程学报, 2010, 23(4): 431-437.

Cai Yanping, Li Aihua, Wang Tao, et al. I.C.engine vibration time-frequency analysis based on EMD-Wigner Ville[J]. Journal of Vibration Engineering, 2010, 23(4): 431-437. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.026

*国家自然科学基金资助项目(51275426)；中央高校基本科研业务费专项资金资助项目(2682014CX034)；西南交通大学轨道交通行业拔尖创新人才培育项目(西交校研[2014]1号)

2014-12-18；

2015-03-27

V22； TH39

文娟，女，1990年8月生，博士生。主要研究方向为机械设备寿命预测与故障诊断、信号采集与处理。曾发表《基于AT89S52单片机的智能小车设计及制作》(《企业技术开发》2011年第6期)等论文。 E-mail: jwen0739@163.com