移动质量简支梁耦合时变系统建模与实验设计*

马志赛， 刘 莉， 周思达， 杨 武

(北京理工大学飞行器动力学与控制教育部重点实验室 北京，100081)



移动质量简支梁耦合时变系统建模与实验设计*

马志赛， 刘 莉， 周思达， 杨 武

(北京理工大学飞行器动力学与控制教育部重点实验室 北京，100081)

建立了移动质量简支梁耦合时变系统的动力学模型,通过数值仿真分析了移动质量速度及加速度对耦合时变系统模态参数的影响，得到移动质量诱导产生的附加阻尼。设计并搭建移动质量简支梁实验系统，通过参考实验得到实验系统的初始阻尼，并分别采用频域和时域模态参数辨识方法对质量块不同移动速度下的实验系统进行辨识。结果表明，所建立动力学模型能够对移动质量问题进行准确描述，实验系统可为时变结构动力学分析的理论研究提供实验支持，特别是对时变结构模态参数辨识方法进行实验验证。

移动质量； 简支梁； 时变系统； 实验系统设计

引 言

实际工程结构的特性都是随时间变化的，特别是在航空航天、机械和桥梁等应用领域结构的时变特性不能被忽略。例如，火箭发射过程中，燃料快速消耗，火箭系统质量特性不断变化；飞行器超高速飞行时，气动加热会引起材料刚度和阻尼随时间变化；航天器太阳帆板的展开会引起结构质量与刚度特性发生变化；火车通过铁路桥时，车桥组合系统结构特性会随着火车的移动不断变化[1-2]。为更好地对各类时变结构进行分析与设计，有必要对时变结构的动力学分析方法展开研究，特别是对能够获取时变结构真实条件下整体动力学特性的实验模态分析[3]方法进行研究。Poulimenos等[4]通过一个质量块在简支梁上移动的实验系统验证了所提出的基于时间序列的辨识方法。Spiridonakos等[5]通过一个可伸缩的机械结构对所提出的基于振动响应的故障诊断方法进行了验证。Liu等[6]通过一个变长度悬臂梁实验系统验证了所提出的基于子空间的时变结构模态参数辨识方法。续秀忠等[7]搭建了变质量悬臂梁实验系统，通过改变悬臂梁上漏斗内水的质量实现了悬臂梁质量随时间的变化。充分考虑实验系统的物理意义、时变特征、结构特性随时间变化形式及其是否精确可控等因素，笔者以移动质量-梁耦合时变系统为对象开展动力学特性研究与实验设计。

很多工程结构都会承受移动的质量，如车-桥系统、弹-炮系统、重物-桥吊系统及滑块-导轨系统等，这些系统均可简化为移动质量-梁模型。移动质量-梁耦合系统本质上为时变系统，在已公开的文献中，将移动质量作用下梁结构的动力学响应问题归纳为3类[8-9]：移动载荷、移动质量和移动振子问题。移动载荷问题不考虑移动质量的惯性，王文亮等[10]给出了移动载荷作用下简支梁动力学响应的求解方法。移动质量问题考虑移动质量的惯性但认为其刚度无限大，Michaltsos等[11-13]分别讨论了移动质量惯性、向心力、科氏力、转动惯性以及加速度对简支梁动力学响应的影响。移动振子问题同时考虑了移动质量的惯性及其有限刚度，Biondi等[8]建立了考虑移动振子惯性情况下移动振子-梁耦合系统的动力学模型。

借鉴Biondi给出的建模方法，在仅忽略移动质量转动惯性的前提下，笔者建立了任意激励下移动质量-梁耦合时变系统的动力学模型，精度更高，适用范围更广。通过数值仿真分析了移动质量速度及加速度对耦合时变系统模态参数的影响，得到移动质量诱导产生的附加阻尼。设计并搭建移动质量简支梁实验系统，通过参考实验得到实验系统的初始阻尼，并分别采用频域和时域模态参数辨识方法对质量块不同移动速度下的实验系统进行了辨识。

1 动力学模型

如图1为移动质量-梁耦合系统，其振动微分方程为

Q(x,t)+P(x,t)

(1)

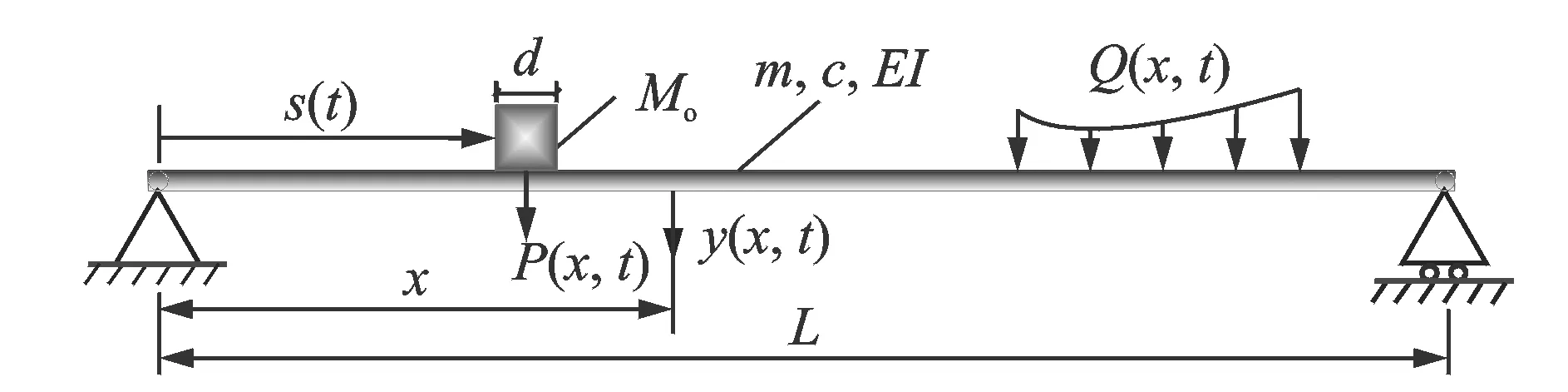
图1 移动质量-梁耦合系统Fig.1 Coupled moving-mass and beam system

其中：L，m，c和EI分别为梁的长度、单位长度质量、黏性阻尼系数和弯曲刚度；y(x,t)为梁上x处在t时刻的挠度；Q(x,t)为横向载荷；P(x,t)为移动质量对梁的等效作用力。

当移动质量的轴向尺寸d远小于梁的长度L时，忽略其转动惯性[12]，则移动质量对梁的等效作用力可写为

χ(s(t))δ(x-s(t))

(2)

其中：M0为移动质量的质量；g为重力加速度；s(t)为移动质量的位移函数；δ(x-s(t))为Diracdelta函数。

χ(s(t))为窗函数，定义为

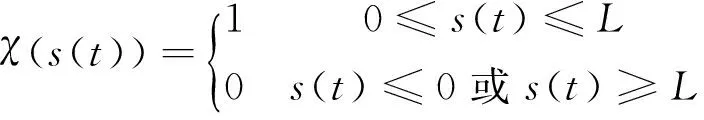
(3)

对于梁的挠度有

(4)

式(4)中各项依次表示牵连加速度、加速度法向分量、科氏加速度和向心加速度。

将式(2)和式(4)代入式(1)可得

(5)

其中：符号′表示对x的微分；符号·表示对t的微分。

设梁的挠度函数具有如下形式

(6)

其中：φi(x)(i=1,2,…，N)为梁的第i阶模态振型函数。

梁的挠度函数满足如下正交关系

(7)

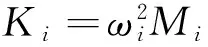
将式(6)代入式(5)可得

(8)

将式(8)两端同时乘以φj(x)，并沿[0,L]积分，利用模态振型函数的正交性可得

(9)

进一步，移动质量-梁耦合系统振动微分方程的矩阵形式可写为

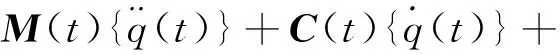
K(t){q(t)}={F(t)}

(10)

其中

M(t)=diag{Mi}+M0diag{φi(s)}Φ(s)

(11)

其中：Φ(s)为梁的模态振型函数矩阵；Φ′(s)和Φ″(s)分别为Φ(s)关于移动质量位移s的一阶和二阶导数矩阵。

由式(10)可知，移动质量-梁耦合系统为时变系统。

需要注意的是，上述推导过程中对梁的边界条件未加任何限制，只要梁的模态振型函数已知就可以应用该动力学模型进行分析，且在移动质量对梁作用力的等效过程中，仅忽略了移动质量的转动惯性，建模精度更高，适用范围更广。对于两端简支梁，模态振型函数为

(12)

2 数值仿真

移动质量-梁耦合时变系统的质量、阻尼和刚度矩阵均随移动质量的位置变化而变化，而移动质量的速度会影响阻尼和刚度矩阵，加速度只对刚度矩阵有影响。因此，通过数值仿真可分析移动质量运动形式对耦合时变系统模态参数的影响。

对于移动质量简支梁耦合时变系统，梁的长度为L=2 m，单位长度质量为m=4.71 kg/m，弯曲刚度为EI=1 050 N·m2、粘性阻尼系数假设为c=0。移动质量块的质量为M0=4.865 8 kg，运动形式为匀变速，即s(t)=v0t+at2/2，其中，v0为初速度，a为加速度，重力加速度取为g=9.8 m/s2。

2.1 速度对模态参数的影响

在加速度a=0，初速度分别为v01=0.05 m/s，v02=0.10 m/s和v03=0.20 m/s的情况下对质量块从简支梁一端运动到另一端的过程进行仿真，仿真时间分别为40,20和10 s。三种运动形式下，移动质量速度对耦合时变系统前4阶模态参数的影响如图2所示(横坐标表示质量块在简支梁上的位置)。

由图2可知， 移动质量的速度对耦合时变系统固有频率的影响很小，对模态阻尼比影响较大，且影响程度随移动质量速度的增大而增大。由于简支梁两端边界条件的对称性，移动质量匀速通过简支梁的过程中，耦合时变系统模态参数的变化规律也具有对称性。

2.2 加速度对模态参数的影响

在初速度v0=0.05 m/s，加速度分别为a1=0,a2=0.005 m/s2和a3=0.03 m/s2的情况下对质量块从简支梁一端运动到另一端的过程进行仿真，仿真时间分别为40,20和10s，在3种运动形式下，移动质量加速度对耦合时变系统前4阶模态参数的影响如图3所示(横坐标表示质量块在简支梁上的位置)。

图2 移动质量速度对模态参数的影响Fig.2 Modal parameters influenced by moving-mass velocity

图3 移动质量加速度对模态参数的影响Fig.3 Modal parameters influenced by moving-mass acceleration

由图3可知，移动质量的加速度对耦合时变系统固有频率的影响很小，对模态阻尼比影响较大，且影响程度随移动质量加速度的增大而增大。需要说明的是，当移动质量作匀加速运动时，其速度随时间的增加而增大，因而，模态参数的变化会受到速度与加速度的综合影响，且变化规律不再具有对称性。

综上可知，移动质量简支梁耦合时变系统的固有频率受移动质量运动速度及加速度的影响很小，模态阻尼比对移动质量的速度及加速度则较为敏感。在数值仿真中，系统自身的粘性阻尼系数均假设为c=0，因此，仿真得到的阻尼可认为是由移动质量诱导产生的附加阻尼。由图2和图3可知，附加阻尼可能为负值，因而，当系统自身阻尼较小时，附加阻尼效应可能导致系统的某一阶或某几阶模态阻尼比为负值。

3 实验系统设计

移动质量简支梁实验系统包括时变结构、激励系统、力和运动传感器、测量与分析系统、电机系统和支撑台体6部分，其设计方案及实物如图4所示。

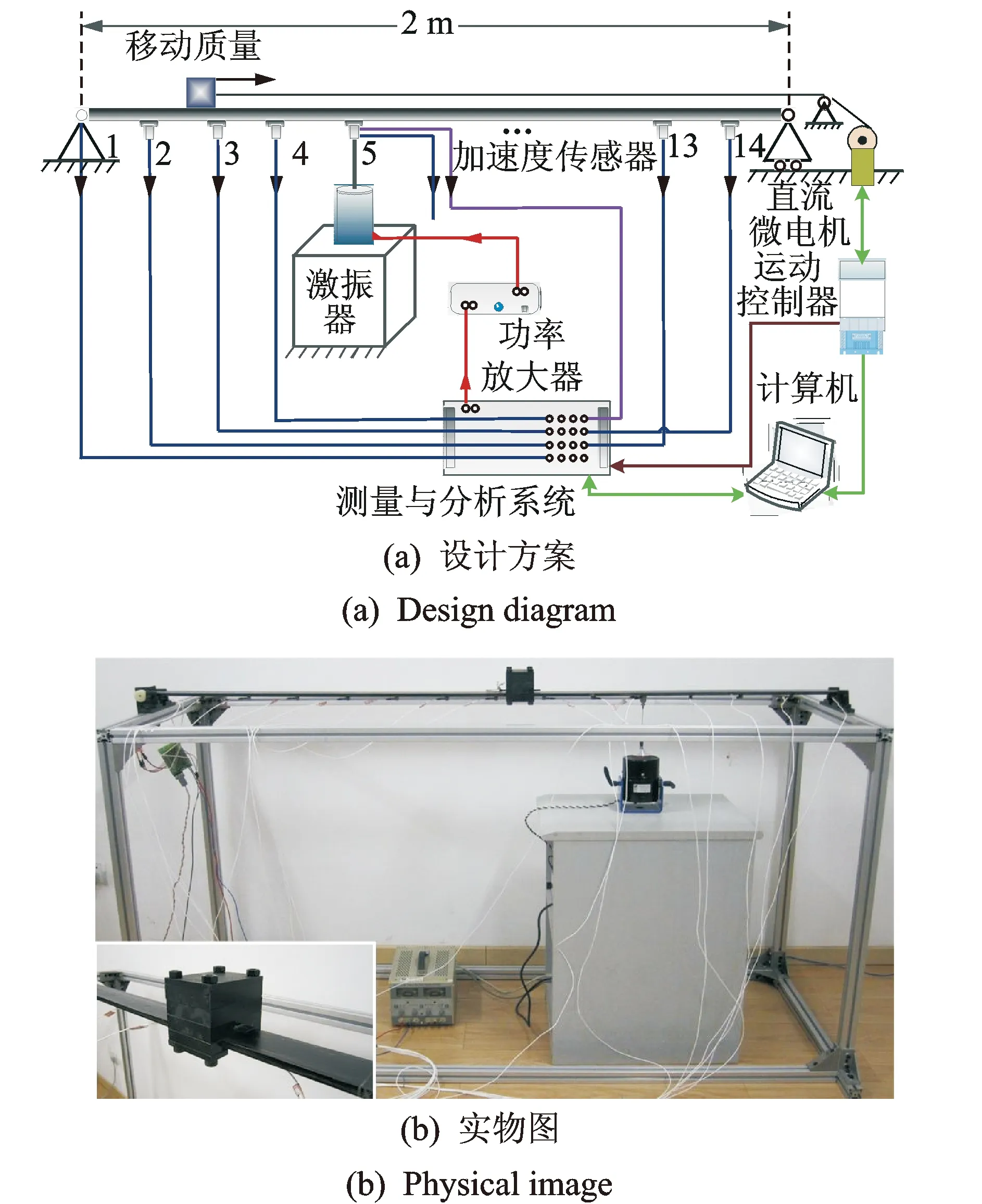
图4 移动质量简支梁实验系统设计方案及实物图Fig.4 Experimental system of the moving-mass and simply supported beam

时变结构包括简支梁和移动质量块，通过改变质量块的质量大小、运动形式(位置、速度和加速度)等方式来模拟不同时变特性的时变结构。简支梁为2 000mm×60mm×10mm(长×宽×高)的钢质梁，移动质量块的质量变化范围为2.080 0～4.865 8kg。

激励系统包括激振器和功率放大器，激振器用于输出不同类型的带宽信号或者单频信号，功率放大器用于对输出信号的幅值进行调节。实验系统中，激振器选用ModalShop2025E轻型模态激振器，功率放大器选用SmartAmpTM的2100E21-400功率放大器。

力和运动传感器分别用来测量时变结构所受到的激励信号和该激励作用下结构的动力学响应信号。力传感器选用PCBTM的288D01机械阻抗传感器，运动传感器选用PCBTM的333B30加速度传感器。

测量与分析系统选用LMSTM的SCADASIII系统，可用于预设力和运动传感器的采样频率和采样时间，并对传感器采集到的激励信号和结构动力学响应信号进行处理。

电机系统包括电机、编码器、运动控制器和同步绕线器，分别选用FaulhaberTM的2642W024CR直流微电机、IE2-512电磁编码器、MCDC3003S运动控制器和塑制同步绕线器。编码器和运动控制器用来控制电机输出端的运动形式(位置、速度和加速度)，电机输出端直接与同步绕线器固连，以绕线的方式驱动质量块在简支梁上移动。电机、编码器和运动控制器构成闭合回路，能够对电机输出端的运动形式进行精确控制，进而实现对质量块运动形式(位置、速度和加速度)的精确控制。此外，通过电机系统可预设力和运动传感器采样开始时刻质量块所需满足的运动信息标准，移动过程中，当质量块的运动信息满足该预设运动信息标准时，测量与分析系统启动力和运动传感器开始采样，采样终止时刻则通过测量与分析系统直接预设，实现了质量块任意运动形式下任意时间段内激励信号和结构动力学响应信号的采集。

支撑台体由金属型材搭建而成，为时变结构中的简支梁提供两端简支的边界条件。

4 实验结果

实验前，在简支梁下表面沿轴向均匀布置15个传感器，自左向右依次编号为1～15，如图4(a)所示。5号传感器位置为激励的施加位置，选用机械阻抗传感器同时测量该处的激励力和加速度响应信号；其余14个传感器均为加速度传感器，用以测量所在位置的加速度响应信号。

4.1 参考实验

对于移动质量简支梁实验系统，把从简支梁中点到其右侧与中点相距0.8m的区间做80等分，自左向右分别将质量块置放于等分点处，依次进行81组时不变结构动力学实验。实验过程中，M0=4.865 8 kg，激励为0～256Hz的随机激励，激励力和加速度响应信号的采样频率均为512Hz，采样时间为4s，选用H1估计[3](平均次数：30次)得到所有响应点与参考点(5号点)之间频响函数随质量块位置的变化规律，其中，5号响应点的原点频响函数如图5所示。

图5 原点频响函数随质量块位置的变化规律Fig.5 Driving-point frequency response function varying with mass position

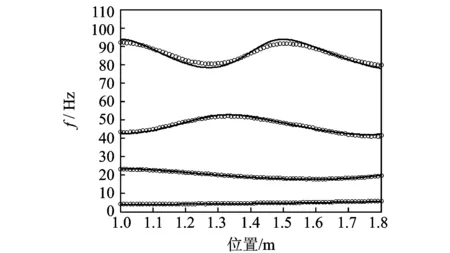
图6 固有频率随质量块位置的变化规律Fig.6 Natural frequencies varying with mass position

采用最小二乘复频域法[3](leastsquarescomplexfrequencydomain，简称LSCFD)辨识得到实验系统前4阶固有频率随质量块位置的变化规律如图6所示(圆圈表示辨识结果， 实线表示只考虑实验系统质量矩阵受移动质量位移影响而忽略其速度及加速度影响的无阻尼固有频率仿真结果)，前4阶模态阻尼比随质量块位置的变化规律如图7所示。

由图6可知，动力学模型与实验系统在固有频率上能够较好地吻合， 验证了动力学模型对于移动质量问题的适用性。图7中阻尼的辨识结果可作为质量块通过简支梁过程中耦合时变系统的初始阻尼，综合考虑初始阻尼与附加阻尼可得到质量块通过简支梁过程中实验系统的真实阻尼。

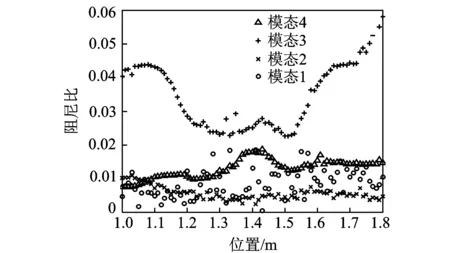
图7 模态阻尼比随质量块位置的变化规律Fig.7 Modal damping ratio varying with mass position

4.2 时变结构动力学实验

为对数值仿真结果进行验证，研究移动质量速度对系统模态参数的影响，进行如下三组时变结构动力学实验：质量块的运动形式依次为0.05，0.10和0.20m/s的匀速运动， 对应的采样时间依次为16，8和4s，每组实验均进行50次。实验过程中M0=4.865 8 kg，力和运动传感器的采样开始时刻为质量块通过简支梁中点的时刻，采样频率为512Hz。

4.2.1 频域辨识结果

由于结构特性随时间的变化，时变结构的响应信号具有非平稳性，传统的基于傅里叶变换的谱分析已无法反映非平稳信号频率分量的时间变换特征，可通过时频分析[14-15]的方法获取响应信号随时间变化的频谱。采用平滑伪魏格纳-维尔分布(smoothedpseudoWigner-Villedistribution[16]，简称SPWVD)对时变结构的加速度响应信号进行时频分析，估计出移动质量三种不同速度下各响应点处加速度响应信号时间相关自功率谱的平均值，如图8所示。由图8(a～c)可知，加速度响应信号的时间相关自功率谱中的“脊线”能够清晰地指示出实验系统固有频率的变化趋势。根据加速度响应信号的时间相关自功率谱， 采用基于时频分布系数的加权最小二乘方法[17]对实验系统的固有频率进行辨识，辨识结果如图8(d～f)所示(圆圈表示辨识结果，实线表示仿真结果)。比较图8(d～f)中辨识结果与仿真结果可得，所选用频域方法能够准确地辨识得到实验系统的前4阶固有频率。

4.2.2 时域辨识结果

对于移动质量简支梁实验系统，如将阻尼比高于8%[3]或负阻尼的极点作为数学极点直接滤掉将导致固有频率的辨识结果失真。考虑到移动质量诱导产生的附加阻尼，文中将-1%<ξ<5%作为阻尼比估计值的筛选区间，将阻尼比位于区间内的极点作为物理极点加以保留，而将阻尼比位于区间外的极点作为数学极点直接滤掉。

采用泛函序列-多分量时变自回归滑动平均(functionalseriesvectortime-dependentautoregressivemovingaverage，简称FS-VTARMA)[18]方法对实验系统的固有频率进行辨识。对于每组实验，分别基于50次实验数据进行辨识，将满足筛选条件的固有频率辨识结果进行统计，刻画出实验系统固有频率的变化趋势，如图8(g～i)所示(圆圈表示辨识结果，虚线表示仿真结果)。比较图8(g～i)中辨识结果与仿真结果可得，所选用时域方法无法辨识出移动质量简支梁实验系统的第1阶固有频率，且辨识精度依赖于采集数据的长度，采集数据越长，辨识精度越高。

5 结 论

1) 在仅忽略移动质量转动惯性的前提下，建立了任意激励下移动质量-梁耦合时变系统的动力学模型，精度更高，适用范围更广。基于该动力学模型，可分析移动质量速度与加速度对耦合时变系统模态参数的影响，得到移动质量诱导产生的附加阻尼，对实际工程结构的设计具有指导意义。

2) 移动质量简支梁实验系统中质量块的质量大小可调，运动形式精确可控，实现了质量块任意运动形式下任意时间段内激励信号和结构动力学响应信号的采集，能够模拟不同时变特性的时变结构，物理意义明确，时变特征明显，可用于时变结构模态参数辨识方法的实验验证。

图8 加速度响应信号的时间相关自功率谱及固有频率辨识结果Fig.8 Time-dependent auto power spectral of acceleration signals and estimated results of natural frequencies

3) 频域和时域两种方法辨识结果表明，移动质量简支梁实验系统具有良好的可观测性，系统响应自由度的选择十分方便，且研究该系统动态特性所需要的全部数据都是可以测量的。

4) 现有已公开的模态参数辨识方法尚不能准确地辨识出随机激励下该实验系统的阻尼特性用于相关建模理论的研究，因此笔者未给出阻尼的辨识结果。然而结合所建动力学模型，提出的实验系统可为阻尼辨识方法的进一步研究提供实验验证。

[1] Au F T K, Jiang R J, Cheung Y K. Parameter identification of vehicles moving on continuous bridges[J]. Journal of Sound and Vibration, 2004, 269(1-2): 91-111.

[2] Marchesiello S, Bedaoui S, Garibaldi L, et al. Time-dependent identification of a bridge-like structure with crossing loads[J]. Mechanical Systems and Signal Processing, 2009, 23(6): 2019-2028.

[3] Heylen W, Lammens S, Sas P. Modal analysis theory and testing[M]. Leuven: Katholieke Universiteit Leuven, 2007: A1.1-A3.34，B4.11.

[4] Poulimenos A G, Fassois S D. Output-only stochastic identification of a time-varying structure via functional series TARMA models[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1180-1204.

[5] Spiridonakos M D, Fassois S D. An FS-TARbased method for vibration-response-based fault diagnosis in stochastic time-varying structures: experimental application to a pick-and-place mechanism[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 206-222.

[6] Liu K, Deng L. Identification of pseudo-natural frequencies of an axially moving cantilever beam using a subspace-based algorithm[J]. Mechanical Systems and Signal Processing, 2006, 20(1): 94-113.

[7] 续秀忠. 时变线性结构模态参数识别的理论及实验研究[D]. 上海：上海交通大学, 2003.

[8] Biondi B, Muscolino G. New improved series expansion for solving the moving oscillator problem[J]. Journal of Sound and Vibration, 2005, 281(1-2): 99-117.

[9] 胡红生, 钱苏翔. 移动质量激励下梁动态响应分析与试验研究[J]. 振动、测试与诊断, 2010, 30(2): 153-157.

Hu Hongsheng, Qian Suxiang. Test and dynamic response analysis of beam under a moving mass[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 153-157. (in Chinese)

[10]王文亮, 杜作润. 结构振动与动态子结构方法[M]. 上海: 复旦大学出版社, 1985:114-119.

[11]Michaltsos G T, Sophianopoulos D, Kounadis A N. The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J]. Journal of Sound and Vibration, 1996, 191(3): 357-362.

[12]Michaltsos G T. The influence of centripetal and coriolis forces on the dynamic response of light bridges under moving vehicles[J]. Journal of Sound and Vibration, 2001, 247(2): 261-277.

[13]Michaltsos G T. Dynamic behaviour of a single-span beam subjected to loads moving with variable speeds[J]. Journal of Sound and Vibration, 2002, 258(2): 359-372.

[14]Cohen L. Time-frequency analysis[M]. New Jersay: Prentice Hall, 1995:70-81.

[15]Qian S. Introduction to time-frequency and wavelet transforms[M]. New Jersay: Prentice Hall, 2002: 147-198.

[16]Feng Zhipeng, Liang Ming, Chu Fulei. Recent advances in time-trequency analysis methods for machinery fault diagnosis: areview with application examples[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 165-205.

[17]周思达. 线性时变结构时频域模态参数辨识理论及实验研究[D]. 北京:北京理工大学, 2012.

[18]Spiridonakos M D, Fassois S D. Parametric identification of a time-varying structure based on vector vibration response measurements[J]. Mechanical Systems and Signal Processing, 2009, 23(6): 2029-2048.

10.16450/j.cnki.issn.1004-6801.2015.05.018

*北京理工大学研究生科技创新专项计划资助项目;北京理工大学基础研究基金资助项目(20120142009)

2013-11-18；

2014-03-18

O327

马志赛，男，1988年6月生，博士生。主要研究方向为时变系统模态参数辨识。 E-mail：mazhisai2008@163.com 通信作者简介：刘莉，女，1964年5月生，博士、教授。主要研究方向为飞行器总体设计、飞行器结构分析与设计、飞行动力学与控制等。 E-mail:liuli@bit.edu.cn