基于非线性退化模型的加速度计寿命评估*
李 瑞, 汪立新, 周志杰, 赵曦晶
(第二炮兵工程大学控制工程系 西安,710025)
基于非线性退化模型的加速度计寿命评估*
李 瑞, 汪立新, 周志杰, 赵曦晶
(第二炮兵工程大学控制工程系 西安,710025)
针对传统性能退化模型难以对退化轨迹为非线性的设备进行有效寿命评估的问题,首先,建立了一种基于扩散过程的非线性模型,并将推导其失效阈值首达时间分布的问题转化为推导标准布朗运动失效阈值首达时间分布的问题,得到了首达时间意义下的近似寿命分布;然后,提出了该模型未知参数的极大似然函数估计方法;最后,使用此模型评估分析了一组加速度计的寿命,并与传统退化模型进行比对分析。实验结果证明了模型的评估结果更为准确有效。
加速度计; 非线性; 退化过程; 寿命
引 言
作为飞行器惯导系统的核心部件,加速度计的健康状态评价,主要取决于其标度因数的稳定性。在实际使用中,加速度计的传感器、伺服电路及力矩组件等精密部件的性能随工作时间而逐渐变化,最终影响输出精度。同时,加速度计的性能也会因为工作环境(温度、湿度)的变化而逐渐退化[1-2]。因此,有效评估加速度计寿命,对提高飞行器的安全性有着重要作用。
传统的可靠性及寿命分析方法常基于历史寿 命数据,但对于高可靠性或贵重设备而言,该方法存在时效差和成本较高的不足。针对该问题,基于性能退化的分析方法被引入,在设备性能随时间退化积累到一定程度并最终导致设备失效(退化型失效)的过程中,性能参数随时间退化的数据(性能退化数据)同样含有可靠性信息,因此利用性能退化数据建立设备性能退化模型来刻画失效过程是一种可行的方法。当前,基于退化数据的方法已成为设备可靠性及寿命分析的重要途径之一[3-4]。
1990年,Nelson[5]总结了90年代以前的退化建模方法。Lu等[6]在1993年首次使用随机系数回归模型来描述退化过程。Meeker等[7]则使用极大似然分析法来处理退化数据。一般文献都将退化模型的参数假设为固定参数或是服从某种分布的随机变量,这意味着某一确定设备的退化过程参数一旦确定,其退化轨迹随之固定,忽视了退化过程的不确定性。因此,有学者建议使用随机过程来体现退化过程中的随机性与动态性[8]。目前,常见的用随机过程描述的性能退化模型常有两种假定[3]:a.退化过程单调不可逆;b.退化轨迹是线性或是可以变换为线性的。这种假设有时在某些情况下无法满足,因为:a.设备性能常因外部环境、内部动态结构等因素呈现不确定性,不能保证退化过程的单调性;b.复杂设备在性能退化过程中,各内部组件的性能退化规律不一致,且某些组件的退化轨迹本身就是非线性的,因而设备性能退化轨迹不能确保服从线性规律。因此,对于具有非线性退化过程的设备,使用具有非线性特征的随机过程来描述其退化模型能更有效地评估其可靠性及寿命。
针对摆式加速度计标度因数随工作时间增长而变化加剧且不稳定,有时退化轨迹不严格服从线性规律的问题,笔者建立了一种非线性扩散退化过程模型,将转化为标准Brownian运动的首达时间概率密度,得到设备在首达时间意义下的寿命及可靠度。
1 非线性性能退化模型
基于在性能退化过程中设备的输出并不总是一精确稳定值这一工程现象,扩散过程自然地成为了描述设备性能退化的选择[9]。扩散过程类似于Wiener过程,但其漂移系数与扩散系数不再限于常数。许多情况下,由于噪声和扰动的介入,设备的真实退化过程难以精确测量,而真实的扩散过程也无法直接测得,两者虽然都无法直接测得,但却都是由一定的趋势驱动的,因此从这个出发点考虑,用扩散过程来描述具有连续波动且不可精确测量的退化过程具有可行性。利用非线性模型能更好地复现具有非线性退化特征的设备性能衰退过程,同时考虑到许多设备在实际测量中的性质较符合扩散过程,描述设备性能非线性退化过程的模型为
(1)
其中:Y(t)是由标准Brownian运动b(t)驱动的退化过程;a(t,α,β)为漂移系数,这里a(t,α,β)为时间的非线性函数;σb为扩散系数。
在描述某一类设备的性能退化过程时,需考虑到:首先,该类设备因为构造的差异,其性能退化过程会不同于其他种类的设备,因此在退化模型中需有一个参数反映这种差别;其次,即使同类型、同批次的设备,由于内部组件的微小差异,也将导致其性能退化过程有所不同。所以,这里使用随机参数α来反映同类设备间的个体差异,用固定参数β反映某类设备的退化特性。
漂移系数a(t,α,β)的具体形式,一般根据性能退化轨迹来寻找合适的函数。笔者对以Wiener过程为基础的线性退化模型进行拓展,令a(t,α,β)=αβtβ-1,当β=1时,式(1)变形为Wiener过程;当β≠1时,式(1)为非线性退化过程;因此,模型在处理退化数据时更有灵活性,可以同时处理线性及具有指数特征的退化数据。
2 寿命估计及可靠性分析
在进行寿命估计之前,需要给出寿命T的定义。在以往的文献中,常将寿命定义为
T={t:Y(t)≥w}
(2)
其中:w为失效阈值。
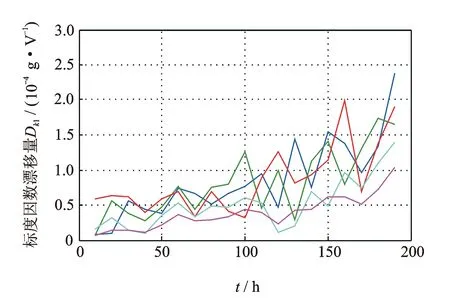
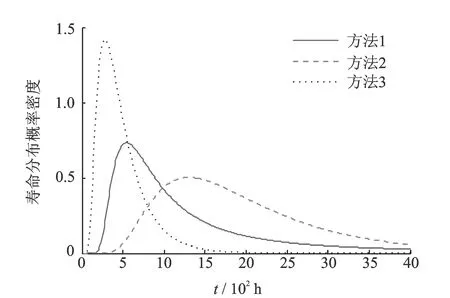
当性能退化过程单调时这种定义是明确的,但是在引入随机过程后,设备性能退化过程无法满足单调的假设,此时可能出现t1 T=inf{t:Y(t)≥w} (3) 即将寿命定义为退化过程Y(t)首次到达阈值w的时间(简称首达时间)。 当引入扩散过程后,对非线性退化过程进行寿命分析的难点在于如何求得Y(t)首达时间的概率密度函数。将Y(t)转换成某种易求得首达时间概率密度函数的随机过程,是一种解决该问题的途径。Ricciardi[12]提出了如下理论。 对于漂移系数为μ(x,t),扩散系数为σ(x,t)的扩散过程X(t),令c1(t)和c2(t)为任意的时间函数,则当漂移系数μ(x,t)可以写为 (4) 则存在 (5) (6) 可以将扩散过程描述的X(t)变换为标准Brownian运动。其中:z为X(t)中的任意值;ti∈[0,∞)(i=0,1,2);k1,k2,k3均为任意常数,k1>0。 根据以上理论,可将式(1)中的扩散过程变换为标准Brownian运动,变换过程如下。 首先,令Y(0)=0,于是有t0=0和z=0。同时,设k1=1,k2=k3=0。 (7) (8) (9) (10) (11) (12) (13) 根据以上的分析和假设,将式(10)和式(13)代入式(12)中,得到 (14) 漂移系数中的参数α是一个随机参数,它反映了同类同批次设备个体间的差异。一般来讲α~N(μα,σα),所以利用全概率公式,由式(14)可得 (15) (16) 将式(16)代入式(15),得到扩散过程Y(t)的首达时间的近似概率密度函数fT(t)为 (17) 寿命的期望ET和可靠度函数计算式分别为 (18) (19) 假设有个N个待测设备,分别在t1,t2,…,tm时刻同时对待测设备测量。因此,第i个设备在tj时刻的性能指标可表示为 (20) (21) 由于不同待测设备测量值之间相互独立,于是对未知参数Θ=(μα,σα,σb,β)的对数似然函数可表示为 (22) (23) L(Θ|Y)分别对μα和σα求偏导数,得 (24) (25) 令式(24)和式(25)为零,得到μα和σα的极大似然表达式为 (26) (27) 将式(26)和式(27)代入式(22)中,得到关于σb和β的极大似然函数为 (28) 笔者将对20世纪90年代初期引入我国的一组宝石轴承加速度计寿命进行分析。该批次加速度计引入后每月工作3次,每次通电时长约1 h,至今已累计约有700 h的工作时间。厂家给定的平均失效时间为1 400 h,但现已有部分产品已出现失效现象,为评估该产品的实际寿命情况,这里对一组未启封的产品进行寿命分析,以提供参考。 该类型加速度计由摆组件、信号传感器、直流力矩器和宝石支撑等主要部件构成。在长时间通电工作后,此类加速度计的信号传感器与直流力矩器由于长期发热的影响,组件性能会逐渐发生变化[15],从而导致加速度计的系统性能下降。为衡量加速度计的性能表现,选取对输出误差影响较大的一次项标度因数K1进行评估。 为构建测试系统,笔者选用中国船舶工业集团第六三五四研究所研制的2WT-500型双轴带温控箱速率位置转台(其回转角精度为±1.5″,双轴定位精度为±3″)和惠普公司的34401A型万用表构成测试平台,并用Labview搭建软件系统。在测试系统构建好后,选取5套加速度计,共测试20次,各套加速度计的测量时刻相同。每次通电10h,取所采集数据的平均值。相邻两次测试间停机休息5h,以避免因长时间连续工作而导致的加速度计性能异常。5套加速度计均以第1次测试的K1为基准点,计算其余19次测试的相对漂移Dk1,失效阈值w=0.001。其漂移数据如表1所示。 表1 标度因数K1漂移量 图1 标度因数漂移量Dk1Fig.1 Drift of scale factorDk1 图2 加速度计寿命分布概率密度函数Fig.2 PDF of accelerometer′s life time 从表2 中可以看到,采用笔者方法分析得到该型加速度计的平均失效寿命为1 539h左右,较其他两种方法更与厂家额定的数据相近。同时,模型拟合残差的均方差(meansquarederror,简称MSE)反映出笔者方法与实际数据的拟合程度更好。在图2中,由方法1得到寿命概率密度函数在700h左右达到峰值,设备出现失效现象的概率较高,这在实际情况中也有体现。以上几点表明了笔者提出的方法能较好地反映加速度计的寿命情况。但应该注意到,一是由于样本量小的限制,二是由于算法得到的概率密度函数是近似值,所以分析结果存在一定风险(这一点从概率密度函数分布相对发散可看出)。为了解决该问题,首先通过获取更多的数据进行数据更新,然后在分析数据前减小噪声干扰,使结果逼近真实情况。 表2 加速度计寿命期望及相关参数 图3 加速度计可靠度Fig.3 Reliability of accelerometer 为解决对加速度计进行寿命预测与可靠性评估时无法对非线性退化轨迹准确描述的问题,建立了一种非线性扩散退化过程模型,将其首达时间分布概率密度转化为标准Brownian运动首达时间概率密度,从而找到了其近似寿命分布函数,并通过一组加速度计的测试数据验证了其有效性。由于三维搜索的计算量远超二维搜索,因此在参数识别时要求不同设备的测试时刻要保持一致,同时这样也有助于提高参数估计值的准确度。 [1] 袁宏杰, 李楼德, 段刚, 等. 加速度计贮存寿命与可靠性的步进应力加速退化试验评估方法[J]. 中国惯性技术学报,2012, 20(1): 113-116. Yuan Hongjie, Li Loude, Duan Gang, et al. Stor- age life and reliability evaluation of accelerometer by step stress accelerated degradation testing[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 113-116.(in Chinese) [2] 李新蕾, 任吉林, 任尚坤, 等.铁磁构建残余寿命评估方法[J].航空学报,2010,31(10):2109-2114. Li Xinlei, Ren Jiling, Ren Shangkun, et al. Residual life assessment of ferromagnetic components[J]. Acta Aeronautica et Astronautica Sinica,2010, 31(10): 2109-2114. (in Chinese) [3] Si Xiaosheng, Wang Wenbin, Hu Changhua, et al. Remaining useful life estimation-A review on the statistical data driven approaches[J]. European Journal of Operational Research, 2011, 213(1): 1-14. [4] 李晓阳, 姜同敏. 基于加速退化模型的卫星组件寿命与可靠性评估方法[J].航空学报,2007,28(S):1640-1643. Li Xiaoyang, Jiang Tongmin. Constant-stress accelerated degradation testing of satellite assemblies[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(S): 1640-1643. (in Chinese) [5] Nelson W. Accelerated testing: statistical models, test plans and data analyses[M]. New York: Wiley, 1990:51-107. [6] Lu C J, Meeker W Q. Using degradation measures to estimate a time-to-failure distribution[J]. Technometrics, 1993, 35(6): 543-559. [7] Meeker W Q, Escobar L A. Statistical Methods for Reliability Data[M]. New York:John Wiley & Sons, 1998:27-36. [8] Aalen O O, Borgan O, Gjessing H K. Survival and event history analysis: A process point of view[M]. New York:Springer, 2008:301-346. [9] Si Xiaosheng, Wang Wenbin, Hu Changhua, et al. Remaining useful life estimation based on a nonlinear diffusion degradation process[J]. IEEE Transactions on Reliability, 2012, 61(1): 50-67. [10]Aalen O O, Gjessing H K. Understanding the shape of the hazard rate: A process point of view (with discussion) [J]. Statistical Science, 2001, 16(1):1-22. [11]Ting Lee M-L, Whitmore G A. Threshold regression for survival analysis: Modeling event times by a stochastic process reaching a boundary[J]. Statistical Science, 2006, 21(4): 501-513. [12]Ricciardi L M. On the transformation of diffusion processes into the Wiener process[J]. Journal of Mathematical Analysis and Applications, 1976, 54: 185-199. [13]Cox D R, Miller H D. The Theory of Stochastic Processes[M]. London: Methuen and Company, 1965:137-155. [14]Durbin J. The first-passage density of a continuous Gaussian process to a general boundary[J]. Journal of Applied Probability,1985,22 (1): 99-122. [15]王广林, 刘斯尧, 王杰, 等. 高精度弹性元件疲劳寿命试验系统[J].振动、测试与诊断,2011,31(5):548-551. Wang Guanlin, Liu Shiyao, Wang Jie, et al. Fatigue life test system for high-precision elastic component[J].Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 548-551. (in Chinese) [16]Tseng S T , Peng C Y. Optimal burn-in policy by using an integrated Wiener process[J]. Institude of Industrial Engineers Transactions,2004,36(2004):1161-1170. 10.16450/j.cnki.issn.1004-6801.2015.05.009 *国家自然科学基金资助项目(61174030);二炮装备技术基础基金资助项目(EP114054) 2013-09-01; 2013-12-18 U666.1 李瑞,男,1984年6月生,博士生。主要研究方向为惯性敏感器件的可靠性分析及维护。曾发表《基于加速退化模型的加速度计非线性特征分析及贮存寿命预测》(《中国惯性技术学报》2014年第22卷第1期)等论文。 E-mail:lr_zeskr@163.com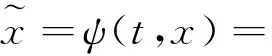
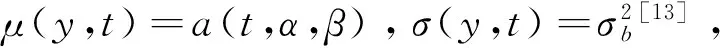
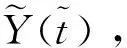
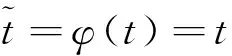
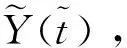
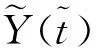

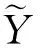
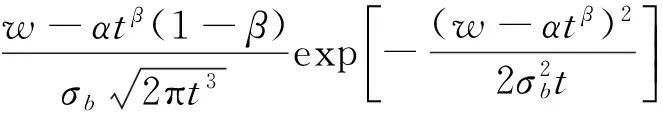

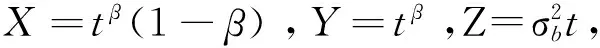


3 参数估计
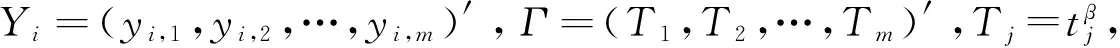


4 加速度计寿命与可靠性评估

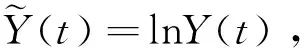


5 结束语


