基于LMD能量特征的滚动轴承故障诊断方法*

石瑞敏， 杨兆建

(太原理工大学机械工程学院 太原，030024)



基于LMD能量特征的滚动轴承故障诊断方法*

石瑞敏， 杨兆建

(太原理工大学机械工程学院 太原，030024)

针对滚动轴承故障振动信号的多载波多调制特性，提出一种基于局域均值分解(local mean decomposition, 简称LMD)能量特征的特征向量提取方法，并与支持向量机相结合用于滚动轴承的故障诊断。首先，采用LMD方法将复杂调制振动信号分解为若干单分量信号乘积函数(production function，简称PF)；然后，对反映信号主要特征的PF基于时间轴积分，得到各PF分量能量矩并构造特征向量；最后，将其输入多分类支持向量机中，用于区分滚动轴承的故障类型与故障程度。对滚动轴承内圈故障、外圈故障及滚动体故障振动信号的分析结果表明，该方法能有效提取滚动轴承各工作状态信号的故障特征，能准确识别故障类型，同时对故障程度的判断表现出较高的识别率。

滚动轴承； 局域均值分解； 能量特征； 故障诊断

引 言

滚动轴承是各种旋转机械中应用广泛的一种通用机械部件，在设备运行过程中起承受与传递载荷的作用，较之其他机械零件更容易发生磨损、点蚀及裂纹等缺陷与损伤，据统计仅有10%～20%的轴承达到设计寿命[1]。传统的轴承故障诊断方法大多是通过对轴承振动信号进行时域或频域分析，获取各轴承零部件故障特征频率，从而对轴承的工作状态进行辨识。随着现代信号处理技术的发展，小波分析、经验模态分解及局域均值分解等时频域分析方法运用到滚动轴承的故障诊断中，取得了良好的效果。张进等[2]提出一种时间-小波能量谱信号处理方法，更为有效地提取了信号特征微弱的滚动轴承内圈与滚珠故障。张志刚等[3]提出一种基于改进经验模态分解方法与谱峭度法的滚动轴承特征提取方法，对强噪声背景中瞬态冲击成分进行了有效度量和定位，获得了更为清晰的故障信息包络图。程军圣等[4]将局域均值分解方法与BP神经网络结合起来，有效用于滚动轴承故障类型的自动分类。

实际采集到的滚动轴承故障信号除包含损伤元件运转过程中的周期冲击成分之外，还包含受冲击激发的各元件固有频率振动，且其频率与幅值被脉动激发力调制，使得实际故障信号表现出多载波多调制的特性[5]；另外，由于受到轴与轴上多种零件振动的干扰激励表现出非平稳、非线性的特点。局域均值分解方法是由Smith[6]于2005年提出的一种自适应信号时频分析方法，它可将原始信号分解为若干个具有物理意义的瞬时频率的分量之和，分解过程由高频到低频依次分解，同时避免了经验模态分解方法存在的过包络与欠包络现象，适于非平稳非线性信号的处理。LMD方法将复杂的多分量调幅调频信号分解为单分量的调幅调频信号，且分解结果保持原信号的幅值与频率变化，因此LMD方法非常适合处理滚动轴承故障信号等非平稳非线性且多分量的调幅-调频信号[7]。笔者提出LMD能量特征与支持向量机(support vector machine，简称SVM)相结合的滚动轴承诊断方法。首先，采用LMD将振动信号进行分解，得到若干单分量的调幅-调频信号PF分量；然后，选取PF能量矩作为特征值，并构造相应特征向量输入支持向量机分类器中，实现区分滚动轴承工作状态与故障程度的目的。通过对滚动轴承正常状态、内外圈故障及滚动体故障的诊断结果分析表明，提出的基于LMD能量特征与SVM的诊断方法具有较高的诊断速率与识别率，可有效用于滚动轴承的典型故障诊断。

1 LMD方法

局域均值分解方法的本质是获得原始信号分离出的纯调频信息与包络信息，它将原始信号自适应地分解成若干个瞬时幅值有意义的乘积函数PF分量之和，任一PF分量均由一个包络信号和一个纯调频信号相乘而得，结合所有PF分量的瞬时幅值与瞬时频率便可获得原始信号完整的时频分布，对其分析可以更有效地从中提取振动信号所包含的反映工作状态与故障的特征信息[8]。

原始信号x(t)经LMD分解后，得到i个单分量调幅-调频信号PFi及1个单调的残余分量r(t)，即分解可完整地保留原始信号信息，将信号的时频分布体现在所有的PF分量的瞬时幅值与瞬时频率中。

2 基于LMD的滚动轴承故障特征提取

2.1 故障特征提取方法

因表面疲劳或应力集中而损伤的滚动轴承各元件，在运转过程中振动信号表现为周期性的冲击信号，该信号易受到脉动激发力的调制而表现出调幅-调频特征[9]。LMD方法能够将复杂的多分量调幅-调频信号自适应地分解为单分量的调幅-调频信号，同时又能完整保留原信号的幅值与频率信息，可提取滚动轴承振动信号中的故障特征。当滚动轴承元件发生故障时，振动信号在相同频带内信号能量会发生较大差别，能量分布在频带之间也会产生差异[4]，而LMD分解的PF分量包含了各个频段的信息，为了更好地捕捉到隐藏在信号中的故障信息，笔者提出一种基于PF能量矩的故障特征提取方法。

LMD方法将原始信号x(t)分解后表示为所有PF分量与残余分量r(t)之和，其中PF分量由瞬时幅值与纯调频信号相乘得到，由纯调频信号又可求得信号的瞬时频率。借鉴Hilbert-Huang变换思想，忽略残余分量，原始信号x(t)可以表示为瞬时幅值与瞬时频率的函数S(f,t)，即

其中：ei(t)和fi(t)分别为第i个PF分量的瞬时幅值与瞬时频率；n为PF分量个数。

根据这一时频分布表示形式，不仅可以计算信号的总能量，还可以计算信号在时频空间的局部能量，即

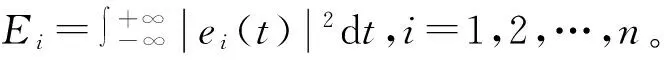
2.2 故障状态对能量矩的影响

本实验采用的数据来自于美国凯斯西储大学轴承实验数据[10]。试验台由电动机、扭矩传感器/译码器、测力计及电器控制装置组成。测试轴承选用电机输出端型号为6205-2RSSKF的深沟球轴承，将振动加速度传感器垂直固定于轴承上方，采集正常、内圈故障、外圈故障及滚动体故障的振动信号，采样频率为12 000Hz。各元件故障点为电火花加工单点损伤，损伤直径分别为0.177 8，0.355 6及0.533 4mm，由于外圈位置相对固定，考虑到损伤点相对于轴承负荷区位置对系统振动的影响，选择外圈损伤点布置于6点钟位置。电机负载由风机调节，测试负载分别为0，0.735 5，1.471 0及2.206 5kW，对应测试转速分别为1 797，1 772，1 750及1 730r/min。以某工况内圈故障信号为例，采用LMD方法进行分解，其分解结果如图1所示，可以看到多分量的复杂调幅-调频原始信号分解为5个单分量的调幅-调频PF分量及一个剩余分量，分解后各PF分量反映了信号各频段的不同特征。图2为分解所得PF分量对应的能量矩棒图，可见信号能量主要集中于高频分量，故文中后续处理选取前4个PF分量能量矩。

2.2.1 损伤程度对PF能量矩的影响

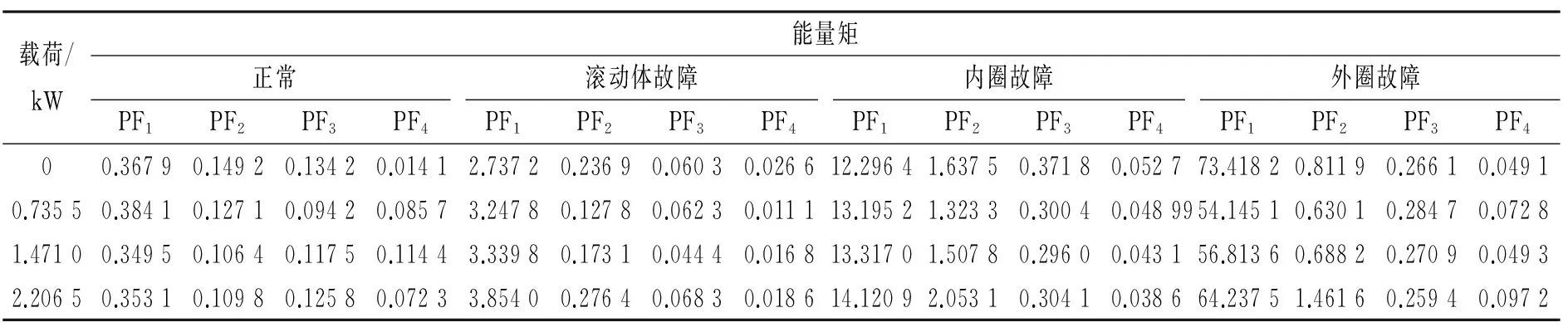
表1表示当载荷为0kW，转速为1 797r/min，损伤程度分别为0.177 8，0.355 6及0.533 4mm时，各故障状态轴承能量矩数据示例。通过对100组数据测试集的结果分析得出，对于同样损伤程度的不同故障，轴承外圈发生故障时，第一阶PF分量的能量矩最大，内圈故障次之，滚动体故障最小。各种损伤程度都呈现这一规律。当故障状态相同时，并不是损伤程度越大，能量矩值越大，且不同故障表现出不同的变化规律。对于滚动体故障，第1阶PF分量的能量矩随损伤程度增大而减小。对于内圈与外圈故障，在轻微损伤下能量矩较大；然后随着损伤程度加大，能量矩先变小；当损伤达到一定程度后，能量矩又变大，说明能量矩对轻微故障具有较高敏感度。

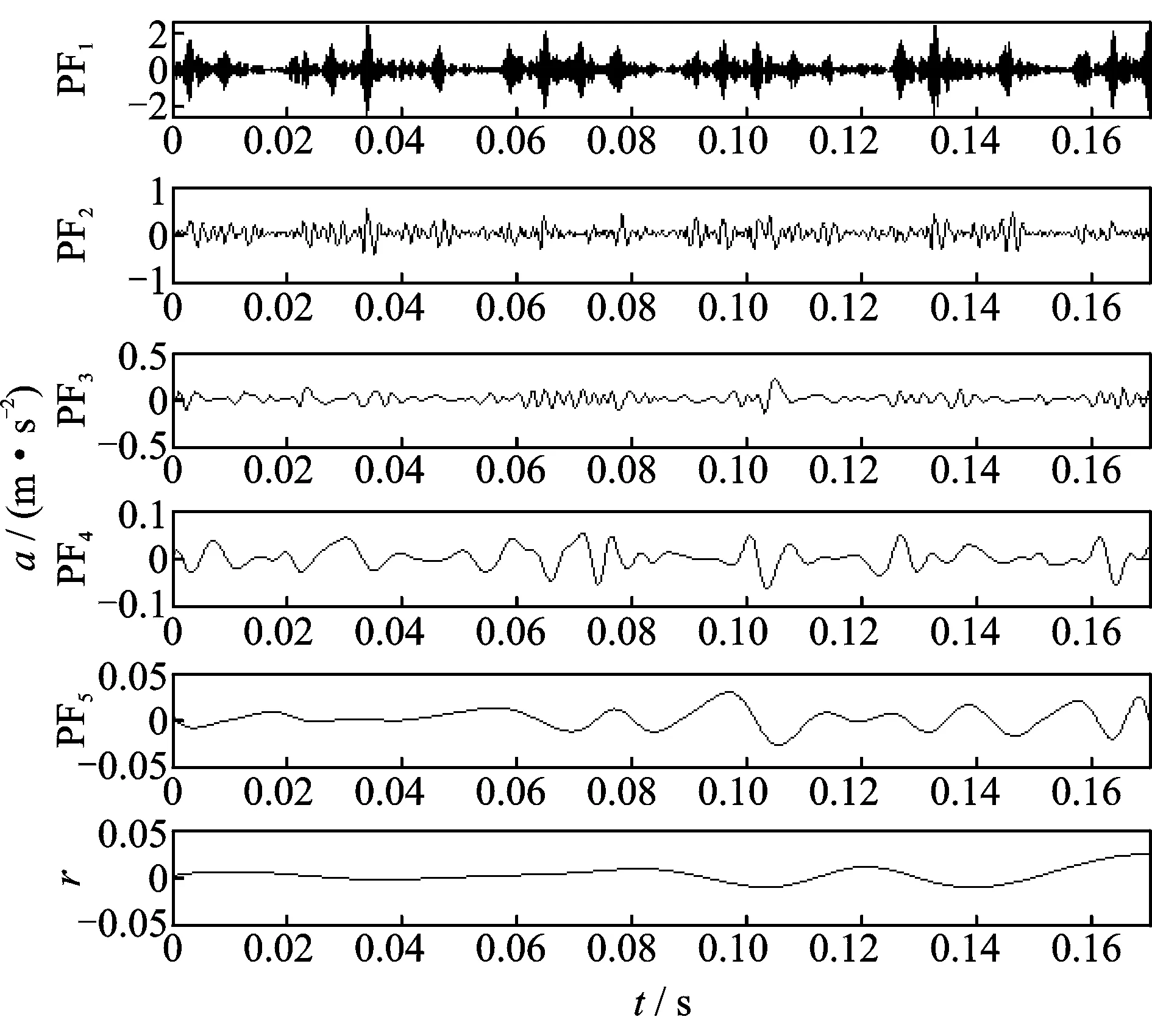
图1 内圈故障的滚动轴承振动信号LMD分解结果Fig.1 The LMD results of rolling bearing with inner-ring fault

图2 内圈故障的滚动轴承各阶PF分量能量矩Fig.2 The energy moment of PF of rolling bearing with inner-ring fault

2.2.2 载荷对PF能量矩的影响

取损伤程度为0.177 8mm，载荷分别为0，0.735 5，1.471 0及2.206 5kW的测试数据进行分析。轴承在不同载荷下LMD分解结果的能量矩示例如表2。100组测试数据集的数据显示，在同样载荷作用下，滚动轴承在正常运转、滚动体故障、内圈故障及外圈故障情况下，振动信号第1阶PF分量能量矩取值明显不同，当出现故障时，能量矩会明显增大，且外圈发生故障时其值最大，内圈故障次之，滚动体故障较小。对于同种故障而言，随着载荷的增大能量矩也变大，但是增大的数值较小，表现出较小的敏感性。

3 基于PF能量矩和SVM的滚动轴承故障诊断

LMD方法将原始信号自适应的在全部频带范围内依次分解，使得对于频带能量的分析更为合理。由于一定频段里的能量特征中包含着丰富的故障信息，各频带能量大小以及单频带能量占总能量比值等参数都作为特征值用于对滚动轴承工作状态的识别。传统的能量算法对故障信号的频率与故障有很好的识别能力，但是没有考虑各频带能量随时间t的分布情况。为进一步提高滚动轴承工作状态识别的准确性，笔者采用LMD方法对原始信号进行分解，提取分解后各PF分量的能量矩作为特征参数输入SVM，进而对滚动轴承的故障类型与程度进行分类识别。基于PF能量矩与SVM的滚动轴承故障诊断方法实现步骤如下。

表1 损伤程度对各阶PF分量能量矩的影响

Tab.1 The influence of damage degree on energy moment of PF

损伤程度/mm能量矩滚动体故障内圈故障外圈故障PF1PF2PF3PF4PF1PF2PF3PF4PF1PF2PF3PF40.17786.73720.23690.06030.0266812.29641.63750.37180.052773.41820.81190.26610.04910.35564.91680.21010.10820.01458.04750.31640.10010.029711.70261.24010.07510.02090.53341.99680.21060.05490.012145.80742.91010.45290.049957.07873.57861.16560.0832

表2 载荷对各阶PF分量能量矩的影响

Tab.2 The influence of motor load on energy moment of PF

载荷/kW能量矩正常滚动体故障内圈故障外圈故障PF1PF2PF3PF4PF1PF2PF3PF4PF1PF2PF3PF4PF1PF2PF3PF400.36790.14920.13420.01412.73720.23690.06030.026612.29641.63750.37180.052773.41820.81190.26610.04910.73550.38410.12710.09420.08573.24780.12780.06230.011113.19521.32330.30040.0489954.14510.63010.28470.07281.47100.34950.10640.11750.11443.33980.17310.04440.016813.31701.50780.29600.043156.81360.68820.27090.04932.20650.35310.10980.12580.07233.85400.27640.06830.018614.12092.05310.30410.038664.23751.46160.25940.0972

1) 以适当的采样频率分别对滚动轴承振动信号进行采集，收集正常工作、内圈故障、外圈故障及滚动体故障等状态下振动信号，得到相应的样本数据。

2) 采用LMD方法对样本数据进行分解，求得每个样本的PF分量。

3) 将分解所得PF分量与原始信号进行分析，将相关系数很小的分量视为虚假PF分量剔除。

5) 区分滚动轴承故障类型与损伤程度属于多分类问题，SVM解决此类问题已经提出“一对一”[11]、“一对多”[12]以及层次支持向量机等方法，综合考虑训练时间与分类效果，选用“一对一”的识别方法。将特征向量输入SVM进行训练，得到SVM分类器。

6) 将测试样本的特征向量输入训练好的SVM分类器，自动判断测试样本的工作状态与故障类别。

4 实验分析

为验证所提方法的有效性，进行滚动轴承故障分类实验。取正常运行数据10组，取载荷为0 kW，损伤程度分别为0.177 8，0.355 6及0.533 4 mm的轴承内圈故障、外圈故障及滚动体故障4种状态下测试数据各10组，形成总数为100的样本集。用字母N，I，O，B分别对应表示轴承正常、内圈故障、外圈故障及滚动体故障，字母L，M，H分别对应表示由轻到重的3种损伤程度，这样将样本集划分为10种工作状态。如果要同时区分这10种工作状态需要45个SVM分类器，为兼顾对故障类型与程度的识别效果与计算量，将所有样本组成如表3的12个测试数据集，将十分类问题简化为四分类问题，每个测试集包含40组数据，随机抽取其中30组作为训练样本，10组作为测试样本。

采用LMD分解后各PF分量的能量矩值作为特征向量对表3的测试数据集进行训练与识别，部分测试样本分类结果见表4。对于各测试数据集的分类结果如表5所示。从表中数据可以看出，以能量矩值作为特征参数在12个数据集上都表现出了较高的识别正确率，说明了PF能量矩用于滚动轴承故障诊断的有效性。同时看到，特征值对于故障类型较之故障程度表现了更高的敏感性，此方法用于故障类型的诊断效果优于故障程度。

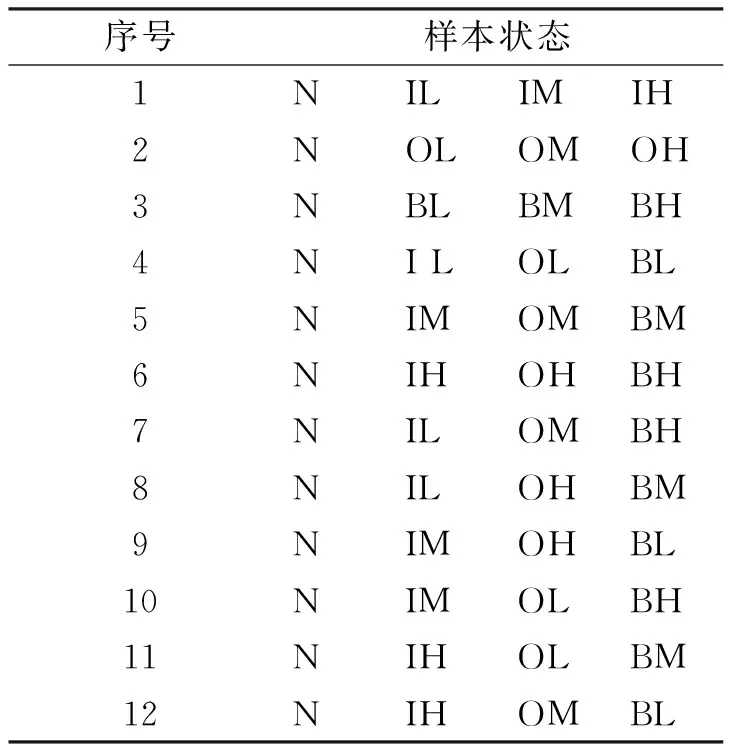
表3 测试数据集

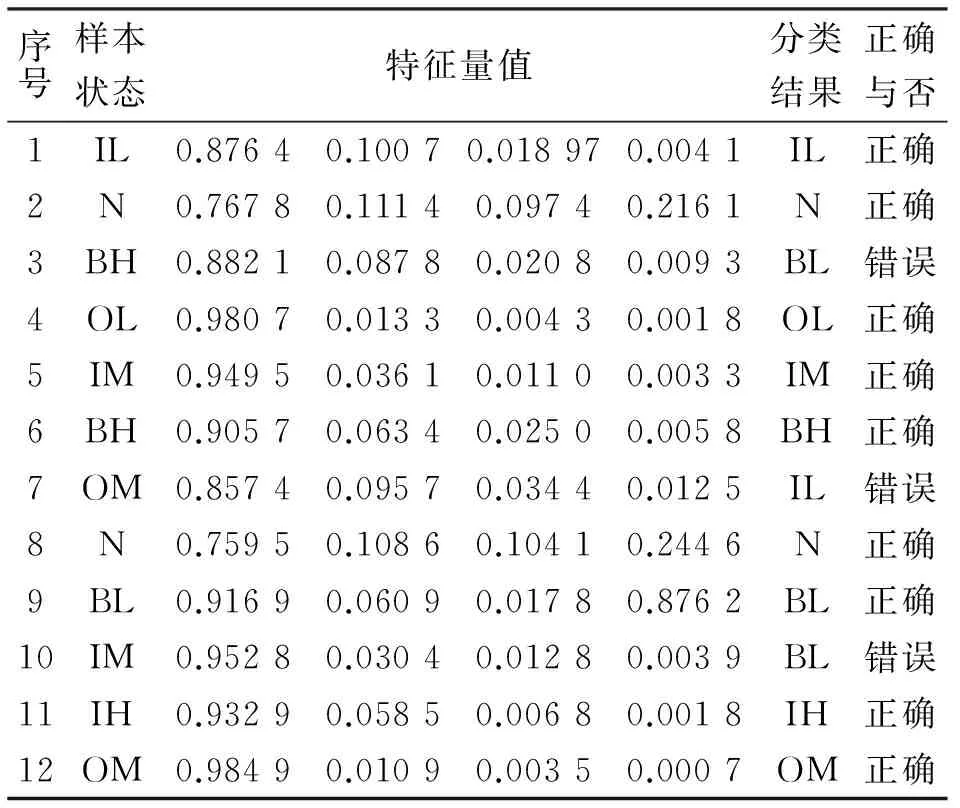
表4 部分测试样本分类结果

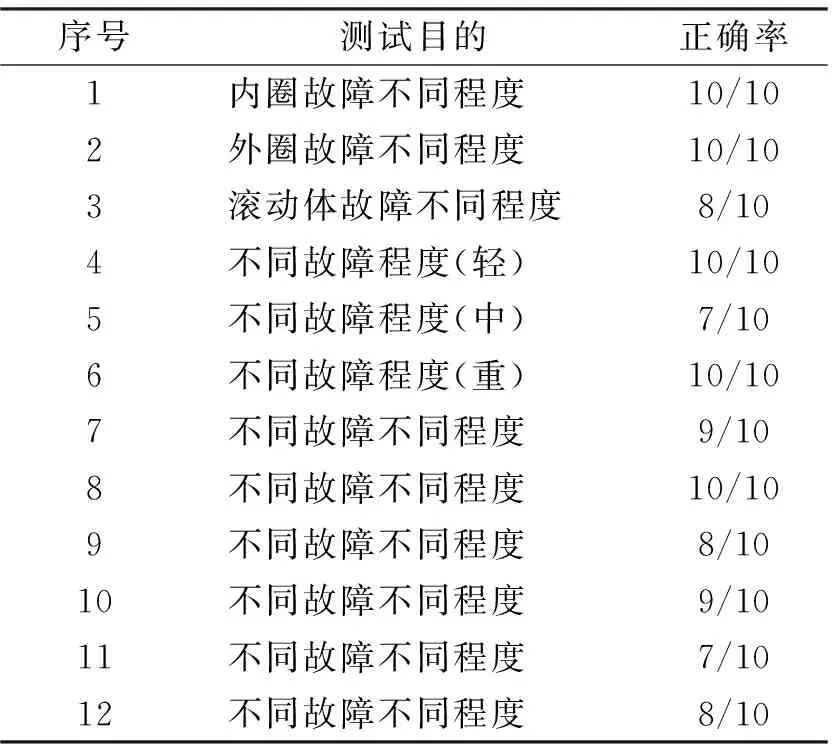
表5 轴承故障诊断分类结果

5 结 论

1) LMD作为一种自适应的信号时频分析方法，可以将复杂的调制信号分解为若干单分量且瞬时频率有意义的PF分量，每个PF分量都由包络信号与纯调频信号相乘，包含了完整的振动信号信息，通过LMD方法对滚动轴承振动信号的分析，验证了该方法处理此类信号的有效性。

2) 采用PF分量能量矩表征滚动轴承振动信号所包含的故障信息，不仅考虑了发生故障时信号能量在特定频率上的大小变化，还考虑了信号能量随时间的分布情况，相对于传统的能量算法可以更好地揭示故障发生时能量的分布特征，有利于故障特征的提取。通过对轴承正常工况、内圈故障、外圈故障以及滚动体故障振动信号的分析，表明了能量矩对于不同部件不同程度的损伤具有敏感性。

3) 提出的基于LMD能量特征与SVM故障诊断方法，对区分滚动轴承故障类型与故障程度具有较高的诊断速率与正确识别率，可有效用于滚动轴承的典型故障诊断。

[1] 孔亚林. 基于振动信号的滚动轴承故障诊断方法研究[D]. 大连：大连理工大学，2005.

[2] 张进，冯志鹏，褚福磊. 滚动轴承故障特征的时间-小波能量谱提取方法[J]. 机械工程学报，2011,47(17)：44-49.

Zhang Jin, Feng Zhipeng, Chu Fulei. Extraction of rolling bearing fault feature based on Time-wavelet energy spectrum [J]. Journal of Mechanical Engineering, 2011,47(17): 44-49. (in Chinese)

[3] 张志刚，石晓辉，施全，等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断，2013，33(3)：478-482.

Zhang Zhigang，Shi Xiaohui， Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and Spectral Kurtosis [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3):478-482. (in Chinese)

[4] 程军圣，史美丽，杨宇. 基于LMD与神经网络的滚动轴承故障诊断方法[J]. 振动与冲击，2010,29(8)：141-144.

Cheng Junsheng, Shi Meili, Yang Yu. Roller bearing fault diagnosis method based on LMD and neural network [J]. Journal of Vibration and Shock, 2010, 29(8): 141-144. (in Chinese)

[5] 刘卫兵，李志农，蒋静. 基于局域均值分解的滚动轴承故障诊断方法[J]. 轴承，2009(9)：48-52.

Liu Weibing, Li Zhinong, Jiang Jing. Fault diagnosis method of rolling bearing based on local mean decomposition [J]. Bearing, 2009(9): 48-52. (in Chinese)

[6] Smith J S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[7] 潘阳，陈安华，何宽芳，等. 基于PF能量特征和优化神经网络的轴承诊断[J]. 振动、测试与诊断，2013，33(S1)：120-124.

Pan Yang, Chen Anhua, He Kuanfang, et al. Fault diagnosis of rolling bearing based on PF energy feature and optimized artificial neural network [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(S1):120-124. (in Chinese)

[8] 张超，杨立冬，李建军. 局部均值分解和经验模态分解的性能对比研究[J]. 机械设计与研究，2012,28(3)：38-40.

Zhang Chao, Yang Lidong, Li Jianjun. The performance contrast between Local Mean Decomposition and Empirical Mode Decomposition [J].Machine Design and Research, 2012, 28(3): 38-40. (in Chinese)

[9] Radcliff G A. Condition monitoring of rolling element bearings using the enveloping technique [M]. London: Mechanical Engineering Publication Limited, 1990: 55-67.

[10]The case western reserve university bearing data center website. Bearing data center seeded fault test data[EB/OL].(2010-11-05)[2013-09-16].http:∥csegroups.case.edu/hearingdatacenter/pages/download-data-file.

[11]潘明清.基于支持向量机的机械故障模式分类研究[D]. 杭州：浙江大学，2005.

[12]刘永斌，何清波，孔凡让，等. 基于PCA和SVM的内燃机故障诊断[J]. 振动、测试与诊断, 2012,32(2)：250-255.

Liu Yongbin, He Qingbo, Kong Fanrang, et al. Fault diagnosis method of internal combustion engine based on PCA and SVM [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(2):250-255. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.004

*国家自然科学基金资助项目(51075292，51475318)；山西省科技重大专项资助项目(20111101040)

2013-02-05；

2014-02-24

TH133.33

石瑞敏，女，1983年8月生，博士生。主要研究方向为机械设备在线监测与故障诊断。曾发表《基于改进EMD的多绳摩擦提升机载荷信息特征提取》(《煤炭学报》2014年第39卷第4期)等论文。 E-mail：srm0018@link.tyut.edu.cn

杨兆建，男，1955年11月生，教授、博士生导师。主要研究方向为大型复杂机械设备状态参数监测理论与方法。 E-mail：yangzhaojian@tyut.edu.cn