体面积分方程(VSIE)分析任意复杂频率选择结构
苏建勋,李增瑞
(中国传媒大学信息工程学院,北京 100024)
1 引言
自从20世纪60年代频率选择表面(FSS)出现后,很多学者都致力研究FSS在电磁系统中的性能。近年来,超材料(Metamaterial)这类特殊的FSS也引起了人们的关注并得到了较深入的研究[1,2]。FSS在微波系统里有广泛的用途,如反射器、天线罩和极化器。随着超材料概念的出现与发展,频率选择表面作为一种平面的超材料,因具有一些神奇的特性,已被应用到一些新的方面,如平面吸收器[4,5]和人造磁导体[6]。
频率选择结构是一种平面周期结构,对电磁能量起滤波的作用。频率选择表面、电子带隙(EBG)/光子带隙(PBG)结构,超材料等,都可统称为频率选择结构。由于其越来越受到广泛的应用,故而对它的仿真技术也提出了更高的要求。有限元法(FEM)和时域有限差分法(FDTD)[7]能对周期结构进行三维(3D)建模,并且可以处理非均匀介质的情形。但计算散射场时[8]需要利用吸收边界(ABC)或完全匹配层(PML)等特殊的手段来截断无限大求解区域。
一般地,频率选择结构电磁特性满足工程指标,一是要进行贴片形状的设计,二是利用介质层复合。以往,设计工作主要集中在第一点上,而近些年来,大力开拓了介质层的复合设计。在FSS里引入周期性的非均匀介质材料,可以研究介质层复合特性的设计。例如,在介质板上钻孔[9]或者填充其他材料,改变介质基板的有效介常数或磁导率[10]。但是对于非均匀的介质层设计,无法提取分层媒质格林函数,从而很难单纯利用表面积分方程(SIE)进行建模分析。基于此,采用体面积分方程(VSIE)可以克服这些困难[11]。
本文提出了一种空域体面积分方程法用于分析频率选择结构(FSS)。其中利用Ewald变换加速周期格林函数的收敛[12,13],利用体面积分方程分析任意复杂频率选择结构,包括非均匀的介质结构或金属介质复合结构。另外,设计了一种简单有效的插值方法,能快速准确地对周期格林函数插值。
2 积分方程
2.1 体面积分方程



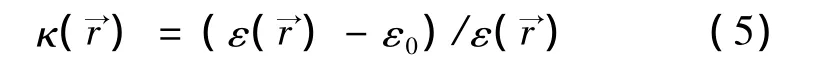
在所有的金属面S(S是闭合体或开放体),边界条件要求总电场的切向分量为零,即:
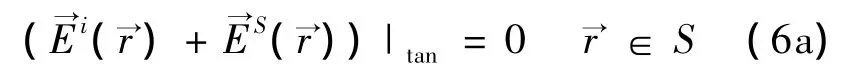
上述为电场积分方程(EFIE)。在介质区域,总电场是入射场和散射场之和。因此,体积分方程如下:
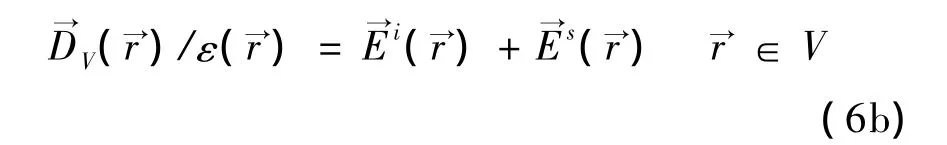
方程(6a)和(6b)结合(1)—(5),便可构建体面积分方程,其中金属面的电流为,介质区域的电通量为。混合积分方程(6)可以用伽略金矩量法精确地求解。
2.2 PGF的线性插值技术
本文的插值问题由2D变为3D,增加了一个维度,二次插值法计算效率下降。由于自由空间周期格林函数比较平滑,故而易于精确插值,因此设计了一种针对自由空间周期格林函数的精确快速插值方法。
将矩形3D框格等分为很多子格。图1是一个边长为的子格(方块)。黄点是子格顶点处预先计算后存储的PGF数值。周期格林函数可通过如下的线性插值法获得

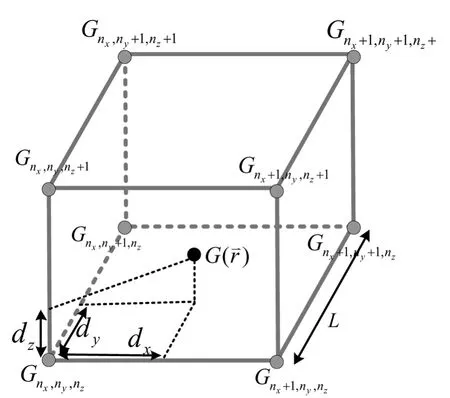
图1 子格
其中 αx=dx/L,αy=dy/L,αz=dz/L。子框格的边长范围一般为0.015-0.03λ,插值可以获得高的精度(ε >10-3)。
3 数值实例
3.1 耶路撒冷十字架
首先分析一个典型的耶路撒冷十字状的频率选择结构。像素化的单元结构如图2所示。介质板的厚度为0.02cm,相对介电常数2-j0.1。FSS的周期为a=b=2.5cm。平面波垂直入射,电场沿X方向。图3是Floquet TEM模的传输和反射系数。双Ewald序列的求和项设为9。红实线是本文方法的计算结果,黑实线是文献[15]谱域法的计算结果。由图可见,两种方法的传输和反射系数计算结果吻合良好。

图2 耶路撒冷十字FSS的单元结构图(单元尺寸是2.5cm ×2.5cm)

图3 耶路撒冷十字FSS的反射和传输系数
3.2 光子带隙结构
现在考虑一个介质材料频率选择结构,介质为非均匀的[10]。介质板嵌入周期性的介质块,如图4所示。这些栅格通常被称为光子带隙结构。图5为平面波垂直照射介质板时的反射系数。反射系数曲线展示了光子带隙材料的典型谐振特性。跟文献[13]的有限元-边界元法(FE-BI)和体积分法(VIE)的计算结果比较,本文方法计算结果的两个谐振与FE-BI吻合的良好,而VIE计算结果的两个谐振频率偏高,尤其第二个谐振频率。
3.3 基于超材料的双带通FSS
最后考虑一个基于超材料的小型化双带通FSS[16]。其中FSS为介质板两面印刷金属层的结构,介质材料为 Arlon Di- Clad 880(εr=2.2,tanδ=9E-4)。图6为该FSS的两个单元结构图。由图看出,反面金属层相对于正面金属层平移了半个周期。图7为平面波垂直入射时的仿真结果。由图7可见,本文计算结果与文献[16]中HFSS和ADS的仿真结果吻合良好。

图4 电子带隙结构

图5 TEMx模的反射系数幅度

图6 基于超材料的双带通FSS的两个周期单元

图7 双带通FSS的反射系数
4 结语
本文提出了一种空域体面积分方程(VSIE)分析具有均匀或非均匀介质层的频率选择结构。其中利用Ewald变换和插值技术快速计算空域周期格林函数。仿真结果表明,在大多数情况下,两重Ewald求和序列9项就能收敛。另外,设计了一种线性插值算法,能够快速精确地对周期格林函数进行插值,从而大大减少矩阵填充时间。数值实例结果证明了本方法的正确性和有效性。本文方法经进一步扩展,如利用体面积分方程结合自适应交叉逼近法(ACA)[17],可更加快速和精确地分析任意复杂结构的频率选择结构。
[1]T K Wu,Ed.Frequency Selective Surface and Grid Array[J].New York,Wiley,1995.
[2]B A Munk.Frequency Selective Surfaces Theory and Design[J].New York,Wiley,2000.
[3]N Engheta,R W Ziolkowski,Eds.Metamaterials Physics and Engineering Explorations Hoboken[J].NJ,Wiley,2006.
[4]N Engheta.Thin absorbing screens using metamaterial surfaces[J].Proc IEEE Antennas and Propagation Society Int Symp,San Antonio,TX,2002:392-395.
[5]G Kiani,K Ford,K Esselle,A Weily,C Panagamuwa.Oblique incidence performance of a novel fre-quency selective surface absorber[J].IEEE Trans Antennas Propag,2007,55(10):2931 -2934.
[6]D Kern,D Werner,A Monorchio,L Lanuzza,M Wilhelm.The design synthesis of multiband artificial magnetic conductors using high impedance frequency selective surfaces[J].IEEE Trans Antennas Propag,2005,53(1):8 -17.
[7]W Ko,R Mittra.Implementation of Floquet boundary condition in FDTD for FSS analysis[J].In Antennas and Propagation Society Int Symp Digest,Jun,1993:14 -17.
[8]I Bardi,R Remski,D Perry,Z Cendes.Plane wave scattering from frequency-selective surfaces by the finite - element method[J].IEEE Trans Magn,2002,38(2):641 -644.
[9]A Fallahi,M Mishrikey,C Hafner,R Vahldieck.A-nalysis of multilayer frequency selective surfaces on periodic and anisotropic substrates[J].Metamaterials,2009.
[10]H - Y D Yang,R Diaz,N G Alexopoulos.Reflection and transmission of waves from multilayer structures with planar implanted periodic material blocks[J].Opt Soc Amer,Ser B,Oct,1997,14(10):2513-2521.
[11]Lu,C C,Chew W C.A coupled surface - volume integral equation approach for the calculation of electromagnetic scattering from composite metallic and material targets[J].IEEE Trans.Antennas Propag,Dec,2000,48(12):1866 -1868.
[12]Stevanovic I,Crespo - Valero P,Blagovic K,Bongard F,Mosig J R.Integral-Equation Analysis of 3-D Metallic Objects Arranged in 2-D Lattices Using the Ewald Transformation[J].IEEE Trans Antennas Propag,Oct,2006,54(10):3688 -3697.
[13]T F Eibert,J L Volakis,D R Wilton,D R Jackson.Hybrid FE/BI modeling of 3 - D doubly periodic structures utilizing triangular prismatic elements and an MPIE formulation accelerated by the Ewald transformation[J].IEEE Trans Antennas Propag,May,1999,(5):843 -850.
[14]F W J Olver,D W Lozier,R F Boisvert,C W Clark.NIST Handbook of Mathematical Functions[M].New York:Cambridge University Press,2010.
[15]Ling Li,Werner D H,Bossard J A,Mayer T S.A model-based parameter estimation technique for wide-band interpolation of periodic moment method impedance matrices with application to genetic algorithm optimization of frequency selective surfaces[J].IEEE Trans Antennas Propag,Mar,2006,54(3):908 -924.
[16]Bayatpur F,Sarabandi K.Multipole Spatial Filters Using Metamaterial-Based Miniaturized-Element Frequency - Selective Surfaces[J].IEEE Trans Microw Theory Tech,Dec,2008,MTT -56(12):2742-2747.
[17]K Zhao,M N Vouvakis,J F Lee.The adaptive cross approximation algorithm foraccelerated method of moments computations of EMC problems[J].IEEE Trans EMC,2005,47(4):763 -773.

