基于超梁降阶模型的蒙皮加筋圆柱壳频率分析
王文胜,程耿东,郝 鹏
(1.河南科技大学 土木工程学院 工程力学系,洛阳 471023;2.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116023)
基于超梁降阶模型的蒙皮加筋圆柱壳频率分析
王文胜1,程耿东2,郝 鹏2
(1.河南科技大学 土木工程学院 工程力学系,洛阳 471023;
2.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116023)
在基于梁平截面假设的复杂结构动力模型降阶方法基础上,文章提出了建立梁超单元和超梁降阶模型的方法。通过对比考虑剪切变形的Timoshenko梁单元刚度阵,给出了梁超单元刚度矩阵的修正方法,提高了超梁降阶模型的计算精度。以蒙皮加筋圆柱壳为例,对比了超梁降阶模型与几种等效梁模型的频率分析结果。结果表明,超梁降阶模型建立方法灵活简单,具有较高的计算精度,能够为火箭结构动特性分析提供参考。
梁超单元;超梁降阶模型;剪切变形;蒙皮加筋圆柱壳;频率分析
0 引言
蒙皮加筋圆柱壳具有较高的刚度、较轻的重量等特性,被广泛应用于运载火箭等结构。由于运载火箭结构的长细比较大,因此在工程研制中,经常采用梁模型来模拟复杂的火箭结构[1-4]。针对弯曲、扭转和纵向的中低阶振动模态的火箭结构频率动特性分析,在火箭结构总体设计中具有十分重要的地位,它是载荷计算、姿态稳定性分析、POGO振动分析等工作的基础,而选取合适的计算模型则是开展相关分析的前提。
近年来,随着有限元分析软件和计算机求解能力的快速发展,已经可进行全箭结构的三维动力学建模研究工作。文献[5]采用了三维动力学模型,分析了日本H-II运载火箭的俯仰、偏航和扭转振动之间的耦合效应。采用这种模型分析的优点是便于研究速率陀螺等敏感元件安装位置的局部振型和振型斜率等问题;缺点是计算耗时,分析结果中大量的局部模态掩盖了少量设计关心的整体结构纵、横和扭转模态。而降阶梁模型具有较少的自由度,能够快速地获取结构的整体动力学响应特性,为火箭结构设计提供重要设计参数。
结构力学[6]中虽然给出了这类蒙皮加筋结构桁条面积等效和刚度等效的方法,但对桁条作用的物理原理考虑不够,没有明确给出这种等效方法的适用范围。由于实际工程中对火箭的低阶频率要求较高,直接用教科书的方法难以满足航天工程的要求。邢誉峰等[7-9]提出了基于桁条等效厚度方法的梁模型,分析了蒙皮加筋圆柱壳弯曲刚度等效方法的精度,研究了等效方法中的扭转刚度计算问题,并指出等效厚度梁模型可直接用于计算弯曲和纵向固有振动频率。该方法对于火箭整体结构的相关分析具有实际应用和参考价值,但扭转频率的计算结果偏高,需要进行修正,本文称这种梁模型为等效厚度梁模型。栾宇[10]给出了根据结构静力响应计算这类结构等效刚度及截面参数的梁模型降阶方法,本文称为静力等效梁模型。本文在基于梁平截面假设的动力模型降阶方法[11-12]的基础上,提出了建立梁超单元的方法,且通过与Timoshenko梁单元刚度矩阵对比,对梁超单元刚度阵引入了考虑剪切变形的修正,得到了计算精度较高的超梁降阶模型。通过典型蒙皮加筋圆柱壳算例,与等效厚度梁模型及静力等效梁模型进行了对比,数值结果表明了超梁降阶模型的有效性。
1 超梁降阶模型的建立
针对细长梁式结构,文献[11-12]中提出了基于梁平截面假设的动力模型降阶方法,此处稍作叙述。经典的Euler梁弯曲理论以及考虑剪切变形的Timoshenko梁弯曲理论中,都假定变形前垂直于中心线的截面变形后仍保持为平面[13]。如图1所示,根据细长梁式结构的特点,在发生非局部变形时,截面的变形可近似为刚体位移,可采用平截面假定来描写。根据这一假定,任意一个截面i上任一点j和截面形心处的6个基本准刚体模态之间可建立如下位移映射关系:
uj=Rjqi
(1)
其展开形式为
(2)
式中uj表示第j点的位移向量;qi表示截面i形心处的准刚体模态;Rj表示j点的位移转换矩阵;xcj,ycj,zcj表示第j点坐标与截面i形心坐标的差值。
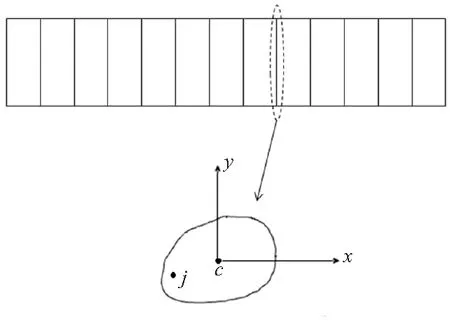
图1 模型降阶示意图
对于结构上第i个截面,截面内的m个节点均凝聚到该截面形心处,则有:
Ui=Tiqi
(3)
式中Ui=(ui1,…,uim)T表示这一截面内m个节点的位移向量;Ti=(Ri1,…,Rim)T表示这一截面的位移转换矩阵。
在此基础上,本文取任意2个相邻截面(截面i和截面i+1)之间的结构部分为一梁段,梁段上所有节点的位移U可表示为
(4)
假设梁段的刚度阵和质量阵分别为k、m,利用式(4)可得到:
kR=TTkT,mR=TTmT
(5)
式(4)中,Q是12×1的列向量,因此式(5)中凝聚得到kR、mR均为12×12的矩阵,分别表示凝聚后的梁超单元的刚度阵和质量阵。式(4)中的T表示建立梁超单元的降阶基向量。kR、mR可按照序列组装成一个超梁降阶模型的总刚度阵和总质量阵,如果模型均匀,只需要建立一次梁超单元;反之,则需要建立若干个梁超单元。
2 超梁降阶模型的修正
Timoshenko梁单元引入了横向剪切变形来修改梁单元刚度阵中的弯曲刚度项,具体推导过程可在文献[14-16]中查到。考虑一根主轴与坐标x重合,梁截面关于x-y平面对称的空间均匀梁,其Timoshenko梁单元刚度矩阵可表示为
(6)
(7)
(8)
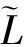
如果Iy=Iz,则φy=φz,可统一表示成φ。
由式(7)可得
(9)
又因为
(10)
将式(9)及式(10)代入到式(8)中,φ值可求得:

(11)

kT=kb1+kb2+kb3+kat
(12)
式中kb1只包含(Y1,Y2,Z1,Z2)项;kb2只包含(Y3,Z3)项;kb3只包含(Y4,Z4)项;kat只包含与轴向和扭转刚度有关的(X,S)项。
上述通过降阶得到的梁超单元刚度阵中,本文认为其弯曲刚度项与Timoshenko梁单元具有相同的物理意义,同样可分解为与式(12)类似的4部分:
kR=kRb1+kRb2+kRb3+kRat
(13)

(14)
将整个结构沿长度方向剖分为p个这样的梁段,则修正过弯曲刚度项后的超梁降阶模型的总刚度阵可表示为
(15)
以ANSYS软件为例,在建立实际壳体结构的复杂有限元模型后,本文采用APDL(ANSYSParametricDesignLanguage)二次开发语言实现梁段刚度矩阵k、质量矩阵m的数据输出。在ANSYS的输出数据中没有模型降阶减缩基T矩阵,本文同时利用APDL语言程序实现了T矩阵的建立和输出。利用式(5)得到梁超单元的刚度阵kR和质量阵mR,并将kR分解为4个部分,提取刚度阵中的(X,S)值计算剪切修正系数进行修正;然后,组装超梁降阶模型的总刚度阵和质量阵,调用特征值分析程序实现原结构的快速频率分析。
3 等效厚度梁模型和静力等效梁模型概述
为了对比方便,本节简述一下等效厚度梁模型及静力等效梁模型。文献[7-9]中给出了基于桁条等效厚度方法建立的等效梁模型,在蒙皮和桁条材料弹性常数接近时,等效光筒圆柱结构的平均厚度为
(16)

在此基础上,对于蒙皮加筋结构的等效梁模型,其拉伸、弯曲和扭转刚度由材料弹性常数和横截面面积、惯性矩、极惯性矩确定。其中横截面面积、惯性矩、极惯性矩按式(17)计算。
(17)
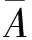
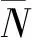
(18)
利用式(16)~式(18)计算得到这些结构参数后,可很方便地在有限元软件中建立相应的等效梁模型,用来模拟原蒙皮加筋结构。本文利用ANSYS软件实现这一过程。
4 数值算例
本章通过2个具体算例的频率分析,以比较本文提出的超梁降阶模型与其它模型。
4.1 均匀蒙皮加筋圆柱壳算例
算例1为图2所示自由-自由的均匀ISOGIRD网格蒙皮加筋圆柱壳。模型长9 976 mm,外径2 000 mm,蒙皮厚度为10 mm,网格筋条高30 mm,筋条厚25 mm。采用铝合金,弹性模量70 GPa,泊松比0.3,密度2.7×10-3g/mm3。采用ANSYS壳单元(SHELL181)建立有限元模型,3 472个节点,20 832个自由度。
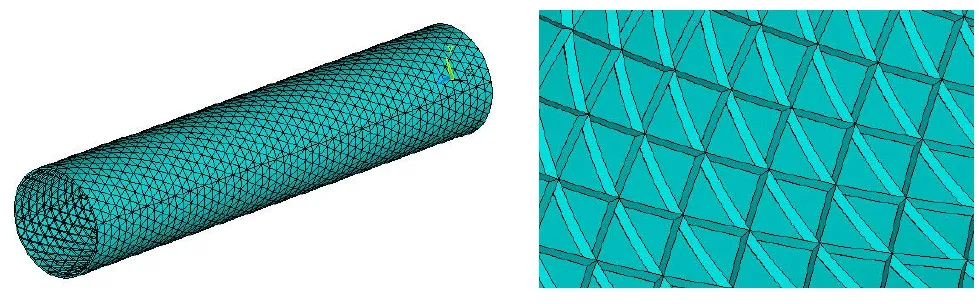
图2 均匀网格蒙皮加筋圆柱壳有限元模型及局部放大图
利用式(16)可求出光筒壳等效厚度为16.2 mm,并根据式(17)计算其横截面面积、惯性矩、极惯性矩。

δN=0.014 877 mm,θp=0.158×10-3rad
φT=0.38×10-7rad
进而可按照式(18)计算静力等效梁模型参数如下:
分别按照上面得到的数据,利用BEAM188梁单元,建立与超梁降阶模型自由度数相等的等效梁模型,用于模拟原结构的动力学分析。
基于超梁降阶模型方法,将原结构模型沿轴向划分为55个梁段。由于模型是均匀结构,因此只需要建立一个梁超单元,便可按照次序组装成具有55个梁超单元,336个自由度的超梁降阶模型。对于这类结构,k取值为2.0[17],提取梁超单元刚度阵中的(X、S)值,并计算得到φ=0.340 8,则按照式(14)计算并取近似值β=0.73,进而可按照式(15)修正超梁降阶模型。
在此基础上,分别利用上述3种降阶梁模型模拟了原结构模型在自由-自由、一端固支及两端固支边界条件下的特征值分析,计算结果分别如表1~表3所示。

表1 自由-自由状态下几种降阶梁模型频率计算结果对比

表2 一端固支状态下几种降阶梁模型频率计算结果对比

表3 两端固支状态下几种降阶梁模型频率计算结果对比
从表1~表3中的频率计算结果可知,静力等效梁模型计算精度最高,但建立一次降阶梁模型至少需要3次原结构静力分析,如果原结构参数改变(如长度变化),则需要重新求解式(18)中的参数。等效厚度梁模型计算精度较差,尤其是扭转频率的计算结果,说明等效厚度梁模型不能直接用于计算扭转频率,文献[8]中给出了具体的修正方法,此处不再叙述。
超梁降阶模型的各阶频率计算结果与相应阶次ANSYS软件的计算结果很接近。当对实际工程结构低阶动力特性分析精度要求不很高时,为设计人员提供了一个有效简单的计算模型,且建立模型工作量很小,只要利用已经建立的原结构有限元模型的数据建立一个梁超单元,便可组装成不同长度的超梁降阶模型,剪切修正系数的计算过程也较为简单。需要指出的是超梁降阶模型一端固支一端自由及两端固支频率结果,是在自由-自由状态的降阶模型上施加相应的边界约束条件计算得到。
为了进一步修改和使用降阶梁模型,工程师们更希望获得降阶梁模型的截面参数,即得到降阶梁模型的轴向刚度、抗弯刚度、抗扭刚度和质量分布等。表4分别给出了利用3种梁模型计算得到的图1所示的ISOGIRD网格蒙皮加筋圆柱壳的轴向刚度EA及截面抗弯刚度EI。

表4 3种梁模型的轴向及抗弯刚度

利用原结构截面几何形状计算截面参数时,不同截面的轴向刚度和抗弯刚度均不同。因此,这里没有把它们简单列入表中。对于本算例,按截取位置不同(轴向加筋处和环向加筋处),分别计算得到相应的轴向刚度EA及截面抗弯刚度EI为:轴向加筋处,轴向刚度7.104 2×109N,截面抗弯刚度34.630×1014N·mm2;环向加筋处相应值为17.052×109N及82.828×1014N·mm2。从这些结果中可看到,等效厚度梁模型截面参数与原结构轴向加筋处的截面参数基本一致,这是因为建立等效厚度梁模型时,只考虑了沿轴向筋条的等效。超梁降阶模型的截面参数介于原结构轴向加筋与环向加筋两处的截面之间,这是因为超梁降阶模型考虑了环向加肋的影响,更真实地反映了原结构的截面性质。此外,由于本文在超梁降阶模型上考虑了剪切变形修正,能更好地用于近似实际结构。
4.2 非均匀蒙皮加筋圆柱壳算例
算例2为图3所示沿长度方向加筋非均匀的自由-自由圆柱壳结构,模型由蒙皮、轴向及环向桁条组成。模型长20 m,蒙皮厚度0.01 m,桁条沿径向高度均为0.1 m。将结构分为3部分:第一部分长度10 m,直径1 m,轴向桁条厚度为0.05 m,环向桁条厚度为0.03 m;第二部分长度2 m,轴向桁条厚度为0.04 m,环向桁条厚度为0.05 m;第三部分长8 m,直径0.8 m,轴向桁条厚度为0.03 m,环向桁条厚度为0.04 m。所用材料与算例1一致。模型共有2 064个节点,2 520个单元,12 384个自由度。

图3 非均匀网格加筋圆柱壳模型及局部放大图
根据结构形式的不同,在结构第一、三部分分别建立1种梁超单元,第二部分建立6种梁超单元;然后,将超单元进行组装,将原结构模型降阶为具有42个梁超单元,258个自由度的超梁降阶模型。分别提取各种梁超单元刚度阵中的(X、S)值,并计算其修正系数,本文取这些系数的平均值β=0.95作为该超梁降阶模型的修正系数。同时,利用式(16)~式(18),分别计算等效厚度及静力等效梁模型的参数,利用ANSYS软件建立与超梁降阶模型自由度数相等的等效梁模型。表5给出了自由-自由边界条件下算例2采用3种梁模型的频率计算结果。
表5所示计算结果表明,对于非均匀蒙皮加筋结构,超梁降阶模型也能用于原结构的快速近似动力分析,且计算精度也高。在此基础上,在自由-自由状态的降阶模型上施加相应的边界约束条件,即可计算相应约束条件下原结构的频率,只需非常小的额外工作量。

表5 非均匀网格加筋圆柱壳降阶梁模型频率计算结果对比
5 结论
(1)在基于梁平截面假设的结构动力模型降阶方法的基础上,给出了建立梁超单元和超梁降阶模型的方法。
(2)通过对比Timoshenko梁单元刚度矩阵,考虑了剪切变形,给出梁超单元刚度矩阵的修正方法,建立了计算精度较高的超梁降阶模型。
(3)典型蒙皮加筋圆柱壳模型算例的频率分析结果表明,超梁降阶模型具有较高计算精度,且可处理不同情况和约束条件下的结构模型,对火箭结构频率动特性分析具有实际应用和参考价值。
[1] Zipfel P H. Modeling and simulation of aerospace vehicle dynamics[M]. 2nded.. American Institute of Aeronautics and Astronautics, Inc., Virginia., USA, 2007.
[2] 王龙生,张德文. 火箭结构有限元分析的若干问题[J]. 强度与环境, 1988(3): 45-53.
[3] 王毅,朱礼文,王明宇,等. 大型运载火箭动力学关键技术及其进展综述[J]. 导弹与航天运载技术, 2000, 243(1): 29-37.
[4] 邱吉宝,王建民. 运载火箭模态试验仿真技术研究新进展[J]. 宇航学报, 2007, 28(3): 515-521.
[5] Yoshiki Morino. Vibration test of 1/5 H-II launch vehicle[R]. AIAA 87-D783.
[6] 龚尧南. 结构力学 [M]. 北京: 北京航空航天大学出版社, 2001.
[7] 潘忠文,王旭,邢誉峰,等. 基于梁模型的火箭纵横扭一体化建模技术[J]. 宇航学报, 2010, 31(5): 1310-1316.
[8] 潘忠文, 邢誉峰, 杨阳. 蒙皮加筋圆柱壳扭转频率的三种计算模型[J]. 北京航空航天大学学报, 2011, 37(9): 1156-1159.
[9] 邢誉峰,潘忠文,杨阳. 蒙皮加筋圆柱壳弯曲频率的三种计算模型[J]. 北京航空航天大学学报, 2012, 38(4): 1-6.
[10] 栾宇. 航天器结构中螺栓法兰连接的动力学建模方法研究 [D]. 大连: 大连理工大学, 2011.
[11] 王文胜,程耿东,李取浩. 基于梁平截面假设的复杂细长结构动力模型降阶方法[J]. 计算力学学报, 2012, 29(3): 295-332.
[12] Wang Wen-sheng, Cheng Geng-dong, Li Qu-hao. Fast dynamic performance optimization of complicated beam type structure based on two new reduced physical models[J]. Engineering Optimization, 2013, 45(7):835-850.
[13] Timoshenko S P, Gere J M. Mechanics of materials[M]. 1sted.. Van Nostrand Reinhold Company, New York, 1972.
[14] Cowper G R. The shear coefficient in Timoshenko's beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.
[15] Narayanaswami R, Adelman H M. Inclusion of transverse shear deformation in finite element displacement formulations[J]. AIAA Journal, 1974, 12:1613-1614.
[16] Severn R T. Inclusion of shear deflection in the stiffness matrix for a beam[J]. The Journal of Strain Analysis for Engineering Design, 1970, 5(4):239-241.
[17] Robert D C, David S M, Michael E P. Concepts and applications of Finite Element Analysis[M]. 4thed.. John Wiley & Sons Inc, New York, 2001.
(编辑:薛永利)
Frequency analysis of stiffened cylindrical shell based on reduced super beam model
WANG Wen-sheng1, CHENG Geng-dong2, HAO Peng2
(1.Department of Engineering Mechanics, School of Civil Engineering,Henan University of Science and Technology, Luoyang 471023, China;2.Department of Engineering Mechanics, State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology, Dalian 116023, China)
A type of super beam element and reduced super beam model were presented by means of the model reduction method, which is based on the plane cross-section assumption of beam. The stiffness matrix of the super beam element was modified by considering the effect of shear deformation in an elegant way, resulting in a reduced super beam model with high accuracy. Typical stiffened cylindrical shell model, served as the illustrative example for frequency analysis, were employed to compare the reduced super beam model with several other equivalent beam models. The results show that the reduced super beam model is easy to construct with high accuracy, which can provide references for the dynamic analysis of rocket structures.
super beam element;reduced super beam model;shear deformation;stiffened cylindrical shell;frequency analysis
2014-07-03;
2014-08-11。
国家自然科学基金(11402077,11402049);河南科技大学科学研究基金(13350046);中国博士后科学基金(2014M551070)。
王文胜(1983—),讲师,研究方向为复杂结构动力模型降阶及结构优化设计。E-mail:wswang@live.cn
V414
A
1006-2793(2015)03-0401-06
10.7673/j.issn.1006-2793.2015.03.020

