基于新型滑模控制方法的再入飞行器姿态控制律设计
李宪强,周 军,郭建国
(西北工业大学 精确制导与控制研究所,西安 710072)
基于新型滑模控制方法的再入飞行器姿态控制律设计
设计了一种新型滑模控制方法,该方法不但能对已有的控制律进行鲁棒性改进,而且能有效抑制抖振现象。在该方法的设计过程中,首先基于已有的控制律和标称系统,设计了一种新型的动态滑模面,然后对超扭曲算法进行改进,得出了一种快速、连续且有限时间收敛的算法,并首次将其作为新型趋近律,该趋近律与滑模面相结合能够大大增强现有控制律的鲁棒性,而且滑模的切换律是连续的,因此大大降低了系统的抖振。将以上方法应用于再入飞行器的姿态跟踪控制中,有效增强了已有控制律的鲁棒性,实现了大干扰情况下对姿态系统的稳定控制。通过仿真,验证了该方法在提高系统鲁棒性和降低抖振方面的有效性。
滑模控制;超扭曲;再入飞行器;动态滑模面;抖振抑制
0 引言
滑模控制具有快速全局收敛特性、易于实现性、模型降阶、对外部干扰的鲁棒性,以及对系统参数和建模误差的不敏感性[1-2],因而被广泛用于航空航天领域[3-5]。
目前,关于滑模控制方法的研究取得了很多成果。很多学者设计了各种滑模控制方法,除了常规的基于线性滑模面[6-7]的控制以外,还有各种基于非线性滑模面的控制方法,如终端滑模控制[8]、非奇异终端滑模控制[9]、快速非奇异终端滑模控制[10]等。其中,根据文献[11]中提出的滑模相对阶的概念可知,以上文献中的方法都是一阶滑模控制方法。为此,有学者设计了高阶滑模控制方法,如超扭曲滑模算法[12],并基于此发展出了变参数超扭曲算法[13]及自适应参数超扭曲算法[14]等。 以上文献中,滑模控制方法分别具有不同的优良特性,如有限时间收敛和减少抖振等特性等,但它们不具有对标称系统已有的控制方法进行鲁棒性改进的功能。在实际工业控制过程中,对现有的控制器进行鲁棒性改进,相比推翻现有的控制器再重新设计来说,能大大节省经济成本和时间成本。对此,本文基于标称系统和现有控制方法,设计了一种新型的动态滑模面,在滑模面上系统等价于标称系统。因此,只要滑模面收敛到零点,就能有效利用已有的控制器,使系统稳定。
滑模控制在实际应用中,存在着抖振现象,抖振现象主要是由于控制指令中含有不连续的切换控制律,从而导致执行机构的跟踪速率过快。在滑模面到达零点时,执行机构由于惯性作用,其速率难以衰减到零点,使得系统不断穿越滑模面,从而形成抖振现象。抖振的表现形式就是滑模面在零附近不断振荡,抖振降低了系统的鲁棒性和稳定精度,甚至可能激发未建模动态,破坏系统的稳定性[15]。目前,在这方面也已经取得了很多成果。主要有边界层法[16]、干扰估计方法[17]、高阶滑模方法[12-14,18]以及最近出现的类低通滤波器方法[19]。其中,边界层法只能保证滑模面稳定在零附近,因此削弱了系统的鲁棒性,并容易引起稳态误差;高阶滑模控制方法降低颤振的思想是将不连续的切换项隐藏在切换律的导数中;干扰估计是通过利用观测器对系统的干扰进行补偿,以降低切换指令的幅值,并实现降低抖振。类低通滤波器方法是首先将一个不连续的切换项经过一个类似于低通滤波器系统后的信号等效成系统的实际控制输入,然后设计切换控制项,由于切换控制项将会经过类低通滤波器的滤波,无论切换控制项是否连续,系统的实际输入都是连续的,因此降低了抖振。本文不同于以上方法,从趋近律的角度入手,通过设计连续且有限时间收敛的高阶趋近律,同样达到了良好的抖振抑制效果。
文中设计的滑模面和趋近律相结合,可对已有的控制方法进行鲁棒性改进,而且得出的指令是连续的,从而抑制了抖振,将文中设计的方法应用在再入飞行器的姿态控制中,成功地对已有的鲁棒性不好的控制器进行了改进,最终实现了对整个系统的稳定控制。应用过程中,首先基于时标分离假设,将系统分成快、慢回路子系统,其次采用文中的滑模控制方法,分别针对快慢子回路已有的控制器进行了鲁棒性改进。
1 问题描述
针对如下形式的系统:
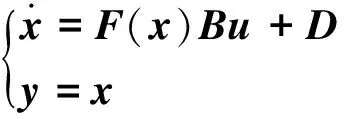
(1)
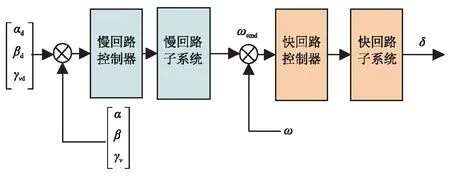
其中,x∈Rn×1为状态,y为输出,F(x)∈Rn×1为与状态相关的项,B∈Rn×n为可逆的输入分配矩阵,u∈Rn×1为输入,D∈Rn×1为匹配性干扰,能够表示D=B·δ,且‖δ‖ 假设系统存在着一个鲁棒性不太好的控制律uequ,仅能够在系统(1)中干扰D=0,或者干扰较小时,使系统稳定。接下来要研究的问题是如何采用滑模控制方法对现有的控制律uequ进行鲁棒性改进,使系统在更大的干扰下,仍能够保持稳定,且设计的滑模控制律能有效抑制抖振现象的发生。 假设系统(1)的标称系统(D=0时的系统),已经存在一种稳定的控制律uequ,由于uequ是针对标称系统设计的,因此uequ的鲁棒性不强。 令对uequ进行鲁棒性改进后的控制律具有如下形式: u=udis+uequ (2) 式中uequ为标称控制律;udis为待设计的修正律。 针对式(1)设计如下滑模面: (3) 如果能够合理设计趋近律,并求出udis,控制s稳定到零点,则此时系统等价于如下稳定的系统: (4) 接下来设计一种新型的趋近律,保证s有限时间内收敛到零点,且有效减小抖振的发生。 对超扭曲算法(SA)进行改进,设计一种快速超扭曲算法(FSA),并将其作为新型趋近律。 引理1:(SA)考虑如下系统[12] υ (5) (6) 引理2:存在如下系统[20] (7) 引理1给出的SA在远离零点时收敛较慢,但在接近零点时收敛速度较快,且是有限时间收敛的,引理2给出的控制系统是指数收敛的。因此,其在远离零点时的收敛速度较快,接近零点时的收敛速度较慢。接下来,结合二者优点设计一种FSA。 定理1:(FSA)存在如下系统 (8) 证明系统(8)等价于如下系统: (9) 取李雅普诺夫函数如下: (10) 取ξ=[|e|1/2sign(e1)e1e2]T,则对式(10)求导,可得 (11) 其中 ω1=[-k1ρ1-k2ρ10]T 根据|ρ1|≤p1+p2|e1|,可得 (12) 其中 根据式(11),可得 (13) 接下来,证明系统是有限时间稳定的。 式(10)又可写成如下形式: V=ξTQξ (14) 其中 所以,V满足: (15) 根据式(15),可得 (16) (17) 根据ξ=[|e1|1/2sign(e1)e1e2]T,可得 ‖ξ‖2≥|e1|1/2 (18) 结合式(17)和式(18),可得 (19) 将式(16)和式(19)代入式(13),可得 (20) 其中 (21) 根据有限时间收敛控制理论可知,根据式(20)即可判定V是有全局限时间收敛的。 式(8)形式的系统既能保证在远离零点时的收敛速度,还能保证有限时间收敛。在存在干扰的情况下,式(8)是连续且有限时间收敛的,如果将其作为趋近律,则能够保证滑模面有限时间收敛到原点,而且能够抑制抖振。 在本章中,将利用前文的新型滑模面和新型趋近律,最终确定出滑模控制律。 假设模型(1)中的干扰D的元素满足‖D(i)‖≤p1i+p2i‖s(i)‖,且s(i)表示s的第i(i=1,2,…,n)个元素。 针对式(3)所示的滑模面,采用如定理1中式(8)形式的趋近律,即 (22) 其中 k1=diag(k11k12k13),k2=diag(k21…k2n) k3=diag(k31…k3n),k4=diag(k41…k4n) 将式(3)进行求导,并代入式(22),可得 (23) 将式(2)代入式(23),可得滑模切换控制律为 udis=B-1× (2) 所以,将式(24)代入式(2)中,可得出经过鲁棒性修正的控制律为 (25) 定理2:假设系统(1)的标称系统(D=0时的系统),已经存在一种稳定的控制律uequ,但由于uequ是针对标称系统设计的,因此uequ的鲁棒性不强。此时,对控制律进行改进,采用式(25)形式的控制律,则系统(1)在存在大干扰情况下,即使仅采用uequ已不能使其保持稳定,但经改进后的控制律式(25),则能有效控制系统(1)稳定。 证明:将控制律式(25)代入系统式(1)中,得 (26) (27) (28) 由于uequ是标称系统的稳定控制律,因此在存在大干扰D时,采用经过改进的控制律式(25),能够确保系统(1)是稳定的。 (29) 经过比对可发现,t>T1后,式(25)的udis=-B-1D。因此,可知干扰D能够在有限时间内被udis完全抵消掉,从而保证了uequ的控制性能不再受到任何干扰的影响。从这点也说明了式(25)比控制律uequ具有更强的抗干扰能力。综上可知,定理2成立。 根据控制律式(25)可知,其不含有不连续的切换项。因此,能够有效降低抖振。 当系统(1)中的干扰为零时,此时系统为标称系统,如果选取滑模面的初值为零,则式(25)中修正项udis始终为零。因此,在系统不含干扰时,文中的鲁棒性改造方法不会降低uequ对标称系统的控制效果。 高超声速再入飞行器的姿态运动学和动力学跟踪模型如下[21-22]: (30) 其中,eη=η-ηd为姿态角跟踪误差;η=[αβγv]T为姿态角,其元素分别表示攻角、侧滑角和滚转角;ηd=[αdβdγvd]T为期望的姿态角;ω=[pqr]T的元素分别表示滚转角速率、俯仰角速率和偏航角速率;Dx=[dx1dx2dx3]T和Dy=[dy1dy2dy3]T表示不确定性,主要包括外部干扰和未建模动态,u=[δxδyδz],其中各项的具体表达形式可参见文献[21]。 基于时标分离假设[22-23],系统(30)可分解成慢回路子系统和快回路子系统。慢回路子系统的跟踪误差动态特性为 (31) 首先设计慢回路的控制器ωcmd,然后将其作为快回路的指令输入,令eω=ω-ωcmd。因此,可得快回路的动态方程为 (32) 最后,设计快回路控制器u,确保系统(30)稳定。 以上控制思想如图1所示。 图1 快慢回路控制结构框图 假设已经针对慢回路式(31)的标称形式(Dx=0),设计了如下控制器: (33) 其中,ls=diag(ls1,ls2,ls3),lsi>0(i=1,2,3)。 假设已经针对快回路式(32)的标称形式(Dy=0),设计了如下控制器: (34) 其中,eω=ω-ωequ,lf=diag(lf1,lf2,lf3),lfi>0(i=1,2,3)。 由于快、慢回路子系统动态方程具有与式(1)相同的形式,因此可根据定理2,分别对原快慢回路控制器式(33)和式(34)进行鲁棒性改进。具体过程不再赘述,给出改进后的控制器如下: 鲁棒性改进后的慢回路控制器: (35) 鲁棒性改进后的快回路控制器: (36) 仿真过程中,飞行器的气动参数来自于文献[23],大气数据来自于文献[24]。在慢回路中存在干扰:Dx=[0.20 0.15 0.10]Tsin(5t)rad。姿态角初值为α=5°,β=0.5°,γv=55°;期望的姿态角为αd=6°,βd=0°,γv=54°。为了作为对比,将原快慢回路的FL控制律(式(33)和式(34)),与采用文中滑模方法对(33)和式(34)改进后的快慢回路控制律FLSMC(式(35)和(36))以及与式(37)形式的传统滑模控制方法(CSMC)[25]同时进行仿真。 (37) 其中,滑模面为 (38) 选FL的参数为ls=diag(10.5 10.5 10.5),lf=diag(36.2 36.2 36.2)。 选FLSMC参数为ls=diag(10.5 10.5 10.5),lf=diag(36.2 36.2 36.2),ksi=diag(1.5 1.5 1.5),kfi=diag(1.0 1.0 1.0),i=1,2,3,4。 TSMC的参数选取如下:Cs=diag(0.1 0.1 0.1),ks=diag(0.1 0.1 0.1),εs=diag(0.22 0.20 0.12),Cf=diag(0.1 0.1 0.1),kf=diag(0.2 0.2 0.2),εf=diag(0.03 0.02 0.02),λ=500。 仿真过程中发现,在已有的FL控制律的作用下,系统直接发散。其他仿真结果见图2~图4。根据图2可知,文中FLSMC控制律能够对系统稳定控制。因此,可说明经鲁棒性改进后的FLSMC控制律比FL控制律具有更强的鲁棒性。此外,通过图2还可知,FLSMC控制律相比常规的滑模控制CSMC具有更高的控制精度,造成这一结果的原因可由图4间接说明。图4中,显示了将慢回路修正律udis乘以-b1后与干扰实际值的比较结果。根据结果可知,修正律udis能够对干扰进行精确补偿,保证了本文控制方法能够通过精确补偿干扰,大大提高系统的鲁棒性。此外,由于常规滑模控制方法不能对干扰进行精确补偿,因此保证了本文方法相比常规滑模控制方法具有更高的控制精度。根据图3可知,文中设计的方法输入量相比常规滑模控制方法的输入量更加平滑,文中设计的方法可减少系统抖振的发生。造成这种结果的主要原因是文中采用了连续的趋近律,使得控制律不含容易引起系统抖振的符号项。因此,有效降低了抖振效应。 图2 姿态跟踪误差收敛效果图 图3 输入对比结果图 综上所述,新型滑模控制方法能够有效增强已有控制方法的鲁棒性,且该滑模控制方法产生的控制指令是连续的,使得该控制指令相比常规滑模控制指令更平滑,从而大大降低了抖振效应。 图4 慢回路中FSASMC滑模切换控制律对干扰的补偿效果 文中设计了一种对现有控制律进行鲁棒性增强的滑模控制方法,该方法具有以下特点: (1)该方法能够有效增强现有控制律的鲁棒性; (2)在模型不含干扰情况下,该方法不会降低现有控制律的控制性能; (3)该方法能够抵消干扰对于控制系统带来的影响; (4)该方法是连续的,因此有效降低了抖振的发生; (5)该方法的通用性较强。 [1] Sabanovic A.Variable structure systems with sliding modes in motion control-a survey[J].IEEE Transactions on Industrial Informatics,2011,7(2):212-223. [2] Feng Yong,Han Feng ling,Yu Xing huo.Chattering free full-order sliding-mode control[J].Automatica,2014,50 (4):1310-1314. [3] Alwi H,Edwards C.Fault detection and fault-tolerant control of a civil aircraft using a sliding-mode-based scheme[J].IEEE Transactions on Control Systems Technology,2008,16(3):499-510. [4] Gaspar P,Szaszi I,Bokor J.Reconfigurable control structure to prevent the rollover of heavy vehicles[J].Control Engineering Practice,2005,13(6):699-711. [5] Corradini M L,Orlando G.Linear unstable plants with saturating actuators:robust stabilization by a time varying sliding surface[J].Automatica,2007,43(1):88-94. [6] Hall C,Shtessel Y.Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1315-1328. [7] Chang J L,Chen Y P.Sliding vector design based on the pole-assignment method[J].Asian Journal of Control,2000,2(1):10-15. [8] Man Z,Yu X.Terminal sliding mode control of MIMO linear systems[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,1997,44(11):1065-1070. [9] Feng Yong,Yu Xing-huo,Man Zhi-hong.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167. [10] Yang Liang,Yang Jian-ying.Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879. [11] Arie levant.Sliding order and sliding accuracy in sliding mode control[J].International Journal of Control,1993,58(6):1247-1263. [12] Arie levant.Robust exact differentiation via sliding mode technique [J].Automatica,1998,34(3):379-384. [13] Tenoch Gonzalez,Moreno,Leonid Fridman.Variable gain super-twisting sliding mode control[J].IEEE Transactions on Automatic Control,2012,57(8):2100-2105. [14] Shtessel Y,Taleb M,Plestan F.A novel adaptive-gain supertwisting sliding mode controller:methodology and application[J]. Automatica,2012,48(5):759-769. [15] Boiko I,Fridman L.Analysis of chattering in continuous sliding-mode controllers[J].IEEE Transaction on Automatic Control,2005,50(6):1442-1446. [16] Utkin V.Sliding modes in control and optimization[M]. Berlin,Germany:Springer-Verlag,1992. [17] Shtessel Y B,Shkolnikov I A, Brown M D J.An asymptotic second order smooth sliding mode control[J].Asian Journal of Control,2003,5(4):498-504. [18] Bartolini G,Ferrara A,Usai E.Chattering avoidance by second-order sliding mode control[J].IEEE Transactions on Automatic Control,1998,43(2):241-246. [19] Vadim I Utkin,Alex S Poznyak.Adaptive sliding mode control with application to super-twist algorithm:Equivalent control method[J].Automatica,2013,49(1):39-47. [20] 孙长银,穆朝絮,张瑞民.高超声速飞行器终端滑模控制技术[M].北京:科学出版社,2014:117-128. [21] Elmar M Wallner,Klaus H Well.Attitude control of a reentry vehicle with internal dynamics[J].Journal of Guidance,Control,and Dynamics,2003,26(6):846-854. [22] Du Yan-li,Wu Qing-xian,Jiang Chang-sheng,et al.Adaptive functional link network control of near-space vehicles with dynamical uncertainties[J].Journal of Systems Engineering and Electronics,2010,21(5):868-876. [23] Costa R R da,Chu Q P, Mulder J A.Reentry flight controller design using nonlinear dynamic inversion[J].Journal of Spacecraft and Rockets,2003,40(1):64-71. [24] Voegt S,Burkhardt J,Muller S,et al.Credits-model and algorithm description[R]. Astrium Space Infrastructure,TET-DASA-18-SW-2185,Bremen,Germany,1999. [25] Tigges M A.Preliminary V-201 entry flight pro.le with landing site precision,cycle-8[R].NASA V-201-NOI 175,Oct.1998. (编辑:崔贤彬) Design of a novel sliding mode controller for the attitude control of reentry vehicle LI Xian-qiang,ZHOU Jun,GUO Jian-guo (Institute of Precision Guidance and Control,Northwestern Polytechnical University,Xi’an 710072,China) A novel sliding mode control method was proposed in this paper,which is not only capable of improving the robustness of the existing control law,but can also effectively attenuate chattering.In the design process,a novel dynamic sliding mode surface was designed firstly based on the nominal system and the existing control law.Then the super-twisted algorithm was improved.A fast continuous and finite time convergence algorithm was obtained,which was adopted as the novel reaching law for the first time.The reaching law combined with the sliding mode surface can greatly enhance the robustness of the existing control law.In addition,since the sliding mode switching law is continuous,the chattering was greatly attenuated. The proposed method was then applied to attitude tracking control of reentry vehicle and the robustness of the existing control law was effectively enhanced under large disturbance.Finally,the effectiveness of the method was demonstrated through simulation. siding mode control;super-twisting algorithm;reentry vehicle;dynamic sliding surface;chattering attenuate 2014-11-12; 2014-12-14。 国家自然基金(61304238);国家863计划(2012AA120602)。 李宪强(1986—),男,博士生,研究方向为导航、制导与控制。E-mail:1740679934@qq.com 李宪强,周 军,郭建国 (西北工业大学 精确制导与控制研究所,西安 710072) TJ765.3 A 1006-2793(2015)03-0301-07 10.7673/j.issn.1006-2793.2015.03.0012 新型滑模面设计
3 新型滑模趋近律设计
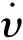
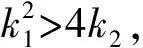
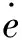
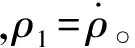
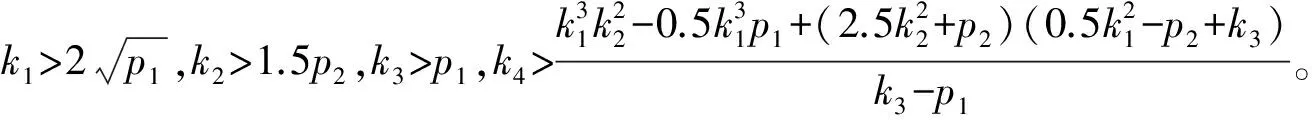
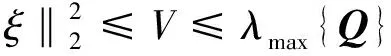
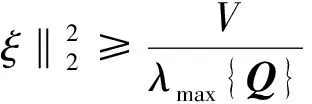
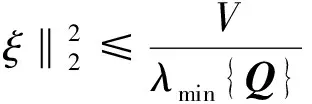
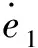
4 滑模控制律的求取
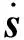
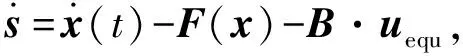
5 新型滑模控制方法在再入飞行器姿态控制中的应用
6 仿真分析
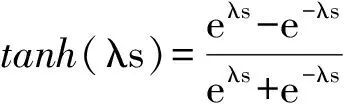
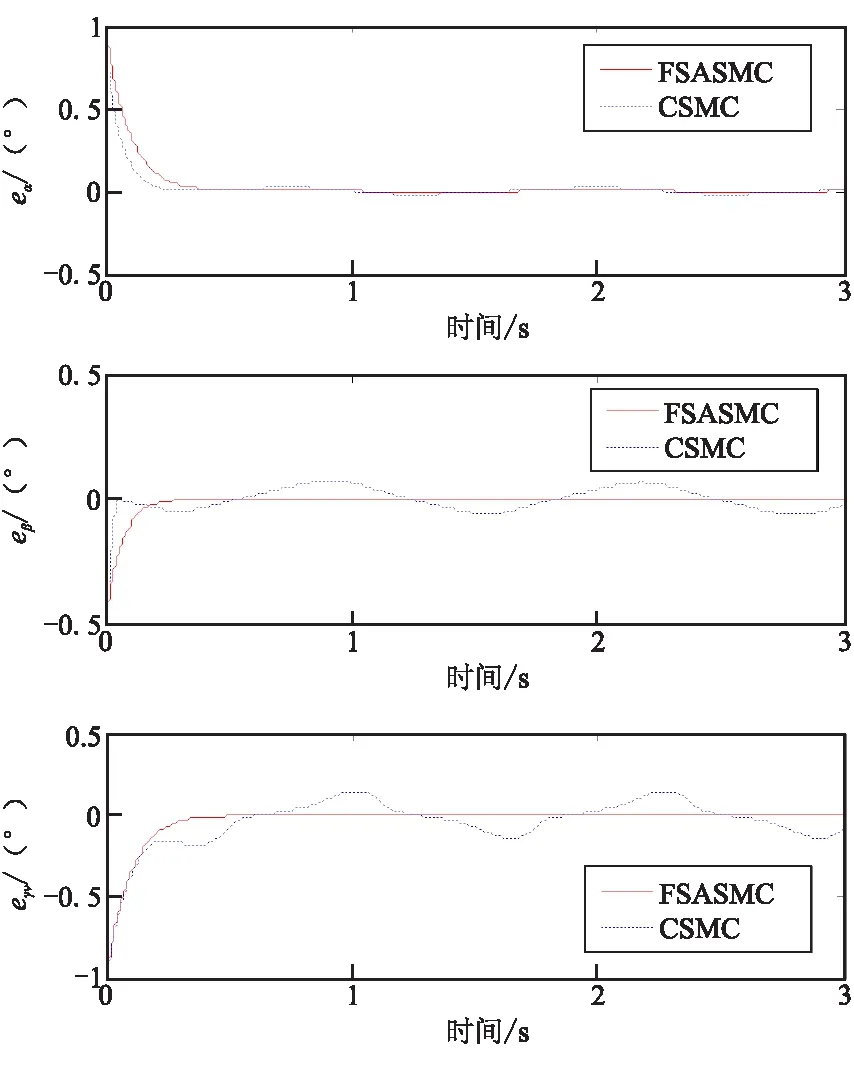
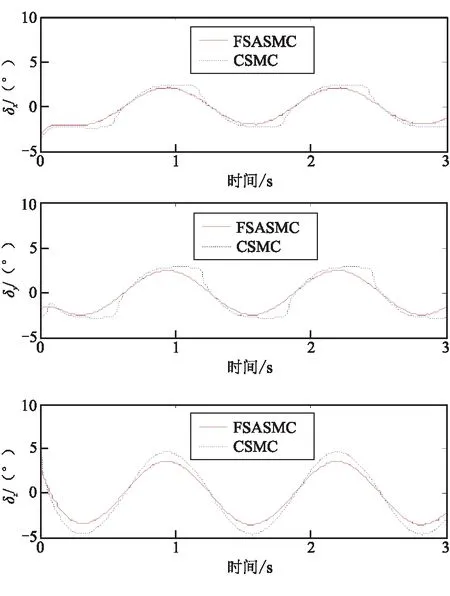
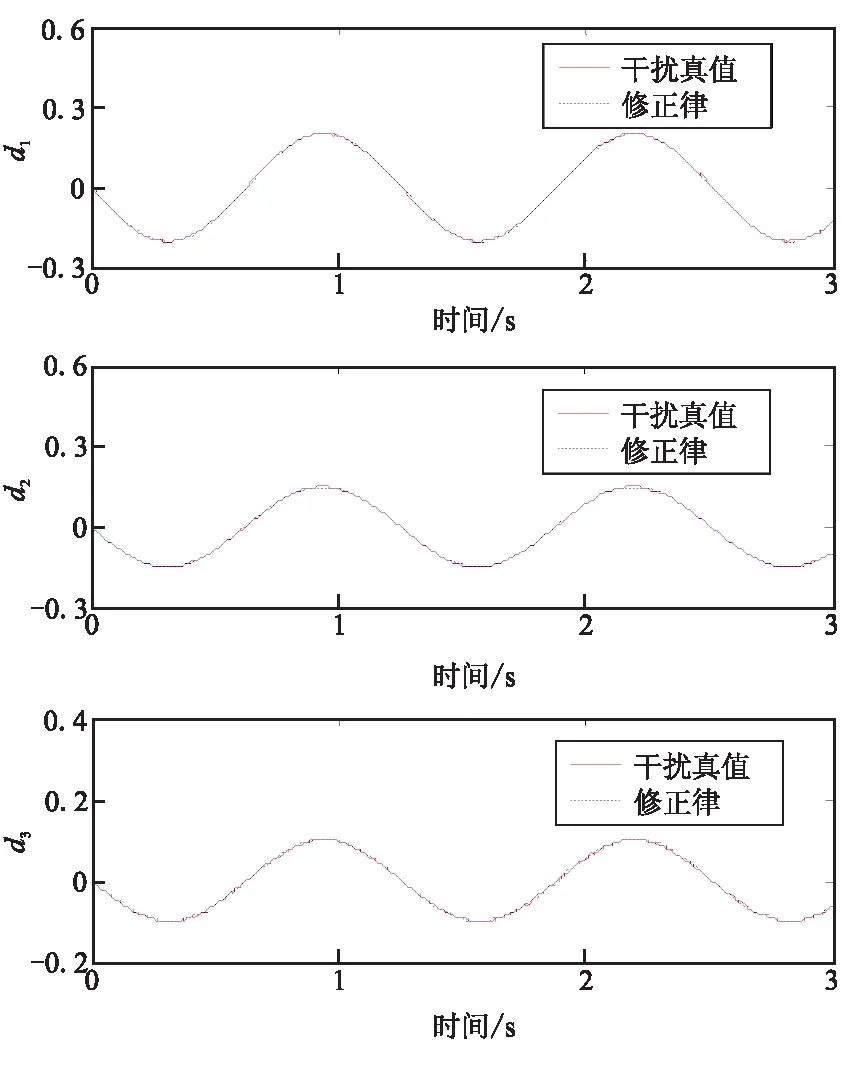
7 结论

