基于连锁故障模型的电网风险评估研究
陈 睿,杨银国,钱 峰,王延纬,冯 雷,朱 林(.广东电网有限责任公司电力调度控制中心,广东广州 50600;.华南理工大学电力学院,广东广州 5064)
基于连锁故障模型的电网风险评估研究
陈睿1,杨银国1,钱峰1,王延纬1,冯雷2,朱林2
(1.广东电网有限责任公司电力调度控制中心,广东广州510600;2.华南理工大学电力学院,广东广州510641)
摘要:提出了一种基于连锁故障模型的电网风险评估新方法。较传统基于N-1、N-2故障扫描的风险评估方法,该方法全面计及了线路的过载切除、安全稳定装置和线路保护隐性故障等影响连锁故障发展的因素,重点考虑了线路保护的多重隐性故障这类复杂情况,通过引入贝叶斯网络确定可能发生的各故障序列概率,最后定义了线路风险、节点风险这两项核心指标,从而实现了对电网风险程度的量化与评价。以IEEE30节点系统为例的仿真表明了本算法的有效性。
关键词:连锁故障;风险评估;风险指标
0 引言
电力系统运行部门通常采用诸如全网N-1和部分区域N-2的典型故障情况评估电网存在的风险。随着电网的控制水平和冗余性不断提升,个别元件的故障已难以威胁到系统的安全。纵观近几年的国内外事故,可发现严重事故很大程度上是由元件的相继失效的连锁故障所引起[1]。传统的基于N-k的风险评价方式只是评估了源发故障阶段的风险情况,但缺少深入挖掘源发故障发生后可能继续失效的连锁路径及其可能的最大负荷损失。因此,把连锁故障纳入到电网风险评估范畴,对提高电网的安全运行水平有重要的意义。
国内外学者在连锁故障领域已开展了许多研究工作。有学者立足于电力系统分析的角度提出了OPA模型、CASCADE模型、分支过程模型等[2-7]。这些模型的特点是以潮流计算为基础,因而能够较好地刻画潮流的转移过程,但控制策略的选择依赖潮流的计算结果。因此,这类模型与故障的实际演化过程存在一定差异。
也有学者基于复杂网络理论进而提出了小世界模型、相隔中心性模型、有效性能模型等等[8-13]。这些模型从图论的视角研究了连锁故障的过程。尽管这类模型计算速度快,但模型推导的假设条件过于理想,难以吻合电力系统的实际运行情况,因而会存在结果可信度问题。
另外,在连锁故障影响因素的分析方面也取得了较大的突破。在连锁故障中线路保护隐性故障是扩大故障范围的重要因素,许多学者研究了考虑线路保护隐性故障因素的连锁故障模型[14-17]。但必须提及的是,在上述的研究工作中只考虑线路保护的单一隐性故障。
本文在连锁故障模型中全面考虑了过载线路的切除、线路保护隐性故障和安全稳定装置等影响故障演化过程的关键因素,并且还进一步地充分考虑线路保护的多重隐性故障所带来的复杂可能情况。将上述因素全部计及后,故障序列多而复杂,相应的各故障序列的概率计算成为了风险评估的难点。贝叶斯网络可表达复杂变量关系而结构简单[18],本文采用贝叶斯网络确定各故障序列的概率。在定义了线路风险指标和节点风险指标后,可实现对电网风险的量化评价。本文所提方法能较好满足电力系统运行部门对电网风险梳理和掌控的工作需求。
1 考虑多因素的连锁故障模型
1.1连锁故障的发展过程
电力系统的实际运行经验表明,连锁故障为电力系统的安全运行带来挑战。连锁故障开始于某一个或某几个元件失效的源发故障(N-k),进而发生一系列的相继事件,最终形成N-k-x1-x2…-xn。这些事件在时间上具有先后性,在因果上具有较强关联性,是一个伴随着低压、过载、频率波动等系统响应以致保护频繁动作的复杂过程[19]。
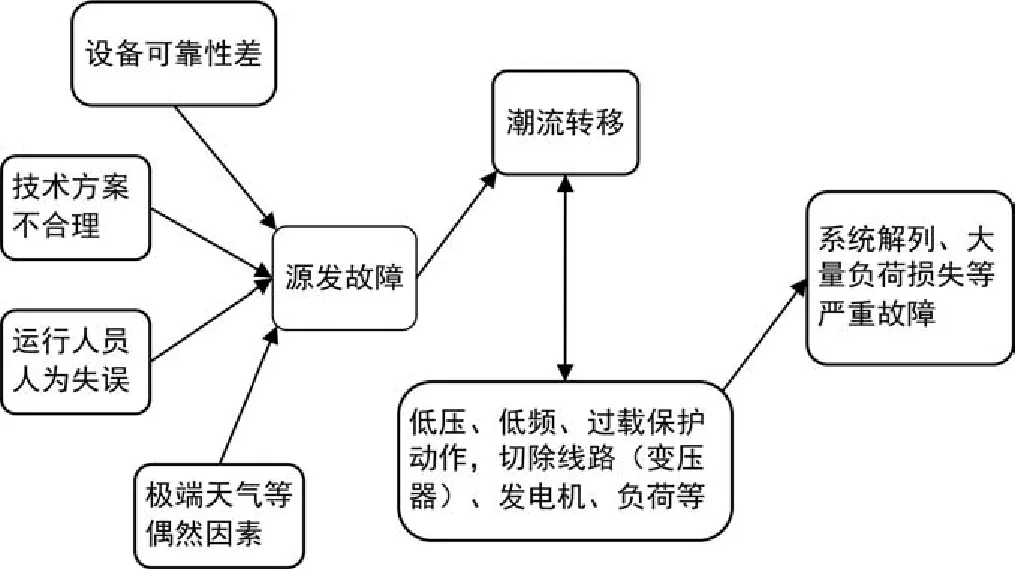
图1 连锁故障发生示意图
图1显示了连锁故障的发展过程。当负荷较重,电网运行在比较接近极限的状态时,由于设备因素、技术因素、管理因素和天气等偶然因素,电网发生了源发故障。故障将导致电网的网络拓扑发生改变,随后的潮流转移等过程使保护或自动装置动作,再次发生潮流转移等过程,如此反复循环,最终导致系统解列或大量负荷损失等严重后果。
1.2影响连锁故障各因素的作用分析
本文全面考虑了影响连锁故障发展的多类因素,如下。
(1)线路过载切除
出现故障后,系统潮流发生变化。一旦线路(本文所指线路包括输电线路和变压器)所流过的有功功率大于线路的热稳定极限时,保护必须动作以切除该线路。
(2)安全稳定装置
依据电力系统安全稳定装置的实际动作逻辑,对安全稳定装置的动作情况进行模拟,包括低压减载,过流减载等。例如对一个采用了分k级切除的分散型低压减载装置的负荷节点,当负荷节点电压低于设定值Vset-1时,切除m1%负荷;当节点电压继续降到低于Vset-2时,切除m2%负荷,以此类推,当节点电压最后降到低于设定值Vset-k时,切除mk%负荷。
(3)线路保护隐性故障
电力系统故障过程中,在完成一个开关动作后,线路保护装置可能由于定值不当以及硬件损
坏等原因而误动[15]。本文选用了图2所示的模型描述线路保护的隐性故障[20]。P表示保护动作的概率,PH为保护因隐性故障而动作的概率,F表示线路通过的有功功率,FH为线路额定有功功率,Flim为线路热稳定有功极限。

图2 线路保护隐性故障特性
从诱发连锁故障的因素分析来讲,隐性故障的作用不容忽视。以线路保护为例,其隐性故障在正常方式下不会发生,一般暴露于某线路断开后与之相连的所有线路[21]。如图3所示,当线路L4发生故障被切除时,线路L1、L3、L5、L6的保护都有可能发生隐性故障,而L2的保护认为不处于隐性故障的发生区域。本文对线路保护的多重隐性故障进行考虑,即线路L4被切除后,线路L1、L3、L5、L6的保护有可能同时发生误动。
1.3连锁故障模型的建立
由于交流潮流在电网发生高阶故障后收敛性较差,且交流潮流不收敛时,难以合理地估计故障后果,本文采用直流潮流算法。另外,当电网发生故障后,调度人员往往是根据其经验进行调度,若采用最优潮流模拟调度行为,跟实际情况还是有差距。而且,风险评估应该是反映由故障带来的风险,不应包含调度员决策的影响。因此,本文不对调度行为进行模拟,这同时也可减少计算量。

图3 隐性故障示意图
当满足以下任一条件后,连锁故障的模拟终止:(1)某次线路跳开后,没有出现隐性故障,没有出现线路过载,安全稳定装置未动作;(2)系统形成孤岛,但不包括单个节点的失去。
结合影响连锁故障各类因素的作用,得出连锁故障的计算流程如图4所示。

图4 连锁故障模型计算流程
2 基于贝叶斯网络的故障概率计算
连锁故障的复杂性,使其故障序列存在多种的可能分支,计算各分支情况的概率是风险评估中的难点。贝叶斯网络是通过有向无环图表示一组随机变量和随机变量间条件概率分布的图形模型,适于进行涉及因果或推理关系的概率计算,且相比于事件树等其他模型,贝叶斯网络结构简单且规模随问题增加呈线性增长[18]。连锁故障是始于源发故障的一系列相继事件,每一阶段的故障都与上一阶段的故障有紧密关系,非常适合运用贝叶斯网络进行分析。
可通过分析连锁故障过程中第k阶段与第k+1阶段演化过程的关系,确定贝叶斯网络的节点与结构,如图5所示。

图5 连锁故障的贝叶斯网络模型
第k阶段结束时,对任一在第k阶段中断开的线路Li,建立“线路Li断开”节点,其条件概率pi可通过第k-1阶段与第k阶段的贝叶斯网络模型计算出(k=1时则为源发故障发生概率)。线路Li断开将可能触发相邻线路隐性故障的发生,第k+1阶段开始。由于存在多重隐性故障的情况,即各线路都有隐性故障的可能,故对与线路Li相连的所有线路Li1、Li2、Li3…Lin,建立“线路Lim隐性故障”节点(1≤m≤n),各节点的条件概率可分别由保护的隐性故障模型得出。确定各个线路隐性故障的情况后,切除过载的线路,得到一种系统状态,建立“系统状态”节点,显然系统取各状态的条件概率即为“线路Lim隐性故障”节点(1≤m≤n)取相应值时的联合概率分配。此时第k+1阶段结束。
同时为提高运算速度,做如下简化处理:1)在一个阶段内发生多重的隐性故障时,当该情况概率小于预设的极小正数ε时,可近似将该情况的概率取为0;2)当在一个阶段中,已经有线路保护发生了隐性故障,则后面的阶段中线路保护发生隐性故障的概率近似为0。
3 风险指标计算
3.1线路风险指标
根据风险理论[22],风险事件A的风险值为风险事件A的概率与风险事件A造成的后果严重度的乘积。因此,可以定义线路风险指标,即:

式(1)中,Fi为第i个线路源发故障,Riskb(Fi)为第i个源发故障的风险值,P(Fi)为第i个源发故障的发生概率,Sev(Fi)为第i个源发故障的后果严重度。
风险评估在电网企业中的实际应用需求是着重考察源发故障对系统带来的后果危害性,因此本文将源发故障的概率取为1。以解析的方法对源发故障后的多种故障序列进行综合考虑,本文将源发故障带来的后果严重度定义为源发故障发生后,负荷损失的期望值,即
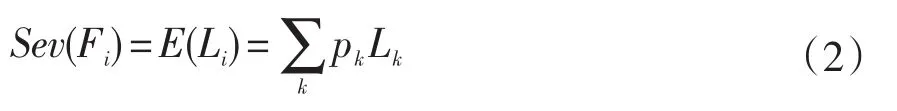
式(2)中,pk和Lk分别为源发故障后第k种故障序列的概率与相应的负荷损失。
该指标直接反映了源发故障发生后系统损失的负荷,与当前电网企业采用的事故评价方法(如国务院599号令等)可以较好地衔接,可根据需要进一步修改作为事故评级的依据。
3.2节点风险指标
本文参考复杂网络理论中节点的度的概念[23],并以线路风险指标作为边的权重,定义节点风险指标:

式(3)中,Ni为第i个节点,S为与节点Ni相邻的线路集合,Fm为第m个线路源发故障。显然,与节点相连的线路数量越多,或者线路风险指标越大,则节点风险指标越大。节点风险指标与当节点失去而与之相连的线路均断开时所造成的系统损失负荷成正相关,可直观地评价节点在系统中的重要性。
3.3风险指标的计算步骤
基于连锁故障模型的电网风险评估步骤如下:1)形成预想故障集。令k=1。
2)确定第k个源发故障。令m=1。
3)确定第k个源发故障发生后,第m种故障序列中发生保护隐性故障的线路。开断故障线路,按图4所示流程进行连锁故障分析,得出负荷损失,并按第2节的方法计算该故障序列的概率。
4)若m达到上限值,转到步骤5,否则m= m+1,回到步骤3。
5)计算第k个源发故障的风险指标。若k达到上限值,风险评估结束,否则k=k+1,回到步骤2。
计算过程中,可储存中间文件记录故障序列信息,掌握电网可能存在的连锁故障路径。
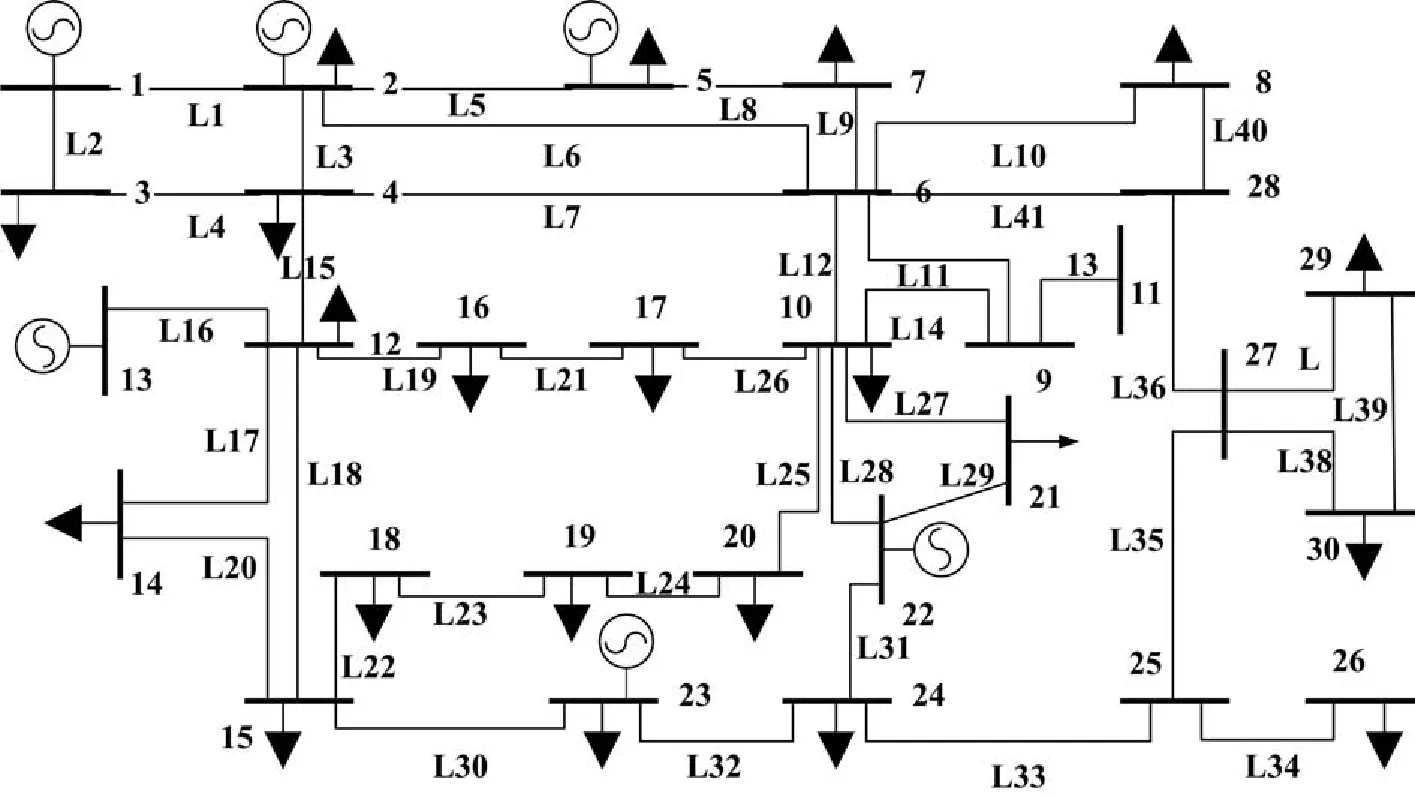
图6 IEEE 30节点系统
4 算例分析
本文以文献[24]中的IEEE 30节点系统为例,评估电网的运行风险,对算法的有效性进行验证。初始参数设置如下:PH为0.02,Pact为1。
表1列出了风险值较大的前35个源发故障。以源发故障L41为例,说明连锁故障的发生过程。L41由于故障断开后,与之相连的L6,L7,L9,L10,L11,L12,L36,L40均有发生隐性故障的可能。若是L10和L40发生隐性故障,将损失负荷30 MW;若是L10,L11和L12发生隐性故障,L21,L32,L33,L35将过载跳开,最后将导致负荷损失46.5 MW。
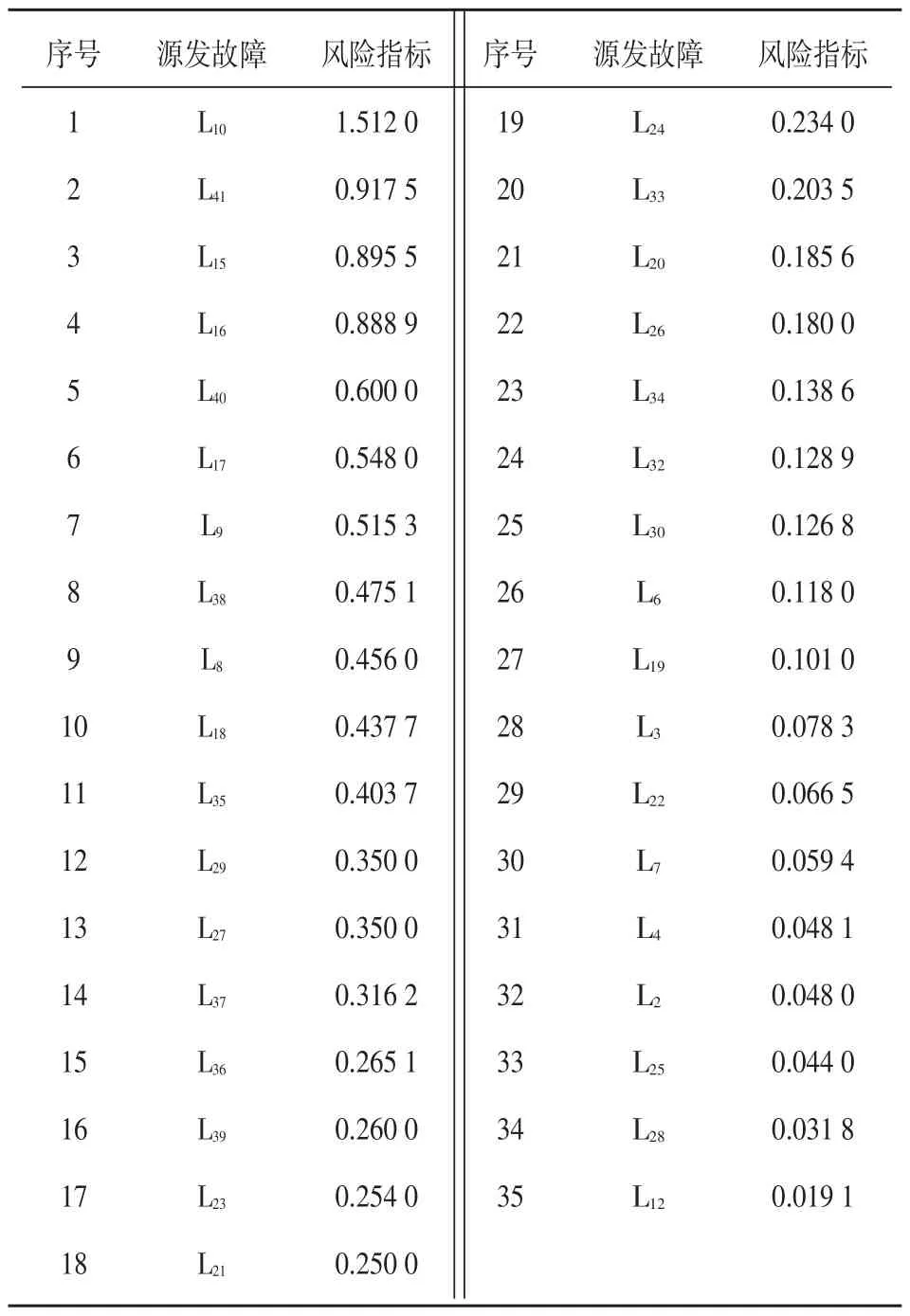
表1 线路源发故障风险指标
从表1可以看出,L10,L40和L41具有较大的源发故障风险,而L10和L40是向节点8送电唯一的两个通道,L10故障,L40保护误动或者L40故障,L10误动都可轻易地使节点8的负荷丢失。而L41与L10和L40均相连,L41故障,L10或L40误动也易引发连锁故障使得节点8负荷丢失。另外,L15,L16和L17也具有较高的风险,原因是若L15,L16和L17发生隐性故障相继退出运行,则节点14的供电必须依靠L20,此时将使L30过载并引发一列连锁故障造成较大的负荷损失。由此可见,该评估方法得出的结果与对系统进行分析的结果是一致的。
表2列出了各节点的风险指标。从表2可看出,节点6具有最高的风险,原因是与节点6相连的线路数量较多,有7条,而且其中4条线路的风险指标排在表1的前7位。通过节点风险指标可以很直观地看出节点在系统中的重要性。
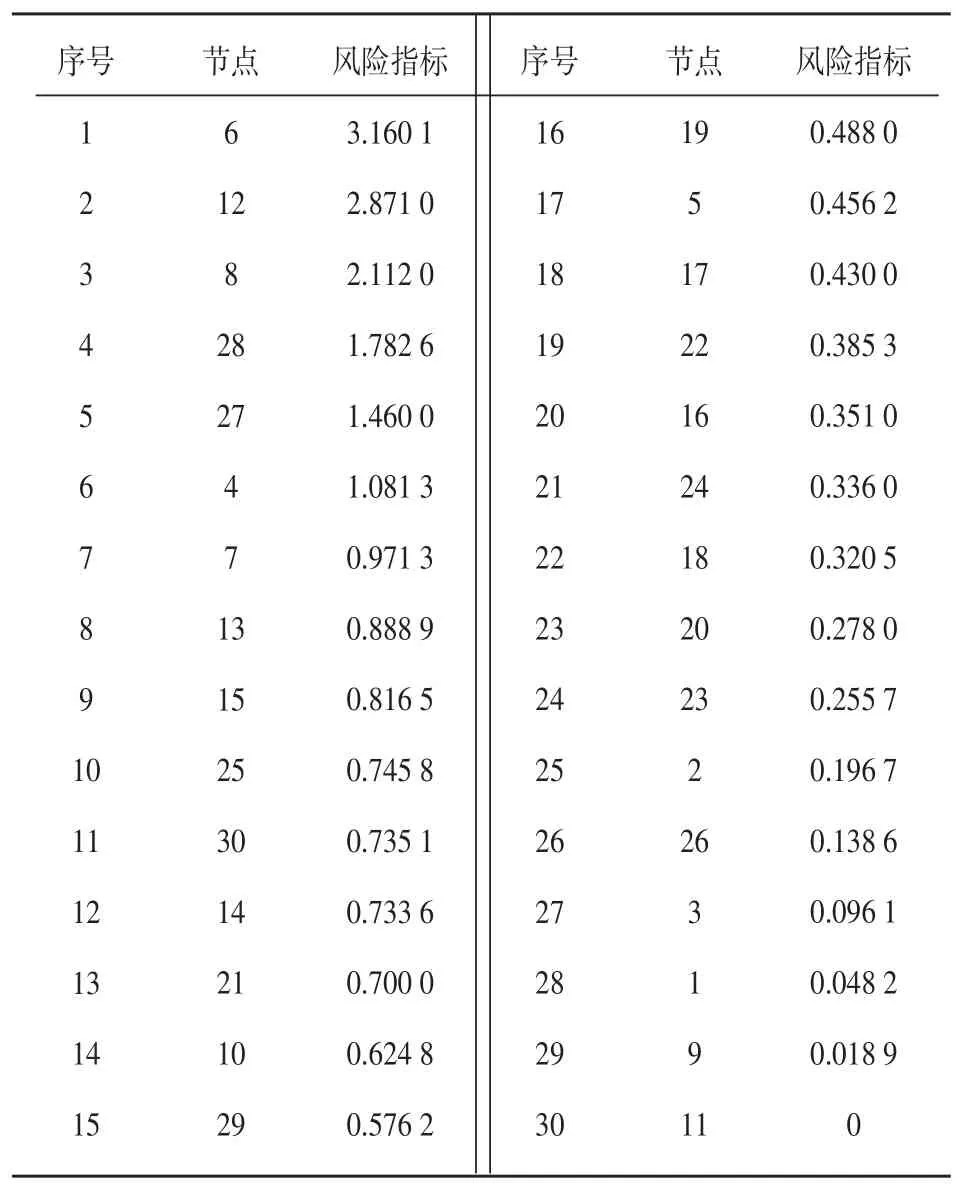
表2 节点风险指标
从以上分析可以看出,连锁故障可对系统造成灾难性的损失,在对运行方式进行校核或者电网运行风险进行评估时,应该考虑连锁故障的作用。
5 结论
连锁故障是导致电网发生严重事故的重要故障形式,对电网运行风险进行评估时,应该考虑连锁故障的作用。本文提出了考虑了连锁故障的运行风险评估方法。评估过程中充分考虑了多重保护隐性故障的复杂情况。定义了线路风险指标和节点风险指标,评估结果可为运行人员找出当前运行方式下的重要线路和关键节点,并发现可能存在的连锁故障路径,以便做好风险预防控制措施。
参考文献:
[1]孙可,韩祯祥,曹一家.复杂电网连锁故障模型评述[J].电网技术,2005,29(13):1-9.
[2]Dobson I,Chen J,Carreras B A et al. Examining criti⁃cality of blackouts in power system models with cascading events[A]. Hawaii InternationalConference on System Science,Hawaii,2001.
[3]梅生伟,何飞,张雪敏,等.一种改进的OPA模型及大停电风险评估[J].电力系统自动化,2008,32(13):1-5.
[4]Dobson I,Carreras B A,Newman D E. A probabilistic loading-dependent model of cascading failure and possi⁃ble implications for blackouts[A]. Hawaii International Conference on System Science,Hawaii,2003.
[5]Dobson I,Carreras B A,Lynch V E et al.Complex sys⁃tems analysis of series of blackouts:cascading failure,criticality,and self-organization[A]. Bulk Power Sys⁃tem Dynamics and Control-VI,Italy,2004.
[6]Dobson I,Carreras B A,Newman D E. A branching pro⁃cess approximation to cascading load-dependent system failure[A]. 35thHawaii International Conference on System Science,Hawaii,2004.
[7]Dobson I,Carreras B A,Newman D E. A criticality ap⁃proach to monitoring cascading failure risk and failure propagation in transmission systems[A]. Electricity Transmission in Deregulated Markets Conference,Pitts⁃burgh,2004.
[8]Watts D J,Strogatz S H.Collective dynamics of ‘small-world’networks[J]. Nature,1998,393(6):440-442.
[9]Surdutovich G,Cortez C,Vitilina R et al.Dynamics of “small world”networks and vulnerability of the electric power grid[A]. VIII Symposium of Specialists in Elec⁃tric Operational and Expansion Planning,2002.
[10]Holme P,Kim B J. Vertex overload breakdown in evolving networks[J]. Physical Review E,2002,2665(1):066109.
[11]Holme P,Kim B J,Yoon C N,et al. Attack vulnera⁃bility of complex networks[J]. Physical Review E,2002,65(1):056109.
[12]Latora V,Marchiori M. Efficient behavior of small-world networks[J]. Physical Review Letter,2001,87:198701.
[13]Crucitti P,Latora V,Marchiori M et al. Efficiency of
scale-free networks:error and attack tolerance[J]. Physica A,2003,320:622-642.
[14]Tamronglak S. Analysis of power system disturbances due to relay hidden failures[J]. 1994.
[15]Phadke A G,Thorp J S. Expose hidden failures to pre⁃vent cascading outages in power systems[J]. Comput⁃er Applications in Power,IEEE,1996,9(3):20-23.
[16]张国华,张建华,杨志栋,等.电力系统N-K故障的风险评估方法[J].电网技术,2009,33(5):17-21.
[17]易俊,周孝信.考虑系统频率特性以及保护隐藏故障的电网连锁故障模型[J].电力系统自动化,2006,30(14):1-5.
[18]周建方,唐椿炎,许智勇.事件树、故障树、决策树与贝叶斯网络[J].河海大学学报:自然科学版,2009,37(3):351-355.
[19]刘友波,胡斌,刘俊勇.电力系统连锁故障分析理论与应用(一)相关理论方法与应用[J].电力系统保护与控制,2013,41(9):148-155.
[20]J. Chen,J.S. Thorp,I. Dobson. Cascading Dynamics and Mitigation Assessment in Power System Disturbanc⁃es via a Hidden Failure Model[J]. Electrical Power and Energy Systems,2005,27:318-326.
[21]J.S.Thorp,A.G Phadke,S.H. Horowitz,et al. Anato⁃my of power system disturbances:importance sampling [J]. International Journal of Electrical Power&Energy Systems,1998,20(2):147 52.
[22]CIGRE Task Force 38.03.12. Power system security assessment,a position paper[J]. Electra,1997(175):49-77.
[23]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社有限公司,2006.
[24]Alsac,O.,Stott,B.,Optimal Load Flow with Steady State Security[J]. IEEE Transactions on Power Appa⁃ratus and Systems,Vol. PAS 93,No. 3,1974,pp. 745-751.
(编辑:向飞)
Security Assessment of Power System via a Cascading Model
CHEN Rui1,YANG Yin-guo1,QIAN Feng1,WANG Yan-wei2,FENG Lei2,ZHU Lin2
(1.Guangdong Power Grid Power Dispatching Control Center,Guangzhou510600,China;2. School of Electric Power,South China University of Technology,Guangzhou510641,China)
Abstract:A new method is put forward to assess power system security via a cascading model. Compared with the traditional N-k,the method considers all factors that affect the process of cascading,including the trip of overloading line,the automatic security equipment and the hidden failure of line protection. And the paper focuses on the multiple hidden failure of line protection,and adopts Bayesian network to identify the probability of every fault series. And the paper defines two risk indices,the line risk and the node risk. The simulation on IEEE 30 system proves the effectiveness of the method.
Key words:cascading failure;risk assessment;risk indices
通信作者:朱林,男,1979年生,博士,副教授。研究领域:电力系统稳定与控制。
作者简介:第一陈睿,女,1989年生,广东广州人,硕士。研究领域:电网运行策划、风险管控。
收稿日期:2015-05-05
DOI:10. 3969 / j. issn. 1009-9492. 2015. 11. 032
中图分类号:TM727
文献标识码:A
文章编号:1009-9492 ( 2015 ) 11-0123-06

