取向排列丝素蛋白/聚己内酯复合纳米纤维膜的双轴向拉伸性能
王敏超,熊 杰,2
(1.浙江理工大学材料与纺织学院,浙江杭州 310018;2.浙江理工大学先进纺织材料与制备技术教育部重点实验室,浙江杭州 310018)
静电纺丝纳米纤维膜具有孔隙率高、比表面积大等特点,在组织工程领域有很大的使用价值[1-2],特别是静电纺丝取向排列的纳米纤维膜,在组织工程等领域占有明显的优势[3-5]。在实际应用中,膜材料多向受力,其力学性能非常复杂,目前利用单轴拉伸研究静电纺丝纳米纤维膜材料的力学性能有一定的局限性[6-7],特别是其各向异性的特点更为研究增加了难度,因此,模拟静电纺丝纳米纤维膜材料多种受力方式并研究其力学性能显得尤为必要。
目前双轴向力学性能研究主要集中在织物及工程材料领域。徐艳华等[8]以不同衬纱方式编制织物增强体,对所得复合材料进行双轴拉伸测试,结果表明,材料弯曲性能与编织方式有关,弯曲负荷-伸长率曲线均表现出一定的塑性破坏特征。Amit Rawal等[9]探究了非织造土工布的双轴拉伸力学性能发现,在双轴拉伸作用下,纤维从无规排列趋向于取向排列结构,从而使试样的力学性能表现出各向异性。倪静等[10]对PVC建筑膜材料在7种应力比下进行双轴拉伸试验,推导了经纬向应变之间的关系,并结合建筑膜材料已有理论模型,对膜材料双轴向弹性常数进行了分析。在生物领域,已有Shinghwa Lu等[11]在小肠黏膜支架黏附上肌源性细胞前后,用双轴拉伸方法测试了支架材料环向及径向的面应变发现,肌源性细胞的增殖可使小肠黏膜支架面应变明显增大。然而针对作为组织工程支架的静电纺纳米纤维膜的双轴力学性能研究还较少。
本文研究了静电纺丝取向排列的丝素蛋白/聚己内酯(SF/PCL)丝共混复合纳米纤维膜的双轴向力学性能,并根据拉伸曲线建立数学模型,为深入建立本构模型得到大量实验数据,以期为静电纺丝纳米纤维膜组织工程支架的设计与应用提供参考。
1 实验部分
1.1 实验材料与仪器
再生丝素蛋白(SF),自制;聚己内酯(PCL),Mn=80000,深圳光华伟业有限公司;六氟异丙醇(HFIP),纯度99%,盐城冬阳生物制品有限公司;FC60P2型高压电源,美国 Glassman公司;KDS100型微量注射泵,美国KDS Scientific Inc;滚筒,自制,直径为9 cm。
1.2 静电纺丝试样制备
将SF与PCL按质量比为25∶75溶于HFIP中,配成质量分数为6%的SF/PCL纺丝液,于磁力搅拌器上搅拌12 h,得到透明溶液。静电纺丝参数为:电压15 kV、接收距离12 cm、纺丝流率0.01 mL/min,接收滚筒转速设置为:0、2.35、4.70、7.05、9.40、11.75 m/s。所得SF/PCL纳米纤维膜置于真空干燥箱中静置备用。
1.3 静电纺丝纳米纤维膜形貌表征
用日立S4800场发射扫描电镜FE-SEM观察静电纺丝SF/PCL纤维的形态;用Image-Pro Plus图像分析软件测量纤维直径,样本数为100。
基于FE-SEM图像,使用MatLab软件对静电纺纳米纤维排列情况进行统计。对扫描电镜照片进行二值化处理,设定图像下边缘线为基准线,测量纤维逆时针旋转至与基准线平行时所需角度θ,如图1所示,样本数为180。

图1 图像处理效果Fig.1 Results of image processing
1.4 静电纺丝纳米纤维膜双轴拉伸性能测试
采用日本加多公司KSM-BX5450ST型双向拉伸试验仪对静电纺丝纳米纤维膜进行双轴循环拉伸,实验装置如图2所示。
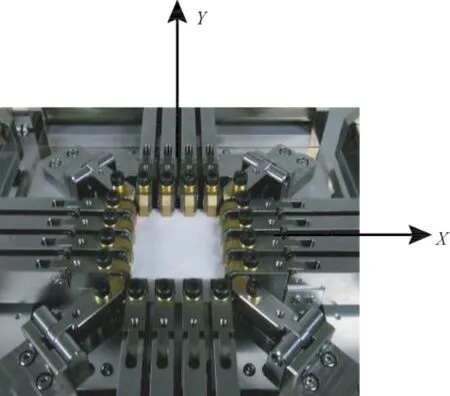
图2 KSM-BX5450ST型双向拉伸试验仪测试示意图Fig.2 Schema of KSM-BX5450ST compact biaxial tensile tester
图中默认垂直滚筒转动方向为X、沿滚筒转动方向为Y,裁剪尺寸为60 mm×60 mm,夹持距离为50 mm,如图2所示放置试样,X向、Y向拉伸力量程均为5 N,拉伸速率均为10 mm/min,拉伸变形量为6 mm,对试样进行3次循环拉伸。
2 结果与讨论
2.1 静电纺丝SF/PCL纳米纤维膜的形貌
图3示出静电纺丝SF/PCL纳米纤维膜的扫描电镜照片,收集滚筒转速分别为 0、2.35、4.70、7.05、9.40、11.75 m/s。当收集滚筒转速为0 时,纳米纤维呈无规排列,直径为(643±107)nm;随着收集滚筒转速增大,纳米纤维排列有序程度提高,纤维直径呈减小趋势,当收集滚筒转速为11.75 m/s时,直径为(422±55)nm。这是因为在纺丝过程中,纤维不仅受到电场力的作用,同时受到滚筒转动引起的牵伸作用,因此,在电压一定的条件下,滚筒转速增大,牵伸力提高,纤维直径减小。

图3 不同滚筒转速下收集的静电纺SF/PCL纳米纤维膜的形貌Fig.3 SEM images of electrospun SF/PCL nanofibers collected at different rotating speed
为定量表征静电纺丝纤维排列的有序程度,用MatLab软件进行统计分析,得到不同滚筒转速下收集的纤维排列分布图,如图4所示,横坐标为纤维逆时针旋转的角度θ,纵坐标为该角度对应的纤维数量占总纤维数量的比例。收集滚筒转速为0时,纤维在各个角度都有分布,排列杂乱无序;收集滚筒转速为7.05 m/s时,分布在20°~60°区域的纤维占主体,呈现出较明显的有序排列;收集滚筒转速增大,纤维分布范围变窄。在6个试样中,当转速为11.75 m/s时,纤维分布最集中,排列取向程度最高。
2.2 静电纺丝纳米纤维膜的双轴拉伸性能
图5、6示出6种不同收集滚筒转速的试样在双轴循环拉伸下的拉伸负荷-伸长率曲线。图5为X向曲线,图6为Y向曲线。从拉伸负荷-伸长率曲线可看出,静电纺丝有序排列的纳米纤维膜材料在双轴拉伸下有如下特性:1)非线性。拉伸负荷与伸长率之间为非线性关系,其非线性程度和拉伸次数有关。循环拉伸次数越多,二者非线性程度越低;2)非弹性。静电纺丝膜材料在循环拉伸作用下,拉伸段与回复段曲线不重合。随着拉伸次数增加,拉伸段曲线与回复段曲线逐渐接近;3)各向异性。静电纺丝膜材料在各向变形一致的条件下,X向与Y向具有不同的力学曲线,并且收集滚筒转速越大,试样各向异性的特征越明显。结合图3纤维FE-SEM图可知:收集滚筒转速越高,所得纤维直径越小,排列越规整,Y轴方向中受力纤维越多,试样能承受的最大拉伸负荷则越大;而X轴方向上,主要是纤维之间摩擦受力,收集滚筒转速越高,纤维排列越规整,纤维间缠结越少,摩擦力越小,试样的最大拉伸负荷则越小。
2.3 双轴拉伸曲线拟合
与第1次循环曲线相比,第2次循环曲线非线性程度显著降低,第3次循环与第2次差别并不明显,本文根据第2次循环时拉伸段的拉伸负荷-伸长率曲线建立数学模型,对第3次循环时拉伸段数据进行验证。为分析SF/PCL纳米纤维排列有序性与其在循环拉伸作用下力学性能的关系,根据拉伸段曲线的变化趋势,用二次方程进行回归拟合为

图4 不同滚筒转速下收集的静电纺丝SF/PCL纳米纤维排列取向分布图Fig.4 Orientation distribution of electrospun SF/PCL nanofibers collected at different rotating speed
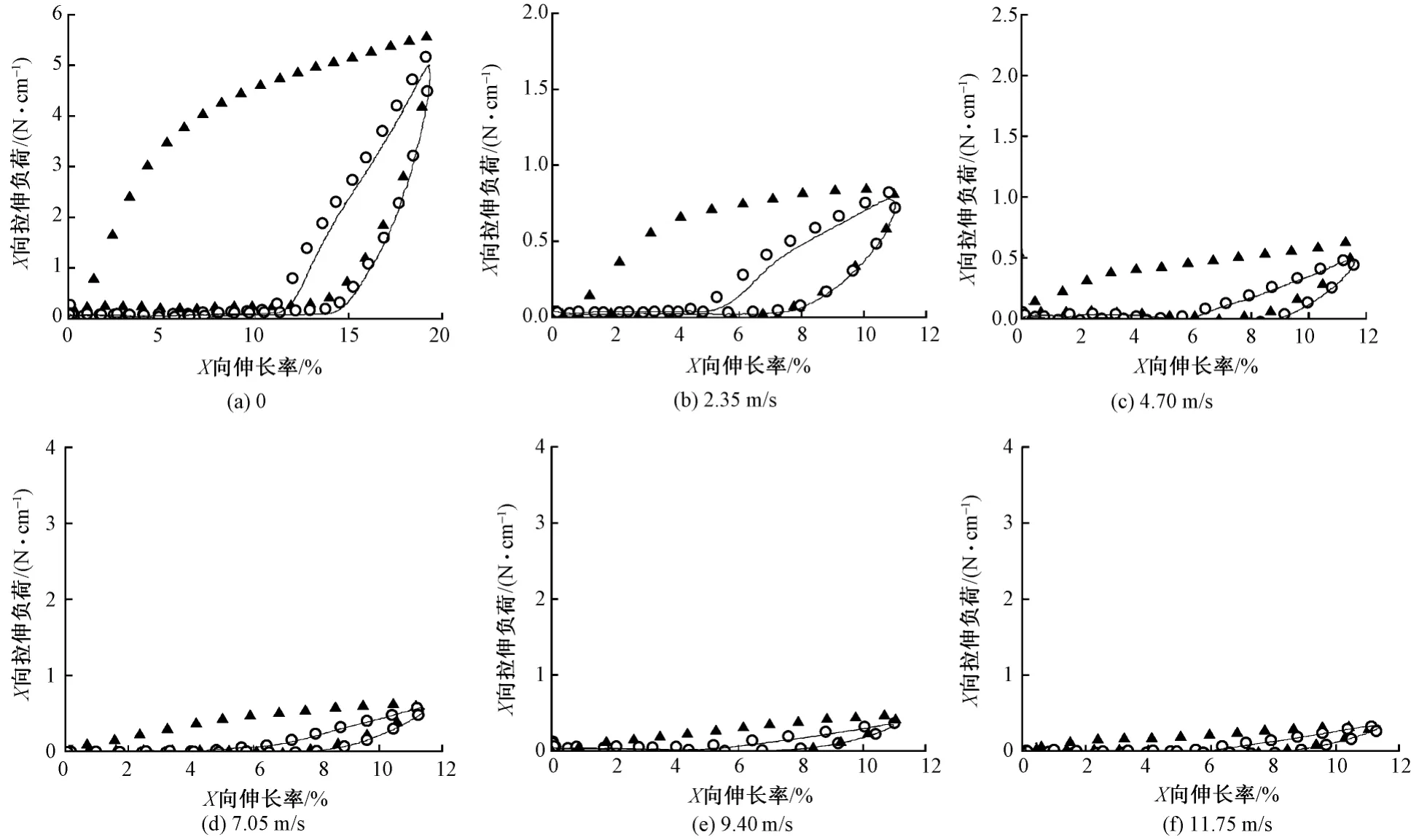
图5 静电纺SF/PCL取向排列纳米纤维膜的双轴循环拉伸负荷-伸长率曲线(X向)Fig.5 Biaxial tensile loading-stretch rate curves of electrospun SF/PCL orientated nanofibrous membranes under cyclic tensile loads(X)

式中:σ为拉伸负荷;ε为伸长率;A、B、C为回归系数。
以Y轴方向为例,图7示出了A、B、C随收集滚筒转速S变化的趋势,并用指数函数进行拟合。从图中各回归系数的变化规律可见,随着收集滚筒转速增大,回归系数A、C有增大的趋势,而B则呈减小的趋势。

图6 静电纺SF/PCL取向排列纳米纤维膜的双轴循环拉伸负荷-伸长率曲线(Y向)Fig.6 Biaxial tensile loading-stretch rate curves of electrospun SF/PCL orientated nanofibrous membranes under cyclic tensile loads(Y)
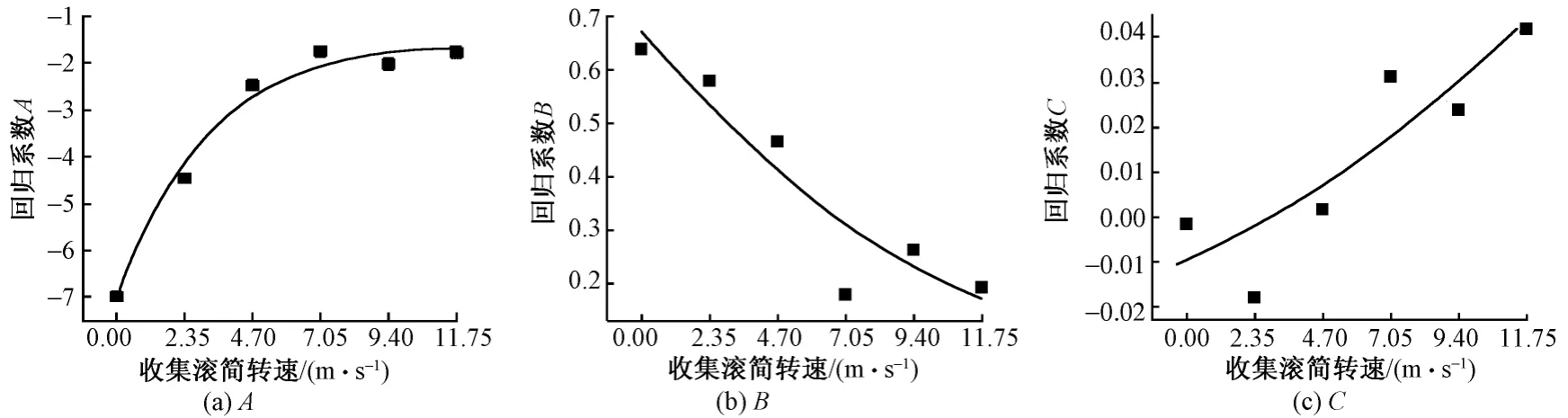
图7 SF/PCL纳米纤维膜Y轴向第2次拉伸的回归系数A、B、C与收集滚筒转速S的关系Fig.7 Relationship between rotating speed(S)and regression coefficient(A,B,C)of electrospun SF/PCL nanofibrous membranes on second drawing
对A、B、C的变化规律进行拟合,可用以下公式描述第2个循环拉伸段A、B、C与转速 S之间的关系:

式中:α、β、φ为指数函数拟合曲线系数,如表 1所示。
于是可得,试样第2次循环时拉伸段有
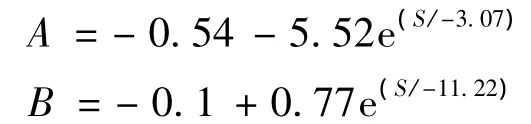
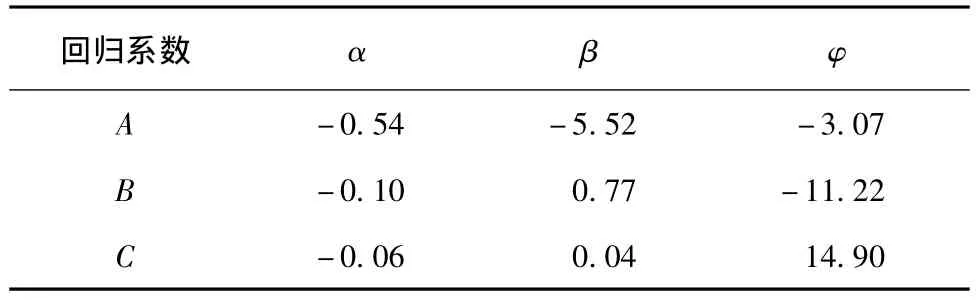
表1 图7拟合曲线系数α、β、φTab.1 Coefficient of fitting curve
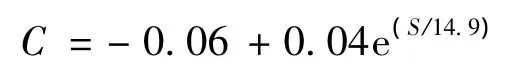
因此,静电纺丝有序排列的SF/PCL复合纳米纤维膜在双轴拉伸作用下,Y向拉伸段的拉伸负荷-伸长率关系模型可由下式描述:

以收集滚筒转速为4.70 m/s的试样为例,运用该数学模型进行验证得到拉伸负荷-伸长率曲线b,与第3次循环时拉伸段的实验数据进行比较,如图8所示,验证曲线b与实验曲线a趋势一致,数值相差较小,可得出式(1)、(2)的假设较为合理。
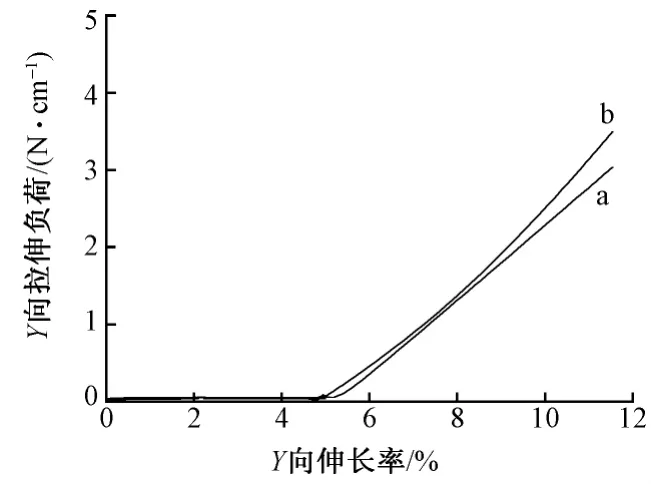
图8 静电纺SF/PCL取向排列纳米纤维膜的双轴循环拉伸段的拉伸负荷-伸长率曲线Fig.8 Biaxial tensile load-stretch rate curves of electrospun SF/PCL orientated nanofibrous membranes under cyclic tensile loads
3 结论
利用扫描电镜及MatLab软件研究了静电纺丝取向排列的SF/PCL纳米纤维的形貌,并通过双轴循环拉伸实验,对静电纺丝膜在双轴拉伸作用下的力学性能进行了研究,得到以下结论:1)收集滚筒转速越大,静电纺丝SF/PCL纳米纤维直径减小,纤维排列有序性提高。2)静电纺丝取向排列的SF/PCL纳米纤维膜具有非线性、非弹性、各向异性的力学性能。3)对双轴循环拉伸曲线进行拟合,建立了数学模型σ=A+Bε+Cε2。经验证,运用该数学模型所得拟合曲线与实验曲线一致性较高。
[1] 常怀云,许淑燕,熊杰,等.静电纺PAN纳米纤维多孔膜的微观结构与过滤性能[J].纺织学报,2011,32(9):1-4.CHANG Huaiyun,XU Shuyan,XIONG Jie,et al.Microstructure and filtration properties of electrospun PAN nanofibrous porous membrane[J].Journal of Textile Research,2011,32(9):1-4.
[2] LIU Haifeng, LI Xiaoming, ZHOU Gang, etal.Electrospun sulfated silk fibroin nanofibrous scaffolds for vascular tissue engineering[J].Biomaterials,2011,32:3784-3793.
[3] 郑鑫,廖桂英,仰大勇,等.有序电纺纤维膜的制备方法及在组织工程中的应用进展[J].高分子材料科学与工程,2011,27(8):181-184.ZHENG Xin,LIAO Guiying,YANG Dayong,et al.Preparation of aligned electrospun fibrous membranes and their applications in tissue engineering[J].Polymer Materials Science and Engineering,2011,27(8):181-184.
[4] SCHNELL E,KLINKHAMMER K,BALZER S,et al.Guidance of glial cell migration and axonal growth on electrospun nanofibers of poly-e-caprolactone and a collagen/poly-e-caprolactone blend[J].Biomaterials,2007,28(19):3012-3025.
[5] XIN X, HUSSAIN M, MAO JJ. Continuing differentiation of human mesenchymal stem cells and induced chondrogenic and osteogenic lineages in electrospun PLGA nanofiber scaffold[J].Biomaterials,2007,28(2):2335-2357.
[6] URSZULA Stachewicz,ILKER Peker,WEI Tu,et al.Stress delocalization in crack tolerantelectrospun nanofiber networks[J].Applied Materials Interfaces,2011,3:1991-1996.
[7] LIN Jiantao, LI Caihong, ZHAO Yi, et al. Coelectrospun nanofibrous membranes of collagen and zein for wound healing[J].Applied Materials Interfaces,2012,4:1050-1057.
[8] 徐艳华,袁新林.双轴向衬纱纬编玄武岩纤维复合材料弯曲性能[J].复合材料学报,2013,30(2):233-239.XU Yanhua, YUAN Xinlin. Bending properties of biaxialweft-knitted basalt fiber fabric reinforced composites of different ways of inserted yarn[J].Acta Material Composites Journal,2013,30(2):233 -239.
[9] AMIT Rawal, ADITYA Kochhar, ASHISH Gupta.Biaxialtensile behavior of spunbonded nonwoven geotextiles[J].Geotextiles and Geomembranes,2011,29:596-599.
[10] 倪静,罗仁安,陈有亮,等.建筑膜材料在双轴拉伸作用下的特性[J].工程力学,2009,26(6):100-104.NIJing, LUO Renan, CHEN Youliang, etal.Characteristics of architectural membrane materials under biaxial tensile loads[J].Engineering Mechanics,2009,26(6):100-104.
[11] SHINGHWALu, MICHAELSSacks, STEVEY Chung,et al.Biaxial mechanical properties of musclederived cell seeded small intestinal submucosa for bladder wall reconstitution[J].Biomaterials,2005,26:443-449.

