织物组织的数字化表达及信息织物设计
骆晓蕾,敖利民,王欢欢,吕小娇,熊梦依,汪宴梅
(嘉兴学院材料与纺织工程学院,浙江嘉兴 314000)
机织物是由经纱和纬纱2个系统的纱线交织形成的。经纱的运动控制有2种形式:单根经纱控制和经纱综框分组控制,单经控制即每根经纱的升降运动单独控制,一般用于织造具有复杂交织规律的大提花织物;综框分组控制即将经纱分为若干组,每组经纱由一片综框控制其升降运动,用于织造交织规律比较简单的原组织、变化组织和小提花等织物,综框片数越多,可织造的织物组织越复杂[1]。
综框控制织造织物的交织规律,即织物组织可用织物组织图来表示,也可用织物组织的规范命名,即符号加文字描述的方式来表示[2]。
现代织机采用电子提综装置控制综框的升降,这就需要将织物交织规律转化为数字信息控制提综顺序。从这个角度来看,织物交织规律的组织图表示方法虽可直观表示织物的交织纹理效果,但不便于转化为数字信息,需要较为复杂图像识别软件来实现;而符号加文字描述的表示方法虽表达简洁,但在转化为控制综框运动的数字信息时,必须先将其转化为图形信息,然后再转化为数字信息[3]。
织物组织图是机织物交织规律设计的基础,但为简化织物组织图转化为电子提综数字信息的算法难度,需要简化织物交织规律的表达方式。
本文在讨论织物组织数字化表达方法的基础上,进一步研究利用织物组织数字化表达的逆过程,将数字串和字母串转化为织物组织的方法,赋予织物组织表达隐含数字信息的可行性。
1 织物组织数字化表达与逆转化
1.1 织物组织的二进制数字化表达
以综框分组控制经纱的运动,在经纱形成梭口时,综框只有2种状态:在上或在下,这一特征可用二进制1和0这2种状态来表示[4]:1表示综框在上,其控制的经纱在布面上形成经组织点;0表示综框在下,其所控制的经纱在布面上形成纬组织点。这样,在织入1根纬纱时所有的综框状态即可构成一个二进制数:综框的总片数决定了该二进制数的位数,有多少片综框,该二进制数就有多少位,每片综框与该二进制数位形成一一对应关系;每一数位的状态,1或0,即表达该数位对应的综框的升降状态,在上或在下。假设某织物采用5片综织造,织入某根纬纱时5片综框的状态为自机前向机后第1片综在上,第2、3片综在下,第4片综在上,第5片综在下,则可用二进制数10010表示,该二进制数最左一位表示第1片综,相应地最右一位表示第5片综。
按照这一表示方法,一个完整的织物组织图即可用一组二进制数来表示:将织物组织图的每一横行(即织入1根纬纱时所有综框状态)对应为一个二进制数,该二进制数所具有的位数等于经纱循环数,每一数位的值取决于其所对应的组织点为经组织点还是纬组织点,经组织点记为1,纬组织点记为0。这样可将织物组织图自上而下转化为一组二进以图1所示的经山形斜纹组织图为例,它有10行、18列,即由10×18个组织点组成,织造该组织织物需将经纱分为18组穿在18片综上,织入10根纬纱完成一个组织循环。将该组织图转化为二进制数组进行表达,需要10个二进制数,组织图自上而下第1横行,即织入第10根纬纱时综框状态对应的二进制数为000101011111010100,同理织入第9根纬纱时综框状态对应的二进制数为001010111011101010,以此类推,织入第1根纬纱时综框状态对应的二进制数为100010101110101000。这样,该组织即可表达为由 10个二进制数组成的数组(000101011111010100,001010111011101010,…,100010101110101000)。二进制数与综框状态的对应是唯一的,由二进制数的位数和个数可直观反映组织循环经纱数和纬纱数。该数组也可用矩阵方式进行表达[6-7]。制数,二进制数的数量与纬纱循环数相等[5]。

图1 经山形斜纹组织图Fig.1 Weave pattern of warp reverse twill
1.2 织物组织的十进制数字化表达
当经纬纱循环数都不大时,为简化表达方法,可进一步将二进制数转化为十进制数。由于十进制数不能直观反映二进制数的位数(需要转换计算),为直观表达组织循环的特征,需要标示出织造综框片数。以图2所示的5枚经面缎纹组织为例,其二进制表达方法为(11011,11110,10111,11101,01111),进一步用十进制数表达方法可表示为5(27,30,23,29,15)[8],十进制数的个数表示纬纱循环数,而括号外的5则表示织造所用综片数,即该织物组织采用5片综织造。

图2 5枚经面缎纹组织图Fig.2 Weave pattern of five-shaft warp stain
1.3 织物组织数字化表达的逆转化还原
将数字表达的经纬纱交织规律,无论是二进制还是十进制,还原为织物组织非常简单,经纬纱循环数可由二进制数的位数(或十进制表示法标明的综片数)和数组所含二进制数(或十进制数)的个数来确定,再将每个二进制数(十进制数先转化为二进制数)各数位按其数值1或0对应为经、纬组织点,自上而下依次排列即可。如按十进制表达的织物交织规律4(7,14,13,11),该织物组织经纱循环数为4(括号外标明),纬纱循环数为4(4个十进制数),将4个十进制数转化为4位二进制数并自上而下排列,得到二进制组织矩阵,如图3(a)所示。将1和0分别对应为经纬组织点,即可得还原组织图,如图3(b)所示为3上1下右斜纹组织。
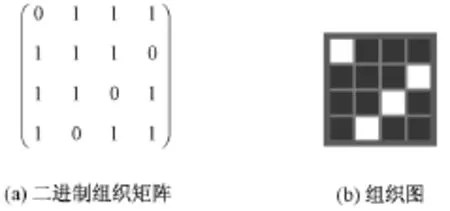
图3 斜纹组织图Fig.3 Weave of twill.(a)Binary weave matrix;(b)Weave pattern
由此可见,以二进制数组表达织物经纬交织规律,可涵盖全部织物交织规律信息,简单且易于相互转换,可简化织物经纬交织规律信息的表达、传送与转换,对于电子提综装置控制系统的设计也具有一定工程意义。对于复杂组织,可参照建立相应的表达规则进行表达,双层织物可用二维数组进行表达。
2 数字信息织物设计
织物组织数字化表达的一个重要的启发是,任何数字化信息均可转化为织物组织,在拓展织物设计范围的同时,赋予织物表达数字信息特征的能力。
织物组织可转化为数字信息进行表达,而其还原过程则可将数字信息逆转化为织物组织,这意味着单独运用逆转化过程,可将任何数字信息转化为织物组织。由数字信息转化成的织物组织,具有不同于现有织物组织设计方法生成的任何织物组织的特征,同时,由具有特定涵义的数字信息转化而成的织物组织,可赋予织物承载隐含数字信息的功能。
数字信息包括直接由数字串表示的信息和可转化为数字串表示的信息2种。直接由数字串表示的信息如各种身份证号、日期、条形码等数字信息码;可转换为数字串的信息包括非数字的其他字符,如英文词汇、汉语拼音等,这些字符可按照一定的规则转化为数字信息。本文只讨论将直接数字信息和英文字母信息转化为织物组织的方法。
2.1 数字串信息转化为织物组织
数字串信息由数字0~9组成,要把数字串信息转化为织物组织,可将数字串的每一位转化而成的二进制数,视为引入1根纬纱时的提综状态。数字串的长度(位数)即为织物组织的纬纱循环数;由于单个数位最大的十进制数为9,而其对应二进制数为1001,位数为4,因此数字串转化为织物组织的最大经循环数(所用综片数)为4,故可用4片综织数字串转化成的织物组织。
如某产品的条形码为9787506414937,欲将其转化为织物组织,首先可确定其经纱循环数为4,纬纱循环数为13(该数字串有13位);然后将每位数字转化为二进制数,并自上而下排列,如图4(a)所示。再将数字1对应为经组织点,数字0对应为纬组织点,即可得织物组织如图4(b)所示。

图4 条形码对应的二进制组织矩阵及织物组织图Fig.4 Corresponding binary weave matrix(a)and weave pattern(b)of barcode
2.2 英文字母信息转化为织物组织
构成字母信息的英文字母共有26个,可先将A~Z共26字母按照一定的对应规则对应为26个十进制数字,由此可将字母串转化为数字串,再将相应数字转化为二进制数,最终转化为织物组织。
本文以A~Z 26个英文字母对应为1~26十进制数字为例,由于最大十进制数26对应的二进制数为11010,为5位二进制数,因此,用5片综即可织造由英文字母构成的字符串转化成的织物组织,该组织的经纱循环数为5,纬纱循环数为字符串的长度。当将拼音信息转化为织物组织时,由于拼音的构成除了字符串之外还有声调信息,在构造织物组织时还要将声调加入到织物组织中。如前所述,字符A~Z对应的最大十进制数是26,而5位二进制数对应的最大二进制数为11111,即十进制的31,中文声调只有“阴、阳、上、去”4个,因此可用十进制数27~30分别对应声调的第1声到第4声。在生成数字串时,以声调作为字音的头。
如拼音信息 TAXUEXUNMEI(踏雪寻梅),由11个英文字母组成,由于由4个字构成,每个字有1个声调,4个字的声调分别为四声、三声、二声、二声,以声调信息为每个字音串的头,可转化成经纱循环数为5,纬纱循环数为15的织物组织,即(30,20,1,29,24,21,5,28,24,21,14,28,13,5,9),其中 30、29、28、28就分别表示每个字的声调。将每个十进制数转化为二进制数并自上而下排列,如图5(a)所示。再将数字1对应为经组织点,数字0对应为纬组织点,即可得织物组织如图5(b)所示。

图5 拼音信息TAXUEXUNMEI对应的二进制组织矩阵与织物组织图Fig.5 Corresponding binary weave matrix(a)and weave pattern(b)of alphabetical information TAXUEXUNMEI
2.3 数字信息织物的可织性及其实现
任何数字串和字母串都可按上述方法转化为织物组织,但任何织物组织都存在可织性问题,并不是所有的织物组织都可上机织造。影响织物可织性的因素主要有2个:1)是否存在有经纱或纬纱不能织进去的情况,即若在一个完整的织物组织中,存在行(纬向)或列(经向)均为纬组织点或经组织点,则其对应的经纱或纬纱未与纬纱或经纱形成交织,则不可织;2)各片综框上经纱的交织次数是否存在较大差异,造成实际织造时各片综经纱张力产生较大差异,织造不能正常进行。经验数据表明,一个组织循环内各纬纱之间的最多经组织点数与最少经组织点数之比不超过2倍,才能基本做到织机正常运转[9-10]。
应该说,上述2种情况在数字信息转化成的织物组织中出现的概率都是比较大的。
如图4所示的条形码织物组织,由于数字0对应的4位二进制数为0000,对应的织物组织中该纬所对应的综框状态为4片综全部在下,因此不能形成交织。对于数字串而言,只要出现数字0,就会出现这种情况。
如图5所示的拼音信息织物组织,自左至右第1片综到第5片综上的经纱在一个组织循环中的经纬交织次数(沿经向经纬组织点转换次数)分别为4、4、4、2、4,第 4 片综上的经纱与纬纱的交织次数明显少于其他4片综,且各纬之间的最多经组织点数与最少经组织点数之比为3。在织造时,该片综会由于交织次数少而造成经纱张力变小并逐渐累积[2],导致织造不能正常进行。
解决数字信息转换而成的织物组织可织性问题的方法,可依据不同的情况采用不同的措施。对于数字串信息,其中不可避免地会经常出现数字0,造成纬纱不能织入,需要一个具有普遍意义的方法加以解决。实际上,由于单个数位最大的十进制数为9,其对应二进制数为1001,而4位二进制数最大可表示的数为1111,还有5个数(1010~1110)没有用到,这里不妨约定用1010表示数字0,即当数字串信息中出现0时,用1010代替,而不用0000。这样即可解决纬纱不能织入的问题。如图4所示条形码织物组织,将数字0对应的0000用1010替换,即可简单解决对应数字为0的纬纱不能形成交织的问题,如图6所示。
出现经纱织不进的概率很低,如果出现这种情况只能用其他组织与信息组织联合,沿经向将信息组织分割开来,以解决不可织问题。

图6 改进后条形码信息组织Fig.6 Modified weave pattern barcode information weave
解决各片综由于交织次数差异而引起的张力差异导致的可织性问题,可采取双轴织造的方法,将交织次数相差较大的综片的经纱分别进行张力控制。也可采用解决经纱织不进时的组织联合方法,即组织上下联合的方法。如图5所示的拼音信息组织,在该组织上下添加各4根纬纱的平纹组织(如图7所示),则各片综的交织次数差异会显著减少,5片综的交织次数依次为 7、8、7、6、8,因而能较好解决经纱张力差异造成的可织性问题。

图7 平纹与拼音信息联合组织Fig.7 Combined weave pattern of plain weave and alphabetical information weave
2.4 信息组织的标示与分割
信息织物的信息必须具有可识别性。为便于信息的识别,在经纬纱线的选择上要予以注意。对于没有联合其他组织的信息组织织物,每织造一个完整的组织循环,都要用不同特征,最好是不同颜色的经、纬纱,这样就会在织物表面上形成完整、独立而易于区分的信息块。如果信息组织与其他组织联合,信息有可能因为联合组织的引入而混乱。这时,可在信息组织与联合组织交界部分采用色纱或其他特殊纱线加以分割,将信息部分明确标示出来。
图8(a)所示为“方正为人,勤慎治学”生成的织物组织图,8(b)所示为织出的织物实物图,对应十进制数组为(27,6,1,14,7,30,26,8,5,14,28,23,5,9,28,18,5,14,28,17,9,14,30,19,8,5,30,14,26,8,9,28,24,21,5),对应二进制数为(11011,00110,00001,01110,00111,11110,11010,01000,00101,01100,11100,10111,00101,01001,11100,10010,00101,01110,11100,10001,01001,01110,11110,10010,01000,0101,11110,01110,11010,01000,01001,11100,11000,10111,00101)。为便于信息的区隔识别,每个组织循环经纱、纬纱采用了黑、白双色纱线进行织造,织物的每一条块均为1个完整的组织循环,已是一个独立的信息区块。

图8 组织图与织成的织物Fig.8 Weave pattern and fabric sample.(a)Weave pattern;(b)Fabric sample
3 结论
1)机织物经纬交织规律可进行数字化表达,这种表达方法不仅可涵盖织物组织信息,而且简化织物经纬交织规律信息的表达、传送与转换,对于电子提综装置控制系统的设计具有一定工程意义。
2)任何数字信息均可转化为织物组织,由具有特定涵义的数字信息转化而成的织物组织,可赋予织物负载数字信息的功能。
3)由数字串或字母串转化而成的织物组织,可能存在可织性问题,可采用双轴织造、组织联合等方法改变组织的可织性。
4)含有数字信息的织物组织,需要合理利用经纬纱色纱排列或特殊纱线将信息区域明确分割开来,以便于信息的识别与解读。
此外,数字信息织物组织具有与现有规律性织物组织不同的交织规律,会表现出不同的外观特征及性能特征,是对现有织物设计的有效拓展。
[1] 朱苏康,高卫东.机织学[M].北京:中国纺织出版社,2008:193-267.ZHU Sukang,GAO Weidong.Weaving[M].Beijing:China Textile& Apparel Press,2008:193-267.
[2] 蔡陛霞.织物结构与设计[M].4版.北京:中国纺织出版社,2008:29-139.CAI Bixia.Fabric Structure and Design[M].4th ed.Beijing:China Textile& Apparel Press,2008:29-139.
[3] 张瑞林,李志祥.电子多臂提花系统织物组织编程器的分析[J].现代纺织技术,2000,8(1):21 -25.ZHANG Ruilin,LIZhixiang. Analysison weave programmer of electronic dobby system[J].Modern Textile Technology,2000,8(1):21-25.
[4] 二进制[EB/OL].(2013-12-18)[2014-02-08].http://zh.wikipedia.org/zh-cn/%E4% BA% 8C%E8%BF%9B%E5%88%B6.Binary[EB/OL].(2013-12-18)[2014-02-08].http://zh.wikipedia.org/zh-cn/%E4%BA%8C%E8%BF%9B%E5%88%B6.
[5] 姚继明.三原组织的数字化处理初探[J].武汉纺织工学院学报,1999,12(2):75 -77.YAO Jiming.The first probe of the digital treatment of three-elementary weave [J].Journal of Wuhan Textiles Science& Technology Institute,1999,12(2):75-77.
[6] 谢宝珠,张聿,金耀,等.基于组织矩阵移位迭代运算的织物组织设计[J].纺织学报,2010,31(6):37-42.XIE Baozhu,ZHANG Yu,JIN Yao,et al.Fabric weave design based on swift operation and interative operation of weave matrix [J].Journal of Textile Research,2010,31(6):37-42.
[7] 赵良臣,闻涛.旋转组织设计的数学原理[J].纺织学报,2003,24(6):33 -34.ZHAO Liangchen,WEN Tao.Mathematical principles of rotation weavedesign[J]. JournalofTextile Research,2003,24(6):33-34.
[8] 二进制与十进制间的转换方法[EB/OL].(2011-03-08)[2014-02-08].http://www.360doc.com/content/11/0308/14/5327079_99222581.shtml.Conversion method between binary and decimal[EB/OL].(2011-03-08)[2014-02-08].http://www. 360doc. com/content/11/0308/14/5327079_99222581.shtml.
[9] 胡克勤,金关秀.织物设计参数对其可织性的影响[J].纺织科技进展,2010(4):34-36.HU Keqin,JIN Guanxiu.The effect of fabric design parameter on weavability[J].Progress in Textile Science&Technology,2010(4):34-36.
[10] 马芹,刘学锋,王秋霞.利用紧密率判断织物可织性[J].郑州纺织工学院学报,2000,12(4):43 -46.MA Qin,LIU Xuefeng,WANG Qiuxia.Using tightness ratio to judge fabrics weavabihliy [J].Journal of Zhengzhou Textile Institute,2000,12(4):43-46.

