聚芳噁二唑纤维的热降解动力学
杨 潇,周万立,贾二鹏,叶光斗,徐建军
(1.西南大学纺织服装学院,重庆 400715;2.四川大学高分子科学与工程学院,四川成都 610065)
聚芳噁二唑(POD)是一类苯环和噁二唑环交替共轭的芳杂环类聚合物[1]。由于大分子链含有噁二唑环,因此POD具有非常优良的耐热性、热稳定性;同时由于噁二唑环还具有光电效应,是很好的亲电子基团,因此POD在光电材料方面也有很好的应用[2-4]。此外,POD还具有非常良好的成膜成纤性,其制得的纤维在高温滤材、防护制品、绝缘材料等方面均有广泛应用[5-7]。目前,对POD热稳定性的研究主要集中在合成改性方面,即引入不同的官能团,通过TG或DSC来考察POD的热稳定性改变[8-10]。而从热降解动力学的角度来阐述POD热稳定性的基础研究还未见有详细的相关报道,因此,本文采用不同的升温速率,分别运用 Kissinger、Flynn-Wall-Ozawa、Coats-Redfern法研究POD在不同氛围中的热降解动力学。
1 实验部分
1.1 原料
POD纤维,由江苏宝德新材料公司提供,噁二唑环成环率为98.3%。
1.2 测试方法
采用仪器型号为Q600(氮气氛围)和Q500(空气氛围)的美国TA Instrument热失重分析仪。将聚合物样品置于铝制坩埚中,在氮气氛围或空气氛围下,以不同升温速率进行热失重表征,升温范围为20~700 ℃,升温速率分别为5、10、20、50 ℃ /min,样品用量为(5±0.1)mg。
2 动力学研究方法
2.1 Kissinger法
Kissinger法[11]利用不同升温速率下,热失重一次微分曲线的峰值所对应的温度来计算活化能。Kissinger法的基本经验方程为:

式中:β为升温速率,℃/min;Tp为最快热失重速率下的热力学温度,K;E为活化能,kJ/mol;R为气体常数;A为指前因子。以ln(β/)-1/Tp作图,根据斜率和截距可求得E和A。
2.2 Flynn-Wall-Ozawa法
Flynn-Wall-Ozawa法[11]是一种常用的积分方法,其优点是不需引入分解机制函数就可求得分解活化能E,避免了因反应机制假设不当而得到错误的动力学参数,故常用此方法所求的E值来判断其他研究方法的合理性。其基本经验方程为:

对于方程(2),在不同升温速率下,给定一个热失重率α,同一体系的G(α)就是一个恒定值;从热动力学数据中可找到不同升温速率时,给定α所对应的温度T,以lgβ对1/T作图并进行线性拟合,就可得到不同α下的一系列拟合直线,根据拟合直线的斜率即可求得热失重率为α时的活化能E。
2.3 Coats-Redfern法
Coats-Redfern 法[11]为假设 f(α)=(1 - α)n,作一定近似处理后,可得如下方程:
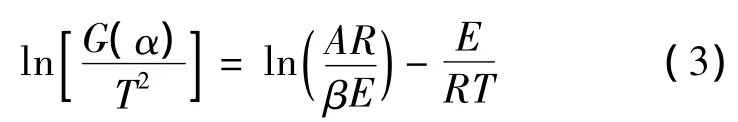
式中,G(α)为分解机制函数的积分形式。
如果已知 G(α),以 ln[G(α)/T2]对1/T作图并进行线性拟合,从拟合直线的斜率和截距即可求得分解活化能E和指前因子A。将常用的热分解机制函数分别带入方程(3)中,计算出各自的E值,再将其与Flynn-Wall-Ozawa法所确定的参数进行比较,从而确定材料降解反应的机制。
3 结果与讨论
3.1 热性能分析
在氮气和空气氛围下以5、10、20、50℃/min升温速率升温时,POD纤维的热失重(TG-DTG)曲线如图1所示。从图1(a)中可看出,在恒速升温及氮气氛围下,POD纤维经历的是一步质量损失过程,最快质量损失速率发生在520~600℃之间,之后失重趋于平缓,最终残炭率在40%左右。随着升温速率的提高,POD纤维的初始热失重温度及最大热失重速率所对应的温度均升高,这是由升温速率增高而引起的热滞后效应。而从图1(b)可看出,在空气氛围下,POD纤维经历的是2步失重过程,最快失重率发生在500~700℃之间,最终残炭率在3%左右。同在氮气氛围下一样,随着升温速率提高,POD各项热分解温度均有向高温方向移动的趋势。通过对比2个图的DTG曲线可看到:在热降解的初始阶段,在氮气和空气氛围下,POD的DTG曲线都非常相近,意味着在此阶段二者的热降解机制可能相似;而在热降解中后期,在空气氛围下,POD会进一步发生降解反应,导致其DTG曲线与氮气氛围下的不同,即两步失重过程。从残炭率也可比较出,在空气氛围下,POD热分解的更加完全。由此可见,空气中的氧对POD的热降解机制有明显影响。
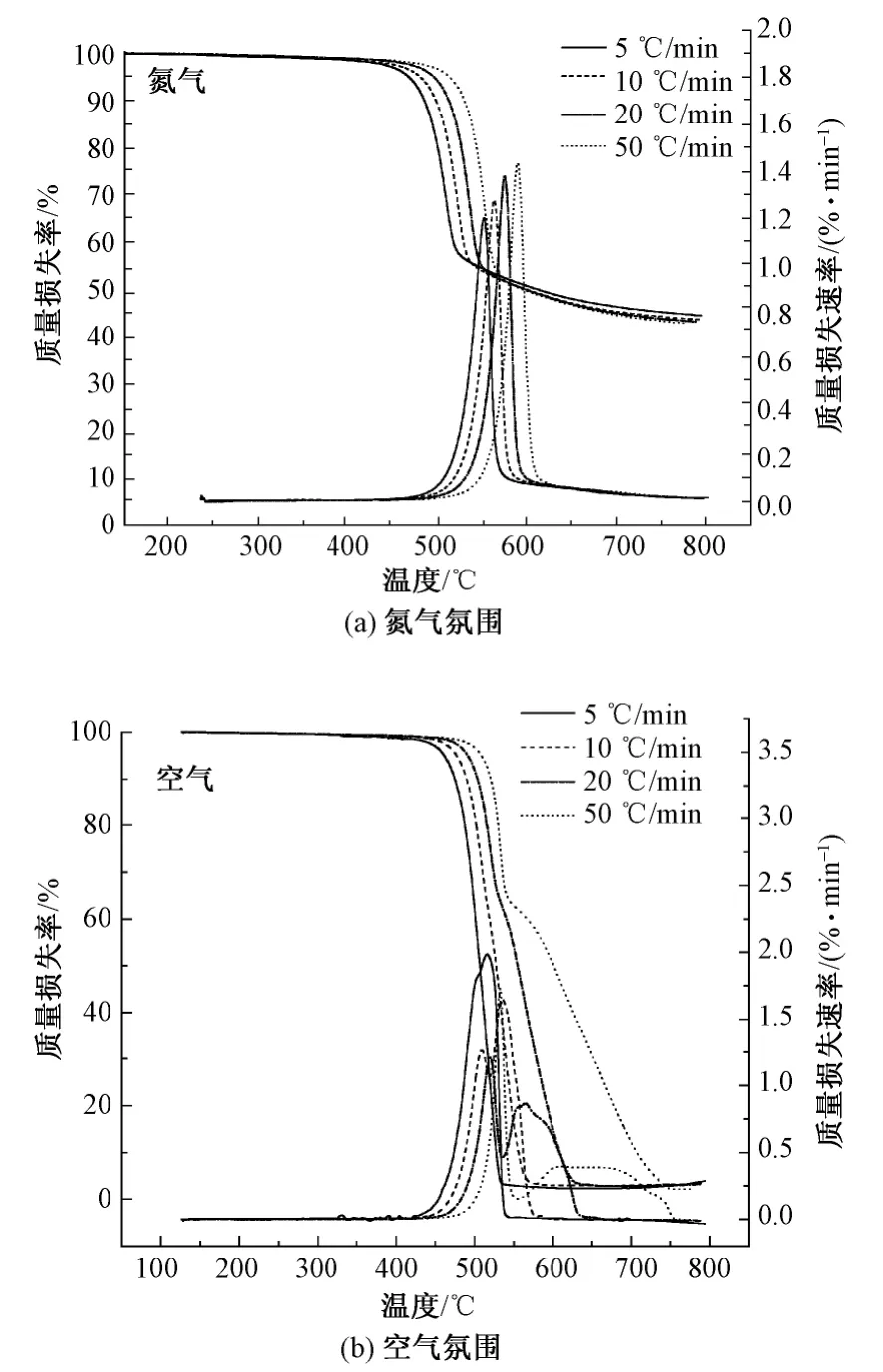
图1 POD纤维在氮气和空气氛围热失重曲线Fig.1 TG/DTG curves of POD in nitrogein(a)and in air(b)
3.2 动力学参数分析
3.2.1 Kissinger法分析
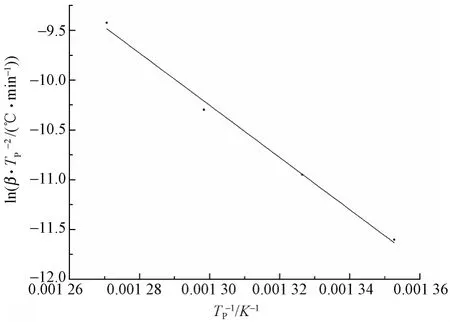
图2 Kissinger法ln(β/)与1/Tp关系图(氮气氛围)Fig.2 Relationship between ln(β/)-1/Tp according to Kissinger method(in nitrogen)
由拟合直线的斜率和截距可计算得到氮气氛围下POD热降解的活化能E和指前因子A,结果见表1。由表可看到,通过 Kissinger方法得到的POD热降解活化能高达277 kJ/mol,这同已有报道的PBO、PPS 等高性能纤维处在同一级别[12-13],说明POD有着非常优异的热稳定性。在空气条件下,由于在第二阶段DTG曲线不规则,运用Kissinger法研究并不适合,因此采用其他二种方法对其研究。

表1 Kissinger法计算得到的活化能E,指前因子A及线性相关系数Tab.1 Activation energy(E),pre-exponentialfactor(A)and correlation coefficients(R)of POD fibers according to Kissinger method
3.2.2 Flynn-Wall-Ozawa法分析
根据Flynn-Wall-Ozawa法的经验方程(2),以lgβ对1/T作图并进行线性拟合,如图3所示。根据拟合直线的斜率可计算得到活化能E,见表2所示。
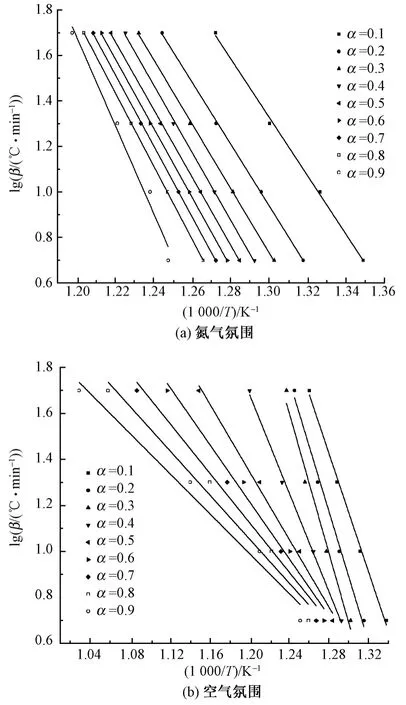
图3 Flynn-Wall-Ozawa法lg(β)与1/T关系图Fig.3 Relationship between lg(β)-1/T according to Flynn-Wall-Ozawa method.(a)In N2;(b)In air
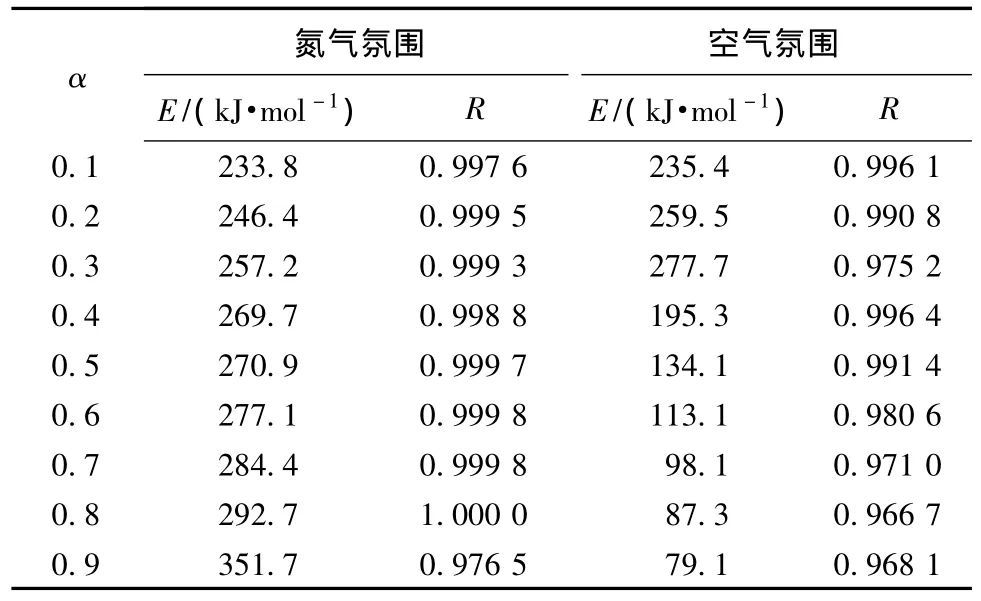
表2 Flynn-Wall-Ozawa法计算得到的活化能E及线性相关系数Tab.2 Activation energy(E)and correlation coefficients(R)of POD fibers according to Flynn-Wall-Ozawa method
从图3可看出,采用Flynn-Wall-Ozawa方法对POD热降解动力学进行分析是比较合适的,各拟合直线的线性相关系数都接近1。并且从斜率求得的热降解活化能E值可发现,当α为0.1、0.2、0.3时,氮气和空气氛围的平均E值分别为245.8 kJ/mol和257.5 kJ/mol,非常相近,进一步说明在POD的初始热降解阶段可能遵从相同的热降解机制。热降解后期,在氮气氛围下,E值逐步有所增加,但是幅度都较小,α为0.9时,E值变化较大,这可能是由于POD炭化的缘故导致热降解行为有所变化;在空气条件下可看到,在热降解中后期,当α为0.4时发生转折,E值变小,并在随后热降解过程中逐步减小,在热降解后期,E值已经低至79.1 kJ/mol。对比2种氛围下POD的热降解动力学数据,可以看到:当聚合物开始发生热降解时,E值相差不大;在中后期,若在氮气条件下,E值逐渐升高,但是升高幅度不大,各拟合直线有较好的平行关系,表明虽然聚合物热降解所需要的能量在逐步增大,但是应该都遵从同一热降解机制;若在空气条件下,因为有氧气的参与,将导致热降解活化能在中后期大大降低,并且在随后的热降解过程中逐步降低,使得聚合物的热降解越来越容易,因此,氧气对降低POD的热降解活化能有重要作用。在中后期的热降解过程中,不同氛围下的热降解行为是不相同的。
3.2.3 Coats-Redfern法分析
为进一步探讨不同氛围下POD的热降解行为,通过Coats-Redfern方法研究二者的热降解机制函数积分形式G(α)(常用G(α)函数见表3),其中用于数据分析的热失重曲线升温速率为10℃/min。表4示出POD纤维在氮气和空气条件下通过Coats-Redfern方法求得的热降解活化能,其中α的热失重区间为0.1~0.3。

表3 常用热分解机制方程(积分形式)Tab.3 Common equations of thermal decomposition mechanism(Integral form)
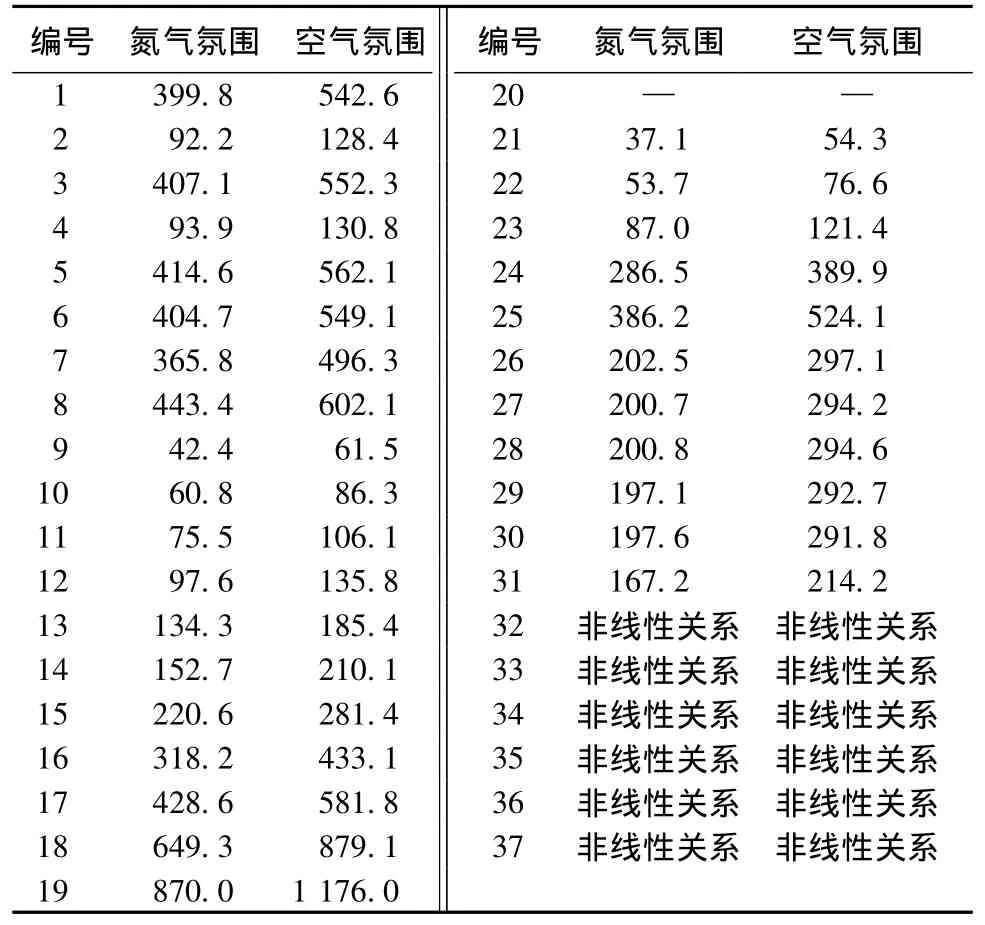
表4 Coats-Redfern法计算得到的活化能E(α为0.1~0.3)Tab.4 Active energy(in nitrogen and air)calculated by Co ats-Redfern method(α=0.1~0.3)kJ/mol
与Flynn-Wall-Ozawa方法求得的E值比较可发现,在氮气条件下,α为0.1~0.3时,Ozawa的平均E值为245.8 kJ/mol,Coats-Redfern法求得的 E值与之最相近的为220.6 kJ/mol,即G(α)=-ln(1-α),其机制为随机成核和随后生长,n=1。而在空气条件下,同样 α为0.1~0.3时,Ozawa的平均E值为257.5 kJ/mol,由表3可看到,与之最相近的E为281.4 kJ/mol,同样为 G(α)= -ln(1-α),因此,在POD初始热分解阶段,无论在氮气还是空气条件下,其热分解机制相同,这与前述的推测相吻合。
表5示出POD纤维在氮气和空气氛围下通过Coats-Redfern方法求得的热降解活化能,其中氮气氛围条件下讨论的α为0.2~0.8,空气氛围条件下讨论的α为0.4~0.9。
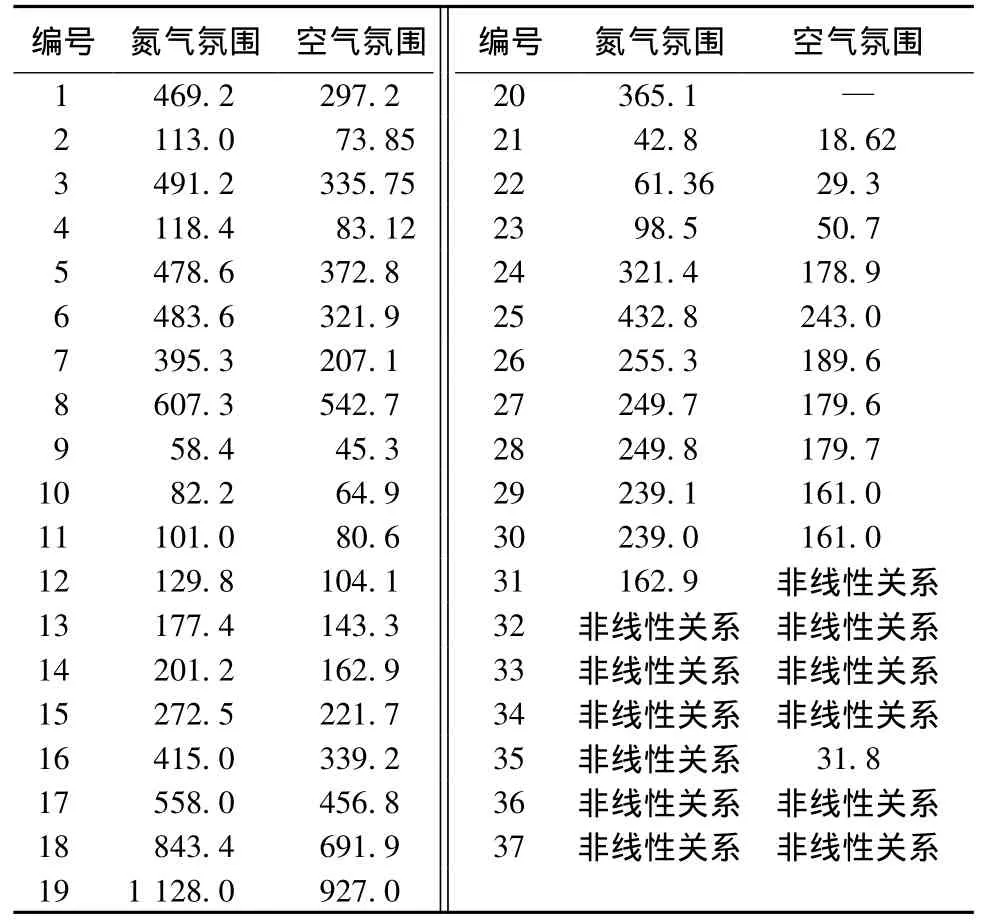
表5 Coats-Redfern法计算得到的活化能ETab.5 Active energy(in nitrogen and air)calculated by Coats-Redfern method kJ/mol
与通过Flynn-Wall-Ozawa方法求得的E值相比较可发现,在氮气氛围条件下,Ozawa的平均E值为271.2 kJ/mol(取 α 为 0.2~0.8),而 通 过Coats-Redfern方法求得的 E值与之相近,为272.5 kJ/mol,仍然为 G(α)= -ln(1 - α)。在空气条件下,Ozawa的平均 E值为117.2 kJ/mol(α为0.4~0.9),而通过Coats-Redfern方法求得的 E值与之相近的为104.1 kJ/mol,即G(α)=[-ln(1-α)]1/2,其机制为随机成核和随后生长,n=0.5。由此可见,POD在不同氛围下热降解时,机制函数均为随机成核和随后生长,但是反应级数有差异:在氮气条件下,级数为1;而在空气条件下热降解中后期,级数由1变成0.5。
4 结论
1)POD纤维具有非常优异的热稳定性,随着升温速率的增加,纤维的初始热降解温度及最快热降解速率温度均增大。氮气氛围下,POD纤维有着较高的残炭率;空气氛围下,POD纤维热降解更加完全。
2)采用 Kissinger法计算得到了氮气氛围下POD纤维的活化能E为277 kJ/mol。
3)采用Flynn-Wall-Ozawa法计算得到了POD纤维在不同氛围下的E值:在氮气氛围下 E在233.8~351.7 kJ/mol之间;在空气氛围下 E在235.4~79.1 kJ/mol之间。在热降解中后期,氧的参与会导致POD纤维热降解活化能降低。
4)通过Coats-Redfern法和Flynn-Wall-Ozawa法的联用计算,得到了POD纤维在不同氛围下热降解机制方程的积分形式:在热降解初期,无论在氮气氛围还是空气氛围,均为G(α)=-ln(1-α),机制为随机成核和随后生长,n=1;在空气氛围下,热降解中后期,G(α)=[-ln(1 - α)]1/2,机制为随机成核和随后生长,n=0.5。
[1] SCHULZ B,BRUMA M,BREHMER L.Aromatic poly(1,3,4-oxadiazole)s as advanced materials [J].Advanced Materials,1997,9(8):601 -613.
[2] SCHULZ B,LEIBNITZ E.Aromatic poly(oxadiazole)snew aspects of their synthesis,structures and properties[J].Acta Polymer,1992,43:343 -347.
[3] FRAZER A H,SWEENY W,WALLENBERGER F T.Poly(1,3,4-oxadiazoles):a new class of polymers by cyclodehydration of polyhydrazides [J]. Polymer Science:Part A,1964,2:1157-1169.
[4] HUANG W,YU W L.New series of blue-light-emitting polymers constituted of 3-alkylthiophenes and 1,4-di(1,3,4-oxadiazolyl)phenylene [J].Chemistry Materials,1998,10:3340-3345.
[5] IMAI Y.Direct fiber formation and fiber properties of aromatic polyoxadiazoles [J]. Applied Polymer Science,1970,14:225-239.
[6] ZHANG ZX, LIW T, XU JJ. Influence of cyclodehydration on formation and properties of poly(pphenylene-1,3,4-oxadiazole)fiber [J]. Plastic,Rubber and Composites,2007,36:343 -349.
[7] 李文涛,张再兴,徐建军.芳香族聚噁二唑纤维的制备极其结构与性能[J].合成纤维,2007(10):31-36.LI Wentao,ZHANG Zaixing,XU Jianjun.Preparation,structure and properties of aromatic polyoxadiazoles fiber[J].Synthetic Fiber in China,2007(10):31 -36.
[8] ZHU S,SCHULZ B,BRUMA M.Comparative study of the thermal properties of related aromatic polyhydrazides and poly(1,3,4-oxadiazole)s [J].Polymers for Advanced Technologies,1996,7:879-887.
[9] 吴萌,张再兴,徐建军,等.间苯二甲酸含量对芳香族聚噁二唑纤维性能的影响[J].高分子材料科学与工程,2009,25(2):97 -100.WU Meng,ZHANG Zaixing,XU Jianjun,et al.Effect of iso-phthalicacid on the properties of aromatic polyoxadiazoles fiber[J].Polymer Materials Science and Engineering,2009,25(2):97-100.
[10] HAMCIUC C, HAMCIUC E, BRUMA M, et al.Poly(1,3,4-oxadiazole-amide)s containing pendent imide groups [J]. Polymers for Advanced Technologies,1996,7:847 -852.
[11] 胡荣祖,史启祯.热分析动力学[M].2版.北京:科学出版社,2001:29-55.HU Rongzu, SHI Qizhen. Kinetic of Thermal Analysis[M].2nd ed.Beijing:Science Press,2001:29-55.
[12] 张敏,唐来安,韩哲文,等.聚亚苯基苯并二噁唑的热分解行为[J].华东理工大学学报:自然科学版,2006,32(1):60 -64.ZHANG Min,TANG Laian,HAN Zhewen, et al.Thermal degradation of poly(p-phenylenebenzobisoxazole)[J].East China University of Science and Technology:Natural Science Edition,2006,32(1):60-64.
[13] 李利君,蒲宗耀,兰彬,等.聚苯硫醚纤维的热降解动力学[J].纺织学报,2010,31(12):4-8.LI Lijun, PU Zongyao, LAN Bin, et al. Thermal degradation kinetics of polyphenylene sulfide fibers[J].Journal of Textile Research,2010,31(12):4-8.

