电网故障下双馈风电机组的转矩特性及对轴系的影响分析

贾 锋，张 琛，蔡 旭，李少林，李 征

(1.上海交通大学，上海200240;2.中国电力科学研究院，北京230009)

0 引 言

传动系统是双馈风电机组中重要的一环，起到传输机械功率和转速变比的作用。由于风电机组传动系统是典型的欠阻尼系统，作用于轴系的气动转矩和电磁转矩的动态变化都可能激发轴系扭振，轴系振荡可能引起机组转速失稳［1］并会造成PCC 点功率波动，另外齿轮箱故障在风机故障造成的机组停机维护中所占比重最大［2-3］，会带来极高的系统运行和维护代价。

电网电压故障会引起发电机端电磁转矩的剧烈波动［4］，打破轴系平衡状态并激发扭振，对风电机组传动系统极为不利，设法降低故障期间电磁转矩对扭振的影响具有重要意义。文献［7］基于空间矢量和正负序分量法分析了转子跨接电阻撬棒(Crowbar)保护电路投入后定转子电流的解析表达式，但是没有分析故障转矩及其对扭振的影响。文献［4］对三相对称故障下双馈机组感应电机运行下的转矩暂态行为进行了分析，但是得出的结论不够全面。

本文全面分析了双馈机组故障下Crowbar 阻值对电磁转矩以及轴系扭振的影响，并通过仿真验证了分析结果。

1 轴系模型和故障下的电磁转矩特性

1.1 轴系模型

由于两质量块模型能反映轴系的扭振动态且精度能够满足要求［12］，因此本文选取该模型为研究对象，采用集中参数建模，模型结构如图1 所示。

图1 中，Tt，Ht，ωt分别为风轮气动转矩、惯性时间常数、转速，Tg，Hg，ωg分别为发电机的电磁转矩、惯性时间常数、转速;φ，ε，Ts分别为传动轴的扭转角度、扭转角速度和扭矩;b，k 分别为传动轴的阻尼系数和刚度系数;Dt，Dg分别为风轮自阻尼和发电机自阻尼，各物理量均折算到低速轴侧并标幺化，得到轴系的状态方程:

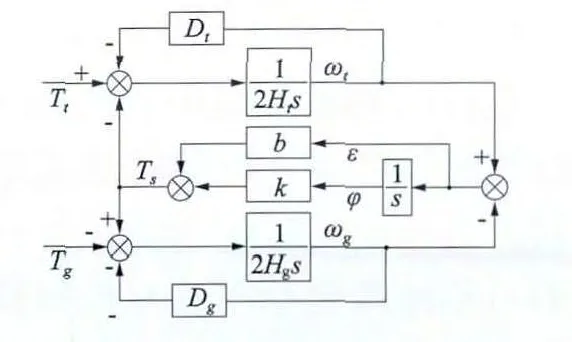
图1 轴系两质量块模型

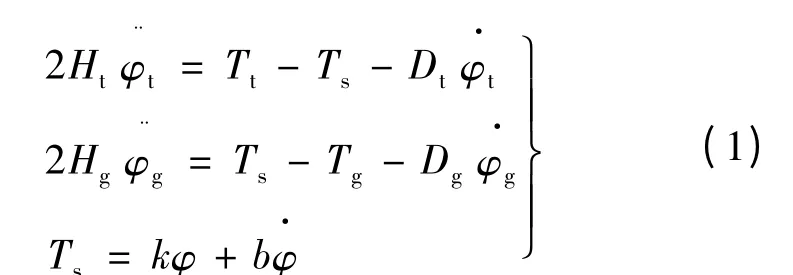
式中:φ=φt-φg为扭转角度。轴系的自然振荡频率［9］:

由于Dt，Dg通常很小，本文忽略这两项的影响，轴系的阻尼衰减因子:

本文所采用的传动链参数:Ht=2.5 s，Hg=0.5 s，b=0.5，k =157.07。计算得到ωn=13.7 rad/s(fn=2.18 Hz)，γ0=0.06。由于阻尼比(ζ=γ0/ωn)远小于1，系统为典型的欠阻尼系统，轴系扭振容易被激发。

1.2 电网故障下的电磁转矩特性

电网故障下轴系扭振的主要激发源是发电机的电磁转矩，因此有必要充分认识故障下的电磁转矩特性。Crowbar 的典型的拓扑电路由三对反并联的晶闸管串接电阻组成，该方案在转子电流超出一定阈值时Crowbar 投入运行、同时转子侧变流器锁闭，从而将转子侧变流器短接。本文以下研究均基于该方案，图2 是在5 s 发生单相短路故障(持续600 ms)的电磁转矩(标幺值)及其频谱分析。

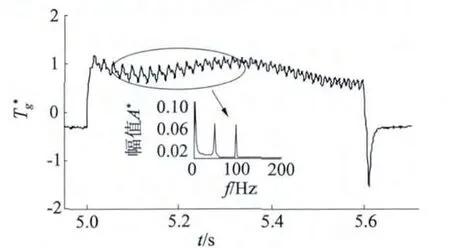
图2 单相短路故障的电磁转矩及频谱分析

扭转角速度ε 是一个能反映轴系扭振的特征量，为了研究电磁转矩暂态响应对扭振的影响，可以列出从扭振的特征量ε 到电网故障下扭振激发源Tg的传递函数:

对该传递函数做bode 图分析，结果如图3 所示。谐振峰对应于轴系自然振荡频率(2.18 Hz)，由于电磁转矩脉动的频率为50 Hz(不对称故障还包含100 Hz 分量)，从bode 图可以看出50 Hz 以上频段的幅频响应幅值很小，这说明相对而言大时间常数的机械扭振问题对转矩高频脉动的感受并不敏感;又由于故障引发的磁链直流分量衰减很快，电磁暂态响应在一到两个周波内基本趋于稳定，因此可以推断故障发生和恢复短时间内的转矩暂态响应以及故障期间转矩的高频脉动对扭振影响较小。

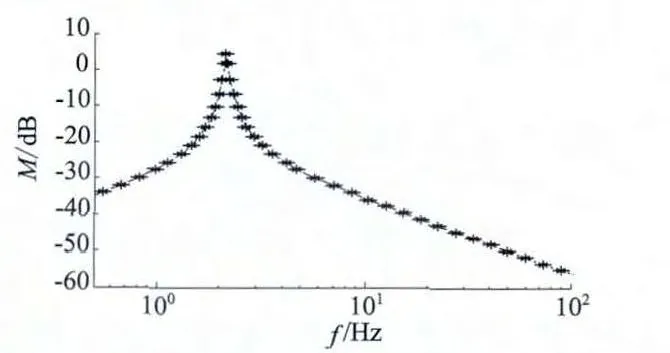
图3 扭转角速度到电磁转矩传递函数的bode 图

由于故障期间电磁转矩的稳态分量相比故障前会发生变化，该变化会导致轴系从一个稳态向另一个稳态过渡，过渡过程通常伴随扭振的发生，因此故障前后电磁转矩稳态值的变化量对扭振的影响较大。

2 减小激振源的扭振抑制措施探究

2.1 Crowbar 阻值选取对轴系扭振的影响

Crowbar 阻值Rcb选取时通常考虑两个限制条件:Rcb要足够大，以限制发电机的转子电流;Rcb不能过大，以避免发电机转子绕组电压过高。根据以上条件可以确定出一个合适的Rcb范围，本文则着重研究在该范围内取值的Rcb对电磁转矩的影响。

根据上节分析，电网故障下Rcb的选取对轴系扭振影响，应当以稳态电磁转矩的分析为主，这里借助于如图4 所示的DFIG 稳态运行等效电路进行分析。

图4 投入Crowbar 的DFIG 稳态运行等效电路

图4 中，Rs为定子电阻;Lσs和Lσr分别为定子漏感和转子漏感;Lm为互感。为简化分析，忽略一些对计算结果影响较小的因素，包括:空间和时间谐波;磁饱和;定子等效电阻。则定子端的输入阻抗:

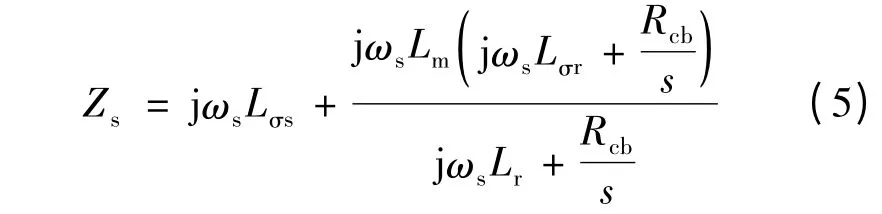
本文首先以发生三相对称故障为例进行分析，假设电压跌落深度为p，在静止坐标系下，借助于图4 的稳态运行等效电路，可求出稳态电流:

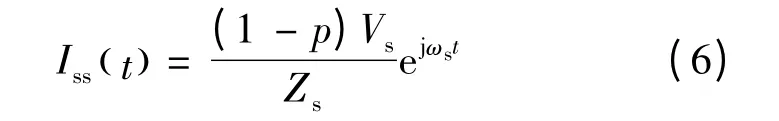
则发电机在静止坐标系下的转子稳态电流:

则双馈机组在三相对称短路故障时投入Crowbar 电路的稳态电磁转矩:

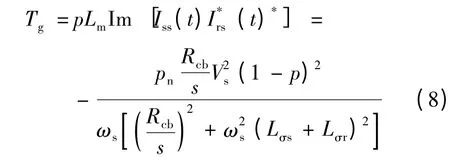
其中，Rcb按标幺值取值，通常在0.2 ～2 之间，双馈机组转差率s 通常在±0.3 以内，定子漏感和转子漏感则通常较小，因此对式(8)作进一步简化后可以得到:

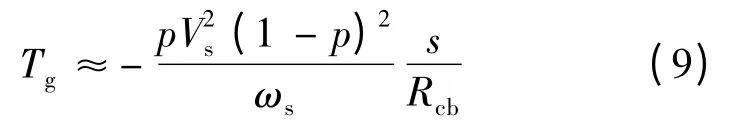
可见，故障期间的稳态电磁转矩主要受电压跌落深度p、机组转差率s 和Crowbar 阻值Rcb影响，而且机组运行在超同步(s ＜0)和次同步(s ＞0)状态下的电磁转矩是反向的。另外从式(9)可以看出，|s|越小(也就是机组转速接近同步速)，p 和Rcb对Tg的影响越小。在超同步速且s 较大而跌落深度p 较小时，选择较小的Rcb可能导致电磁转矩相比故障前增加。

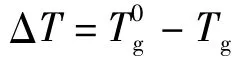
故障发生前发电机电磁转矩的稳态标幺值:

式中:kopt是由风力机决定的一个常数。

由于故障持续短时间内机组转速变化较小，因此可认为式(9)、式(10)中s 基本不变，又p 无法预知且不受人为控制，则ΔT 主要Rcb影响。对于运行在超同步状态的机组，故障发生期间稳态电磁转矩的方向与故障前一致，大小随Rcb的增大而减小，因此较小的Rcb有利于减小故障前后电磁转矩的稳态差值，从而对轴系扭振有利;对于运行在亚同步状态的机组，故障发生期间稳态电磁转矩的方向与故障前反向，大小随Rcb的增大而减小，因此较大的Rcb有利于减小故障前后电磁转矩的稳态差值，从而对轴系扭振有利。

电网不对称故障包括单相对地短路故障、两相对地短路故障和两相相间短路故障，通常采用正负序分离法对不对称故障进行分析。以单相对地短路故障为例，假设A 相发生单相对地短路，跌落深度为p，并假设正序和负序阻抗相等，对故障电压进行正负序分离，有:

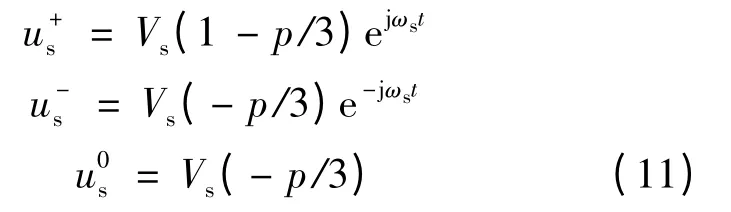
式中:上标+、-、0 分别代表正序、负序和零序分量，对于无中线的双馈发电机不存在零序分量。根据电机理论，电机的稳态磁链强制分量由两部分组成，分别对应于电机电压的正序和负序分量，且两个磁链分量的旋转方向相反。

采用类似的方法，基于图4 等效电路，可以求出定、转子稳态电流的表达式:

则双馈机组在单相短路故障时投入Crowbar 电路的稳态电磁转矩:

根据式(14)可以得出与三相对称故障下类似的结论，同样的分析方法应用于两相对地故障和两相相间短路故障可以得到类似的结论。

由于超同步状态下最严重的情况是电磁转矩减为零，亚同步状态电磁转矩反向对轴系的影响更大，另外根据已有研究结论，较大的Rcb能加快转子电流衰减并减少故障期间机组从电网吸收无功而有利于电网电压恢复，但是增大到一定程度后效果不太显著，且可能致使与功率器件反并联的二极管导通，因此综合考虑可以在适当的范围内选取较大的Rcb值。

2.2 故障恢复后电磁转矩的控制

变流器控制器广泛采用了经典的PI 调节器，电网故障导致转子绕组过流，继而Crowbar 电路投入运行，虽然转子侧变流器的PWM 脉冲被封锁，但是PI 调节器中的积分环节仍在累积误差，导致故障恢复时外环的输出值(也就是内环的给定值)和内环的输出值过大，可能致使SVPWM 模块过调制并导致电流波形畸变，PI 调节器输出值会增加故障恢复时的转矩过冲，给轴系带来负面影响。

一种简单的解决的方法是在检测电网故障时，在故障恢复时刻对PI 调节器的积分值清零，实现方法如图5 所示。

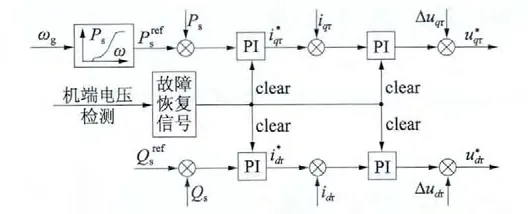
图5 控制系统框图

3 仿真验证

在PSCAD 中建立2 MW 双馈风力发电机组仿真模型，机组的定转子绕组匝数比会很大程度上影响故障期间的暂态特性，考虑严峻情况将定转子匝数比设为1∶ 3。

针对不同Crowbar 阻值以及故障恢复时刻PI调节器积分值清零对轴系扭振的影响进行仿真验证，仿真中传动轴阻尼系数按标幺值取0.5。仿真分两组进行:超同步下发生三相对称故障和次同步下发生单相对地短路故障，电压跌落深度70%(残压30%)，故障持续时间600 ms。其中每组又分为:Rcb=0.1 Ω，无故障恢复积分清零(图中标注“0.1”);Rcb=0.1 Ω，故障恢复积分清零(图中标注“0.1 +清零”);Rcb=0.35 Ω，故障恢复积分清零(图中标注“0.35 +清零”)。仿真结果分别如图6 和图7 所示(结果展示借助MATLAB)。

从图6(a)可以看出，故障发生瞬间，选取较大的Rcb有助于减小电磁转矩的瞬态响应，但是从图6(c)可见，该瞬态响应对扭振的贡献非常有限;对比图6(a)中的“0.1 +清零”、“0.35 +清零”两条曲线可以看出，机组在超同步转速下，较大的Rcb对应于较小的故障期间稳态转矩(电磁转矩以负的数值为正方向)，这与上文分析结果一致，由于Rcb=0.35 Ω 相比于Rcb=0.1Ω 产生了更大的稳态转矩差值，因此其对轴系扭振产生了更大的激发作用(图6(c))，与分析结果一致。对比图6(a)中的“0.1”、“0.1 +清零”两条曲线可以看出，故障恢复时刻积分器清零减小了电磁转矩恢复时的阶跃响应，对于故障恢复后的轴系扭振起到很大的减缓作用(图6(c));从图6(b)可以看出，采用较小的阻值并进行故障恢复积分清零有利于发电机转速稳定。另外，受机电耦合影响，较小的机械振荡对机组输出功率的影响更小，有利于电网电压恢复。

图7 次同步速下发生单相对地故障

从图7(a)可以看出，次同步转速下的双馈机组在Crowbar 投入运行时出现了受Rcb影响的不同程度的转矩反向，对比图7(a)中的“0.1 +清零”、“0.35+清零”两条曲线，Rcb=0.1 Ω 相比于Rcb=0.35 Ω对故障前后稳态转矩差值的影响更大，因此对轴系扭振的影响更大，符合上文的分析结果;对比图7(a)中的“0.1”、“0.1 +清零”曲线，故障恢复时刻积分器清零同样减小了电磁转矩恢复时的阶跃响应，对于故障恢复后的轴系扭振起到很大的减缓作用(图7(c))。

4 结 语

本文对电网故障下双馈机组电磁转矩特性及其对扭振的影响进行了分析，得出了以下结论:

电网故障期间电磁转矩的稳态值对轴系扭振的影响远大于故障发生和故障恢复时刻电磁转矩的暂态响应对轴系扭振的影响。

借助于DFIG 稳态运行等效电路，分析了三相对称故障和以单相对地短路故障为例的不对称故障下Crowbar 阻值选取对故障期间电磁转矩特性的影响。进一步的分析结果表明:Crowbar 阻值选取对轴系扭振的影响与机组运行转速有关，机组运行在亚同步速时，较大的Crowbar 阻值有利于轴系扭振;而当机组运行在超同步速时，较小的Crowbar 阻值有利于轴系扭振抑制。

综合考虑亚同步速转矩反向对扭振影响更大，且较大的阻值能减少故障期间从电网吸收无功，因此建议在合适的范围内选取较大的Crowbar 阻值。故障恢复时PI 调节器积分清零能有效减小电磁转矩过冲，对于轴系扭振能起到很好的改善作用，因此该是强烈建议采用的。

［1］ 张琛，李征，高强，等.双馈风电机组的不同控制策略对轴系振荡的阻尼作用［J］. 中国电机工程学报，2013，33(27):135 -144.

［2］ RIBRANT J，BERTLING L.Survey of failures in wind power systems with focus on swedish wind power plants during 1997 -2005［C］//Power Engineering Society General Meeting，2007.

［3］ MOLINAS M，SUUL J A，UNDELAND T.Extending the life of gear box in wind generatorsby smoothing transient torque with STATCOM［J］. IEEE Transactions on Industrial Electronics，2010，57(2):476 -484.

［4］ 程孟增，张建文，蔡旭，等.电网电压跌落对双馈感应发电机轴系的影响分析［J］.电力系统保护与控制，39(20):17 -23.

［5］ 王勇，张纯江，柴秀慧，等.电网电压跌落情况下双馈风力发电机电磁过渡过程及控制策略［J］. 电工技术学报，2011，26(12):14 -19.

［6］ 郭家虎，张鲁华，蔡旭.双馈风力发电系统在电网三相短路故障下的响应与保护［J］.电力系统保护与控制，2010，38(6):40-48.

［7］ 郑涛 魏占朋，李娟，等.计及撬棒保护的双馈风电机组不对称短路电流特性分析［J］.2014，42(2):8 -14.

［8］ 暴杰，赵慧超，董秀辉，等.电动车用永磁同步电机的三相短路稳态分析与应用［J］.微特电机，2014，42(3):17 -20.

［9］ ANAYA -LARA O，JENKINS N. Wind Energy Generation:Modelling and Control［M］.Germany:John Wiley Sons，2009.