EGM2008重力场模型在铁路GPS高程转换中的应用

李洪杰　梁　永

(铁道第三勘察设计院集团有限公司，天津　300251)

Application of EGM2008 Gravity Field Model in GPS Height Conversion in Railway

LI Hongjie　LIANG yong

EGM2008重力场模型在铁路GPS高程转换中的应用

李洪杰梁永

(铁道第三勘察设计院集团有限公司，天津300251)

Application of EGM2008 Gravity Field Model in GPS Height Conversion in Railway

LI HongjieLIANG yong

摘要基于EGM2008重力场模型分别对平原地区和山区铁路勘测进行GPS高程拟合，并对拟合精度进行分析。

关键词铁路勘测EGM2008重力场模型高程拟合

1概述

地球重力场模型通常是指用来表示地球重力场特征的一些基本参数的组合，是一组球谐系数或引力位系数，是对真实地球重力场的最佳拟合逼近。

EGM2008地球重力场模型为2008年发布的全球超高阶地球重力场模型，该模型的阶次至2159，空间分辨率约为5′×5′，采用GRACE卫星跟踪数据、卫星测高数据和地面重力数据等。

结合具体工程实例，在平原、丘陵、山区不同地形条件下，对EGM2008重力场模型进行GPS高程转换，并对其精度进行分析。

2GPS高程转换方法

GPS高程转换基本原理是：利用GPS定位技术测得所求测点的大地高HA，通过地球重力场模型求得测点的高程异常值ζA，然后利用大地高、正常高与高程异常的基本关系求得测点的正常高hA

(1)

式中：hA、HA和ζA分别为A点的正常高、大地高和高程异常。

目前常用的GPS高程转换方法有三种。

(1)高精度、高分辨率的似大地水准面模型高程转换：高精度似大地水准面模型的确定是一个比较复杂的问题，涉及地球重力场模型、地面重力测量、GPS/水准测量以及高分辨率的数字地形模型等方面内容，实际应用中需要将地面点坐标统一到似大地水准面模型对应的基准。

(2)通过地球重力场模型GPS高程转换：该方法需要将地面点GPS坐标基准统一到所采用的地球重力场模型基准，其精度主要受所采用的地球重力场模型的精度和分辨率、大地高精度，以及所采用地球重力场模型所表示的全球似大地水准面和我国高程基准面之间系统偏差的综合影响，直接转换时存在系统性偏差。

(3)GPS/水准点高程转换：通过联测一定数量的GPS/水准点，利用直线、二次曲线、平面、曲面以及多面函数等高程拟合的方法，该方法的本质是利用若干个已知GPS水准点或水准高差观测值，通过拟合方法将GPS测量得到的大地高转换为正常高，其拟合高程的精度和可靠性过多地依赖已知GPS/水准点的密度、分布状况以及测区地形起伏情况等，适合于小范围的高程转换。

本文中的GPS高程转换的方法是综合方法2和方法3，首先利用地球重力场模型计算得到GPS点的模型高程异常，由于全球重力场模型计算的高程异常与我国85高程基准存在系统性差异，因此还需要利用GPS/水准点进行模型残差纠正，得到最终的高程异常值，然后利用式(1)求得测点正常高。

首先利用地球重力场模型计算得到GPS点的模型高程异常，地球表面上任意点A的模型高程异常可由下式得到

(2)

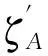
(3)

算出GPS网中所有进行了常规水准联测点上的大地水准面模型高程异常残差值，采用直线、曲线、平面、曲面以及多面函数等内插方法拟合出GPS网未进行过常规水准联测点上的大地水准模型高程异常残差值Δζi，并利用这些值对这些点上由大地水准面模型所计算出的高程异常值ζGM进行改正，最后得到经过改正后的高程异常值ζi=ζGM+Δζi。

3重力场模型高程转换精度分析

3.1　平原地区GPS网高程拟合精度分析

哈尔滨至齐齐哈尔城际铁路：地势较平坦，线路里程约300 km，采用天宝GPS接收机进行三等GPS静测量，边连接方式构网，然后对观测数据进行基线解算预处理，再对选取均匀分布的4个水准点、6个水准点、12个水准点分别进行高程拟合，与二等水准高程进行比较，对内符合和外符合精度分别进行统计。

(1)选取均匀分布的4个已知水准点(平均点间距70 km)进行高程拟合，拟合方式为平面拟合，首先对其内符合精度进行统计，拟合残差最大值-13.3 mm，最小值为3.7 mm。

外符合精度统计：对沿线58个水准点进行高程拟合，与已知二等水准高程进行比较，其残差如图1所示。

图1　4个已知点高程拟合残差曲线

与已知水准点的高程进行比较：较差最大值为-56.5 mm，最小值为1.9 mm，较差中误差为±21.7 mm。

(2)选取均匀分布的6个已知水准点(平均点间距50 km)进行高程拟合，拟合方式为平面拟合，首先对其内符合精度进行统计，拟合残差最大值-17.9 mm，最小值为0.0 mm。

外符合精度统计：对沿线58个水准点进行高程拟合，与二等水准高程进行比较，其残差如图2所示。

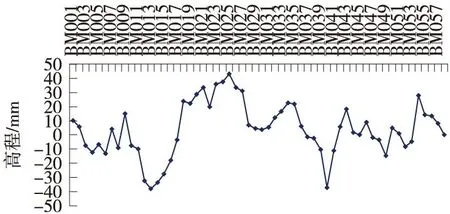
图2　6个已知点高程拟合残差曲线

与已知水准点的高程进行比较：较差最大值为43.1 mm，最小值为0.0 mm，较差中误差为±19.2 mm。

(3)选取均匀分布的12个已知水准点(平均点间距25 km)进行高程拟合，首先对其内符合精度进行统计，拟合残差最大值-20.9 mm，最小值为-2.7 mm。

外符合精度统计：对沿线58个水准点进行高程拟合，与二等水准高程进行比较，其残差如图3所示。

图3　12个已知点高程拟合残差曲线

与已知水准点的高程进行比较：较差最大值为-43.1 mm，最小值为0.4 mm，较差中误差为±18.1 mm。

3.2　山区GPS网高程拟合精度分析

长沙至昆明铁路位于山区，植被茂密，线路里程约400 km，采用天宝GPS接收机进行三等GPS静态测量，边连接方式构网。首先进行内业数据处理，再进行高程拟合，对均匀分布的6个水准点、9个水准点进行高程拟合，然后与二等水准高程进行比较，对其内符合和外符合精度分别进行统计。

(1)选取均匀分布的9个已知水准点(平均点间距50 km)进行高程拟合，拟合方式为曲面拟合，对其内符合精度进行统计，拟合残差最大值41.9 mm，最小值为4.6 mm。

外符合精度统计：对沿线158个水准点进行高程拟合，与二等水准高程进行比较，其残差如图4所示。

图4　9个已知点高程拟合残差曲线

与已知水准点的高程进行比较：较差最大值为-89.6 mm，最小值为-0.5 mm，较差中误差为±22.0 mm。

(2)选取均匀分布的5个已知水准点(平均点间距15 km)，对上述BM77～BM106高程差异较大的段落进行单独高程拟合，对其内符合精度进行统计，拟合残差最大值-22.6 mm，最小值为-4.9 mm。

外符合精度统计：对沿线27个水准点进行高程拟合，与二等水准高程进行比较，其残差如图5所示。

图5　5个已知点高程拟合残差曲线

与已知水准点的高程进行比较：较差最大值为-56.3 mm，最小值为2.7 mm，较差中误差为±10.5 mm。

4结论

(1)平原地区GPS网高程拟合精度要比山区拟合精度高。以已知水准点点间距在50 km左右时为例，平原地区GPS高程拟合误差在±45 mm之间，中误差为±19.2 mm；而山区GPS高程拟合误差在±90 mm之间，中误差为±22.0 mm。

(2)拟合精度与已知水准点的点间距相关，点间距越小，其高程拟合精度越高。

(3)采用点间距50 km和25 km两种方法进行拟合，其高程结果差异不大。因此，在平原地区采用GPS进行高程拟合时，GPS联测已知点可以适当稀疏。

(4)由于山区的高程异常变化剧烈，而重力场模型分辨率相对比较低，其拟合高程误差大，在山区采用GPS进行高程拟合时，GPS联测已知点需加密，同时宜分区拟合计算。

参考文献

[1]李建成，陈俊勇，宁津生，等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉：武汉大学出版社，2003

[2]张兴福，刘成，王国辉，等.基于EGM2008重力场模型的GPS高程转换方法及精度分析[J].地球物理学进展，2012，27(1)

[3]王春宝.基于EIGEN-CG01C地球重力场模型的GPS高程转换方法研究[J].铁道勘察，2007，33(4)

[4]章传银，郭春喜，陈俊勇，等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报，2009，38(4)：283-289

[5]孔祥元，郭标明，刘宗泉. 大地测量学基础.[M]武汉：武汉大学出版社，2001．

[6]刘成，张幸福.EGM2008重力场模型在GPS高程拟合中的应用分析[J].铁道勘察，2009，35(1)

[7]侯俊岭.高精度地球重力场模型用于GPS高程转换[J].铁道勘察，2010，36(6)

[8]宁津生，罗志才，李建成.我国省市级大地水准面的现状及技术模式[J].大地测量与地球动力学，2004，24(1)：4-8

[9]郭海荣，焦文海，杨元喜.1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J].测绘学报，2004,3(2)：100-104

中图分类号：P223+.0；P226+.3

文献标识码：B

文章编号：1672-7479(2015)03-0003-03

作者简介：第一李洪杰(1970— )，男，毕业于北京交通大学，工程师。

收稿日期：2015-03-05