空间相机摆扫成像建模及摆镜角速度残差分析
苗壮 何斌 王俊琦 陈起行 杨小杰
(1 中国科学院长春光学精密机械与物理研究所,长春 130033)
(2 中国科学院大学,北京 100049)
(3 吉林大学,长春 130022)
0 引言
TDICCD空间相机推扫成像技术现已日趋成熟,且可以满足大多数的技术指标。随着大视场成像指标的提出,在可见光相机、近红外和短波红外空间相机中都采用推扫成像的方式,并取得了良好的实际应用效果。但是对于海洋军事目标监视应用的长波红外相机,由于受限于光学口径尺寸以及 CCD器件约束,目前还只能应用有限的CCD拼接[1-2],采用摆扫成像方式可以在保证其它技术指标的前提下,实现大视场的要求。但是摆扫成像过程中卫星平台的轨道运动、姿态变化、摆扫反射镜的摆动以及地球自转运动等,形成相机像面的像移,为了保持空间相机像面与地物相对静止,需要进行像移匹配。目前,国外比较先进的扫描成像机构有:美国的 ETM+、MODIS,日本的GLI、WISE,法国的 SPOT-5上的HRG等,摆镜作为扫描成像的关键技术,其资料保密甚严,可查阅资料少之又少[3-4];国内方面,相关资料也相对较少,文献[5]提出的摆扫成像模型是针对整机的横滚机动进行摆扫,相对于针对摆镜的摆扫,控制起来更加的复杂与困难。为此建立一种摆扫像移匹配数学模型来补偿相机像面各点处的像移,同时针对摆镜角度的波动进行残差分析。
1 摆扫成像的视场特点
推扫式成像系统的视场与地面像元分辨率[6](ground sample distance,GSD)以及有效像元数Nc有关,一旦GSD和Nc确定之后,其视场大小也随之确定,如图1(a)所示。而摆扫成像方式之所以能满足大视场的指标,在于其摆镜的工作方式,如图1(b)所示[7],扫描系统通过摆镜的转动来改变光轴的指向以实现大视场的扫描成像。经比较可以看出,在相同的地面像元分辨率和有效像元数的情况下,摆扫成像方式的视场可以随着摆镜转角的增加而增加,而推扫式成像系统的视场则为定值。
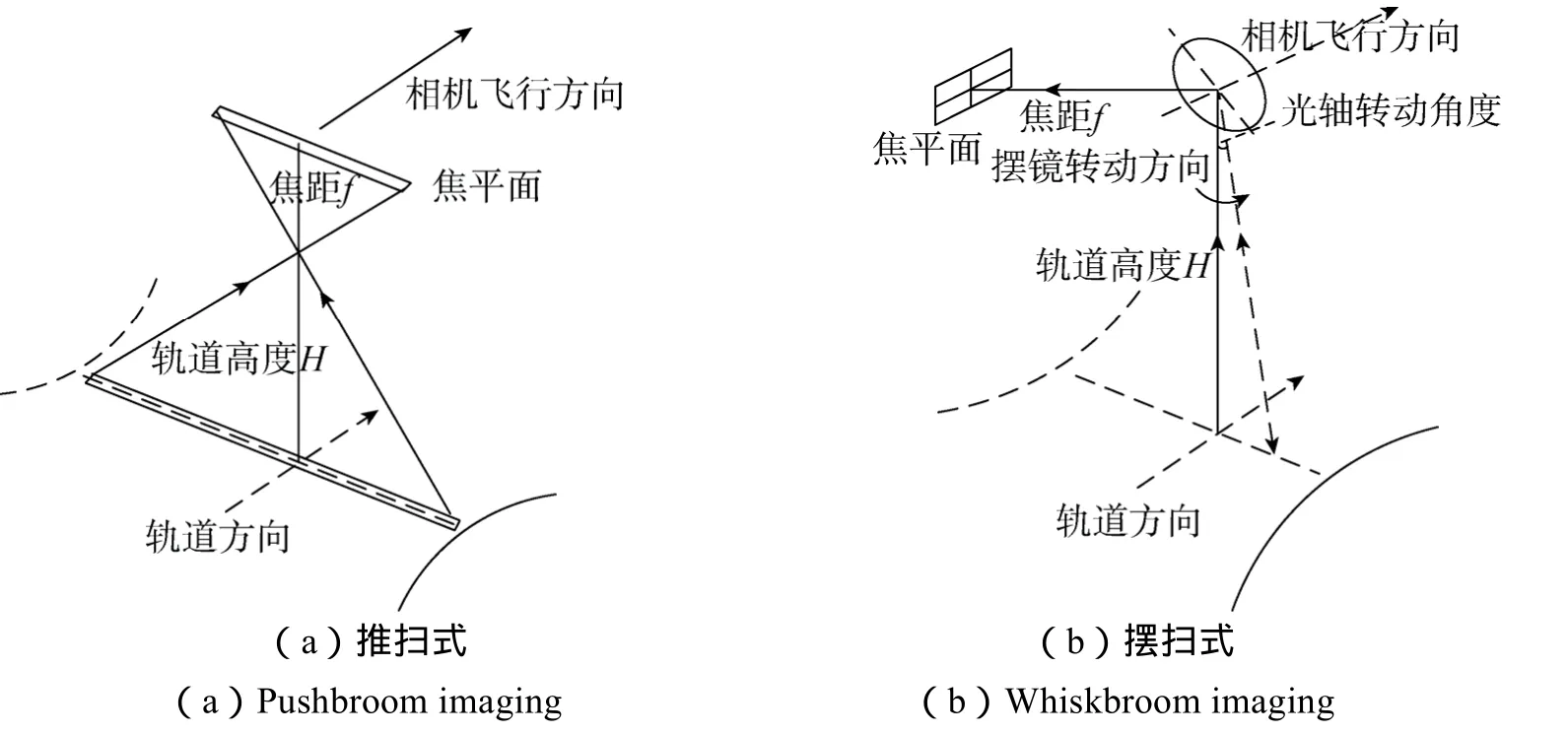
图1 推扫式和摆扫式成像方式示意图Fig.1 Schematic of pushbroom imaging and whiskbroom imaging
2 摆扫成像坐标系的定义
从地面景物到像面的过程中,共涉及到9个坐标系,各坐标系定义如下(全部采用右手坐标系)[8-10]:
景物地理坐标系G(G1,G2,G3):G系原点为光轴指向的地面景物点;G3轴的指向,为光轴指向相机方向;G1轴与卫星轨道前进方向相同,G1,G2,G3构成右手坐标系。
视轴景物地心坐标系K(K1,K2,K3):原点与地心重合。K3轴指向相机光轴指向的景物点;K1轴与过K3轴垂直于轨道面的平面相垂直,指向卫星轨道前进方向;K1,K2,K3构成右手坐标系。
地心惯性坐标系I(I1,I2,I3):原点与地心重合。I2轴指向地球北极;I3轴指向卫星的轨道平面与赤道的降交点;I1,I2,I3构成右手坐标系。
地球坐标系E(E1,E2,E3):坐标系固连于地球,原点与I系的原点重合,E2指向北极,地球坐标系E在I系内逆时针方向以角速度ω绕E2轴转动。
卫星轨道坐标系B(B1,B2,B3):原点在轨道上。B1轴指向轨道切向;B3轴指向天顶;B2与轨道面垂直。
卫星坐标系S(S1,S2,S3):该坐标系原点与轨道坐标系原点重合,卫星无姿态时两个坐标系重合,卫星的三轴姿态φ,θ,ψ是指S系在B系中的三轴姿态,欧拉姿态角转序为1-2-3。
摆镜坐标系M(M1,M2,M3):初始时刻,卫星坐标系绕着S1旋转45°即为摆镜初始坐标系;摆镜扫描时,摆镜坐标系绕着M1以角速度ωx进行摆动。
相机坐标系C(C1,C2,C3):相机物镜的主点为该坐标系的原点,当相机在卫星内无安装误差或者很小时,相机与卫星坐标系可以认为是重合的。
像面坐标系P(P1,P2,P3):坐标系原点在像面中心,C系沿C2轴平移f,P1、P3与C1、C3反向后即得到P系,P1,P3组成像面。
各坐标系之间的转换关系如图2所示(图中的灰色部分由上到下的标注表示的是由前一个坐标系到后一个坐标系的转换关系和顺序):
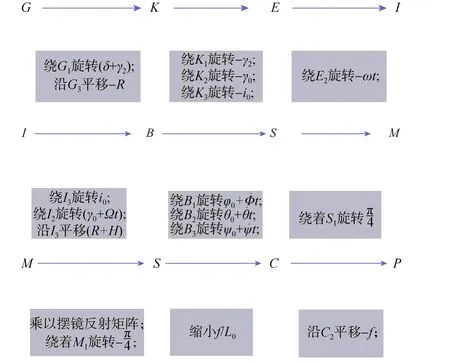
图2 各个坐标系之间的变换Fig.2 Transformation between various coordinate systems
摆扫成像过程,景物经过光学系统,最后经过扫描变换矩阵进入扫描镜动坐标系,由反射矩阵进行反射,再由扫描变换矩阵的逆矩阵转换到静坐标系中,获得出射矢量[11]。由摆扫成像各坐标系的变换关系和摆镜坐标系的定义可知,摆镜旋转矩阵

所以地面上某点地理位置对应的像面坐标表达式如下:
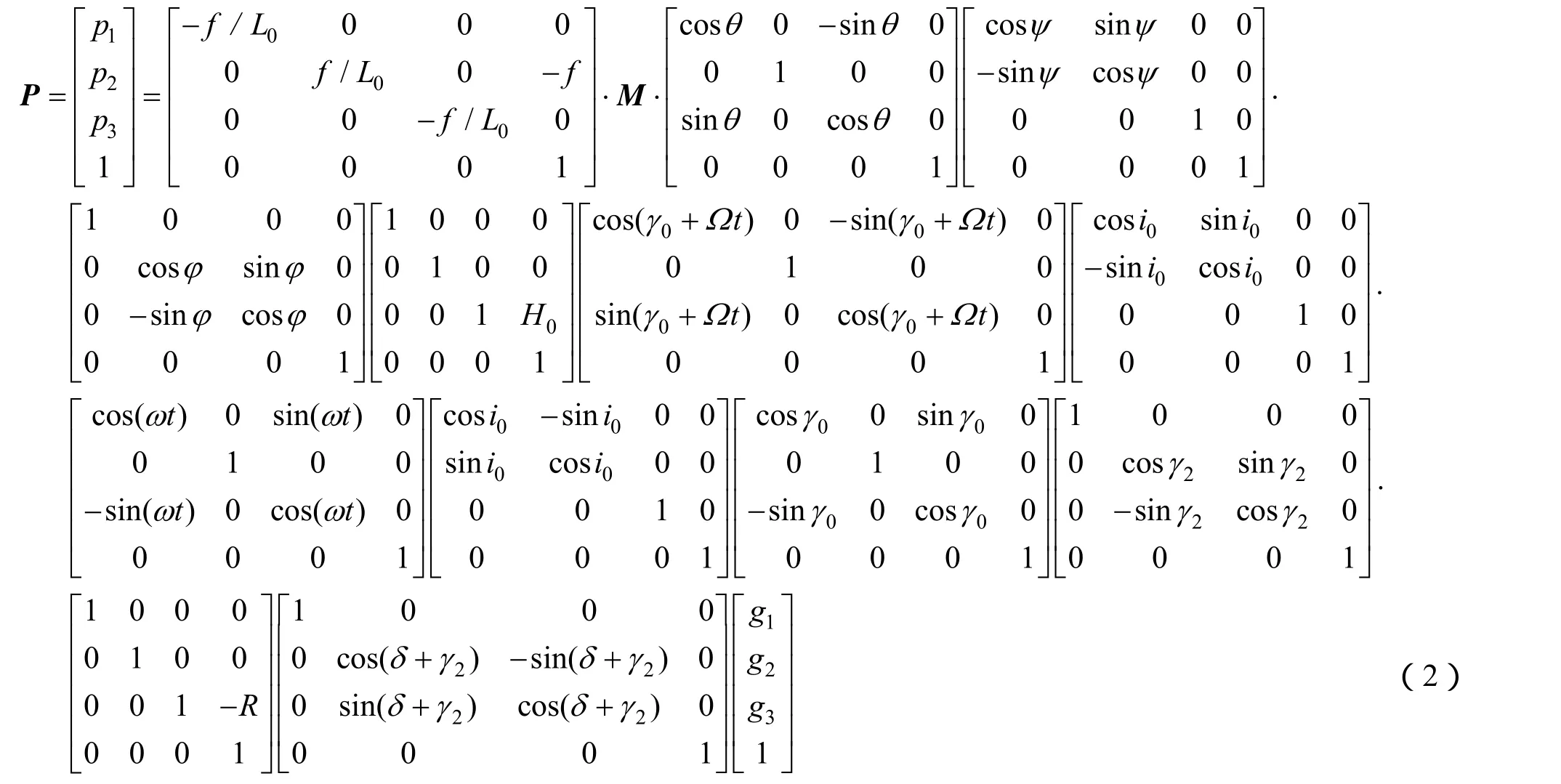
式中

将式(2)两边对时间t微分后,令t=0,即可求得像面上像点P对应的像移方程



3 试验仿真
由像移速度表达式,对其中所用到的参量进行误差分配,并用蒙特卡洛法[12]进行误差合成,最终估计像移速度误差。本文中相机探测器选择三片 96×4 096的 TDICCD拼接而成,探测器的像元尺寸为8.75μm,轨道高度为1 200km。为保证摆扫过程地面成像不漏扫,可以设定摆镜的转动速度ωx=0.6(°)/s,经过计算知,当ωx=0.6(°)/s时,其对飞行器的反向动量角速度仅为0.000 1(°)/s,不及横滚角速度的1/10。根据平台总体设计指标(由像移残差造成的MTF下降不超过5%时),即满足96级TDICCD相机对地成像品质要求,其中的17个变量误差分配如下[13]:
姿态控制精度δφ=δθ=δψ=0.03°;
摆镜角速度控制精度δωx=0.001(°)/s;
姿态测量精度σφ=σθ=σψ=0.001°;
卫星轨道速度允许误差:σvs=0.01km/s;
卫星轨道高度允许误差:σH=0.15km;
星下点纬度允许误差:σλk=0.027°;
光学系统焦距相对允许误差:σf=0.05%。
已知由控制精度产生的误差服从均匀分布,其它的误差服从正态分布,因此以上各参数的分布矩阵如表1所示:
1)如表1,对应公式中的11个随机变量和6个姿态初始值产生的17个伪随机数序列。17个随机变量中,φ0、θ0、ψ0、φ⋅、θ⋅、ψ⋅为均匀分布,因此产生均匀分布矩阵。而其余11个变量为正态分布,因此产生归一化的正态分布矩阵。
2)将i=1时的φ0(i=1)、θ0(i=1)、ψ0(i=1)、φ⋅0(i=1)、θ⋅0(i=1)、ψ⋅0(i=1)的值,以及其它的常量参数带入式(5)和式(6),可以获得i=1时,即第一个采样点VP(i=1)和β(i=1)。
3)将 i=1时的 φ0(i=1)+△φ(i=1)、θ0(i=1)+△θ(i=1)、ψ0(i=1)+△ψ(i=1)、)、的值,以及其它的常量参数带入式(5)和式(6),可以获得ti=1时刻(VP+△VP)(i=1)和(β+△β)i=1的值。由此可得
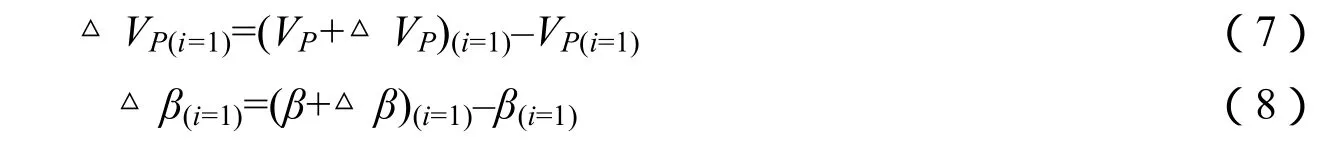
4)将γ0增加一个增量,即增加航天器轨道运动的纬度幅角γ0(i=2),并选取i=2时随机变量及其它常量带入到式(7)和式(8),得到△VP(i=2)和△β(i=2)。
5)重复以上步骤,最终得到△VP和△β合成误差的数列。重复(1)~(5)将其带入到摆扫成像模型公式,得到摆扫成像模式下的偏流角、像移速度及其残差等。其仿真数据如图3~5所示。

表1 参数误差分布矩阵表Tab.1 Matrix of parameters error distribution

图3 摆扫成像模型1 000次统计试验中不同偏流角次数Fig.3 Number of different drift angle of whiskbroom imaging model in 1 000 statistical experiments
图3表明,摆扫式成像过程中,在TDICCD进行像移匹配时,与推扫式成像方式不同,需要将偏流角调整机构旋转 83°,即其 TDICCD的积分方向在垂直轨道方向上有所偏离,进而实现像移速度与TDICCD电荷转移速度在同一方向,由此可知其对地面景物所成的像如图4所示。图4中,摆扫相机扫描的地面轨迹是空间相机飞行,摆镜运动和地球自转合成运动的结果。其中的阴影部分是两次扫描过程中的重叠部分。
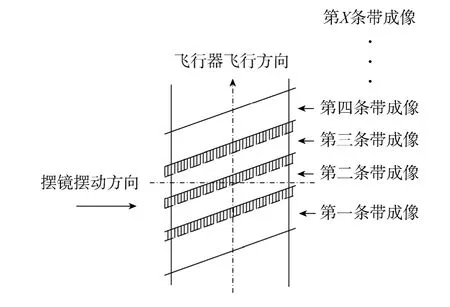
图4 摆扫成像扫描地面图形(单摆)Fig.4 Ground graphic of whiskbroom scan(one side)

图5 摆扫成像模型1 000次统计试验中不同像移残差次数Fig.5 Number of different image motion velocity error of whiskbroom imaging model in 1 000 statistical experiments
由图5可知,在摆镜角速度误差△ωx=0.001(°)/s时,其产生的像移角速度误差△VP最大值为0.7mm/s,这在TDICCD电荷转移的过程中是需要考虑的,如果像移速度残差过大,在曝光时间过大或积分级数过高时会使图像的品质严重下降,而造成图像模糊。所以特对因不同摆镜角速度误差而造成的像移速度残差进行了MTF仿真验证,其MTF如图6所示。
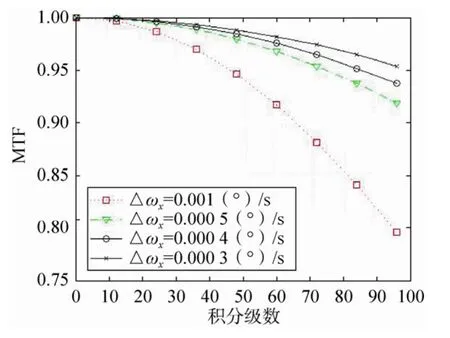
图6 不同积分级数下的MTFFig.6 MTF in different integral series
4 结束语
TDICCD空间相机摆扫成像像移速度模型在齐次坐标变换的基础上,通过矩阵分析法加以摆扫反射镜矩阵而构成。采用蒙特卡洛的方法,对摆扫成像方式的随机变量波动进行误差合成。相比推扫成像模型而言,摆扫成像方式的参量误差更多,故其像移速度残差也较大。同时分析了在不同积分级数下的MTF,发现当摆镜角速度误差分别为△ωx=0.001(°)/s,△ωx=0.000 5(°)/s,△ωx=0.000 4(°)/s时,只有在积分级数N分别小于48,72,84时才能够满足MTF≥0.95;当△ωx=0.000 3(°)/s,随着积分级数的增加,MTF的下降十分平缓,当 M=96时,MTF>0.95。该结果表明该摆扫成像像移模型在摆镜角速度ωx=0.6(°)/s,摆镜角速度误差△ωx=0.000 3(°)/s时,对成像品质基本无影响。目前的技术水平所能到达的是控制精度为0.000 5(°)/s,当积分级数N≤72时,可以保证MTF≥0.95,即对图像品质无影响。仿真结果与理论分析相符合,对工程应用有一定的指导意义。
(
)
[1] 杨秉新. TDICCD相机的相对孔径与器件像元尺寸关系的研究[J]. 航天返回与遥感, 2001, 22(2): 9-12. YANG Bingxin. Investigation on the Relationship of Relative Aperture to Pixel Dimensions for TDICCD Camera[J]. Spacecraft Recovery & Remote Sensing, 2001, 22(2): 9-12. (in Chiness)
[2] 杨桦, 郭悦, 伏瑞敏. TDICCD的视场拼接[J]. 光学技术, 2003, 29(2): 226-228. YANG Hua, GUO Yue, FU Ruimin. Study on Field Butting of TDICCD[J]. Optical Technique, 2003, 29(2): 226-228. (in Chinese)
[3] 芮涛. 大口径长焦距扫描成像光学系统像质研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. RUI Tao. The Imaging Quality Research on Large Aperture and Long Focal Length Scanning Optical System[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese)
[4] 张媛. 星载TDICCD相机侧摆成像像移速度建模与分析[D]. 哈尔滨: 哈尔滨工业大学, 2013. ZHANG Yuan. Modeling and Analysis of Image Motion Velocity for Satellite Borne TDICCD Camera in Roll Attitude[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese)
[5] 杨飞, 金光, 曲宏松. 航天时间延迟积分 CCD相机摆扫成像快速几何校正设计与分析[J]. 光学学报, 2014, 34(1): 0111001-1-0111001-7. (in Chinese)YANG Fei, JIN Guang, QU Hongsong. Design and Analysis about Rapid Geometric Correction of Space Whiskbroom Time Delayed and Integeration CCD Camera[J]. Acta Optica Sinica, 2014, 34(1): 0111001-1-0111001-7. (in Chinese)
[6] 周峰, 乌崇德. 提高航天传输型CCD相机地面像元分辨率方法研究[J]. 航天返回与遥感, 2002, 23(3): 35-42. ZHOU Feng, WU Chongde. A Method for Improving GSD of Space Real-time Transmission CCD Camera[J]. Spacecraft Recovery & Remote Sensing, 2002, 23(3): 35-42. (in Chinese)
[7] James C S. Landsat7 on-orbit Modulation Transfer Function Estimation[J]. SPIE, 2001, (4540): 50-61.
[8] 王家骐, 于平, 颜昌翔. 航天光学遥感器像移速度矢计算数学模型[J]. 光学学报, 2004, 24(12): 1585-1589. WANG Jiaqi, YU Ping, YAN Changxiang. Space Optical Remote Sensor Image Motion Velocity Vector Computational Modeling[J]. Acta Optica Sinica. 2004, 24(12): 1585-1589. (in Chinese)
[9] 王运, 颜昌翔. 基于差分法的空间像移速度矢量计算[J]. 光学精密工程, 2011, 19(5): 1054-1060. WANG Yun, YAN Changxiang. Computation of Image Motion Velocity Vector for Space Camera based on Difference Method[J]. Optics Precision Engineering, 2011, 19(5): 1054-1060. (in Chinese)
[10] 颜昌翔, 王家骐. 航相机像移补偿计算的坐标变换方法[J]. 光学精密工程, 2000, 8(3): 203-207. YAN Changxiang, WANG Jiaqi. The Method of Coordinate Transformation for Image Motion Compensation Calculation of Aerial Carema[J]. Optics Precision Engineering, 2000, 8(3): 203-207. (in Chinese)
[11] 陈世平. 空间相机设计与试验[M]. 北京: 中国宇航出版社, 2009: 186-187. CHEN Shiping. Space Camera Design and Experiment[M]. Beijing: China astronautics Press, 2009:186-187. (in Chinese)
[12] 朱本仁. 蒙特卡洛方法引论[M]. 济南: 山东大学出版社, 1985: 5-11. ZHU Benren. Introduction to Monte Carlo Method [M]. Jinan: Shandong University Press, 1985: 5-11. (in Chinese)
[13] 闫得杰, 徐抒岩, 韩诚山. 飞行器姿态对空间相机像移补偿的影响[J]. 光学精密工程, 2008, 16(110): 2199-2203. YAN Dejie, XU Shuyan, HAN Chengshan. Effect of Aerocraft Attitude on Image Motion Compensation of Space Carema[J]. Optics Precision Engineering, 2008, 16(110): 2199-2203. (in Chinese)
[14] 马天波, 郭永飞, 李云飞. 科学级TDICCD相机的行频精度[J]. 光学精密工程, 2010, 18(9): 2028-2035. MA Tianbo, GUO Yongfei, LI Yunfei. Precision of Row Frequency of Scientific Grade TDICCD Camera[J]. Optics Precision Engineering, 2010, 18(9): 2028-2035. (in Chinese)
[15] 庄绪霞, 王治乐, 阮宁娟, 等. 像移对星载 TDICCD相机成像品质的影响分析[J]. 航天返回与遥感, 2013, 34(6): 66-73. ZHUANG Xuxia, WANGZhile, RUAN Ningjuan, et al. Influence Analysis of Image Motion on Image Quality of Satellite-board TDICCD Camera Optical System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 66-73. (in Chinese)

