松耦合旋转变压器电感的参数化分析与设计
吴聪苗,皮 钧,林坤艺
(集美大学机械与能源工程学院,福建 厦门 361021)
松耦合旋转变压器电感的参数化分析与设计
吴聪苗,皮钧,林坤艺
(集美大学机械与能源工程学院,福建 厦门 361021)
[摘要]由于松耦合旋转变压器存在较大气隙,其电感量难以计算,为了省去计算机建模和仿真的步骤,缩短设计时间,针对壶型磁芯和邻近型线圈组成的松耦合旋转变压器建立磁阻模型,根据其大气隙的特点,采用磁阻分析的方法得到其等效电路模型.再以磁芯和线圈的尺寸为参数,分析、推导得出松耦合旋转变压器励磁电感和漏感的计算公式,并根据设计参数间的关联,给出了一个设计流程图.最后通过计算、仿真和实验三者对比分析,验证了励磁电感和漏电感公式的正确性.
[关键词]松耦合;旋转变压器;气隙;漏感
0引言
基于电磁感应耦合理论的无接触能量传输(contact-less transfer of energy,CTE)技术摆脱了传统物理连接的束缚,实现了供电线路和用电设备之间的物理分离及能量传输,这种形式增加了取电的灵活性,可以广泛地运用于工业、民用、国防及医疗等各个领域.目前,CTE技术正朝着大功率设备的无接触供电,小功率便携设备的无接触充电,特殊工况下电气设备的无接触供电等方向发展[1-3].
在旋转工况下,通常使用碳刷和滑环结构传递电能.碳刷和滑环结构存在导线裸露、电弧、接触火花、滑动磨损、积碳等缺陷,而松耦合旋转变压器(以下简称松耦合变压器)没有裸露的电线,没有机械摩擦和磨损,可少维护甚至免维护,拥有长久的使用年限.采用无接触能量传输方式的松耦合变压器代替原有的碳刷和滑环结构提高了用电的可靠性和安全性,是一种在旋转工况下较为理想的解决方案.国内已有学者提出将松耦合变压器应用于铣床上实现旋转超声加工[4],国外学者已将该技术运用于机器人的关节、卫星的太阳能电池板、机载雷达等关键部位[5-6].由于松耦合变压器存在较大气隙,传统紧耦合变压器的设计方法不再适用,一般通过软件仿真得出其励磁电感和漏感.为省去计算机建模和仿真的步骤,本文以磁芯和线圈的结构尺寸为参数,量化了励磁电感和漏感,以使设计计算更加便捷,同时根据设计过程中各参数变量之间的关联,设计了流程图.
1松耦合变压器的建模分析
壶型磁芯上下分离且形状尺寸相同,可以更为方便的使用磁芯窗口,在磁耦合和传导损耗方面有更好的表现,而且市面有多种型号的壶型磁芯(pot core)可供使用,具有良好的经济性.邻近型线圈两个线圈分别放置于两个磁芯凹槽内,结构简单且具有更好的窗口利用率[7].故本文选取拥有壶型磁芯和邻近型线圈的松耦合变压器进行分析.
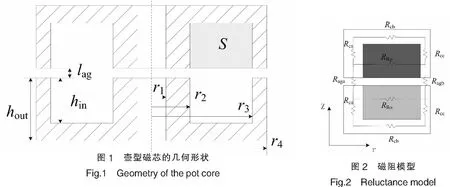
图1为壶型磁芯截面几何形状及其参数.图1中r1、r2、r3、r4分别为磁芯各部分的半径,hin为窗口高度,hout为磁芯整体高度,lag为气隙长度,S为窗口面积.
1.1 磁模型分析
根据不同的磁芯几何形状和线圈的布局,将会产生不同的磁通分布,松耦合变压器的固有气隙使漏感大大增加.根据松耦合变压器的结构特点和磁路运行特点建立如图2所示的磁阻模型[8-9].
某磁路j上的磁阻可以表示为Rj=lj/(μ0μrAj).其中:Rj为磁阻;lj为磁路长度;μ0为真空磁导率;μr为材料的相对磁导率;Aj为磁路横截面积.分别代入磁芯几何尺寸可得磁芯各部分的磁阻[10]
Rca=Rcc=Δz/(μ0μrπ(ro2-ri2));Rcb=ln(ro/ri)/(2πμ0μrz).其中:ro为该部分磁芯外径;ri为该部分磁芯内径;z为高度.
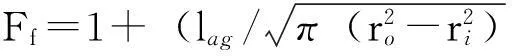
电感L与线圈匝数N的平方成正比,与磁阻R成反比,即L=N2/R.
磁芯截面几何形状与空气隙合成一个闭合的磁通环路,通常上下磁芯形状、尺寸相同,得励磁电感
(1)
其中:Np为初级线圈匝数.
在松耦合变压器中,由于初、次级磁芯分离,漏感较大,不能忽略,且漏感没有固定集中的磁路,不能通过磁路模型分析计算得到.初级线圈漏感的能量并没有通过电磁感应传递到次级,而是储存在线圈及线圈之间的气隙中,所以该体积内的磁场能量即为漏感的能量[9],即LlkI2/2=(∫vB·Hdv)/2.其中:Llk为漏感;I为电流;B为磁通密度;H为磁场强度;v为线圈和线圈之间空气隙的总体积.
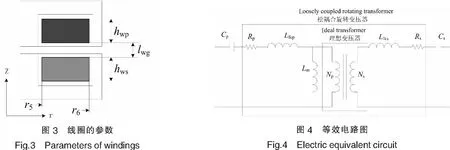
漏感与线圈的形状、位置有非常重要的关系.图3为线圈的形状和位置参数,r5、r6分别为线圈相对于轴线的内径和外径,hwp、hws分别为初、次级线圈的轴向高度,lwg为初、次级线圈之间的距离.
线圈中的磁场强度是其轴向高度的函数[9],即H(z)=(Npip/(r6-r5))(z/hwp).线圈之间的气隙的磁场强度近似于H=Npip/(r6-r5).
假设Npip=Nsis,则总的漏感为
(2)
该漏感值是以初级线圈的角度出发计算得到的,初级线圈的漏感应为该漏感值的一半.同理可得次级线圈的漏感[12].
1.2 电模型分析
通过分析松耦合变压器的磁阻模型,得到如图4所示的等效电路模型.其中:Cp、Cs为补偿电容;Lm为励磁电感;Llkp和Llks分别为初、次级漏感;Rp和Rs分别为初、次级等效电阻.大虚线框内为松耦合变压器的等效电路,小虚线框内可视为理想变压器.松耦合变压器存在较大的漏感,消耗大量的无功功率,为了提高功率传输能力和能源的利用率,一般采用串联或者并联电容的方法补偿松耦合变压器的漏感,提高有功功率[13-14].
线圈等效电阻的大小决定了传导损耗,将会严重影响松耦合变压器的效率,松耦合变压器的工作频率一般较高,此时线圈的等效电阻受趋肤效应和邻近效应的影响较大,不能忽略,因此计算也变得复杂.文献[15]给出了变压器多层线圈在任意电流波形下的交流电阻的计算公式.
在松耦合变压器的初级线圈中存在一个额外的励磁电流,该电流独立于负载状况,并未对负载做功,其效果是增加了传导损耗,其峰值为[16]
(3)
其中:Vin为初级输入电压;D为占空比;Tsw为功率开关管的开关周期.
初级线圈的电流是励磁电流与反映负载电流之和
(4)
其中:Ip为初级电流;Is为次级电流;Ns为次级线圈匝数.
2松耦合变压器的设计
由于松耦合变压器初、次级磁芯分离,磁路通过气隙完成闭合,因此,其磁路和电路上区别于传统紧耦合变压器.根据安培环路定律,松耦合变压器的磁路经过两次气隙,一般认为气隙磁通和磁芯磁通相等,则
(5)
其中:B为平均磁通密度;lc为磁芯磁路的长度.式(5)可用于计算和验证松耦合变压器的磁通密度是否满足设计要求.磁芯磁路长度lc虽然占总磁路的绝大部分,但是由于一般选择的磁芯材料相对磁导率μr较高,所以该部分几乎可以忽略不计,磁通密度主要受气隙长度影响.
在设计之初,应尽可能减小气隙长度,以提高耦合程度和传输效率.式(1)中,磁阻主要集中在Raga和Ragb,这也是由于空气磁导率低的缘故.由于气隙的存在,松耦合变压器的励磁电感比相同情况下的紧耦合变压器小1-2个数量级,磁通密度也小的多,所以在传输相同功率的情况下,松耦合变压器比紧耦合变压器体积大得多.
在初步选定磁芯型号或者暂定磁芯几何尺寸时,以P=πJSkffBmaxAe作为参考,其中:P为功率;J为电流密度;S为窗口面积;k为窗口填充系数;Bmax为最大磁通密度;Ae为磁芯的有效截面积.
在松耦合变压器中,漏感的存在将会引起压降.从式(2)可以看出漏感与线圈的形状、位置关系密切,在气隙长度已经确定的情况下,调整磁芯几何参数和线圈的位置可以有效地减小漏感.在保证窗口面积的情况下,减小hwp、hws和r5,相当于将壶形磁芯和线圈做得扁而宽,可以有效地减小漏感,从而将更多的能量传递到次级.
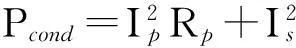
松耦合变压器一般工作在高频状态下,除了传导损耗,磁芯损耗也不容忽视,有时甚至高于传导损耗.磁芯损耗可由Steinmetz方程Pcore=Cm·C(T)·fα·Bβ·Vcore计算.
其中:Cm、α、β为磁芯材料系数;C(T)为温度系数;Vcore为磁芯体积.则松耦合变压器总损耗为P∑=Pcond+Pcore.
这些损耗作用于线圈和磁芯上,致使松耦合变压器发热产生温升.温升对松耦合变压器有重要意义,因为磁性材料对温度较为敏感,许多参数随温度变化而变化,因此设计时应该将温升控制在一定范围内.
通过分析松耦合变压器各参数之间的联系,总结出如图5所示的松耦合变压器设计流程图.从图5可以看出,磁芯几何尺寸和初、次级线圈的设计是关键步骤,通过反复迭代计算,可得到符合要求的设计方案.
3仿真与实验
为验证本文分析得出的励磁电感和漏感计算公式的正确性,运用Maxwell软件仿真,并设计制作了一个松耦合变压器.线圈匝数为Np=75.Ns=200.磁芯参数如表1所示.
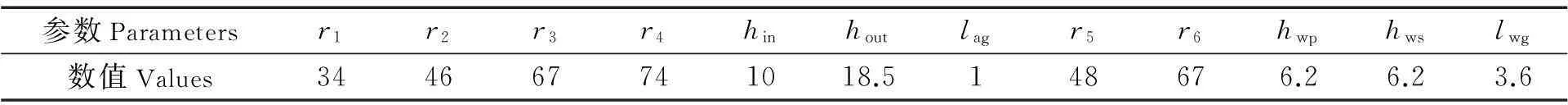
表1 磁芯参数
运用Maxwell 2D在柱状坐标系下建立回转面模型,仿真结果如图6所示.磁通绝大部分沿磁芯闭合,有少许漏磁通,且主要集中在气隙附近.
磁芯材料采用铁氧体PC40,为方便线圈的绕制并且防止漆包线与磁芯摩擦而产生漏电,用尼龙材料制作了一个线圈支架.组装完成后,其实物图如图7所示.采用数字电桥LCR Databridge 2810依照文献[8]中的测量方法测得实验数据.

表2分别为通过公式计算、仿真分析和实物测量得到的励磁电感Lm、初级漏感Llkp、次级漏感Llks和耦合系数k.从表2中可以看出,仿真值与测量值是基本吻合的,计算值和测量值接近,均有少许误差.励磁电感的计算值和仿真值相等,且均小于测量值,误差为4%.初级漏感的计算值与测量值相等,仿真值稍大于测量值,误差为2%.次级漏感的仿真值则比实际上测量值大2%,而次级漏感的计算值与测量值有7%的误差,该误差是由励磁电流Im引起的,式(2)是建立在假设Npip=Nsis之上的,而由式(4)可得Npip>Nsis,因此次级漏感计算值会稍小于实际值.另外,松耦合变压器的加工和组装也会造成一定误差.

表2 电感参数和耦合系数
综上所述,通过公式计算得到的励磁电感和漏感与实际测量值相比有少许误差,其误差精度与仿真值接近,因此可以得出松耦合变压器的励磁电感和漏感的计算公式是正确的、可用的.
4结论
1)松耦合变压器的励磁电感和漏电感的计算公式与实际测量值有0~7%的误差,可用于代替计算机仿真,节省设计时间.
2)通过上述励磁电感和漏感的公式将磁芯和线圈的几何尺寸与电感值联系起来,可以有效的控制漏感,为机构设计和电子元器件的选择提供了准确依据.
3)设计流程图明确了各参数间的联系,为松耦合变压器的设计提供了方向.
4)通过减小励磁电流Im可减小次级漏感计算值与实际值的误差.
5)松耦合变压器不限制转速,初、次级可分离的特性利于实现自动化,十分适合应用于数控机床上,如实现旋转超声加工;其对介质没有要求、不会漏电、不需要频繁维护,具有良好的安全性和稳定性,适合应用于水下设备或者航天航空领域等.因此,松耦合变压器具有广阔的应用前景.
[参考文献]
[1]杨庆新,陈海燕,徐桂芝,等.无接触电能传输技术的研究进展[J].电工技术学报,2010,25(7):6-13.
[2]GREEN A,BOYS J.An inductively coupled high frequency power system for material handling applications[C].Singapore:Proc Int Power Electronics Conf,1993:821-826.
[3]COVIC G,BOYS J,KISSIN M,et al.A Three-phase inductive power transfer system for roadway-powered vehicles[J].Industrial Electronics,IEEE Transactions on, 2007,54(6):3370-3378.
[4]皮钧,王素,冯薇.感应电能传输超声振动刀柄集成系统[J].拖拉机与农用运输车,2010,37(1):20-23.
[5]ESSER A, SKUDELNY H C.A New approach to power supplies for robots[J].IEEE Transactions on Industry Applications,1991,27(5):872-875.
[6]PAPASTERGIOU K D,MACPHERSON D E.An airborne radar power supply with contactless transfer of energy-partI rotating transformer[J].IEEE Transcations on Industrial Electronics,2007,54(5):2874-2884.
[7]SMEETS J P C,ENCICA L,LOMONOVA E A.Comparison of winding topologies in a pot core rotating transformer[C]//IEEE Optimization of Electrical and Electronic Equipment.Basov:IEEE,2010:103-110.
[8]PAPASTERGIOU K D,MACPHERSON D E,FISHER F.Contact-less transfer of energy by means of a rotating transformer[C]//IEEE International Symposium on Industrial Electronics.Dubrovnik,Croatia:IEEE,2005:1735-1740.
[9]SMEETS J,KROP D,JANSEN J,et al.Optimal design of a pot core rotating transformer[C]//IEEE Energy Conversion Congress and Exposition.Atlanta,USA:IEEE, 2010:1735-1740.
[10]SMEETS J,KROP D,JANSEN J,et al.Contactless power transfer to a rotating disk[C]//IEEE International Symposium on Industrial Electronics.Bari:IEEE,2010:748-753.
[11]MCLYMAN C W T.Transformer and inductor design handbook 3rd edition[M].New York:Marcel Dekker,2004.
[12]STUARTT A,KING R J,SHAMSEDDIN H.Rotary transformer design with fixed magnetizing andor leakage inductances[J].IEEE Transactions on Aerospace and Electronic Systems,1986,22(5):565-572.
[13]武瑛,严陆光,徐善纲.新型无接触电能传输系统的稳定性分析[J].中国电机工程学报,2004,24(5):63-66.
[14]杨民生,王耀南,欧阳红林.无接触电能传输系统的补偿及性能分析[J].电力自动化设备,2008,28(9):15-19.
[15]HURLEY W G,GATH E,BRESLIN J G.Optimizing the AC resistance of multilayer transformer windings with arbitrary current waveforms[J].IEEE Transactions on Power Electronics,2000,15(2):369-376.
[16]PAPASTERGIOU K D,MACPHERSON D E.An airborne radar power supply with contactless transfer of energy一partII:converter design[J].IEEE Transcations on Industrial Electronics,2007,54(5):2885-2893.
(责任编辑陈敏英文审校郑青榕)
Parametric Analysis and Design Method of Inductance ofLoosely Coupled Rotating Transformer
WU Cong-miao,PI Jun,LIN Kun-yi
(School of Mechanical and Energy Engineering,Jimei University,Xiamen 361021,China)
Abstract:The inductance of loosely coupled rotating transformer is difficult to calculate because of a relatively oarge air gip.For shortening the design cycle and reducing the step of modeling and simulation,the reluctance model of loosely coupled rotating transformer with pot core and adjacent winding was built and analyzed,and the electric equivalent circuit is also presented.Formulas for calculating magnetizing inductance and leakage inductance was derived based on dimension of the pot core and the coil.According to the relation among parameters,a practical flowchart of design was given.It shows that the comparison results of calculation,simulation and experiment verify the accuracy of predicted results from the formulas for magnetizing inductance and leakage inductance.
Key words:loosely coupling;rotating transformer;air gap;leakage inductance
[文献标志码]A
[中图分类号]TM 401.1
[文章编号]1007-7405(2015)03-0212-06
[作者简介]吴聪苗(1990-),男,硕士生,从事无接触能量传输研究.
[基金项目]国家自然科学基金资助项目(51175225)
[收稿日期]2014-10-20[修回日期]2015-03-30

