一种改进SIFT算法的单目视觉里程计
赵黎明,陈 宁
(集美大学机械与能源工程学院,福建 厦门 361021)
一种改进SIFT算法的单目视觉里程计
赵黎明,陈宁
(集美大学机械与能源工程学院,福建 厦门 361021)
[摘要]针对如何准确获取位姿信息来实现移动机器人的避障问题,提出一种改进SIFT特征点匹配的单目车载视觉里程计算法.首先,为了提高特征点匹配的正确率和实时性,结合主成分分析法和平面极线几何约束,改进了传统SIFI匹配算法,其次,建立合理的移动机器人运动数学模型,得到连续帧间图像信息和移动机器人运动位姿变化的转换关系.试验结果表明,误差仅为1.6%,算法运行时间缩短0.022 s.
[关键词]视觉里程计;改进SIFT;平面极线几何约束
0引言
视觉里程计(VO)是仅利用单个或多个相机的输入信息估计智能机器人的运动信息的过程[1].相比传统的里程计,视觉里程计不会存在编码器读数不准、传感器精度降低或惯导漂移等因素引起的数据误差.
视觉里程计根据研究方法不同可分为基于特征跟踪和基于光流两种方法[2],近年来,随着具有尺度、旋转等不变特性的图像特征点匹配方面的研究不断发展,使得基于特征点的视觉里程计方法成为当前主流方法.文献[3-4]采用了基于SIFT特征点匹配的VO算法,文献[5-6]采用基于SURF特征点匹配的VO算法,SIFT尺度变换效果最好,但实时性最差,SURF速度最快,但尺度变换效果一般.
本文针对两轮差速驱动模型的车辆进行分析,通过单目相机获取平面道路信息,假设车辆在平坦的平面内行驶,以解决单目相机缺少尺度因子问题,车辆的位姿可以用p=(x,y,θ)表示,相机安装位于车体前轴中心,即相机的运动估计与车体运动估计完全一致.采用南加州大学的 Camera Calibration Toolbox for Matlab对相机的内外参数进行标定,采用主成分分析法对SIFT描述子进行改进,结合平面极线几何约束,提高改进SIFT特征点匹配的正确率,通过坐标变换得到车辆位姿变换.
1模型建立
1.1 坐标系建立
图像像素坐标系{I}:固定在图像上的以像素为单位的平面直角坐标系,原点位于图左上角,u,v为像素坐标系横、纵坐标轴,平行于图像物理坐标系X、Y轴.
摄像机坐标系{C}:以针孔相机模型的聚焦中心为原点,相机光轴为Zc轴建立的三维直角坐标系,Xc,Yc与图像物理坐标系平行.
车体坐标系{V}:车体坐标系的原点位于地面,且位于相机坐标系原点的正下方,Xv轴与车辆正前方一致,Zv轴垂直向下.
世界坐标系{W}:作为空间点的参考坐标系,选取具有任意性,在本文中,世界坐标系与拍摄第一帧图像时的车体坐标系{V1}重合.
1.2 数学模型建立
图1表示相机坐标系与图像坐标系的关系.图2指出相机固定在车体的位置关系以及车体坐标系的建立.图3指出相机坐标系与车体坐标系的位置关系.由相机坐标系和车体坐标系的位置关系得到相机外参数Rc和Tc,Tc=[0,0,-h0]T,h0是相机距离地面的高度.前后两帧车体的运动估计与车体坐标系的变化一致,因此问题转化为求解前后两帧车体坐标系之间的变换关系.对此本文需要做如下假设:1)车辆保持在平坦的地面行驶;2)车辆行驶不会发生横向漂移;3)第一帧时刻车体坐标系{V1}与世界坐标系{W}重合.
由假设1)可知车辆姿态可由p=(x,y,θ)表示,其中θ表示在{w}坐标系中车辆与X轴的角度.图4路面上匹配到的改进SIFT特征点M分别在第k帧和第k-1帧图像坐标系{I}的坐标值为(uk,vk)和(uk-1,vk-1),根据相机针孔模型,求得M点在第k帧和第k-1帧车体坐标系内的坐标值,至少匹配到两个特征点,利用线性最小二乘法求得第k帧时刻车体坐标系与第k-1帧时刻车体坐标系的变换矩阵.其中,Δθ表示连续两帧间车体坐标系的角度变化.根据假设3)把车体坐标系原点转换到世界坐标系中,即求得每一时刻车辆的位姿.


2改进SIFT特征点匹配算法
视觉里程计的精度和实时性很大程度上依赖于特征点匹配的准确度以及匹配速度.从Moravec的兴趣点到harris角点,再从SIFT局部特征到SURF局部特征,越来越多的局部视觉特征正在被研究员提出并应用于视觉里程计.SIFT特征在旋转、尺度、仿射和灰度方面具有很好的不变性,但实时性比较差.SURF特征匹配速度最好,但SURF特征在旋转、尺度、仿射、灰度都要差于SIFT.本文对SIFT算法改进以提高其匹配的正确率和实时性,图5为改进SIFT算法的流程图.
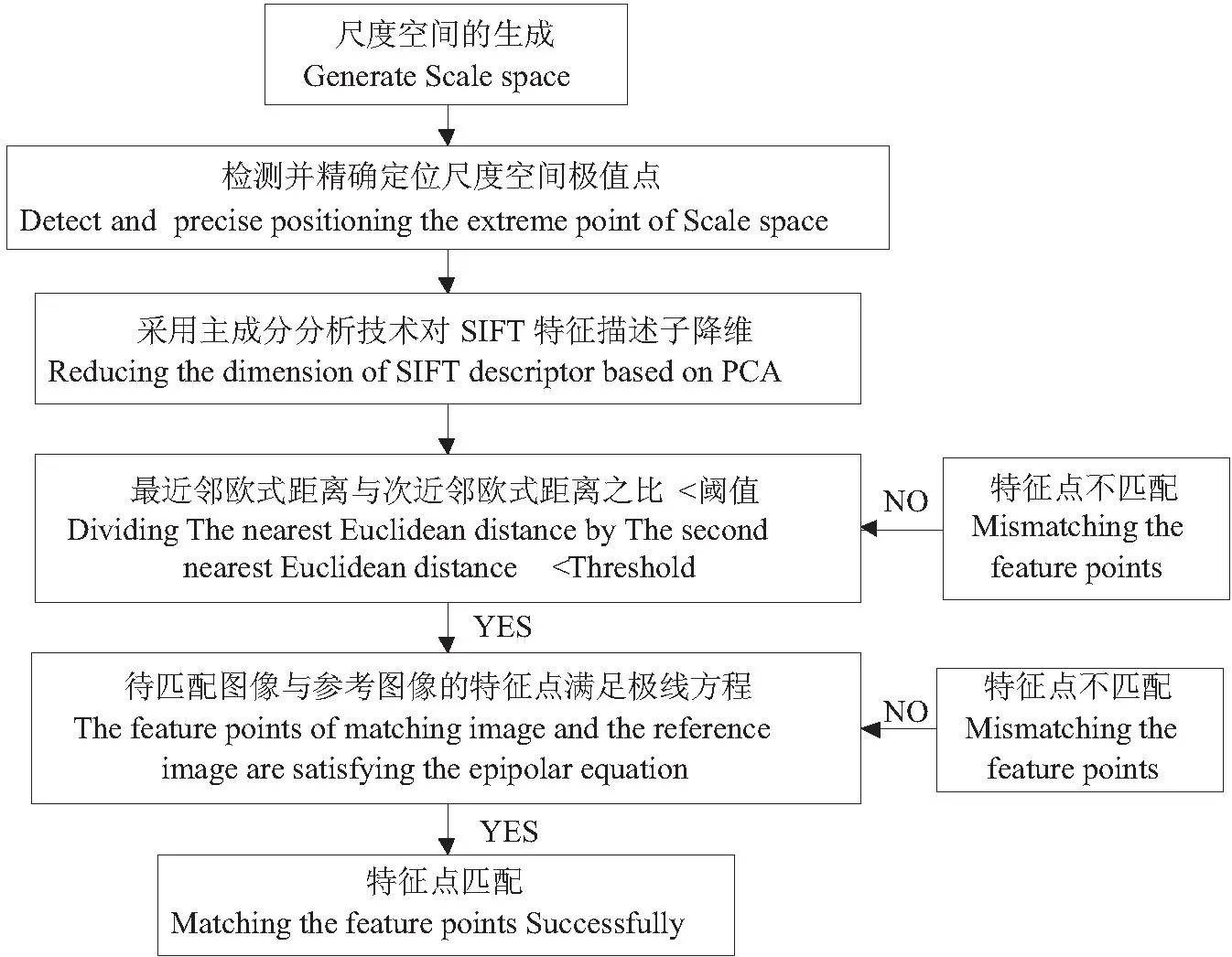
图5 改进SIFT特征点匹配流程图Fig.5 Flow chart of an improved SIFT algorithm
2.1 改进SIFT描述子提取
在图5中改进SIFT算法的第三步,不用原先的4×4×8个描述子,而是在41×41的图像块上计算39×39×2个梯度导数,然后使用主成分分析技术将得到的3042维向量降到36维,改进SIFT描述子将所有描述子中提取出更有区分度,更鲁棒性的特征,从而大幅度提高匹配速率.
2.2 改进SIFT特征点匹配
原始的SIFT特征点匹配,采用优先K-d树进行优先搜索来查找每个特征点的近似最近邻特征点.在这两个特征点中,如果最近的距离除以次近邻距离小于某个比例阈值,则接受这一对匹配点.通过最近邻匹配的阈值进行判断的SIFT匹配算法,通常存在较多错误匹配点,因此还需进行进一步约束,以保障匹配的正确率.
平面极线几何约束是指图像平面与以基线为轴的平面束交的几何,如图6所示.令C、C′分别在第k-1帧和第k帧时刻摄像机的光心位置,C′在第k-1时刻像平面I上的投影为e,C在第k时刻像平面I′上的投影为e′,它们称为极点,像平面I(I′)上通过极点e(e′)的直线称为极线.

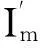

2.3 改进SIFT特征点匹配试验分析
在车辆平移和转弯时采集多组图像进行匹配分析,传统SIFT匹配算法平均耗费时间为0.035 s,改进SIFT匹配算法耗费时间为0.013 s.图8a和图8b分别在平移和转弯时两种算法的匹配正确率.图9a—图9d分别为传统SIFT和改进SIFT算法匹配的效果图.


综合上述分析可得到结论:改进SIFT匹配算法比传统的SIFT算法有更高正确匹配率和实时性.
3单目视觉里程计数学模型求解
单目视觉里程计是指系统通过单目摄像机获取图像序列,经过特征提取、匹配和坐标变换,恢复车辆的运动估计,图10给出了单目视觉里程计的设计流程.

图10 单目视觉里程计设计流程图Fig.10 Flow chart of VO
根据第1部分所建立的数学模型,单目视觉里程计的求解即转化为求解前后两帧车体坐标系之间的变换关系.采用南加州大学的CameraCalibrationToolboxforMatlab对固定在车体上的相机进行线下标定[7],求得相机的内部参数为A,外部参数为相机坐标系和车体坐标系之间的转换关系,由一个旋转矩阵Rc和一个平移矩阵Tc表示.
相机的内部参数:

车体坐标系内任意一点M(xv,yv)在图像上的成像位置(u,v)可以用针孔模型表示:
(1)
根据相机标定结果,结合式(1)得到特征点在{V}中的坐标:
(2)
特征点M在第k帧车体坐标系和第k-1帧车体坐标系之间的转换关系为:
(3)
由式(3)分解得到如下方程组:
(4)
方程组(4)有四个未知数,只需要匹配到两个特征点就能求解.当匹配到的特征点多于两个时,假如匹配到的特征点数为n,可以采用线性最小二乘法求解一组最优解[cos(Δθ),sin(Δθ),Δtx,Δty]T,即为连续帧间车辆位姿变化.
4实验结果与分析
首先搭建基于单目视觉系统的智能车辆试验平台,智能车组成部分由NISbRIO小车、控制器SbRIO-9631单板、超声波传感器、AXISM1013IPCamera、无线路由器DIR-617、移动电源组成.IPCamera固定在NIsbRIO小车前沿,由无线路由器建立一个无线局域网,把小车和IPCamera通过网线与路由器连接,各个设备把IP设置在无线路由器的统一局域网内,实现上位机PC、IPCamera和NIsbRIO小车之间的无线通信,图像实时传回PC机,由PC机做图像处理,从而实时获取小车的运动轨迹.其结构如图11所示.
由于车体比较小且速度在0-0.35m/s的低速状态下运行,因此相机采集速率设置为1Hz,试验小车在校园内行驶117s,实际行驶距离和角度由车轮编码器获取的实时车速和角速度计算得到.最后将视觉里程计得到的小车运动轨迹图与由车轮编码器计算得到的小车运动轨迹进行比较.小车行驶共计30.166 4m.视觉里程计算法计算共计29.686 5m,误差约1.6%.结果如图12所示.
5总结与展望
本文提出了一种精度和实时性都较好的车载单目视觉里程计算法.实验结果中的误差原因有两点,1)由于车体本身的侧滑移导致;2)由于单目相机采用线下标定,而车辆行驶过程中的振动会导致相机外部参数发生改变.
未来车载视觉里程计算法的进一步改进,将会考虑采用相机自标定技术,线上标定技术更适合实时性要求较高的车载视觉里程计.目前大部分视觉里程计的研究都是基于几何方法,即根据标定相机,通过跟踪特征点恢复旋转和平移.将机器学习的方法引入视觉里程计为今后发展的趋势.
[参考文献]
[1]蔡自兴,贺汉根,陈虹.未知环境中移动机器人导航控制研究的若干问题[J].控制与决策,2002,04:385-390.
[2]李宇波,朱效洲,卢惠民,等.视觉里程计技术综述[J].计算机应用研究,2012,08:2801-2805.
[3]SCARAMUZZAD,SIEGWARTR.Apperarance-guidedmonocularomnidirectionalvisualodometryforoutdoorgroundvehicles[J].IEEETransonRobotics,2008,24(5):1015-1026.
[4]SCARAMUZZAD,FRAUNDORFERF,SIEGWARTR.Real-timemonocularvisualodometryforon-roadvehicleswith1-pointransac[C]//ProcofIEEEInternationalConferenceonRoboticsandAutomation.Piscataway,NJ:IEEEPress,2009:4293-4299.
[5]高云峰,李伟超,李建辉.室内移动机器人视觉里程计研究[J].传感器与微系统,2012,02:26-29.
[6]王亚龙,张奇志,周亚丽.基于Kinect的三维视觉里程计的设计[J].计算机应用,2014,08:2371-2374.
[7]JEAN-YVESBOUGUET.CameraCalibrationToolboxforMatlab[EB/OL].(2013-12-02).http://www.vision.caltech.edu/bouguetj/calib_doc/..2014.11
[8]HANWANG,WEIMOU,GERALDSEET,etal.Real-timeVisualOdometryEstimationBasedonPrincipalDirectionDetectiononCeilingVision[J].InternationalJournalofAutomationandComputing,2013,05:397-404.
[9]FRAUNDORFERF,SCARAMUZZAD.VisualodometryPartII:Matching,robustness,optimization,andapplications[J].Robotics&AutomationMagazine,IEEE,2012,19(2):78-90.
(责任编辑陈敏英文审校郑青榕)
An Improved-SIFT Algorithm for a Monocular Visual Odometry
ZHAO Li-ming,CHEN Ning
(School of Mechanical and Energy Engineering,Jimei University,Xiamen 361021,China)
Abstract:This paper presents a robust method for monocular visual odometry capable of accurate position estimation of a mobile robot based on an improved SIFT algorithm.Firstly,for improving the accuracy and performance of real-time of feature points matching,improvements have been made on SIFT algorithm by combining Principal Component Analysis and Epipolar geometric constraint.Secondly,a mathematical model has been developed to determine the relationship between the information of consecutive frames and pose change of mobile robot.Results show that the algorithm brought about an accuracy with relative error less than 1.6%,and the running time of the algorithm reduces 0.022 seconds correspondingly.
Key words:visual odometry;improved-SIFT;epipolar geometric constraint
[文献标志码]A
[中图分类号]TP 24
[文章编号]1007-7405(2015)03-0218-06
[作者简介]赵黎明(1987—),男,硕士生,从事计算机视觉及导航研究.通信作者:陈宁(1972—),男,博士,副教授,从事工程机器人及计算机视觉技术研究.
[基金项目]福建省科技厅省属高校专项课题资助项目(JIC2014024)
[收稿日期]2014-11-02[修回日期]2014-11-27

