简易逻辑教学困惑对高师数理逻辑教学的启示
李杰民
(湛江师范学院 数学与计算科学学院,广东 湛江 524048)
简易逻辑教学困惑对高师数理逻辑教学的启示
李杰民
(湛江师范学院 数学与计算科学学院,广东 湛江 524048)
摘要:高中数学简易逻辑教学中出现的一些“困惑”,对高师院校“数理逻辑”教学的启示有:内容选择上不可忽视基本概念、基本知识;思想方法上要重视形式化、符号化意识的培养;应用方面要加强与高中数学的联系,加强谓词逻辑教学.
关键词:简易逻辑;教学困惑;高师院校;数理逻辑;教学改革
1 高中数学简易逻辑教学中的困惑
高中数学新课程改革十多年来,数学教育类杂志刊载了为数不少的关于逻辑用语教学方面的文章[1~5],这些文章直接或间接地提出了逻辑用语教学方面的一些困惑,典型的一个案例是:文[1]提出了一个关于命题的困惑,后来出现了多篇文章进行解惑,这些解惑的文章由于见解不一,给高中教师又造成了新的困惑,文[5]对此做了一个综述,文[6]对文[5]提出的问题进行了细致的分析,给出了错误的诊断和归因,研究者在文[7]中也给出了该问题的思考与解决方案.总的来说,高中一线教师发表的这些文章虽然选取的例题不尽相同,表现形式各异,但问题的本质或者根源主要集中在:命题的概念,简单命题与复合命题的区分,条件式命题的否定与否命题的关系,含有量词的命题的否定,等等.首先,从以上文献中选择3个典型的困惑予以介绍,下一节再对这些“困惑”进行分析,指出这些困惑对高师院校数理逻辑课程教学的启示.
困惑1:命题的真假[2].
再来看它的逆否命题:若x≥0则x2≥0,显然这是真命题.
如此,不禁产生疑惑:“原命题与其逆否命题同真假”是否还成立?
困惑2:命题的否定与否命题[11].
文[11]的一段话摘录如下:
命题的否定与否命题是截然不同的两个概念,应用时一定不要混淆.例如“若p则q”的否定是“若p则非q”,而“若p则q”的否命题是“若非p则非q”.
困惑3:“或”命题的困惑[1,5].
设p 表示命题:4的平方根是2,q表示命题:4的平方根是-2,则pq 表示命题:4的平方根是2或-2.p是假命题,q 也是是假命题,pq却是真命题,与析取联结词的定义不符,矛盾!
2 对高师数理逻辑教学的启示
数学教育专业的学生毕业后大多数都将从事中学数学教学工作,作为对高中相关模块具有直接指导作用的高师院校的“数理逻辑”课,应该做出怎样的改革和调整来为基础教育服务?研究者认为:高中数学简易逻辑教学出现的困惑对高师院校数理逻辑课程的教学有下面3个方面的重要启示.
2.1内容选择上不可忽视基本概念与基本知识
如何利用有限的学时,传授一些最能让学生受益的知识,这是每个教师在教学中经常会思考的问题,高中简易逻辑教学出现的困惑,再一次启示人们,不可忽视基本概念与基础知识的教学.
现在对“困惑1”做一个分析,大学生怎么判断该命题的真假?研究者将该问题带进课堂,毫无悬念,学生一致判定该命题为真命题,并没有引起困惑,因为有如下的真值表:

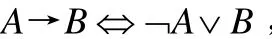
值得一提的是,只有条件式命题才有4种命题可言,某些资料上的练习题没有注意到这一点也给高中师生的教学造成了困扰.
2.2思想方法上要重视形式化和符号化意识的培养
不熟悉数理逻辑的基本概念和基础知识自然是许多论文中出现错误或者产生困惑的根本原因,但是,高中数学新教材“常用逻辑用语”的编写形式化程度低也是一个重要的原因,这一点,美国部分高中教材值得借鉴[8].
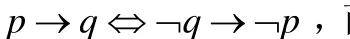
2.3应用方面要加强与高中数学的联系并加强谓词逻辑教学
困惑3是引起争议最大,引发论文最多的一个困惑.要真正讲清楚该困惑,必须要等到学生学完谓词逻辑部分,但是,学生即使学完谓词逻辑,做过一些类似的练习,也不一定能看透该问题的本质,所以,在高师数理逻辑的教学中,应该加强与高中数学的联系,将高中数学一线教师发现的问题引进课堂,在应用中、在解决问题的过程中,让学生感受大学数学理论的威力,体验居高临下的感觉,认真对待大学数学的学习.困惑3的分析难度稍微大一些,通过对该困惑的分析,也启示高师院校数学教育专业要加强谓词逻辑的教学,下面介绍困惑3的分析,供相关的师生参考.
首先,命题“4的平方根是2或-2”应该看作一个原子命题,不要去人为地分解,否则就会掉进困惑的泥潭,当然,另一个困惑又来了,这就是文[5]提出的关于原子命题区分的标准问题,上课介绍的标准是,以定义为准,另补充说明.具有确定真值的陈述句叫做命题,而不能分解为更简单的陈述句的命题称为原子命题[11],这是书本上的定义,经典而简洁,教师要适当加工,补充说明如下:① 不能分解为更简单的陈述句的标准是什么?需要用到现代汉语关于复句的语法知识,所以这不仅仅是一个数学问题.② “不能分解”、“原子命题”这两个概念是相对的,学完谓词逻辑后原子命题也是可以分解的,到那时,不再区分原子命题与复合命题(当然,有新的概念,原子命题函数和复合命题函数).③ 命题逻辑研究的重点并不是命题,而是命题公式(或称合式公式)(Well formed formula)以及命题公式之间的等价关系(范式理论)与蕴涵关系(推理理论).所以,不要在单个命题上纠结,此外,命题逻辑具有局限性,一些问题需要学完谓词逻辑才能解释清楚.

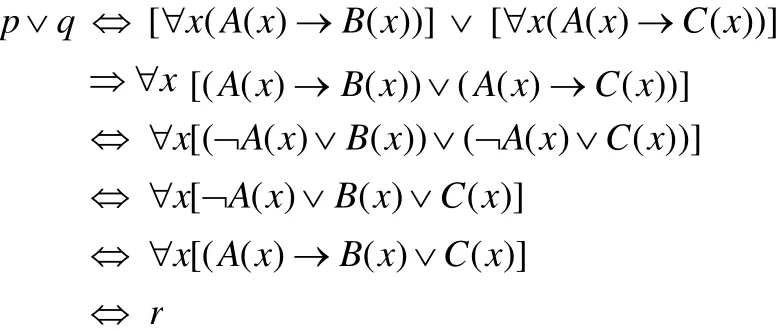
[参 考 文 献]
[1]河北省霸州一中高一数学组.关于命题的困惑[J].中学数学教学参考,2002,(1-2):123.
[2]赵营伟,苗友芝.常用逻辑用语教学过程中的困惑及其反思[J].中学数学,2010,(1):13.
[3]郭随兰.简易逻辑中的常见错误[J].中学数学教学参考,2003,(5):60.
[4]徐彦明.《简易逻辑中的常见错误》中的错误[J].中学数学教学参考,2003,(10):58.
[5]谢全苗.该是新教材编者说话的时候了[J].中学数学教学参考,2005,(6):6.
[6]房元霞,宋宝和.高中简易逻辑中几个概念的辨析及教学建议[J].数学教育学报,2006,15(4):86.
[7]李杰民.高师数学专业数理逻辑教学的一些思考[J].高师理科学科,2011,(4):73.
[8]袁桐.美国中学教材中的逻辑内容[J].数学通报,2002,(2):46.
[9]王林全,林国泰.中学数学思想方法概论[M].广州:暨南大学出版社,2000.
[10]张奠宙,柴俊.关于大学数学教学的一些基本原理[J].高等数学研究,2012,(3):37.
[11]左孝凌,李为鑑,刘永才.离散数学[M].上海:上海科学技术文献出版社,1982.
[责任编校:周学智]
Teaching Perplexity of Simple Logic and Its Enlightenment to Mathematical Logic Teaching in Normal Universities
LI Jie-min
(School of Mathematics and Computational Science, Zhanjiang Normal College, Guangdong Zhanjiang 524048, China)
Abstract:The perplexity appeared from the simple logic teaching in high school has the following enlightenment to the teaching of mathematical logic in normal universities. First, the basic concept and basic knowledge can not be ignored for the selection of teaching content, second, we should attach importance to the cultivating of symbolization and formalization consciousness at the level of ideas, thirdly, for the application, we should strengthen the links with high school mathematics and strengthen the teaching of predicate logic.
Key words:simple logic; teaching perplexity; normal college; mathematical logic; teaching reform
作者简介:李杰民(1973—),男,湖南平江人,讲师,硕士,主要从事离散数学、随机微分方程及其应用研究.
基金项目:广东省特色专业“数学与应用数学”建设项目(粤财教[2011]473号)
收稿日期:2015-03-06
中图分类号:G642
文献标识码:A
文章编号:1004-9894(2015)04-0051-02

