换位形式对1 000 kV同塔双回线路感应电压和电流的影响

王晓彤，班连庚，项祖涛，韩亚楠

(中国电力科学研究院，北京市100192)



换位形式对1 000 kV同塔双回线路感应电压和电流的影响

王晓彤，班连庚，项祖涛，韩亚楠

(中国电力科学研究院，北京市100192)

对不同换位形式下1 000 kV同塔双回线路的感应电压等问题进行了计算和分析。从限制感应电压、潜供电流、线路参数不平衡度的角度看，4段换位优于3段换位但多用1个换位塔；5段B型换位优于6段A型换位且可省1个换位塔；4段换位与6段A型换位的效果大致相当。为此，建议同塔双回线路着重考虑3种换位形式：3段换位(l/3，l/3，l/3)、4段换位(l/6，l/3，l/3，l/6)和5段B型换位(l/6，l/6，l/3，l/6，l/6)。一般不推荐采用2次以上的全循环换位。

1 000 kV；同塔双回线路；换位形式；感应电压；不平衡度；潜供电流

0 引 言

当同塔双回线路一回正常运行、另一回停运检修时，由于回路间存在静电和电磁耦合，将在停运线路上感应出电压和电流。对于重潮流下的1 000 kV同塔双回线路，由于电压等级高、潮流大，其感应电压和感应电流问题可能更严重。根据国家标准化指导性技术文件《GB/Z 24837—2009 1 100 kV高压交流隔离开关和接地开关技术规范》[1]，B类1 100 kV线路接地开关的标准为：静电耦合感应电压为180 kV，静电耦合感应电流50 A；电磁耦合感应电压30 kV，电磁耦合感应电流360 A。关于线路长度、输送功率、回路间距离、线路高抗、相序排列等因素对同塔双回线路感应电压和电流的影响，已有大量研究[2-10]。本文拟研究换位形式(包括换位次数)对同塔双回线路感应电压和电流等问题的影响。

为了进行全面分析，还需考虑换位形式对同塔双回线路的潜供电流、线路参数不平衡度的影响。文献[11]和[12]中已有相关的研究，本文在此基础上补充了部分换位形式，并给出相应的计算结果。

1 同塔双回线路的换位形式

本文考虑了6种可能的相序排列方式[11]。同塔双回线路采用1个全循环换位时，主要有2种典型的换位形式：3段换位(以下简称“1-3”)和4段换位(以下简称“1-4”)；采用2次全循环换位时，则主要有2种典型的换位形式：A型和B型(以下简称“2A”和“2B”)[7]。以逆相序为例，几种典型的换位形式如图1所示。

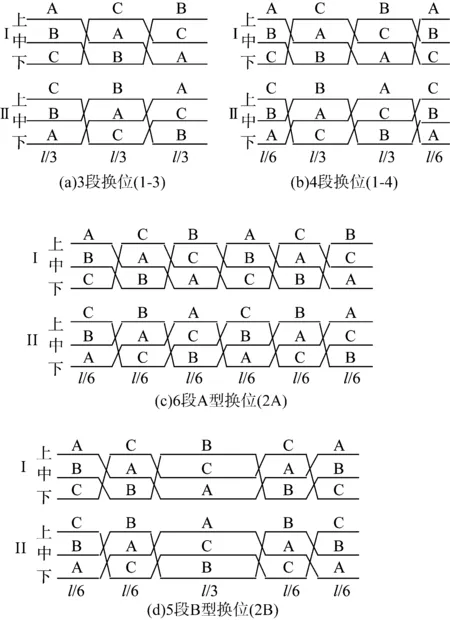
图1 同塔双回线路几种典型的换位形式Fig.1 Typical transposing forms for double-circuit transmission lines

为了消除回路间的正序和负序耦合，还有一种9段换位法[13-14]，见图2。在这种换位形式下，两回线间可近似认为只有零序耦合。

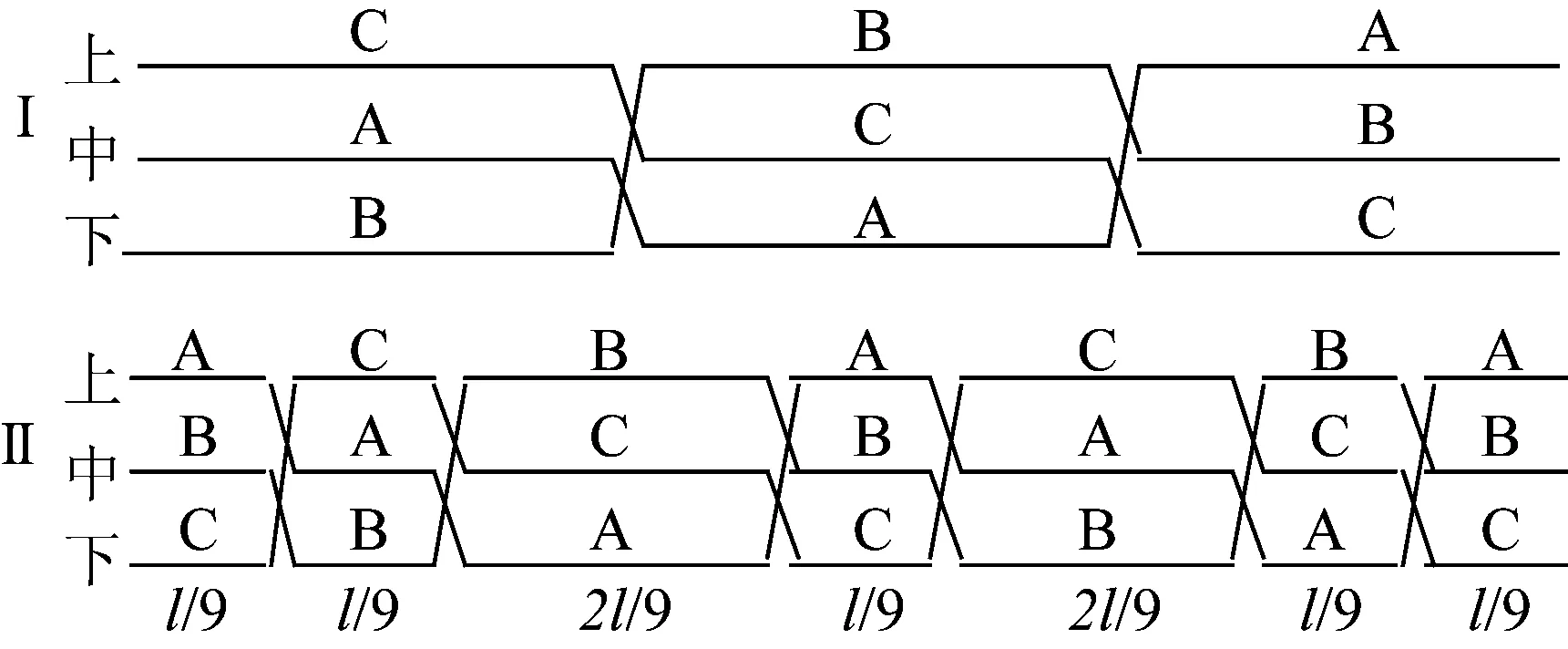
图2 同塔双回线路的9段换位Fig.2 9 segment transposition for double-circuit transmission lines

作为参考，还考虑了另一形式的3段换位(以下简称“1-3X”)[8,13-14]，以及相应的4段换位形式(以下简称“1-4X”)，见图3。该换位形式的第1段相序与图1(a)或1(b)完全相同，只是由于回路II的换位方向不同，使得回路II第2、3段相序有所不同。显然，该换位形式下并不能保证每段线路都是按逆相序排列的。

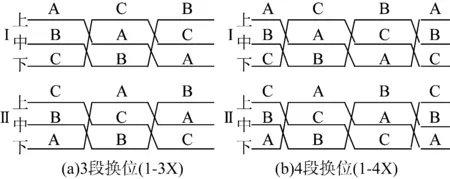
图3 同塔双回线路另一形式的3段或4段换位Fig.3 Another 3 or 4 segment transposition for double-circuit transmission lines

本文以一条400 km的1 000 kV同塔双回线路为例进行研究。线路每回两侧均装设960 Mvar高抗，所采用的线路杆塔及导、地线参数同文献[11]。一回停运时的线路潮流按8 GW考虑。在计算同塔双回线路电气参数的不平衡度、单相重合闸过程中的潜供电流和恢复电压、回路间感应电压和感应电流时，同塔双回线路按6相常规形电路模拟[13,15]。

2 换位形式对静电耦合感应电压和电流的影响

研究表明，其他条件(包括高抗中性点小电抗的取值)相同时，相序ABC/CBA、ABC/BAC、ABC/ACB(即相序1、3、4，均为逆向换位)下的感应电压和感应电流是相同的，而相序ABC/ABC、ABC/BCA、ABC/CAB(即相序2、5、6，均为同向换位)下的计算结果也是相同的。采用逆向换位时的静电耦合感应电压较低，感应电流也较小。

静电耦合感应电压与高抗中性点小电抗的取值有一定的关系。不同换位形式下静电耦合感应电压(取线路首/末端三相电压的最大值，下同)随小电抗值的变化情况如图4所示。需要说明的是，在均匀换位的条件下，回路I、或是回路II退出时，线路感应电压和电流的计算结果差别不大(文中均按回路II退出考虑)。

在一定的参数配合下，图中的等值电路达到谐振状态，则有如下关系。

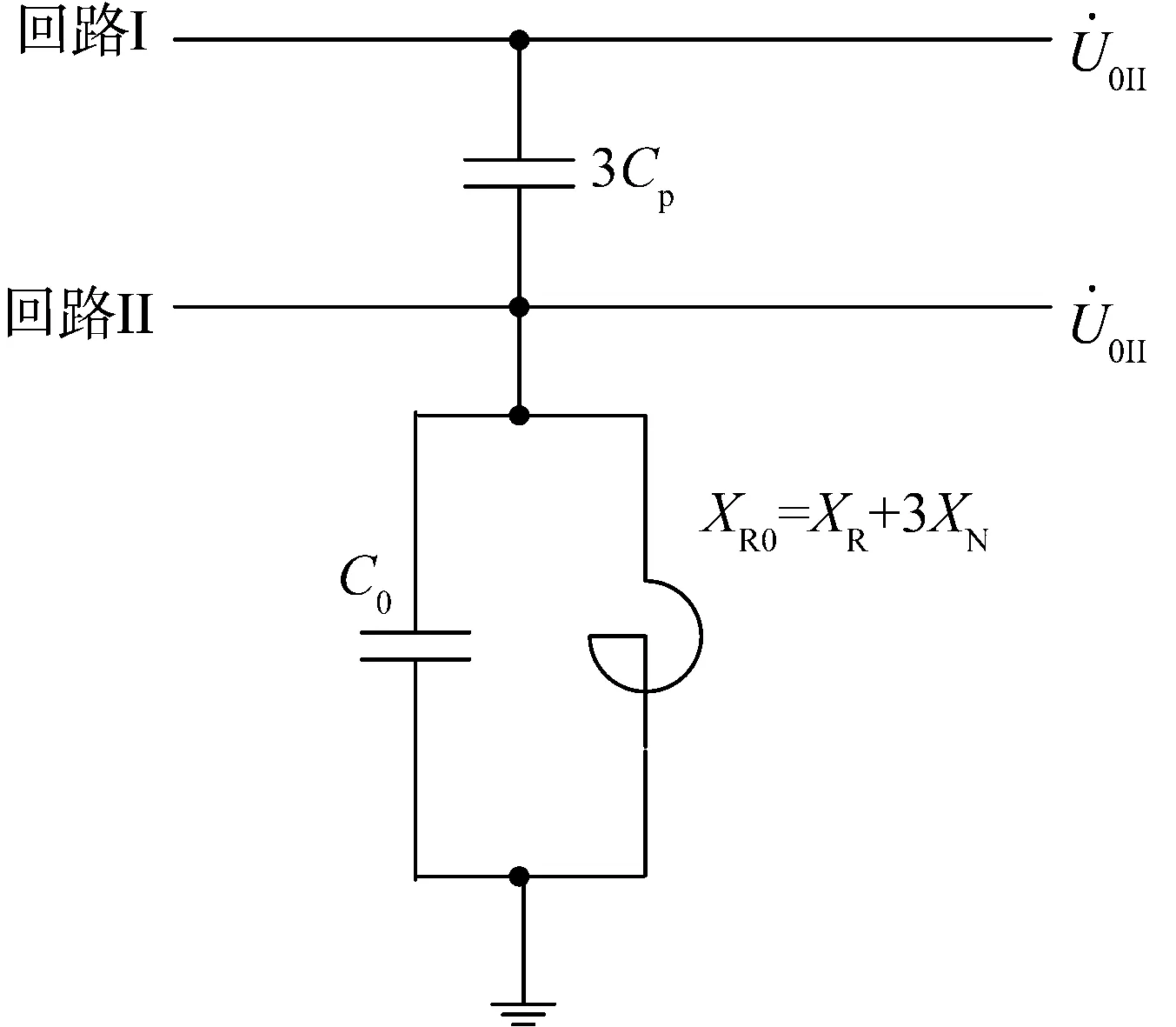
图5 零序等值回路Fig.5 Equivalent circuit for zero sequence

(1)

经推导，零序等值回路达到谐振时的高抗中性点小电抗XN可按式(2)估算

(2)

若线路的两端都有高抗且容量相同，则上式中的XR和XN为相应电抗值的一半。根据上述公式，可得谐振点高抗中性点小电抗为195。根据仿真结果，可知相应的谐振点电抗值约180，与估算值接近。显然，从限制静电耦合感应电压的角度看，高抗中性点小电抗不宜在谐振点的附近取值。

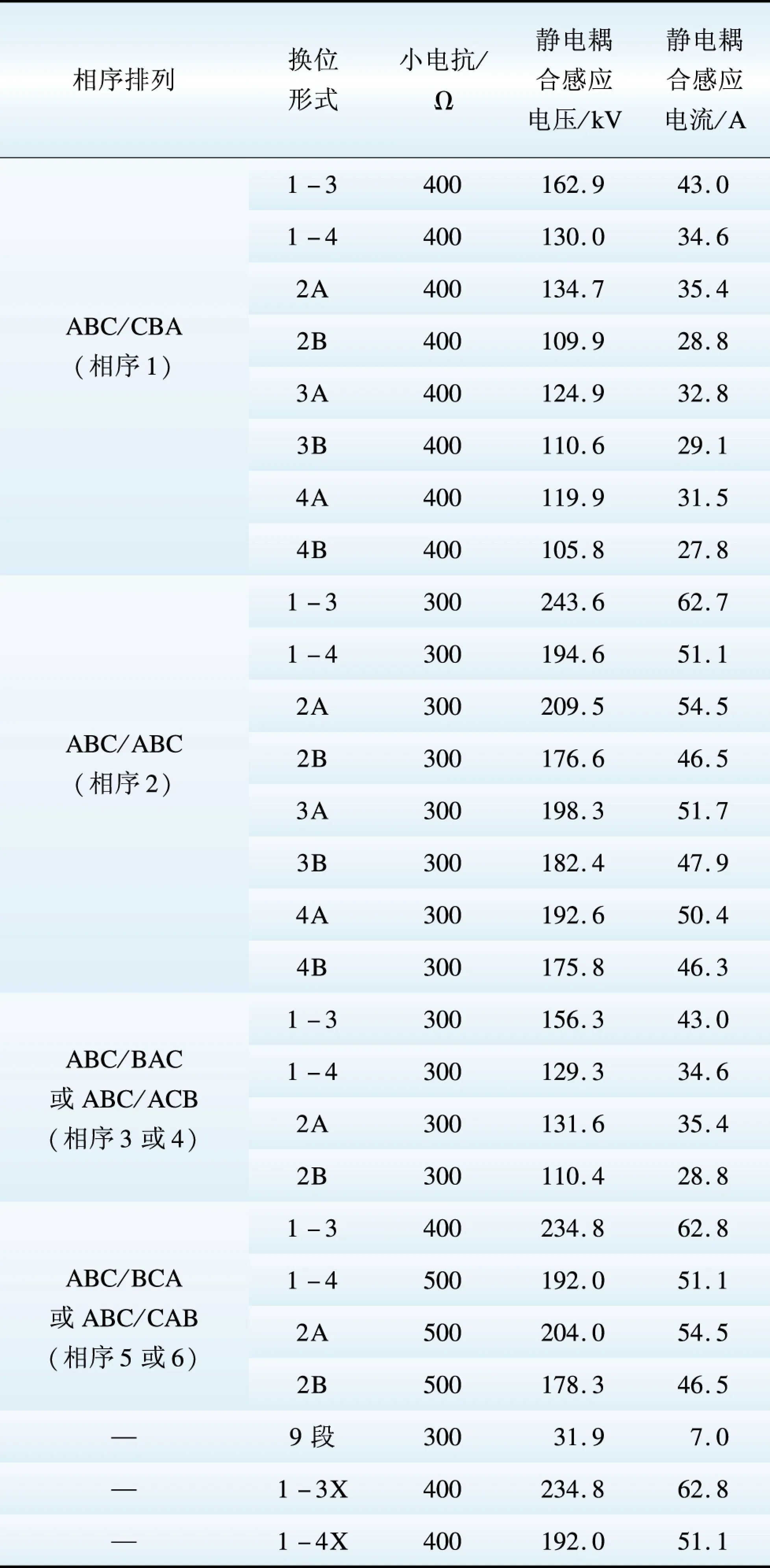
不同换位形式下该1 000 kV同塔双回线路静电耦合感应电压和电流的计算结果如表1所示。其中，“3A”、“4A”分别指3、4次A型全循环换位；“3B”、“4B”分别指3、4次B型全循环换位；“9段”指9段换位。由计算结果可以看出：

(1)从限制回路间静电耦合感应电压和电流的角度看，1个全循环换位时4段换位优于3段换位，而换位次数相同时B型换位优于A型换位；

(2)采用4段换位时的静电耦合感应电压和电流略优于采用6段A型换位时的情况；

(3)由1个全循环换位增加到2个全循环换位，可有效降低静电耦合感应电压和感应电流，继续增加换位次数，则静电耦合感应电压和感应电流降低的幅度很小；

(4)采用9段换位时静电耦合感应电压很低，感应电流也很小；

(5) 采用另一形式3段/4段换位时，两回线路的换位方向相同，其静电耦合感应电压和电流与相序2、5、6下相同。

值得注意的是，采用3次B型全循环换位时，其静电耦合感应电压和感应电流甚至还略高于采用2次B型全循环换位时的情况。在某些情况下，采用3次B型换位时的潜供电流和恢复电压也会高于采用2次B型换位时的情况[11]。

表1 不同换位形式下的静电耦合感应电压和电流

Table 1 Electrostatic coupling induced voltage and current under different transposing forms

3 换位形式对电磁耦合感应电压和电流的影响

不同换位形式下该1 000 kV同塔双回线路电磁耦合感应电压和电流的计算结果如表2所示。

由计算结果可以看出：

(1)从限制回路间电磁耦合感应电压和电流的角度看，1个全循环换位时4段换位优于3段换位，而换位次数相同时B型换位优于A型换位；

表2 不同换位形式下的电磁耦合感应电压和电流

Table 2 Electromagnetic coupling induced voltage and current under different transposing forms

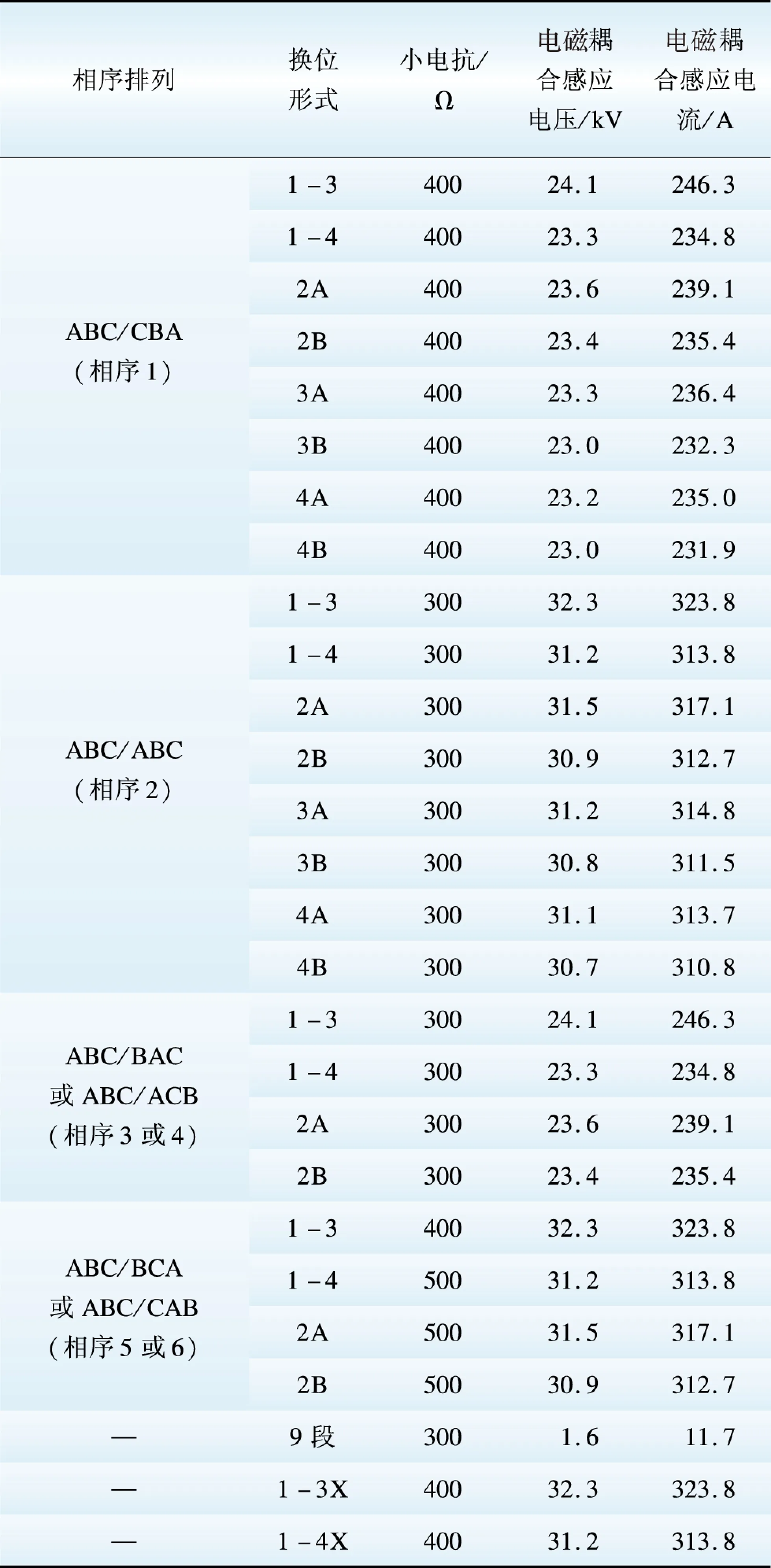
(2)采用4段换位时的电磁耦合感应电压和电流略优于采用6段A型换位时的情况；

(3)增加全循环换位的次数，对回路间电磁耦合感应电压和电流影响不大；

(4)采用9段换位时电磁耦合感应电压很低，感应电流也很小；

(5)采用另一形式3段/4段换位时，两回线路的换位方向相同，其电磁耦合感应电压和电流与相序2、5、6下相同。

4 回路间感应电压和电流的序量分析

不同换位形式下静电耦合感应电压的各序分量如表3所示。其中，线路高抗中性点小电抗的阻值考虑了180，400和1 000时的情况。

表3 不同换位形式下静电耦合感应电压的各序分量

Table 3 Sequence components of electrostatic coupling

induced voltage under different transposing forms

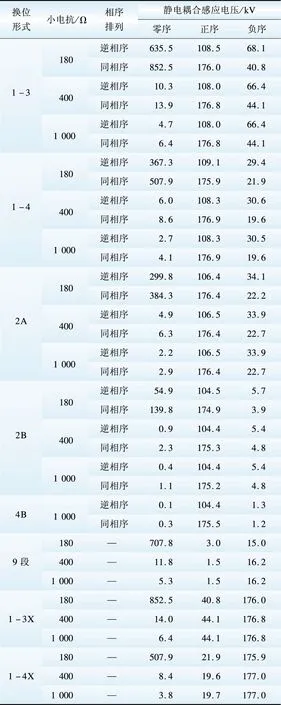
不同换位形式下静电耦合感应电流、电磁耦合感应电压和感应电流的各序分量分别如表46所示。

表4 不同换位形式下静电耦合感应电流的各序分量

Table 4 Sequence components of electrostatic coupling induced current under different transposing forms

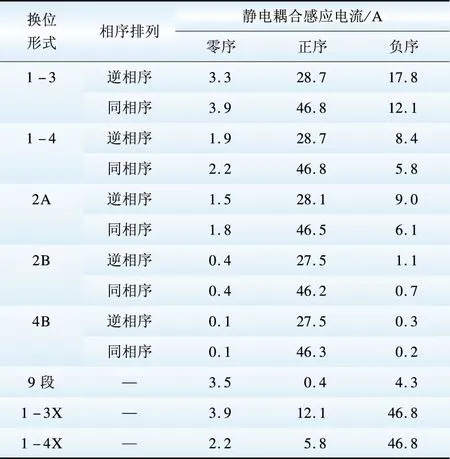
表5 不同换位形式下电磁耦合感应电压的各序分量Table 5 Sequence components of electromagnetic coupling induced voltage under different transposing forms

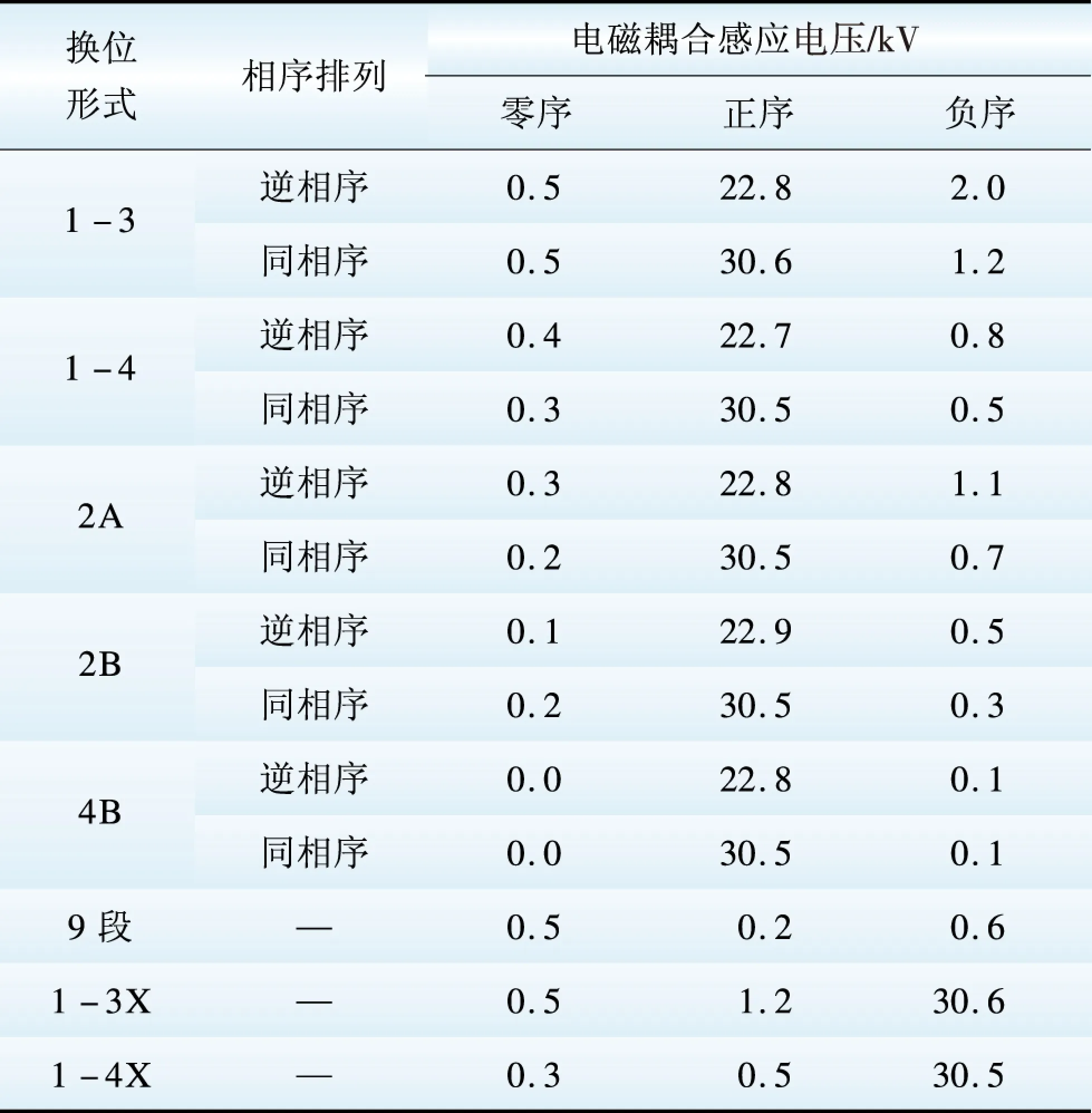
由计算结果可以看出：

(1)除了高抗中性点小电抗在谐振点附近外，静电耦合感应电压的零序分量通常较小。

(2)静电耦合感应电压/电流中的零序或负序分量所占比重较大，这是因为静电耦合感应电压/电流与线路并联电容相关。由于线路高抗的存在，会显著增加静电不平衡度[16]，从而增加了静电耦合感应电压/电流中的零序或负序分量。因此，增加线路全循环换位的次数(即减少零序和负序分量)对静电耦合感应电压和电流有一定的影响。

表6 不同换位形式下电磁耦合感应电流的各序分量

Table 6 Sequence components of electromagnetic coupling induced current under different transposing forms

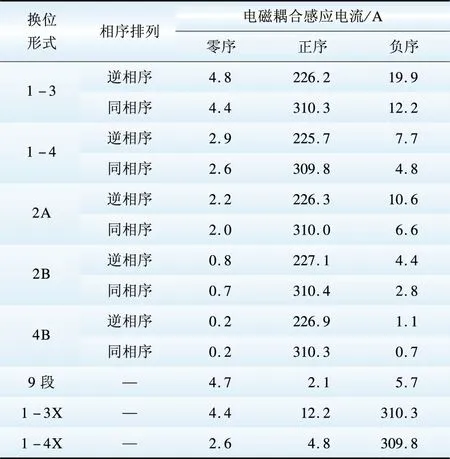
(3)电磁耦合感应电压/电流中的零序或负序分量所占比重很小。这是因为，电磁耦合感应电压/电流与线路串联阻抗(包括电阻、电感)相关。由于线路参数的电磁不平衡度相对较低(与考虑线路高抗后的静电不平衡度相比)，从而零序和负序分量所占比重较小。因此，增加线路全循环换位的次数(即减少零序和负序分量)对电磁耦合感应电压和电流影响不大。

(4)采用9段换位时，正序分量很小。这是因为采用9段换位法能较好地消除回路间的正序耦合。

(5)采用另一形式3段/4段换位时，其序量情况与同相序下3段/4段换位时接近，只是正序和负序分量的数值交换了。出现这种现象，与该换位形式下正序和负序间的交叉耦合有关[13-14]。

5 换位形式对潜供电流和恢复电压的影响

不同换位形式下同塔双回线路的潜供电流和恢复电压(计算条件同文[11])如表7所示。

由计算结果可以看出：

(1)采用4段换位时的潜供电流和恢复电压介于3段换位和5段B型换位之间，与6段A型换位时接近或略优；

表7 不同换位形式下的潜供电流和恢复电压

Table 7 Secondary arc current and recovery voltage under different transposing forms

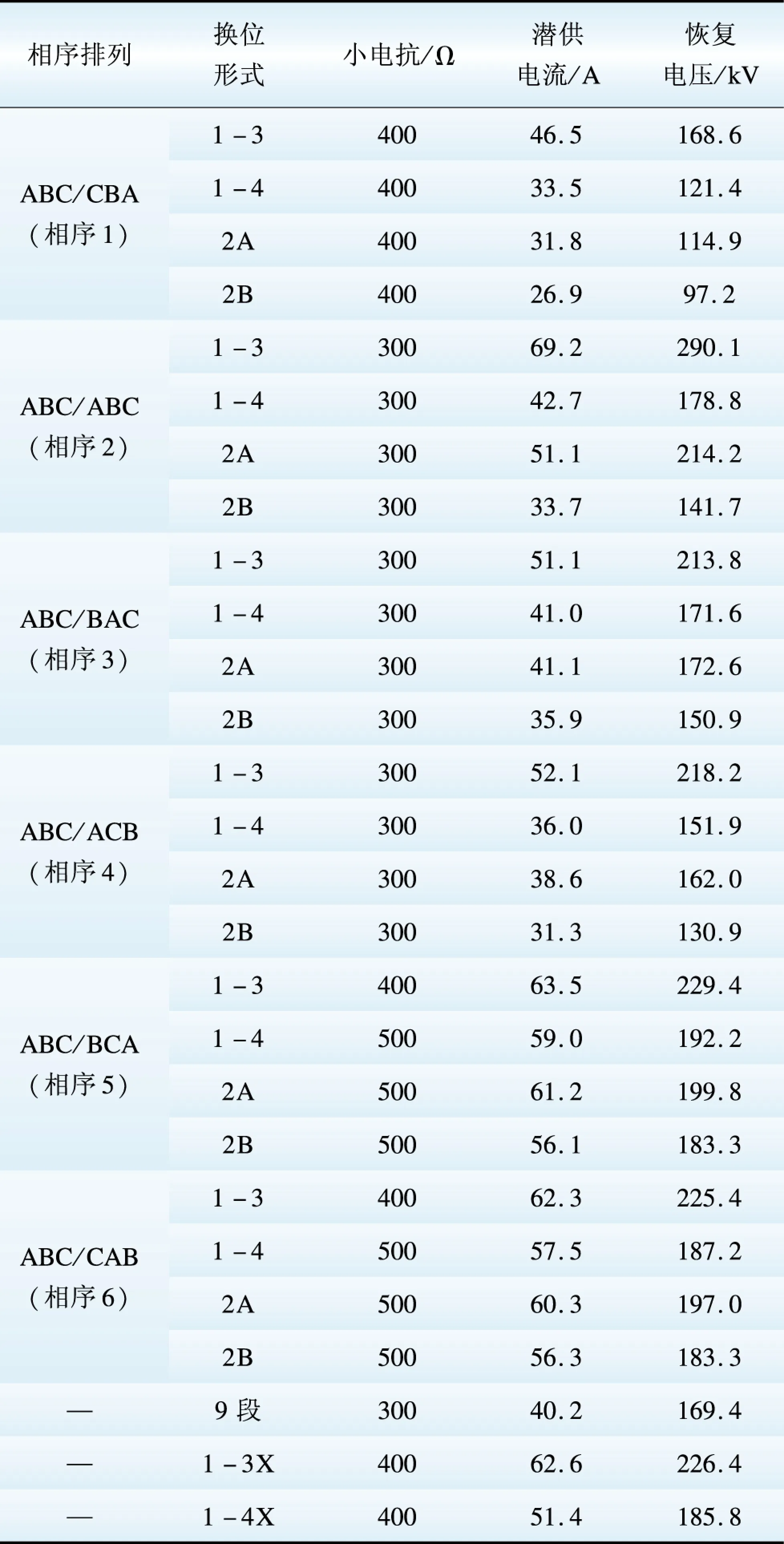
(2)采用9段换位对限制潜供电流的效果并不明显，甚至还要大于逆相序下采用4段换位时的情况；

(3)采用另一形式3段/4段换位时潜供电流大于逆相序下采用3段/4段换位时的情况。

6 换位形式对线路参数不平衡度的影响

以电磁不平衡度为例，不同换位形式下同塔双回线路参数的不平衡情况如表8所示。

由计算结果可以看出：

(1)采用4段换位时线路参数的不平衡度介于3段换位和5段B型换位之间，与6段A型换位时接近；

表8 不同换位形式下的电磁不平衡度

Table 8 Electromagnetic unbalance degree under different transposing forms

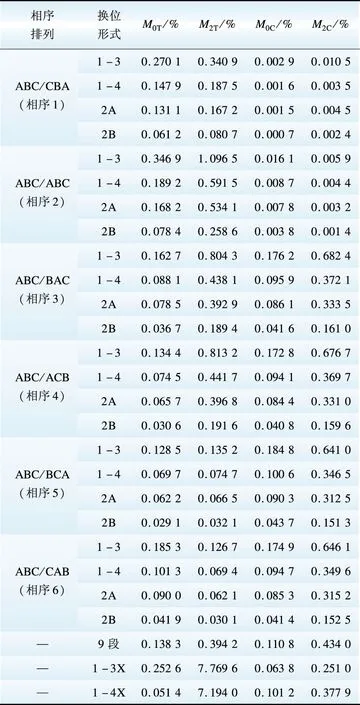
(2)采用9段换位时，线路参数的不平衡度甚至还不及逆相序下采用3段换位时的情况；

(3)采用另一形式3段/4段换位时，其负序直通型不平衡度远高于其他几种换位形式。由于直通型不平衡度与母线电压的不平衡度有一定的相关性[7]，故该换位形式下负序电压不平衡度也较高[8]。

7 结 论

(1)从限制回路间感应电压、潜供电流、线路参数不平衡度的角度看，4段换位优于3段换位，但多用1个换位塔；5段B型换位优于6段A型换位，且节省1个换位塔；采用4段换位与6段A型换位的效果大致相当，介于3段换位和5段B型换位之间。

(2)由1个全循环换位增加到2个全循环换位，可有效降低线路参数的不平衡度、潜供电流和恢复电压、静电耦合感应电压和感应电流；继续增加换位次数，则潜供电流和恢复电压、静电耦合感应电压和感应电流降低的幅度很小；增加全循环换位的次数对回路间的电磁耦合感应电压和感应电流影响不大。

(3)采用9段换位时回路间感应电压很低，感应电流也很小；但在线路参数的不平衡度、潜供电流和恢复电压方面均不及逆相序下采用4段换位时的情况，且需8个换位塔，故在实际工程中很少采用。

(4)采用另一种形式3段/4段换位时的负序直通型不平衡度远高于其他几种换位形式，且感应电压、潜供电流等计算结果均明显高于逆相序下采用3段/4段换位时的情况，故不推荐该换位形式。

综上所述，从限制同塔双回线路参数的不平衡度、潜供电流和恢复电压、感应电压和感应电流的角度看，建议着重考虑3种换位形式：3段换位(l/3，l/3，l/3)、4段换位(l/6，l/3，l/3，l/6)和5段B型换位(l/6，l/6，l/3，l/6，l/6)。一般不推荐采用2次以上的全循环换位。

[1]GB/Z 24837—2009 1 100 kV高压交流隔离开关和接地开关技术规范[S].北京：中国标准出版社，2009.

[2]张文亮，谷定燮，方文弟，等.洪龙500 kV带高抗同杆双回线路间的感应作用研究[J].高电压技术，2002，28(2)：10-12. Zhang Wenliang，Gu Dingxie，Fang Wendi, et al.A study on induced effect between the 500 kV HongLong double circuit transmission lines with HV shunt reactor[J].High Voltage Engineering, 2002, 28(2)：10-12.

[3]郭志红，姚金霞，程学启，等.500 kV 同塔双回线路感应电压、电流计算及实测[J].高电压技术，2006，32(5)：11-14. Guo Zhihong，Yao Jinxia，Cheng Xueqi，et al.Study and measurement of induced voltage and current for 500 kV double-circuit line on same tower[J].High Voltage Engineering，2006，32(5)：11-14.

[4]韩彦华，黄晓民，杜秦生.同杆双回线路感应电压和感应电流测量与计算[J].高电压技术，2007, 33(1)：140-142, 159. Han Yanhua，Huang Xiaomin，Du Qinsheng.Induced voltage and current on double circuits with same tower[J].High Voltage Engineering, 2007, 33(1)：140-142, 159.

[5]胡丹晖，涂彩琪，蒋伟，等.500 kV 同杆并架线路感应电压和电流的计算分析[J].高电压技术，2008，34(9)：1927-1931. Hu Danhui，Tu Caiqi，Jiang Wei，et al.Calculation of inductive voltage and current for 500 kV double circuits transmission lines on single tower[J].High Voltage Engineering，2008，34(9)：1927-1931.

[6]陈亚伦，李志国.伊敏—冯屯500 kV同塔双回线不平衡度、感应电流及潜供电流研究[J].电网技术，1995，19(6)：13-17. Chen Yalun，Li Zhiguo.Study of unbalance factor and induced current for Yimin-Fengtun 500 kV double-circuit tower line[J].Power System Technology，1995，19(6)：13-17.

[7]王晓彤，林集明，班连庚，等.1000kV同塔双回线路不平衡度及换位方式分析[J].电网技术，2009，33(5)：1-5. Wang Xiaotong，Lin Jiming，Ban Liangeng，et al.Analysis on unbalance factor and transposing modes for 1000kV double-circuit transmission lines on the same tower[J].Power System Technology，2009，33(5)：1-5.

[8]陈恺，林章岁.1 000 kV特高压同塔双回输电线路相序排列和换位方式研究[J].电力与电工，2011，31(3)：11-14. Chen Kai，Lin Zhangsui.Study on phase sequence arrangement and transposing modes for 1 000 kV UHV double circuit transmission lines[J].Electric Power and Electrical Engineering，2011，31(3)：11-14.

[9]林莘，李学斌，徐建源.特高压同塔双回线路感应电压、电流仿真分析 [J].高电压技术，2010, 36 (9)：2193-2198. Lin Xin, Li Xuebin, Xu Jianyuan.Simulation and analysis of induced voltage and current for UHV double circuit transmission lines on the same tower[J].High Voltage Engineering, 2010, 36 (9)：2193-2198.

[10]李宝聚，周浩.1 000 kV 同塔双回线路感应电压和电流的计算分析[J].电网技术，2011，35(3)：14-19. Li Baoju, Zhou Hao.Calculation and analysis on induced voltage and current of 1 000 kV transmission line adopting structure of double circuit on the same tower [J].Power System Technology，2011，35(3)：14-19.

[11]王晓彤，项祖涛，班连庚，等.重潮流下1 000 kV同塔双回长线路的潜供电流及其限制措施[J].电网技术，2013，37(11)：3001-3006. Wang Xiaotong，Xiang Zutao，Ban Liangeng，et al.Secondary arc current in 1 000 kV double-circuit long-distance AC transmission lines on the same tower under heavy power flow and its restrictive measures[J].Power System Technology，2013，37(11)：3001-3006.

[12]王晓彤，班连庚，项祖涛，等.换位次数对同塔双回线路参数不平衡度的影响[J].智能电网，2014，2(9)：23-28. Wang Xiaotong，Ban Liangeng，Xiang Zutao，et al.Influence of transposing time on unbalance factors of electrical parameters of double-circuit transmission lines on the same tower[J].Smart Grid，2014，2(9)：23-28.

[13]Dommel H W.电力系统电磁暂态计算理论[M].北京：水利电力出版社，1991：65-68,78.

[14]施围，郭洁.电力系统过电压计算[M].西安:西安交通大学出版社，2006.

[15]王晓彤，林集明，班连庚，等.稳态计算中2种EMTP线路模型的比较研究[J].中国电力，2009，42(12)：15-19. Wang Xiaotong, Lin Jiming, Ban Liangeng, et al.Comparison between two kinds of EMTP line models in steady-state calculations [J].Electric Power，2009，42(12)：15-19.

[16]王晓彤，班连庚，郑彬.750 kV同塔双回紧凑型输电线路潮流不平衡及导线换位研究[R].北京:中国电力科学研究院，2008.

(编辑：刘文莹)

Influence of Transposing Form on Induced Voltage and Current in 1 000 kV Double-Circuit Transmission Lines

WANG Xiaotong, BAN Liangeng, XIANG Zutao, HAN Yanan

(China Electric Power Research Institute, Beijing 100192, China)

The problems such as induced voltage and so on in 1 000 kV double-circuit transmission lines on the same tower were calculated and analyzed under different transposing forms. From the viewpoint of restricting induced voltage, secondary arc current and unbalanced degree of line parameters, 4 segment transposition is better than 3 segment transposition, but 1 more transposition tower is needed; while 5 segment type B transposition is better than 6 segment type A transposition and 1 transposition tower is saved. The effects of 4 segment transposition and 6 segment type A transposition are similar. Therefore, three kinds of transposing forms should be emphatically considered for double-circuit transmission lines on the same tower: 3 segment transposition (l/3,l/3,l/3)), 4 segment transposition (l/6,l/3,l/3,l/6)) and 5 segment type B transposition (l/6,l/6,l/3,l/6,l/6). It is not recommended to use more than 2 complete cycle transpositions in general.

1 000 kV; double-circuit transmission lines on the same tower; transposing form; induced voltage; unbalanced degree; secondary arc current

国家电网公司科技项目(SGTGYJSFW(2012)378)。

TM 743

A

1000-7229(2015)05-0037-08

10.3969/j.issn.1000-7229.2015.05.007

2014-12-30

2015-04-01

王晓彤(1972)，女，博士，教授级高级工程师，主要研究方向是电力系统电磁暂态仿真；

班连庚(1960)，男，硕士，教授级高级工程师，主要研究方向是电力系统电磁暂态仿真；

项祖涛(1976)，男，博士，高级工程师，主要研究方向是电力系统电磁暂态仿真；

韩亚楠(1984)，女，硕士，工程师，主要研究方向是电力系统电磁暂态仿真。