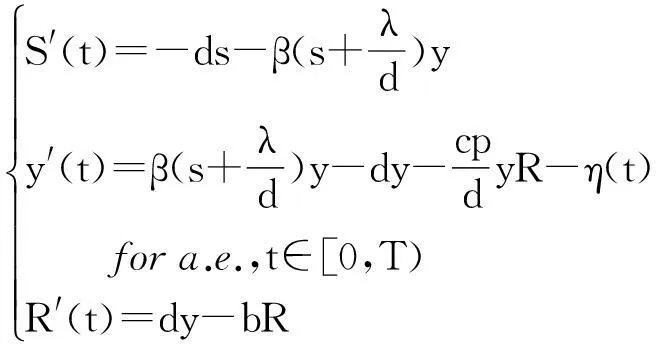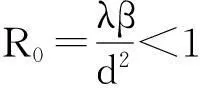非连续治疗策略对一类病毒传染病全局动力学模型的影响

李　迅，孙光讯

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)



非连续治疗策略对一类病毒传染病全局动力学模型的影响

李迅，孙光讯

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)

摘要：本文主要研究了一个具有非连续治疗策略的病毒传染病动力学模型。定义了基本再生数R0，利用微分包含的相差知识分析研究了该细胞病毒免疫反应的平衡点存在性问题。当R0>1时，通过构造相应的Lyapunov函数可证明模型满足初始条件的每一个解都是在有限时间内全局收敛于地方病平衡点；当R0<1时，模型在有限时间内收敛于无病平衡点。

关键词：病毒动力学模型；非连续治疗策略；有限时间全局收敛；Lyapunov函数

数学模型在帮助理解病毒动力学方面扮演了一个重要的角色，如细胞病毒动力学问题[1-2]，但只讨论了连续的微分方程，即细胞病毒的治疗是连续的。但是在实际治疗过程中，由于一些人为或者自然因素的影响，受感染的病毒数量会出现突然的增加，这就是非连续的治疗现象。以下研究非连续治疗策略对病毒传播的影响。

1模型的建立

文献[1]主要研究了如下的微分模型

在上述模型中引进一个非连续的函数h(y)，得到如下的右端不连续微分方程

(1)

这里的参数都是正参数，其中x(t)表示易感染细胞，xy(t)表示已感染细胞(可产生病毒粒子)，z(t)表示免疫细胞数量，βxy表示细胞感染速率，pz表示免疫反应的强度，函数h(y)表示治愈率，λ表示细胞的自然再生率，d表示细胞的自然死亡率。为了讨论更一般的情况，允许函数h(y)存在一些跳跃间断点，下面给出一些假设：

(H1) h(y)=φ(y),φ∶R+→R+是一个非减函数且在每一个紧致区间内至多有有限个跳跃间断点。

备注1不失一般性，假设函数φ在0处连续，否则将φ在0处的值定义为φ(0+)，这对模型(1)没有任何影响。模型(1)的初始条件：

x(0)=x0≥0,y(0)=y0≥0,

z(0)=z0≥0

(2)

为了方便讨论模型(1)解的问题，需引入右端不连续微分方程的Filipov解的定义，考虑如下右端不连续微分方程

x′(t)=f(t,x(t))

(3)

其中f关于变量是可测的且是局部有界的。

定义1[3]考虑如下的集值映射

(4)

设(x(t),y(t),z(t))，t∈[0,T)，T∈(0,+∞)是模型(1)的一个Filipov定义下的解，且该解在[0,T)的任一个子区间[t1,t2]上都是一致连续的，则由定义1知(x(t),y(t),z(t))满足下面的微分包含

(5)

(6)

备注2对于上述的可测函数m(t)满足以下两个条件：

(1)m(t)是除[0,T)内一系列零测度集以外的函数，由(x(t),y(t),z(t))唯一确定的测度函数；

(2)当且仅当(x(t),y(t),z(t))对所有的t∈[0,T)连续可微时，m(t)对所有的t∈[0,T)是连续的。

推论1假设(H1)是成立的，令(x(t),y(t),z(t))是模型(1)带有初值条件x(0)=x0≥0,y(0)=y0≥0,z(0)=z0≥0在[0,T)上的一个解，这里的T∈(0,+∞)。由此可得x(t)≥0，y(t)≥0，x(t)≥0，t∈[0,T)。

证明由对模型(1)定义下的Filipov解的理解，可得(x(t),y(t),x(t))微分包含(5)的一个解。由微分方程(5)，可以得到

再结合x(0)=x0≥0,则能得到x(t)≥0，t∈[0,T)。

(7)

假设y0=0，则从(7)可以得到对任意的t∈[0,T)有y(t)=0。假如y0>0，可得对任意的t∈[0,T)有y(t)>0；否则，令t1=inf{t∶y(t)=0}，则有t1>0并且y(t1)=0。因为y(t)在[0,T)上是连续的，则存在一个正的参数θ，对t∈[t1-θ,t1]使得t1-θ>0，且0

这就产生了矛盾，因此，可得对任意的t∈[0,T)有y(t)>0。

类似于y(t)>0的证明，也可得对任意的t∈[0,T)有z(t)>0。

2平衡点

为得到模型(1)的平衡点，先来定义它的一个常数解(x,y,z)=(x*,y*,z*),t∈(0,+∞)。显然，若(x*,y*,z*)是模型(1)的平衡点，当且仅当

(8)

同时存在一个ξ满足

(9)

这里的常数ξ*是唯一的，且ξ*=βx*y*-dy*-py*z*。

当假设(H1)成立时，为了得到模型(1)的平衡点，接下来讨论如下的微分包含：

(10)

(11)

由(11)式可以得到如下微分包含

(12)

令

证明首先来证微分包含(12)式存在一个正解。因为R0>1，则g(0)>φ(0)>0，又因为g(y)是单调递减函数，φ(y)关于y是非单减的函数。另外，g(y)≤0当且仅当

(13)

将(13)式的两个方程相减可得，

定理1当基本再生数R0>1时，模型(1)存在唯一的地方病平衡点E*=(x*,y*,z*)满足(11)式，其中y*是由引理1确定的唯一正解。

3有限时间内的全局收敛

这一节主要通过构造合适的Lyapunov函数来证明模型(1)全局收敛于地方病平衡点E*和无病平衡点E0，为了证明这个结论，首先给出下面的假设，

(H2)假设R0>1，φ(y)在y*处有一个跳跃间断点，其中y*是由引理1确定的唯一正解。另外取η*=βx*-d-pz*∈(φ((y*)-),φ((y*)+))，根据(H2)可以定义θ∶=min{φ((y*)+)-η*,η*-φ((y*)+)}>0

定理2在假设(H1),(H2)都成立的条件下，模型(1)所有满足初始条件(2)下的每个解都在有限时间内全局收敛于平衡点E*=(x*,y*,z*)。也即对于所有的

都有

(x,y,z)=(x*,y*,z*),t∈(0,+∞)

其中V0(x(0),y(0),z(0))=

(14)

构造下面的Lyapunov函数

(15)

其中γ是一个正的常数，定理后面将给出它的取值范围。很容易发现V1(S(t),I(t),R(t))是一个正则函数，当(S(t),I(t),R(t))≠0时，V1(S(t),I(t),R(t))>0且V1(0,0,0)=0;当S→+∞或I→+∞或R→+∞时，V1(S(t),I(t),R(t))→+∞，则有

[η(t)-η*](I+y*)}≤-ds2+γβS[η(t)-η*]-

将上式两边从0到t积分可得

0≤V1(S(t),I(t),R(t))≤

(H3)h∶R+→R+是一个非单调递减函数，且在每一个紧致区间内至多有有限个间断点，另外h(0)=0但是h(y)在y=0处不连续。

V2(S(0),I(0),R(0))=

这也就是说病毒将在有限时间内灭亡。

(16)

(17)

构造一个新的Lyapunov函数：

V2(S(t),y(t),R(t))=

(18)

由推论1可知，模型(1)在初始条件(2)下的任意解(x(t),y(t),z(t))都是非负的，则函数V2(S(t),y(t),R(t))是一个正则函数，当(S,y,R)≠0时，V2(S(t),y(t),R(t))>0；而仅当(S,y,R)=0时，V2(S(t),y(t),R(t))=0。对(18)式求导可得，

由此可得

将上式两边从0到t积分可得

0≤V2(S(t),y(t),R(t))≤

参考文献:

[1]Y.Nakata,Y.Enatsu.Complete global dynamics of a delayed viral infection model with lytic and nonlytic effectors [J].SEMA Journal,2012,60:27-50.

[2]Yunfei Li,Rui Xu,Zhe Li,et al.Global dynamics of a delayed HIV-1 infection model with CTL immune response [J].Discrete Dynamics in Nature and Society,2011,2011:1-13.

[3]马知恩，周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2001.

[4]J.P.Aubin,A.Cellina.Differential inclusions:set-valued maps and viability theory[M].Berlin:Springer Verlag,1984.

[5]M.Forti,M.Grazzini,P.Nistri,et al.Generalized lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations[J].Phys.D.,2006,214:88-89.

[6]Zhengyuan Guo,Lihong Huang.Impact of discontinuous treatments on disease dynamics in an SIR epidemics mode[J].Mathematical Biosciences and Engineering,2012,9(1):97-110.

Impact of Discontinuous Treatments on Global Dynamics of a Viral Infection Model

LI Xun, SUN Guang-xun

(College of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

Abstract:In this article,we mainly study the impact discontinuous treatments on global dynamics of a viral infection model. By calculating the model equation,we define the basic reproductive rate R0>1, and structure appropriate Lyapunov function and achieve the convergence to the endemic equlibrium in finite time,if R0<1, we also can get convergence to the disease equilibrium in finite time.

Key words:viral infection dynamic model,discontinuous treatment,convergence in the finite time,Lyapunov function

文章编号：1007-4260(2015)03-0014-05

中图分类号：O231.9

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.005

作者简介：李迅，男，安徽全椒人，安徽师范大学数学计算机科学学院硕士研究生，研究方向为应用数学。

基金项目：安徽高校省级优秀青年人才基金重点项目(2011SQRL022ZD)。

收稿日期：2015-02-03

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.005.html