一类特殊图的顶点染色数

张 祥 波

(临盘中学，　山东　临邑　251507)



一类特殊图的顶点染色数

张 祥 波

(临盘中学，山东临邑251507)

摘要：如果图G含有的所有最大团存在公共顶点，且公共顶点的个数为k，就称此图为第k类图。据此，本文给出了研究图的顶点染色的一种新方法，并以此研究了一类特殊图的顶点染色及一些图的顶点染色数。

关键词：最大团；顶点染色数；第k类图；图的厚度

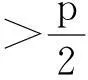
1预备知识

关于文中所用术语和简称，以下不加说明地沿用文献[19]。文中仅考虑无向简单图，V(G)是图G的顶点集，|V(G)|是图G的顶点数，记作p=|V(G)|，E(G)是图G的边集，χ(G)是图G的顶点染色数。设S是图G的顶点集V(G)的子集，若S的生成子图G[S]是完全图，则称S是图G的一个团。显然，图G必存在最大团，用|S|表示图G最大团的顶点数。图G含有的所有最大团K|S|的公共顶点及它们在图G中的边构成的子图，记作图GS(V′,E′)，简称图GS。其中V′(GS)是V(G)的非空子集，E′(GS)是E(G)的非空子集。显然V′(GS)是图G含有的所有最大团K|S|的公共顶点集。G-V′表示从G中删去V′(GS)的所有顶点及其与V′(GS)中顶点关联的一切边后得到的图。

定义1若图G含有的所有最大团存在公共顶点，公共顶点的个数为k，则称其为第k类图。

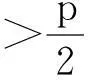
引理2[20]若|S|=p-2，则χ(G)=p-2。

引理3[20]若|S|=p-3, 则χ(G)≤p-2。

2主要结果

证明设顶点u∈V′(GS)，顶点v∈V(G-V′)，u和v不相邻。将顶点u和v删掉，必得到一个顶点数是p-2且|S|=p-4的图G′，由引理2知， χ(G′)=p-4。添上顶点u和v，就得到原来的图G，所以图G的色数必增加1，即χ(G)=p-3。

证明由图G只含有一个最大团Kp-3，故V′(GS)与V(G-V′)中必有一个顶点不相邻，否则与|S|=p-3矛盾。由定理1， χ(G)=p-3。

(1)V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻；

(2)图G是第p-4类图或第p-6类图，则χ(G)=p-3。

证明若图G是第p-4类图，V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻，且|S|=p-3，则V(G-V′)中的所有顶点互不相邻。于是V(G-V′)中的所有顶点必染同一种颜色,而V′(GS)有p-4个顶点，且是一个团,故必染p-4种颜色。因为V′(GS)中任意一个顶点和V(G-V′)中的所有顶点相邻，所以χ(G)=p-3。

若图G是第p-6类图，则图G的所有最大团Kp-3有p-6个公共顶点。因此G-V′有6个顶点，含最大团K3的图。但图G-V′中所有最大团K3没有公共顶点，否则与图G是第p-6类图矛盾。因此图G-V′中的所有最大团K3有以下4种情况。

(1)任意2个最大团K3不存在公共顶点，则图G-V′中只有2个最大团K3。不妨设最大团分别是S1和S2，则S1和S2中至少有一对顶点不相邻。将这对不相邻的顶点删掉，必得到一个顶点数是4，含有最大团K2的图G1。

由引理2知， χ(G1)=2，将删掉的顶点添上，就得到原来的图G-V′，所以顶点染色数必增加1，故χ(G-V′)=3。但V′(GS)中的任意一个顶点与V(G-V′)中的所有顶点相邻，且GS是一个顶点数p-6是的完全图，所以 χ(G)=p-3。

(2)存在2个最大团K3只有一个公共顶点，设最大团S1和S2只有一个公共顶点u，则图G-V′中必存在一个最大团S3，使u一定不是S3的顶点，否则造成所有的最大团K3有公共顶点。下面考虑由最大团S1和S2构成的含有最大团K3，顶点数是5的G1图。设图G-V′的另外一个顶点是v，v∉V(G1)，则v必是最大团S3的一个顶点，所以S3的另外2个顶点属于V(G1)。由于顶点u与图G1中的其余4个顶点相邻，所以u与v一定不相邻。将u和v删掉，必得到顶点数是4，含最大团K2的图，由引理2知，该图的色数是2。添上u和v，则顶点染色数必增加1，故χ(G-V′)=3， χ(G)=p-3。

(3)任意2个最大团K3有2个公共顶点，下面证明该情况不存在。设最大团S1的顶点是v1，v2，v3，最大团S2的顶点是v1，v2，v4，于是S1和S2构成一个顶点数是4，含最大团K3的图。设图G-V′的另外2个顶点是v5和v6，所以不存在以v5和v6为顶点的最大团K3，否则与S1和S2只有一个公共顶点，矛盾。而图G-V′中必存在以v5或v6为顶点的最大团K3，否则图G-V′中只含有最大团S1和S2，这就造成图G-V′中所有最大团K3有公共顶点，矛盾。而事实上，只要存在以v5或v6为顶点的最大团K3，则v5或v6必定与v1和v2相邻(否则存在2个最大团K3只有一个公共顶点，这与所给的情况不符)。这就造成了图G-V′中所有最大团K3存在公共顶点，这与图G-V′中所有最大团K3不存在公共顶点矛盾。故上述情况是不存在的。

(4)任意2个最大团K3或有2个公共顶点或没有公共顶点。下面证明该情况是不存在的。设最大团S1的顶点v1，v2，v3，最大团S2的顶点v4，v5，v6，则S1和S2无公共顶点。由图G-V′是顶点数为6的图，图G-V′中其余的任意一个最大团K3，则只能同时与S1和S2有两个公共顶点，矛盾。故该情况是不存在的。

综上各种情况证明，从而定理得证。

(1)V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻；

(2)图G是第p-5类图；

若图G-V′中不存在奇圈，则χ(G)=p-3；若图G-V′中存在奇圈，则χ(G)=p-2。

证明由图G是第p-5类图，|S|=p-3，则G-V′是一个顶点数为5，且含有最大团K2的图。下面分两种情况给出图G-V′的顶点染色数。由引理3知，χ(G-V′)=2或χ(G-V′)=3。

情况1图G-V′中不存在奇圈。图G-V′中有2个最大团K2不存在公共顶点。设v1，v2，v3，v4，v5是图G-V′中的5个顶点，其中v1与v2，v3与v4分别是2个最大团K2的顶点，故v1与v2相邻，v3与v4相邻，而v5最多与v1，v2或v3，v4中的一个相邻。若v5是孤立点，则有χ(G-V′)=2；若v5与v1，v2中的一个相邻，同时与v3，v4中的一个相邻，不妨设v5与v1相邻，v5与v3相邻，则v1与v3不相邻，从而v2与v4一定不相邻，否则图G-V′中存在奇圈。另设v1染颜色1，v2染颜色2，于是v3染颜色1，v4染颜色2，而v5染颜色2，故χ(G-V′)=2。由于是第p-5类图，故图GS是一个顶点数是p-5的完全图，而且图G还满足条件(1)，故χ(G)=p-3。

情况2图G-V′中存在奇圈。由图G-V′的顶点是5，则图G-V′中存在5-圈，必有χ(G-V′)=3，进而χ(G)=p-2。

综合以上情况，定理得证。

3进一步解决的问题

参考文献:

[1] 林妍, 吴瑾, 樊锁海. 图着色和标号问题的蚁群优化算法[J]. 数学的实践与认识, 2012, 42(17): 182-191.

[2] T.R.Jensen, B.Toft. Graph coloring problems[M]. New York: Wiley-Interscience, 1995.

[3] E.Malaguti, P.Toth. A survey on vertex coloring problems[J]. International Transactions in Operational Research, 2010, 17(1): 1-34.

[4] E.Salari, K.Eshghi. An ACO algorithm for the graph coloring problem[J].Int. J. Contemp. Math. Sciences, 2008, 3(6): 293-304.

[5] 朱虎, 宋恩民, 路志宏. 求解图着色问题的最大最小蚁群搜索算法[J]. 计算机仿真, 2010, 27(3): 190-192, 236.

[6] 安常胜, 冯旭霞. 几类特殊图的补倍图的点色数[J]. 天水师范学院学报, 2008, 28(2): 8-9.

[7] 谢继国, 张效贤, 徐刚. 一类6-正则循环图的点色数[J]. 甘肃高师学报, 2007, 12(5): 1-3.

[8] 达文姣, 任志国. 扇、轮和完全图的r(2)点色数[J]. 甘肃联合大学学报(自然科学版),2011, 25(2): 11-12.

[9] 任志国, 赵传成, 张忠辅, 等. 关于Sm∨Fn的边色数和点色数[J]. 兰州交通大学学报(自然科学版),2006, 25(4): 147-149.

[10]张忠辅, 王建方, 李正良. 关于图的3-色数[J]. 电子科技大学学报, 1991, 20(1): 88-91.

[11] Xu Kexiang, Song Zengmin. Coloring of some integer distance graphs[J]. Journal of Southeast University(English Edition), 2003, 19(4): 418-422.

[12] 徐灵姬, 王应前. 既不含4-圈又不含6-圈的平面图的非正常染色[J]. 中国科学: 数学, 2013, 43(1): 15-24.

[13] 卜月华, 朱旭波. 不含短圈的平面图的2-距离染色[J]. 中国科学: 数学, 2012, 42(6): 635-644.

[14] 亢莹利, 王应前. 平面图3色可染的一个充分条件[J].中国科学: 数学, 2013, 43(4): 409-421.

[15] 王维凡, 陈敏. 不含4，6，8-圈的平面图是3-可染的[J]. 中国科学A辑, 2007, 37(8): 982-992.

[16] 彩春丽, 谢德政. 平面图3-可着色的3个充分条件[J]. 河南师范大学学报(自然科学版), 2011,39(6):4-6,28.

[17] 许洋, 张雪媛. 关于平面图的3-可染色的一些结果[J]. 青岛农业大学学报(自然科学版), 2011, 28(1): 75-78.

[18] 任玉杰. 不含k3的平面图最多是-4可着色的[J]. 大学数学, 2004, 20(2): 87-88.

[19] 谢政, 戴丽. 组合图论[M]. 长沙:国防科技大学出版社, 2003: 4-5, 59.

[20] 张祥波, 魏志芹. 关于图的色数与厚度的一些新结果[J]. 高师理科学刊, 2013, 33(5): 35-37.

[21] 张祥波. 研究四色问题的意义及理论构想[J]. 数学理论与应用, 2012, 32(3): 24-28.

A Class Vertex Coloring Number of Special Graphs

ZHANG Xiang-bo

(Linpan School, Linyi 251507, China)

Abstract:If there are common vertexes in all the maximum cliques of graph, and there are k common vertexes, then we call graph is the k class graph. Hereby, this paper gives a new method to study vertex coloring of graph. According to this method, this paper studies a class vertex coloring of special graphs, and gives vertex coloring number of some graphs.

Key words:the maximum clique, vertex coloring number, first k class of graph, thickness of a graph

文章编号：1007-4260(2015)03-0011-03

中图分类号：O157.5

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.004

作者简介：张祥波，男，山东临邑人，临盘中学一级教师，研究方向为图的染色。

收稿日期：2014-09-25

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.004.html