关于不定方程x2+4n=y11(n=6,7)的求解

李 远 航

(西南大学 数学与统计学院，重庆 400715)



关于不定方程x2+4n=y11(n=6,7)的求解

李 远 航

(西南大学 数学与统计学院，重庆 400715)

摘要：利用代数数论的方法，证明了不定方程x2+4n=y11,当n=6,7时无整数解。

关键词：不定方程；整数解；代数数论

设A,B∈Z+，A无平方因子，不定方程

Ax2+B=yn,

(1)

x,y∈Z+,n∈Z,x≡1(mod2),n>1

解的讨论是代数数论中的一类重要课题。当A=1,B=1时，Ledesgue证明了式(1)无整数解。Nagell证明了当A=2,B=1,n=5时，式(1)仅有整数解(x,y)=(±11,3)。对于A=1,B=43或44,n=5,7时的情况均已讨论过，而对于A=1,B=46或47,n=11时的情况未曾讨论。因此，本文讨论此情况，给出了如下定理。

引理设M是唯一分解整环，正整数k≥2，α,β∈Z,(α,β)=1，那么若αβ=γk,γ∈M，则有α=ε1μk,β=ε2vk,μ,v∈M，其中ε1,ε2是M中的单位元素，并且ε1ε2=εk，ε为单位元素。

定理1不定方程

x2+46=y11

(2)

无整数解。

证明这里分x≡1(mod2),x≡0(mod2)两种情况进行讨论。

(1)当x≡1(mod2)时，在Z[i]中，则(2)式可写成(x+26i)(x-26i)=y11,x,y∈Z。

设d=(x+26i，x-26i)，由d|(2x,27i)=2知d只能取1,1+i，2，因x≡1(mod2)知x+23i≡1(mod2),所以d≠2；如果d=1+i，则N(1+i)|N(x+26i)，可知2|x2+46，这与x≡1(mod2)矛盾，所以d=1。由此可知x+26i=(a+bi)11,x,a,b∈Z,因而有

x=a11-55a9b2+330a7b4-462a5b6+

165a3b8-11ab10

(3)

26=b(11a10-165a8b2+462a6b4-

330a4b6+55a2b8-b10)

(4)

从式(4)可得b=±1,±2t(1≤t≤5),±26。

①当b=±1时，1±26=11(a10-15a8+42a6-30a4+5a2)，等式两边同时取模11，得

12≡0(mod11)或者3≡0(mod11)，矛盾。

②当b=±2t(1≤t≤5)，可得

±26-t=11a10-165a8b2+462a6b4-

330a4b6+55a2b8-b10

对等式两边同时取模2，则0≡a10(mod2)，知a为偶数，由x=a11-55a9b2+330a7b4-462a5b6+165a3b6-11ab6，知x也为偶数，这与x≡1(mod2)矛盾。

③当b=26时，1+260=11a10-165a8b2+462a6b4-330a4b6+55a2b8，对等式的两边同取模11，则可得2≡0(mod11)，这是不可能的。

④当b=-26时，可得

a2(11a8-165a6b2+462a4b4-330a2b6+55b8)=

260-1=32×52×7×11×13×31×41×61×151×331×1 321

因a∈Z，则a2=1,9,25或225代入验证如下

当a2=1时，b=-26，

11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10=-1 137 463 050 564 685 813≠-1；

当a2=9时，b=-26，

11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10=-1 015 422 616 648 967 869≠-1；

当a2=25时，b=-26，

11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10=-779 945 957 071 073 101≠-1；

当a2=225时，b=-26，

11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10=1 268 850 388 033 017 899≠-1；

综上，当x≡1(mod2)时，原方程无整数解。

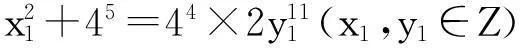
定理2不定方程

x2+47=y11

(5)

无整数解。

证明同定理1，分两种情况讨论。

(1)当x≡1(mod2)时，在Z[i]中原方程为

(x+27i)(x-27i)=y11,x,y∈Z

设d=(x+27i,x-27i)，由d|(2x,28i)=2，知道d只能是1,1+i，2。因x≡1(mod2)知x+27i≡1(mod2)，所以d≠2；如果d=1+i，则N(1+i)|N(x+27i)，即2|x2+47，与x≡1(mod2)矛盾，因此d=1。由此知x+27i=(a+bi)11,x,a,b∈Z，则可以得到

x=a11-55a9b2+330a7b4-462a5b6+

165a3b8-11ab10

(6)

27=b(11a10-165a8b2+462a6b4-330a4b6

+55a2b8-b10)

(7)

因此b=±1,±2t(1≤t≤6),±27。

①当b=±1时，1±27=11(a10-15a8+42a6-30a4+5a2)，对等式两边同时取模可得8≡0(mod11)或5≡0(mod11)，这是不可能的。

②当b=±2t，(1≤t≤6)时，

±27-t=11a10-165a8b2+462a6b4-

330a4b6+55a2b8-b10

则a必为偶数，再由x=a11-55a9b2+330a7b4-462a5b6+165a3b6-11ab6知，x也为偶数，这与x≡1(mod2)矛盾。

③当b=27时，1+240=11a10-165a8b2+462a6b4-330a4b6+55a2b8，等式两边同取模11得2≡0(mod11)，这是不可能的。

④当b=-27时，可得如下的等式：

11a10-165a8b2+462a6b4-330a4b6+55a2b8=

270-1=3×11×17×31×43×71×127×

281×86 171×122 921

由于a∈Z，所以a2=1。下面讨论这两种情况。

当a2=1，b=-27时，有

11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10=-1 176 629 904 276 659 453 941≠-1

综上，当x≡1(mod2)时，原方程无整数解。

综上讨论，不定方程x2+47=y11无整数解。

参考文献:

[1] 李中恢, 张四保. 关于不定方程x2+16=y11[J]. 海南大学学报(自然科学版),2009,3(27): 216-218.

[2] 李娜. 关于不定方程x2+4=y7的解[J]. 科学技术与工程,2011,11(23): 13-14.

[3] 高丽, 马永刚. 关于不定方程x2+42=y7[J]. 西南民族大学学报, 2008, 34(1): 27-29.

[4] 张杰. 关于不定方程x2+43=y7的解[J]. 重庆工商大学学报(自然科学版),2012, 3(29): 27-28.

[5] 冉银霞. 关于不定方程x2+44=y7[J]. 延安大学学报(自然科学版),2012, 4(31): 14-15.

[6] 冉银霞. 关于不定方程x2+46=y7[J].高师理科学刊, 2013, 4(33): 25-26.

[7] 王振, 张慧. 关于Diophantine方程x2+4n=y3[J]. 重庆工商大学学报(自然科学版),2010, 6(27):220-222.

[8] 崔保军. 关于不定方程x2+4n=y5[J]. 湖北民族学院学报(自然科学版),2011,1(29): 49-50.

[9] 潘承洞, 潘承彪. 代数数论[M]. 济南: 山东大学出版社, 2003.

On Diophantine Equation x2+4n=y11(n=6,7)

LI Yuan-hang

(Mathematics and Statistics College, Southwest University, Chongqing 400715, China)

Abstract:In the paper, using the properties of congruence and integral domain in number theory, the author has proved that the indefinite equation x2+46=y11,x,y,n∈Z has no integer solution when n is 6 and 7.

Key words:integer solution, indefinite equation, algebraic number theory

文章编号：1007-4260(2015)03-0009-02

中图分类号：O172,G642

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.003

作者简介：李远航，男，重庆江津人，西南大学数学与统计学院硕士研究生，主要从事计算数论研究。

收稿日期：2014-11-06

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.003.html