变截面桩基础的数学实验选型研究
李 飞, 孙太亮, 张砚梅
(1.中国海洋大学 海洋环境与生态教育部重点实验室,山东青岛 266100;2.中国海洋大学环境科学与工程学院,山东青岛 266100;3.青岛工学院 建筑工程学院,山东 青岛 266300;4.山东东沂勘察设计有限公司,山东 潍坊 261000)
目前变截面桩技术工程实践效果明显,国内外对变截面桩的受力性能及工作机理的研究还没有完全形成系统,在设计、计算方面虽然形成了一些地方性的规范,但是缺乏深入的理论研究和设计依据,对其荷载传递特性、沉降特性、破坏特性、最合理的盘间距、盘数量等尚不能完全定量,因此研究扩大盘位置及数量变化的变截面桩具有一定的实际意义。文献[1]基于桩的挤密效应,分析黄土地区基桩的竖向受力情况,并利用一次二阶矩法推导出基桩竖向承载力的可靠度计算公式。文献[2]利用贝叶斯统计方法,对承载力现场监测数据进行更新,并利用更新后的数据给出考虑基桩破坏的基桩承载力可靠度指标计算方法。文献[3]利用最小势能原理,考虑桩侧地基土体反力和桩周正、负摩阻力的影响,求解得到基桩的屈曲荷载与相应的计算长度,通过算例分析研究各因素对基桩竖向稳定性的影响。上述研究对桩的相关特性做了深入细致研究,针对性比较强,但针对不同变截面桩型进行分类归类,把桩基需要考虑的问题用指标体系建立起来的研究很少。本文通过模型实验,了解变截面受力过程中扩大盘桩侧阻力的受力规律及每个扩大盘在受力过程中的变化规律,分析扩大盘在不同土层中对承载力提高所起的作用,用模糊数学分析方法构建桩基在桩身强度、桩侧向阻力及地基土层等方面的指标体系,通过数学计算对变截面桩做对比分析,以验证理论推导的合理性和可操作性。
1 建立桩基础评价指标体系
通过大量实际数据的计算和现场实验可知,影响变截面桩的承载力性能很多,而且桩形受力情况也不同,通过对比分析发现,原因主要集中在桩基材料问题、桩周土体性质、桩所在土层以及桩外部环境问题等方面。关于变截面桩的承载力,主要研究方法有原位试验、室内试验、理论分析及数值模拟等,但这些方法相对独立,在桩类型选择上不能进行优化处理。层次分析法把这些类型条理化、层次化,构造一个有层次的结构模型。根据层次分析法的基本原理,可以建立变截面单桩评价指标体系[4],见表1所列。

表1 变截面桩单桩承载力主要影响因素评价指标体系
2 变截面桩单桩抗压承载力综合评价
采用遗传模糊层次分析法进行理论分析[5-6]。
(1)层次结构模型自上而下由目标层A、指标层B、准则层C组成。A为系统的总目标层,即确定建立变截面桩方案评价总指标的权重,只有一个要素。B为nb个评价指标B1,B2,…,Bn,C层为这些评价指标所隶属度nc个评价子系统C1,C2,…,Cn。层次结构模型各层中的总目标、评价子系统和评价指标系统成为评价要素,构造目标层与准则层的判断矩阵为:

矩阵B具有如下性质:①Bij>0;②Bji=1/Bij,i≠j;Bii=1,i,j=1,2,…,n。
(2)对B层和C层的要素,分别以各自的上一级层次的要素为准则进行两两比较。Bij=(2,4,6,8,1/2,1/4,1/6,1/8)表示重要性等级介于Bij=(1,3,5,7,9,1/3,1/5,1/7,1/9),这些数字根据定性分析的直觉和判断力而确定。
(3)层次各要素的单排序及其一致性检验,即确定同一层各要素对于上一层次某要素的相对重要性的排序权值,并且检验判断矩阵的一致性,先以矩阵A=(aij)nb×nb为例进行分析。设B层各要素的单排序权值为ωk,k=1,2,3,…,n,且满足ωk>0和,根据判断矩阵A的定义,理论上可得:
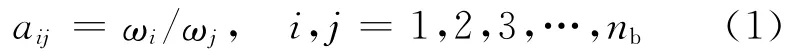
这时判断矩阵A具有如下的性质:
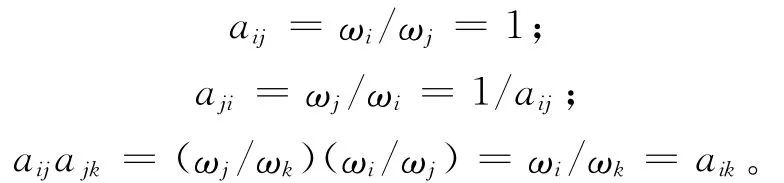
假如判断矩阵A满足(1)式,决策者就能精确地度量aij=ωi/ωj,则判断矩阵A具有完全的一致性,则有:
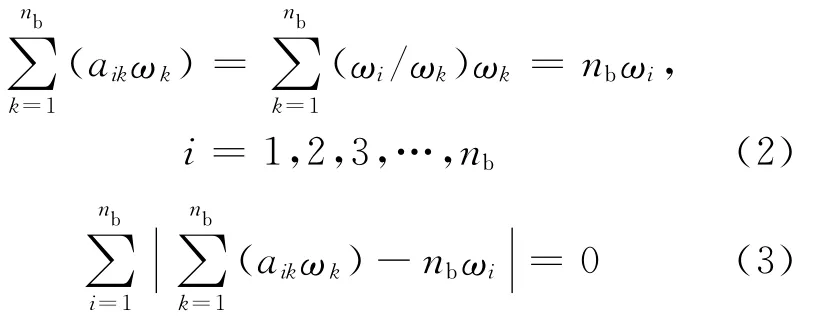
其中,||为取绝对值。由于实际系统的复杂性,以及人们主观认识上的片面性和不稳定性,对系统要素度量没有统一和确切的尺度,但是对各要素优劣认识得越清楚,一致性程度就越高,而评价各要素的优劣即为遗传模糊层次分析法所要解决的问题。
显然(3)式左侧的数值越小,判断矩阵A的一致性程度就越大,当(3)式成立时,判断矩阵A具有完全的一致性。基于此,B层各要素的单排序及其一致性检验问题可归结为:
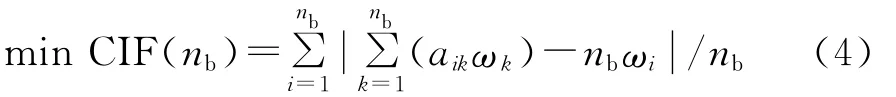
其中,ωk>0,k=1,2,3,…,nb;nb为 一致 性 指 标 函 数[7](consistency index function,CIF)。单排序权值ωk(k=1,2,3,…,nb)为优化变量。当判断矩阵A具有完全一致性时,aij=ωi/ωj成立,而(4)式取全局最小值CIF(nb)=0。(4)式是一个常规方法较难处理的非线性优化问题,而作为一种通用的全局优化问题,用自适应遗传算法(adaptive genetic algorithm,AGA)是非常好的,也是很方便的。
当CIF(nb)<0.10时,可认为判断矩阵A满足一致性,据此计算各要素单排序权重值ωk是可以接受的,否则就需要反复调整判断矩阵A,直到具有满意的一致性为止。
一致性指标函数CIF(nb)是B层总排序权重值和总排序一致性指标函数。C层各要素的总排序权值为:

总排序一致性指标函数为:

当CIFA(nc)<0.10时,认为C层总排序具有满意的一致性,据此计算各个要素的总排序权重值ωcAi是可以接受的,否则就需要通过多次调整有关判断矩阵,至要素具有符合条件的一致性为止[1-3]。
3 算例分析
3.1 变截面桩基不同方案的综合性评价
现以潍坊滨海滩涂地区桩基础使用情况为例说明桩基类型的综合遗传层次综合评价[8-9],并与室内模型实验结果做相应的对比,选择的桩形如图1所示。
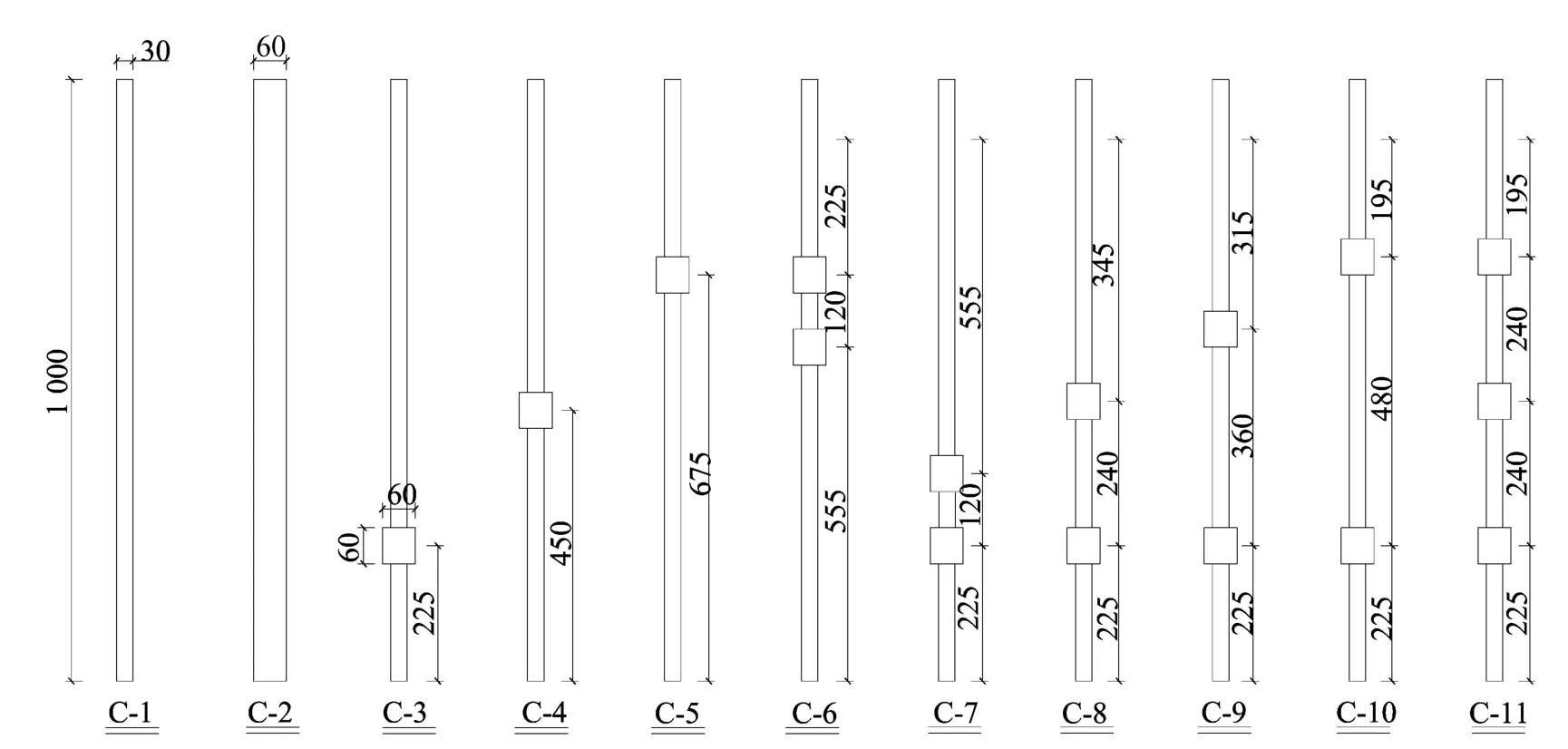
图1 多种变截面桩型
采用专家打分的方式确定各个指标的权重,准则层对于目标层的判断矩阵u为:
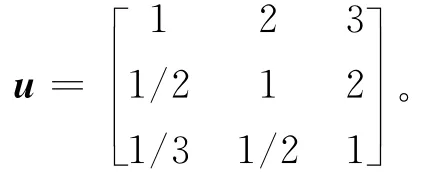
应用层次分析法,通过矩阵计算的各项指标模糊数值如下:

矩阵的一致性指标为:
CI=0.004 601 359 367 370 61,
随机一致性比率为:
CR=0.007 933 378 219 604 49。
依此类推准则层对指标层的判断矩阵u1为:

依据(1)~(6)式可求各指标的权重及一致性如下:

矩阵的一致性指标为:
CI=0.026 892 820 373 125 6,
随机一致性比率为:
CR=0.028 013 356 029 951 9。
判断矩阵u2为:

依据(1)~(6)式可求各指标的权重及一致性如下:

矩阵的一致性指标为:
CI=0.004 601 359 367 364 71,
随机一致性比率为:
CR=0.007 933 378 219 642 46,
判断矩阵u3为:

依据(1)~(6)式可求各指标权重及一致性如下:

矩阵的一致性指标为:
CI=0.004 601 359 367 342 08,
随机一致性比率为:
CR=0.007 933 378 219 685 03。
以上各判断矩阵的CI<0.01,故均满足一致性。
对于权重I和评判矩阵R[10-11],取 max-min合成运算,即用模糊型M(∧,∨)计算,可得到综合评判B=I·R,在获得了模糊综合评判集B后,即可根据最大隶属原则确定评价对象的评价结果。

桩基础选择情况的综合评价如下:

3.2 室内实验结果分析
由于篇幅原因,本文不详细介绍实验过程,仅罗列出相应的实验数据结果,以供数据对比之用。
C-7、C-10桩型的承载性能随深度的变化如图2所示。
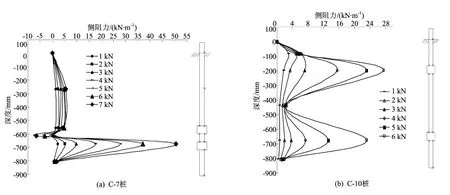
图2 不同桩承载性能随深度变化曲线
由图2可看出,两扩大盘之间直杆段的侧阻力也得到了较大程度的发挥,但由于C-10上扩大盘离桩顶比较近,桩体在试验过程中发生沉降,使得上扩大盘上部的土体发生沉降,形成局部塌陷[12-13],使得该段侧阻力没有充分发挥,从而说明C-7桩的承载力比C-10桩好。
实验过程中桩的综合能力分析如图3所示。
由图3可看出,等截面桩与变截面桩(C-2、C-1)的荷载沉降曲线基本相似;对于具有2个等间隔扩大盘的变截面桩,2个扩大盘位于上部的(C-6)桩承载力高于位于下部的(C-7)承载力,C-6曲线出现峰值是因为桩在扩大盘以上位置发生了弯曲,位于上部的扩大盘发挥了较大端阻力,因此,2个扩大盘位置应偏上设置,但注意桩身失稳;扩大盘间隔(C-7、C-8、C-9、C-10)对承载力影响不是很显著;具有3个扩大盘的变截面桩(C-11)承载力大于2个扩大盘的变截面桩承载力,但结果相差不大。
在综合评价方法中,根据最大隶属度的原则,可以推导出C-7桩(好)、C-10桩(较好)的桩基综合评级等级为“良”,这与实际情况一致,证明该综合评价方法是行之有效的。方案比选结果与室内实验得出的结论基本一致。
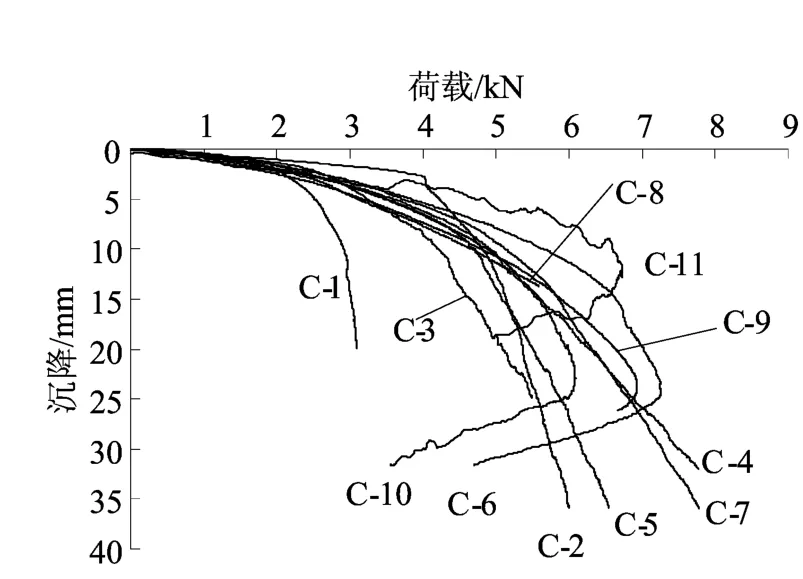
图3 等同条件下桩性能曲线
4 结 论
本文对变截面桩的受力情况进行分析,建立扩大盘在不同位置的变截面桩可靠度影响因素指标,计算相关桩的评价指标,并通过模型实验验证数学方法计算出的优秀桩型的合理性,得出以下结论:
(1)通过实验发现桩的沉降曲线变形相对缓慢,当发生荷载传递时,桩的扩大盘首先承受了主要的荷载,所以变截面桩的轴力分布与直杆桩有很大的区别,随着桩基长度增加,扩大盘以下轴力发生急剧下降。
(2)如果选择2个扩大盘的变截面桩,C-7桩较好,C-10桩次之。
(3)通过模型实验的方法可以检验桩在某假设前提下的承载性及变形性能,但实验过程过于繁琐,影响因素较多。通过数学方法可以比较快速地计算出在相应荷载条件下桩的工作性能。
[1] 胡 炜,张 磊.考虑挤密效应的基桩承载力可靠性分析[J].兰州理工大学学报,2012,38(4):122-125.
[2] 张礼兵,金菊良,吴贻名,等.确定水资源工程环境影响评价指标权重的方法[J].农业系统科学与综合研究,2002,18(3):192-195.
[3] 李 飞.互通式立体交叉方案比选系统研究[D].哈尔滨:东北林业大学,2010.
[4] 李 飞,赵倩倩,李 馨,等.基于遗传层次综合评价的绥化东枢 纽 互 通 方 案 比 选 [J].公 路 工 程,2011,36(4):119-123.
[5] 周江林.差分加速遗传算法及其在市政工程中的应用[D].合肥:合肥工业大学,2007.
[6] 杜 栋,庞庆华.现代综合评价方法与案例精选[M].北京:清华大学出版社,2005:159-162.
[7] Wu W H,Chen C Y.Simplified soil-structure interaction analysis using efficient lumped-parameter models for soil[J].Journal of the Japanese Geotechnical Society Soils and Foundations,2001,42(6):41-52.
[8] 聂春龙.边坡工程风险分析理论与应用研究[D].长沙:中南大学,2012.
[9] 孙太亮.变截面桩竖向承载特性模型试验研究[D].青岛:中国海洋大学,2011.
[10] 卢成原,孟凡丽,吴 坚,等.不同土层对支盘桩荷载传递影响的模型试验研究[J].岩石力学与工程学报,2004,23(20):3547-3551.
[11] 吴兴龙,李光茂,魏章和.DX桩单桩承载力设计分析[J].岩土工程学报,2000,22(5):581-585.
[12] 邹积君.内蒙古太仆寺旗宏观经济发展预测模型研究[D].呼和浩特:内蒙古农业大学,2003.
[13] 王小红,张晓婷,傅鹤林,等.基于遗传层次综合评价模型的局部标段路线优化及调整[J].公路交通科技:应用技术版,2013(4):48-51.

