基于增强邻域结构方向信息的图像去噪算法
陈强云, 郭铭铭, 窦建华
(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009;2.合肥工业大学 教务部,安徽 合肥 230009)
0 引 言
文献[1-4]利用图像中存在大量的自相似块这些冗余信息提出了非局部均值(NLM)算法,通过计算待去噪像素点邻域与搜索区域的像素点邻域的相似度来确定滤波的权值。非局部均值的核心问题之一是如何准确地度量图像块间的相似性[5-6],传统的 NLM 算法使用图像的灰度信息,仅考虑图像的局部几何结构,在计算邻域间相似性时不能很好地捕获图像块之间的结构方向信息,从而影响图像去噪效果[7-8]。
针对这一不足,本文利用局部结构方向信息相似度(LSOS)算法与高斯加权的欧式距离乘积作为相似度,能够更加合理地描述邻域间的相似性度量,以达到在滤波时加入结构方向信息的目的,提出了利用LSOS改进的非局部均值去噪算法(NLM-LSOS)。
实验证明,该算法具有很好去噪效果的同时还能够保留图像的边缘结构信息,获得良好的方法噪声。
1 非局部均值去噪算法
对于加性噪声,含噪图像v(i)可以建模为无噪声图像u(i)与高斯白噪声n(i)的加权和,即
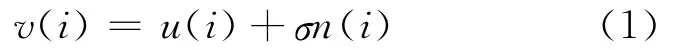
图像去噪的目的就是从含噪声图像中获取无噪图像。非局部均值计算一个全图所有像素的加权平均作为去噪后该点像素的估计值,即

其中,权值w(i,j)取决于像素i和像素j之间的相似性,并满足0≤w(i,j)≤1和。像素i和像素j之间的相似性由其灰度值向量n和m的相似性决定,n是像素i为中心的固定大小的方形邻域。
邻域灰度值向量的相似性由高斯加权的欧式距离来确定,即
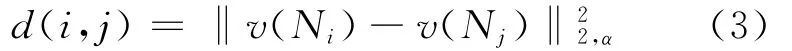
其中,α>0为高斯的标准差。
邻域灰度值向量越相似,则相应像素点在加权平均中的权值越大,定义权重为:
数h控制指数函数的衰减速度。
2 信息相似度(LSOS)算法
2.1 非局部均值邻域相似性度量
传统的非局部均值算法在相似度计算时使用各向同向邻域,不能反映图像块的方向信息,在计算相似性时不能很好地捕获图像块之间结构的相似性,尤其在处理方向性纹理性较强的图像时,不能有效地捕获纹理的方向信息。
图1所示为方向相似性对比图,图中数字代表该点的像素值,空白点表示该点像素值为0。用传统的非局部均值算法来度量相似图像块时,图像块2和图像块3对于图像块1来说具有相同的相似性,但是从图像块的结构来看图像块2包含了和图像块1相似的方向信息,才是图像块1真正意义上的相似块。对于传统非局部均值来说,由于图像块2和图像块3具有相同的相似度,进而在非局部均值加权平均中具有相同的权值,没有反应图像块间的方向信息,不能使真正相似的图像块取得更大的权值,影响在结构信息复杂区域去噪效果。

图1 方向相似性对比图
2.2 邻域方向结构信息提取过程
为了解决图像块误匹配的缺陷,找到真正意义上相似的图像块,提高结构复杂区域的去噪效果,引入了局部结构方向相似度(LSOS)来度量图像块间的相似度[9-12]。为挖掘图像中的结构信息,利用图像中邻近像素点的相关性对图像边缘、纹理等结构分布的影响,提出了基于局部结构方向相似度的图像质量评价方法(structural orientaion information,SOI)。
图像局部方向信息提取是对于图像中任意一点像素(i,j),令len为点(i,j)邻域的1/2,点(i,j)邻域为:
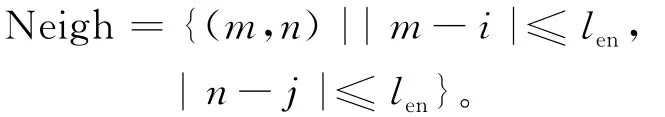
让一条角度为θ的直线L(θ)过点(i,j),将邻域 Neigh分为s1、s2,则点(i,j)的方向信息为:
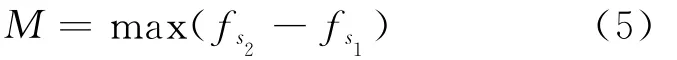
当M取最大值时,则方向信息为对应的角θ方向。其中0°≤θ≤180°,点(i,j)像素用xij表示,当取定角θ时的内积模板Qθ,len=1时,按逆时针取0°、45°、90°、135°、180°、225°、270°、315°8 个方向所对应的8个模板,如图2所示。
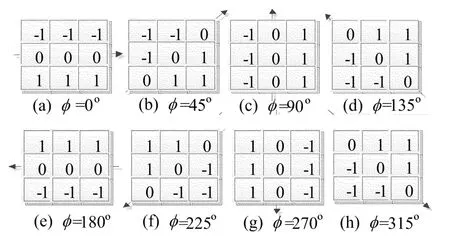
图2 邻域划分模板示意图
通过(5)式计算像素点邻域内灰度分布的差异,从而得到像素点(i,j)灰度的方向信息,当在该区域内有方向角为θ的方向线过像素点(i,j)时,同时方向角为θ对应的模板能使(5)式取得最大值,其值越大,说明方向线两边像素灰度分布差异越大,所以(5)式能够有效地反映像素点(i,j)所在线的方向信息。结构方向信息算法是发现SSIM算法还没有充分利用图像中的结构信息,并在此基础上对图像的结构方向信息进一步挖掘,(5)式变为:

其中,μi和σi分别表示以像素i为中心的方形邻域的灰度均值和方差;σij表示邻域间的灰度协方差;N为邻域或邻域所包含的所有像素点个数;S为邻域间有相同方向信息的像素点个数。
传统的非局部均值算法,用高斯加权的欧式距离来定义相似性,越接近0,则2个小块相似性越好。LSOS的取值范围为[-1,1],当LSOS绝对值越大时,说明2个小块的相似性越好,为了和高斯加权欧式距离一致,定义邻域结构方向相似参数为:

其中,LS(i,j)取值为[0,1]。当 LS(i,j)取值越小,2个小块相似性越高,即与高斯加权的欧式距离有相同的单调性。将该结构方向相似度参数与高斯加权的欧式距离相乘,作为对邻域块相似性度量的改进,具体计算公式为:

其中,E[LS(i,j)]为针对像素i的归一化常数,其值为:
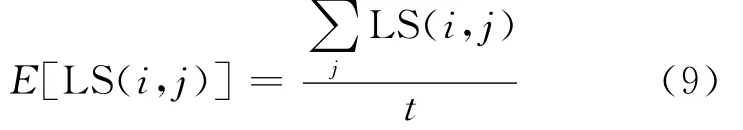
其中,t为j的个数。
2.3 改进后的非局部均值算法
经上述改进后,2个图像块的相似性为:
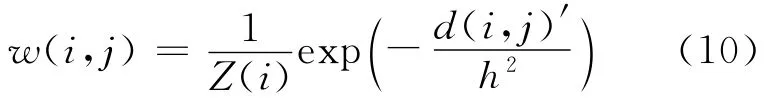
改进后的算法流程如图3所示。
这样将结构方向信息用到图像去噪滤波器中,使滤波后的图像包含尽量少的结构方向信息,得到很好的方法噪声。

图3 改进后算法流程图
3 实验结果分析
3.1 图像去噪效果分析
采 用 cameramen、house、rice 3 幅 大 小 为256×256的灰度图,分别加入噪声方差为10、20、30、50的高斯噪声,实验结果如图4~图6所示。

图4 α=10时,改进前、后非局部均值去噪所得结果
图4a中人物右手手指的边缘结构信息已经变得非常的模糊不清,而图4b中的人物右手手指可以清晰地辨认。改进的非局部均值算法在去除噪声的同时能够很好地保留原始图像的方向结构信息,去除的噪声也更加接近高斯分布。实验过程中不断增大噪声,结果对比如图5、图6所示。


图5 α=20时,改进前、后非局部均值去噪所得结果
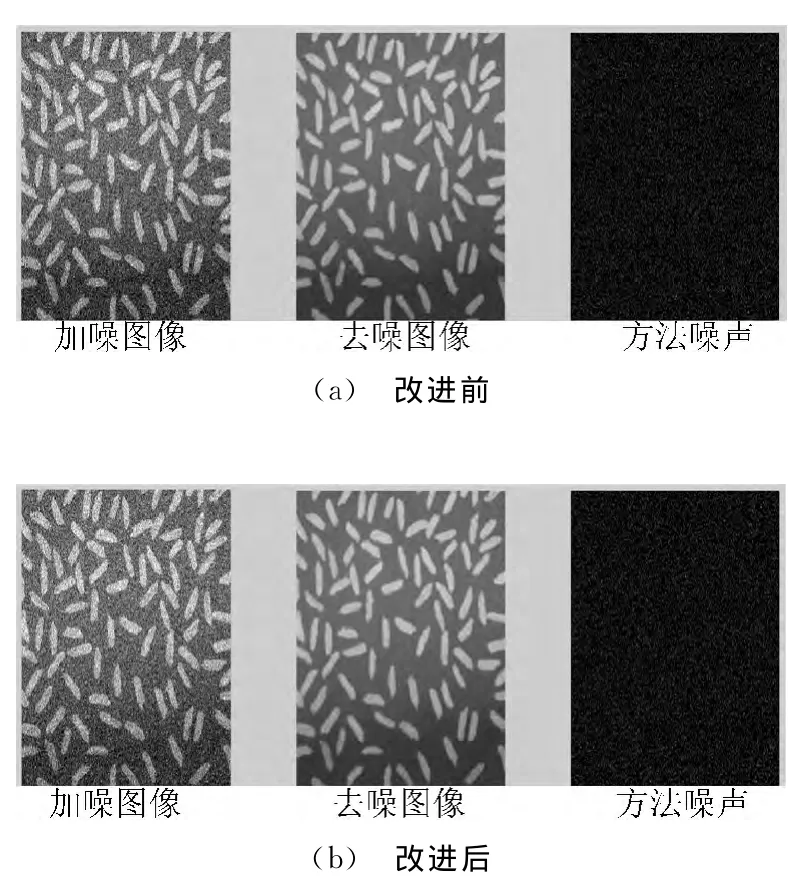
图6 α=30时,改进前、后非局部均值去噪所得结果
从图4~图6可看出,改进后的非局部均值算法的去噪效果要优于原始的非局部均值算法,图像整体上在细节边缘部分能够很好地体现,得到的方法噪声也接近之前所添加的噪声。
在噪声较大的情况下,改进后的算法也能取得较好的去噪效果,如图7所示。

图7 α=50时,改进非局部均值去噪所得结果
图8所示为加入高斯噪声和椒盐噪声的混合噪声去噪效果图。
从图8中可看出,改进后算法对椒盐噪声去噪效果不是太理想。由于椒盐噪声对区域像素点的像素值影响较大,使像素点估计值出现一定的偏差。

3.2 峰值信噪比对比分析
对2种方法得到的实验图像,计算其峰值信噪比,结果见表1所列。由表1可知,改进的非局部均值算法得到的峰值信噪比要高于传统的非局部均值算法。每幅图及其对应的峰值信噪比取10次平均值。

表1 不同程度噪声下所得信噪比
4 结束语
本文在传统的非局部均值算法的基础上提出了一种增强邻域结构方向信息的非局部均值图像去噪算法,研究如何充分利用图像本身的几何机构信息和方向结构信息来达到去除噪声的目的,正确提取图像中的结构方向信息。本文改进的算法将图像中的结构方向信息和几何结构信息有效地结合起来,在图像去噪中得到了很好体现。其算法在去除图像噪声的同时能够很好地保留图像的结构信息,使去噪后的图像结构更加清晰,接近原始不含噪声图像,提高去噪后图像的信噪比,得到很好的方法噪声。由于在去噪时增加了图像的结构信息,从而加大了算法的复杂度,延长了去噪所需时间,今后可继续挖掘图像本身中的更多其他方面冗余信息,使其能在具有混合噪声的图像中取得更好的去噪效果。
[1] Buades A,Coll B,Morel J M.A review of image denoising algorithms,with a new one [J].SIAM Journal on Multiscale Modeling and Simulation,2006,4(2):490-530.
[2] Mahmoudi M,Sapio G.Fast image and video denoising via non-local means of similar neighborhoods[J].IEEE Signal Process Lett,2005,12:839-842.
[3] Deledalle C,Salmon J.Image denoising with patch based PCA:local versus global[C]//BMVC,Britain,2011:121-130.
[4] Weng F,Kelong Z.A non-local bilateral filter for image denoising[C]//2010International Conference on Apperceiving Computing and Intelligence Analysis,2010:235-257.
[5] Fan H,Yu Y,Peng Q.Robust feature-preserving mesh denoising based on consistent subneighborhoods[J].IEEE Transaction on Visualizaton and Computer Graphics,2010,16(2):312-324.
[6] Grewening S,Zimmer S,Weickert J.Rotationally invariant similarity measures for nonlocal inage denoising[J].Journal of Visual Communication and Image Representation,2011,
[7] 薛年喜.MATLAB在数字信号处理中的应用[M].北京:清华大学出版社,2003:33-45.
[8] 冈萨雷斯.数字图像处理[M].第2版.北京:电子工业出版社,2003:67-89.
[9] Wang Z,Bovik A C,Sheckh H R,et al.Image equality assessment from error visibiliy to structural similarity [J].IEEE Transaction on Image Processing,2004,13(4):600-612.
[10] Jiang G,Huang D J,Wang X,et al.Overview on image quality assessment methods[J].Journnal of Electronics &Information Technology,2010,32(7):219-226.
[11] 沙 浩,江 平.基于分类准则的非下采样Contourlet变换域图像去噪[J].合肥工业大学学报:自然科学版,2013,36(7):892-896.
[12] Xiong B,Yin Z P.A universal denoising framework with a new impulse detector and nonlocal means[J].IEEE Transaction on Image Processing,2012,21 (4):1663-1675.

