利用偏振分析的雾天图像复原
方 帅, 夏秀山, 赵育坤, 于 磊
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
0 引 言
雾天图像由于受到大气粒子的散射和吸收作用会发生对比度丢失、颜色失真等退化现象,这些退化严重影响图像的高级处理。当前较好的去雾算法有2类:单幅图像去雾算法[1-3]和基于偏振的去雾算法[4-8]。单幅图像去雾算法能够取得较好的结果,但是这类方法通常有较大的局限性,如文献[2]中需要图像满足暗原色先验假设,而这一假设在有些情况下不成立;基于偏振的方法需要较少的假设,因为这类算法至少要采集2幅偏振图像,故具有更多的信息。此外,基于偏振的方法在去雾的同时能够提供场景的偏振信息,尤其是场景目标的偏振信息,因此在目标识别[9-10]、场景分割[11]和材质分类[12-13]等领域有着重要的应用。
雾天场景入射到成像设备的光是由目标反射光和周围散射到成像路径上大气光合成的。文献[4-5]假定只有大气光具有偏振效应,忽略目标反射光的偏振效应,而文献[6]中又指出这一假设在镜面(如水面)等区域并不成立,因此通过检测图像中的镜面区域修正了错误结果,然而仅仅在镜面区域的错误得到修正,图像其他区域去雾效果并没有改善。事实上图像偏振效应是由目标反射光的偏振效应和大气散射光的偏振效应共同作用的结果。大气散射光的偏振效应随着气溶胶粒子大小、成像距离、太阳位置等不同而不同;目标反射光的偏振效应不仅与入射光有关,还与目标本身的导电性、表面特性等物理化学属性有关,所以不同的物体具有不同的偏振特性。仅考虑大气光偏振效应具有较大的局限性,会导致此类算法在水面等目标反射光偏振效应较明显的区域无法工作,大大限制了算法的适用范围。
针对传统的偏振去雾算法存在的问题,本文提出了同时考虑目标反射光和大气散射光偏振效应的偏振去雾模型。基于新的模型,给出了有效的去雾算法,取得了较好的去雾结果,拓展了偏振去雾算法的适用范围,还得到了具有重要应用价值的目标偏振度图和传输图。
1 光学模型
1.1 偏振成像模型
当使用斯托克斯向量表示光的偏振态时[14],光的线偏振度(DoLP)p和偏振角(AOP)α定义为:
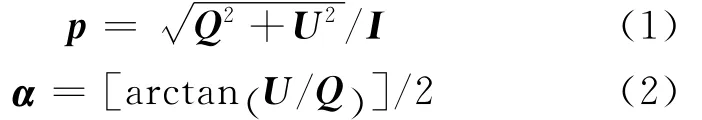
其中,I、Q和U为斯托克斯向量的前3个分量。
光通过线偏振片后强度会发生改变。假设偏振片和选定的参考方向夹角为θ,则通过偏振片后图像(x,y)处的光强S(x,y,θ)满足的规律[15-16]如下:

通过采集3幅不同角度的偏振图像带入(3)式,得到3个独立的方程构成方程组,可解得I、Q和U。
1.2 雾天偏振成像模型
雾天由于大气粒子的散射作用,入射到成像路径上的光是大气散射光和目标反射光的合成,且大气光、目标反射光以及合成后的光均是部分偏振光[2,4-5,17-19]。
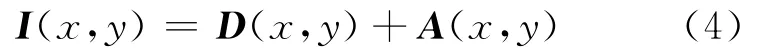
其中,I(x,y)为图像点(x,y)处的光强;D(x,y)为直接透射光,描述了场景目标反射光的衰减过程;A(x,y)为大气光,描述了成像路径上周围杂散光的累积过程。D(x,y)和A(x,y)的表达式分别为:

其中,J为场景目标本身亮度;A∞为无穷远处大气光强度;t的表达式为:

其中,β为大气的散射系数。由于本文假设大气是均匀介质,故β是全局量。(7)式指出t取决于场景深度,故又称深度图或传输图。
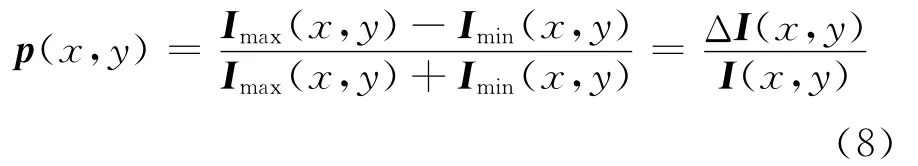
根据偏振度的定义[4,6,16],(1)式又可等价地表示为:其中,Imax(x,y)和Imin(x,y)分别为通过旋转偏振片在点(x,y)处能取到的最大和最小光强。定义ΔI=Imax-Imin表示偏振差分(PD)图,I=Imax+Imin表示偏振和图像[16]。
同理,可得到直接传输项D(x,y)和大气光项A(x,y)的偏振度定义为:
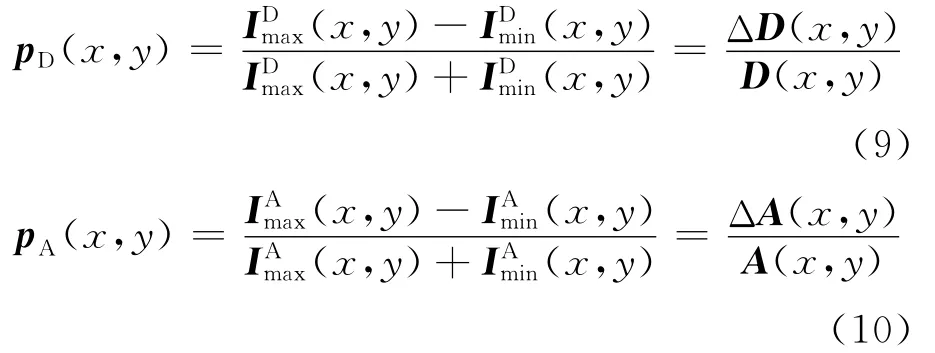
结合(4)式、(9)式和(10)式,可得雾天偏振成像模型如下:

2 去雾算法
2.1 雾天图像复原
由(4)式、(6)式、(8)式和(11)式可得传输图t的表达式为:

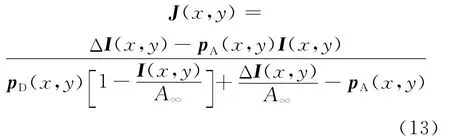
结合(4)式、(5)式、(6)式和(12)式可得场景辐射亮度J的表达式为:由(13)式可知要想恢复场景亮度J,需要估计如下参数:偏振差分图ΔI、无穷远处大气光强度A∞、大气光偏振度pA和目标偏振度pD。偏振差分图ΔI可通过偏振图像Imax和Imin求得。
2.2 估计偏振差分图ΔI
结合(1)~(3)式可得:
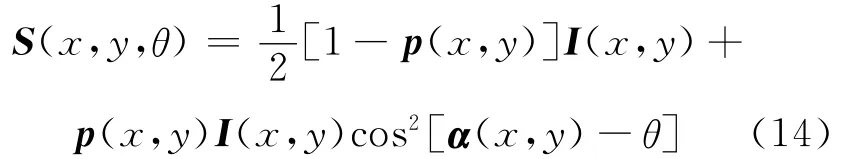
通过旋转线偏振片,拍摄3幅不同角度的偏振图像,可以求得p、α和I。由(14)式可知,当θ=α时,观测的图像强度达到最大值(此时图像记为Imax);当θ=α±π/2时,观测的图像强度达到最小值(此时图像记为Imin)。由于场景中不同物体的物理化学性质等不一样导致其偏振特性也不一样,因此无法直接旋转偏振片拍摄到Imax和Imin,但是通过(15)式可合成Imax和Imin图像,即

则偏振差分图可通过ΔI=Imax-Imin求得。
2.3 估计大气散射光偏振度pA和A∞
由于本文假定大气是均匀的,因此可认为pA和A∞是全局量。本文采用文献[4-6]的方法,通过选取天空区域来估计这2个参数,计算公式为:

其中,|Ω|为选取的天空区域内像素的个数。
2.4 去相关法估计pD和t
由于目标都有一定的大小,故本文假定在一个较小的区域ω内pD是相同的。传输图t由场景深度和大气衰减系数共同决定,而场景亮度J由场景所在处目标本身决定,通常与光照条件和目标材质等有关,故假设t和J在ω内不相关[3,16],用公式表达为:
Covω[t(x,y),J-1(x,y)]=0, (x,y)∈ω。
考虑到实际图像中都存在一定的噪声,故通过求解最优化问题得到pD,即
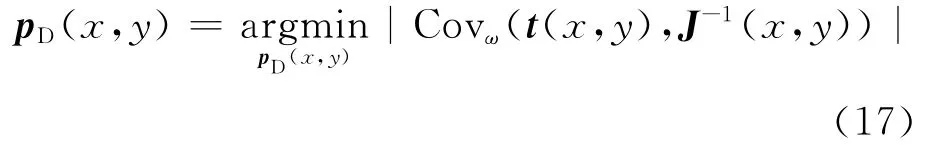
其中,Covω为在局部块ω内求协方差。将(12)式和(13)式带入(17)式可得:

由于包含图像边缘的区域ω内目标偏振度不相等,因此实际中使用加权协方差的形式来求解,区域ω内权值由区域中心像素和周围像素的相似性确定,再通过dE2(pD)/dpD=0来求解(18)式的最优化问题。估计出目标偏振度图pD后带入 (12)式即可求得传输图t。
2.5 修正目标偏振度图pD和传输图t
实验中发现,由于噪声等影响,通过2.4节算法求得的传输图仍然会出现估计错误点。为了解决这个问题,本文利用引导滤波[20]对估计的传输图进行修正。引导滤波能在平滑图像的同时保留图像的边缘信息,因此利用引导滤波可以修正t图错误点,同时保持图像的边缘和结构信息。为表述方便,记传输图为向量形式,并定义滤波前后的传输图分别为t和,则点i处的滤波修正可表示为:

其中,μk和σk分别为窗口ωk内像素的均值和方差;Ii和Ij分别为输入图像I在i和j点的像素值;ε为归一化参数,通常取很小的值。
对图像t中的每一点通过(19)式的滤波操作即可获得修正后的传输图。将修正后的代入(12)式可得修正的目标偏振度图D。
3 实验结果
3.1 算法框架
本文算法的流程主要分为3步:
(1)合成偏振图像Imax和Imin,估计偏振差分图ΔI。
(2)估计大气光参数,利用去相关方法估计目标偏振度并求得传输图。
(3)利用引导滤波修正传输图中存在的错误点,并利用修正后的传输图带入(12)式得到修正的目标偏振度图,最后恢复出场景亮度信息。
3.2 本文算法结果
几组本文算法的去雾结果如图1所示。图1中前3列表示输入的3幅不同角度的偏振图像,最后一列是本文算法的去雾结果。可以发现,通过本文算法复原的雾天图像对比度显著提升,图像细节更加丰富。

图1 本文实验结果
3.3 本文算法与传统算法的对比
传统的偏振去雾算法仅考虑大气散射光的偏振效应,而本文去雾算法同时考虑大气散射光和目标反射光的偏振,因此本文算法可获得更好的实验结果。分析可知,如果只考虑大气散射光的偏振,则表达场景亮度J的(13)式可改写为:
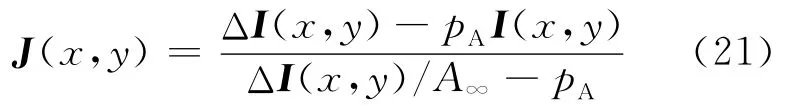
本文算法和仅考虑大气光偏振算法的对比实验结果如图2所示。

图2 本文算法和仅考虑大气光偏振算法的对比结果
图2a、图2b和图2c是输入的3幅偏振图像;图2d是合成的最大光强图Imax;图2e是合成的最小光强图Imin;图2f是偏振差分图;图2g是估计的粗糙的目标偏振度图pD;图2h是估计的粗糙的传输图t;图2i是修正后的传输图;图2j是修正后的目标偏振度图D,可以看出不同目标的偏振度明显不同,将其与传统强度图结合可以解决很多仅使用强度图无法解决的问题;图2k是仅考虑大气光偏振时的去雾结果;图2l是本文算法的去雾结果;图2m是图2k中矩形区域的放大结果;图2n是图2l中矩形区域的放大结果。从实验结果可以看出本文算法与仅考虑大气光偏振的算法相比,复原结果具有更高的对比度、更清晰的图像细节和更低的噪声。
本文算法与仅考虑大气光偏振的算法相比具有更低的噪声,这一结果也可通过对比(13)式和(21)式得到。观察 (21)式可知ΔI/A∞通常是一个较小的值,如果此时大气光偏振度pA也是一个相对较小的值,则 (21)式中的分母将过小,这导致复原的场景亮度噪声被过度放大。而本文的复原公式(13)式与 (21)式相比由于多出来一项pD(1 -I/A∞),因此具有更大的分母值。只有当目标偏振度pD和大气偏振度pA几乎相等的时候,本文算法噪声才会明显。因此通常情况下本文算法复原后的图像具有相对较低的噪声。
文献[4-5]中输入的图像是2幅正交角度的偏振图像,这2幅偏振图像分别称为最佳偏振图像和最差偏振图像。文献[4-5]的算法中忽略目标反射光的偏振,而仅考虑大气散射光的偏振。由于文献[4-5]未提供算法源码,故为了对比,本文使用文献[4-5]中提供的最佳和最差偏振图像替代本文算法中的Imax和Imin图像,作为本文算法的输入。
本文算法和文献[4]算法的对比实验结果如图3所示。
图3a和图3d是2幅输入图像,图3b和图3e使用的是文献[4]中的实验结果,图3c和图3f是本文的去雾结果。由图3可以看出,在水面区域,本文结果要明显优于文献[4]的结果,这是由于文献[4]中假设目标反射光偏振度为0,而这一假设在水面等区域不成立,因为水体等通常具有较大的偏振度。尽管在文献[6]中通过对水面区域单独处理而部分解决了这个问题,但是本文同时考虑大气和目标偏振度,从模型上解决了这个问题。因此本文算法具有更广泛的适用场景,且不需要额外的处理步骤。

图3 与文献[4]的去雾结果对比
3.4 去雾结果的定量评价
本文采用无参考的自然图像质量评价算法(NIQE)[20]来 定 量 地 评 价 去 雾 结 果 的 好 坏。NIQE算法是通过采集所有对图像质量敏感的特征,并把这些特征拟合成一个多元高斯(MVG)模型。这些特征通过自然场景统计(NSS)模型即归一化的局部亮度系数得到,文献[21]详细分析了选取的36个特征,指出自然图像归一化后的亮度系数近似地满足类高斯分布,而发生失真(不针对任何特定的失真类型)的图像不满足这种分布。因此,对于一幅给定的测试图像的质量可以简单地表示为测试图像的MVG模型和自然图像MVG模型之间的距离。自然图像的MVG模型是通过统计图像库中大量的自然图像得到的。因此求取测试图像质量的公式可表述为:


其中,ν1、ν2和Σ1、Σ2分别为自然图像和退化图像MVG模型中的均值向量和方差矩阵。
NIQE算法的评价结果见表1所列。表1中的值代表测试图像和自然图像的MVG模型间的距离,故值越小表示测试图像越接近自然图像,即值越小图像质量越高。结果表明与传统的偏振去雾算法比较,本文算法的去雾结果具有更高的视觉质量。
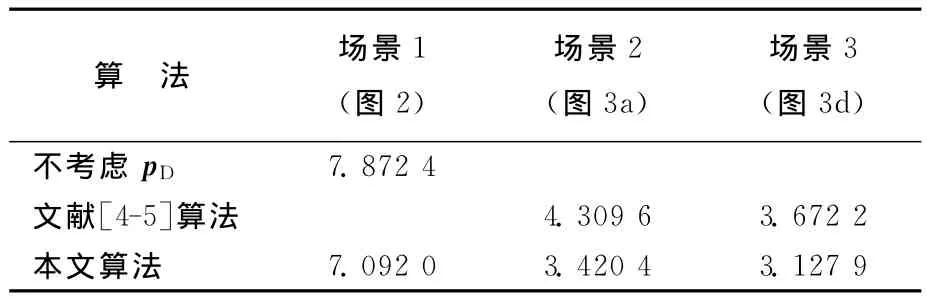
表1 去雾结果图的视觉质量对比
4 结束语
本文算法和传统的偏振去雾算法主要不同点是同时考虑大气散射光和目标反射光的偏振效应,因此在复原雾天场景真实信息的同时,可提供反映目标偏振特性的目标反射光偏振度和最优偏振差分图,这些都是传统偏振去雾算法无法提供的。实验部分给出了本文算法与相关算法结果的定量评价指标,定量地说明了本文算法具有更好的视觉质量。此外本文算法求得的目标偏振度图pD在目标识别、图像分割等领域有着重要的应用价值。
[1] 孙洪伟,朱志超,于 磊,等.一种提高雾天图像清晰度的方法[J].合肥工业大学学报:自然科学版,2011,34(1):83-86.
[2] He K M,Sun J,Tang X O.Single image haze removal using dark channel prior[J].IEEE Transactions on Pattern Analysis and Machine Prior,2009,33(12):2341-2353.
[3] Fattal R.Single image dehazing[C]//Proc ACM SIGGRAPH,2008:1-9.
[4] Schechner Y Y,Narasimhan S G,Nayar S K.Instant dehazing of images using polarization[C]//Proc CVPR,Vol 1,2001:325-332.
[5] Schechner Y Y,Narasimhan S G,Nayar S K.Polarizationbased vision through haze[J].Applied Optics,2003,42(3):511-525.
[6] Namer E,Schechner Y Y.Advanced visibility improvement based on polarization filtered images[M]//Polarization Sci-
ence and Remote SensingⅡ,2005:36-45.
[7] Namer E,Shwartz S,Schechner Y Y.Skyless polarimetric calibration and visibility enhancement[J].Optics Express,2009,17(2):472-493.
[8] Shwartz S,Namer E,Schechner Y Y.Blind haze separation[C]//Proceedings of IEEE Computer Society Conferece on CVPR,2006:1984-1991.
[9] Saito M,Sato Y,Ikeuchi K et al.Measurement of surface rientations of transparent objects using polarization in highlight[J].JOSA A,1999,16(9):2286-2293.
[10] Chen H,Wolff L B.Polarization phase-based method for material classification and object recognition in computer vision[C]//Proceedings of SPIE 2599on Three-Dimensional and Unconventional Imaging for Industrial Inspection and Metrology,1996:54-63.
[11] Lin S S,Yemelyanov K M,Pugh E N,et al.Separation and contrast enhancement of overlapping cast shadow components using polarization[J].Optics Express,2006,14(6):7099-7108.
[12] Wolff L B.Polarization-based material classification from specular reflection[J].IEEE Transactions on Pattern A-nalysis and Machine Intelligence,1990,12 (11):1059-1071.
[13] Tominaga S,Kimachi A.Polarization imaging for material classification[J].Optical Engineering,2008,47(12):760.
[14] Chipman R A.Polarimetry[J].Handbook of Optics,1995,2(2):1-28.
[15] Hyde M W,Cain S C,Schmidt J D.Material classification of an unknown object using turbulence-degraded polarimetric imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2010,49(1):264-276.
[16] Yemelyanov K M,Lin S S,Pugh E N,et al.Adaptive algorithm for two and 3-channel polarization sensing under various polarization statistics with nonuniform distributions[J].Applied Optics,2006,45(22):5504-5520.
[17] Middleton W E K.Vision through the atmosphere[M]//Geophysik II/Geophysics II.Berlin:Springer,1957:254-287.
[18] Narasimhan S G,Nayar S K.Vision and the atmosphere[J].Internation Journal of Computer Vision,2002,48(3):233-254.
[19] He K M,Sun J,Tang X O.Guided image filtering[C]//Proceeding of 11th European Conference on Computer Vision,2010:1-4.
[20] Mittal A,Soundararajan R,Bovik A C.Making a“completely blind”image quality analyzer[J].IEEE on Signal Processing Letters,2013,20(3):209-212.
[21] Mittal A,Moorthy A K,Bovik A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactons on Image Processing,2012,21(12):4695-4708.

