基于AKPSO算法的加速度计快速标定方法*

戴邵武， 王克红， 钱俭学

(1.海军航空工程学院 控制工程系，山东 烟台 264001；2.92349部队，山东 淄博 255178)

基于AKPSO算法的加速度计快速标定方法*

戴邵武1， 王克红1， 钱俭学2

(1.海军航空工程学院 控制工程系，山东 烟台 264001；2.92349部队，山东 淄博 255178)

针对粒子群优化(PSO)算法在加速度计标定优化后期出现的早熟、陷入局部最优的不足，以及KalmanPSO(KPSO)算法在设计与应用过程中存在的缺陷，提出了基于自适应Kalman滤波的改进PSO(AKPSO)算法，并将其成功应用于加速度计快速标定。利用粒子群状态空间Markov链模型，建立了粒子群系统状态方程和观测方程；采用指数加权的自适应衰减记忆Kalman滤波来对粒子的位置进行估计。加速度计标定仿真结果表明：所提出的算法在收敛速度、收敛精度方面都要优于PSO，KPSO算法，有效地提高了加速度计的标定精度。

加速度计标定； 自适应Kalman粒子群优化； Markov链模型

0 引 言

惯性导航是一种抗干扰能力强、隐蔽性好不依赖于任何外部信息的自主导航系统，在航空、航天、航海和许多民用领域都得到了广泛的应用。然而惯性导航精度随时间增长而不断下降的缺点严重制约了其导航精度的提高。惯导系统误差的标定与补偿，是提高惯导系统精度十分有效的方法。对此，荷兰学者Lötters J C在1998年提出了基于模观测的加速度计标定方法[1]，基本原理是三轴的加速度计测量值的模等于重力加速度的模，以此为依据,列写待标定参数的非线性方程组，这样加速度计的标定就转化为非线性方程组的优化求解问题。针对传统非线性方程组求解方法[2～4]存在的不足，有学者将粒子群优化(particle swarm optimization,PSO)算法[5]引入到加速度计的标定中，证明了基于PSO算法的加速度计标定方法具有可行性、有效性，与传统牛顿迭代标定方法相比，更加具有优越性。

然而，在标定优化后期，PSO算法出现了早熟、标定值陷入局部最优，导致优化结果与理想结果之间存在一定差异。随着对基本PSO算法研究的不断深入，一些学者[6,7]将Kalman滤波原理引入到PSO算法，提出了KPSO(Kal-man PSO)算法，证明了KPSO算法在全局搜索能力和局部搜索能力方面都强于基本PSO算法，并将其成功应用于数据分类。但文献[6]只报道了Kalman滤波对基本PSO算法搜索能力的提升，对滤波器的设计没有进行深入的探讨，对滤波器应用过程中存在的缺陷没有分析；粒子运动的建模也只采用了线性模型，而实际的粒子运动是非常复杂的随机运动，滤波模型参数难以适应实际系统，容易导致滤波发散。

针对上述问题，本文提出了自适应Kalman滤波改进的PSO算法(adaptive Kalman PSO,AKPSO)，并将其应用于加速度计的快速标定中，仿真结果表明:AKPSO算法能够有效地提高加速度计的标定优化精度。

1 加速度计标定原理

1.1 加速度计输出模型

在只考虑零阶和一阶参数时，加速度计单位时间脉冲输出模型[8]为

=Ka·fb+Da+na,

(1)

式中Ka为加速度计的脉冲当量矩阵，Na为单位时间加速度计输出脉冲,pulse;fb为比力矢量在b系的表示，Da为加速度计常值零偏,m/s2;na为加速度计测量噪声。

根据公式(1)表示的加速度计输入输出关系，可以从加速度计脉冲输出得到比力测量结果

=KANa-f0-δa.

(2)

1.2 模观测标定原理

静态条件下，加速度计的测量满足

(3)

(4)

公式(4)表明，静态条件下，无论惯测组合处于什么姿态，加速度的模都是已知的。

将加速度计标定参数模型(2)代入式(4)得

|fb|=|KANa-f0-δa|=g.

(5)

两边平方，整理得

g2=|fb|2=(KANa-f0-δa)T(KANa-f0-δa).

(6)

式(6)是关于加速度计待标定参数的非线性方程，多个位置的观测可以组成非线性方程组，求解非线性方程组就可得到标定参数。针对传统非线性方程组求解方法的不足，将PSO方法引入到非线性方程组的求解之中，构造目标函数

(7)

这里，θa为待标定参数θa=[KAf0]，J为标定时静态测试的位置数。这样，就将非线性方程组的求解问题转化为一个全局优化问题，通过最小化目标函数即可得到待标定参数。

2 AKPSO算法

2.1PSO算法描述

PSO算法是Kennedy和Eberhart提出的一种基于种群的随机优化算法，源于对鸟群觅食等社会行为的模拟。与其它进化算法类似，粒子群算法也是通过个体间的协作与竞争，实现复杂空间中最优解的搜索。算法中，每个优化问题的解被看作搜索空间的一个“粒子”，粒子在解空间运动，由一个速度决定其飞行方向和距离。每一次迭代过程中，粒子跟踪两个“极值”来更新自己的速度和位置：一个是粒子本身找到的最优解，另一个是整个种群的全局最优解，粒子速度和位置更新方程如下[9]

(8)

2.2 AKPSO模型

根据文献[10]，PSO算法中粒子的速度、位置、个体最优位置、全局最优位置共同组合构成的状态是一个Markov状态，即：下一时刻的状态空间仅仅与前一时刻的状态空间有关，且状态空间为可列集，粒子不同时刻的状态序列构成Markov链。考虑最小化优化问题，则重新列写PSO算法方程为

(9)

其中

(10)

(11)

其中,Φk,k-1为系统状态转移矩阵，且

Φk,k-1=

将式(9)的前两式改造如下

(12)

令Zk=[zpk;zvk]，则系统观测方程为

(13)

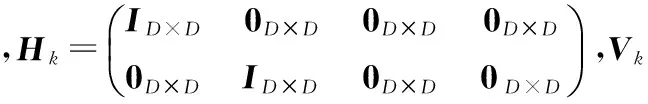
对式(11)和式(13)采用指数加权的自适应衰减记忆Kalman滤波，其滤波方程如下:

一步预测均方误差阵为

(14)

滤波增益为

(15)

状态一步预测值为

(16)

状态估计值为

(17)

估计均方误差为

(18)

预测均方误差为

=eα·Pk+1,k.

(19)

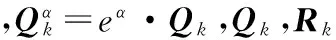
通过公式(20)变换得到粒子的新位置

(20)

AKPSO算法框架图如图1所示。

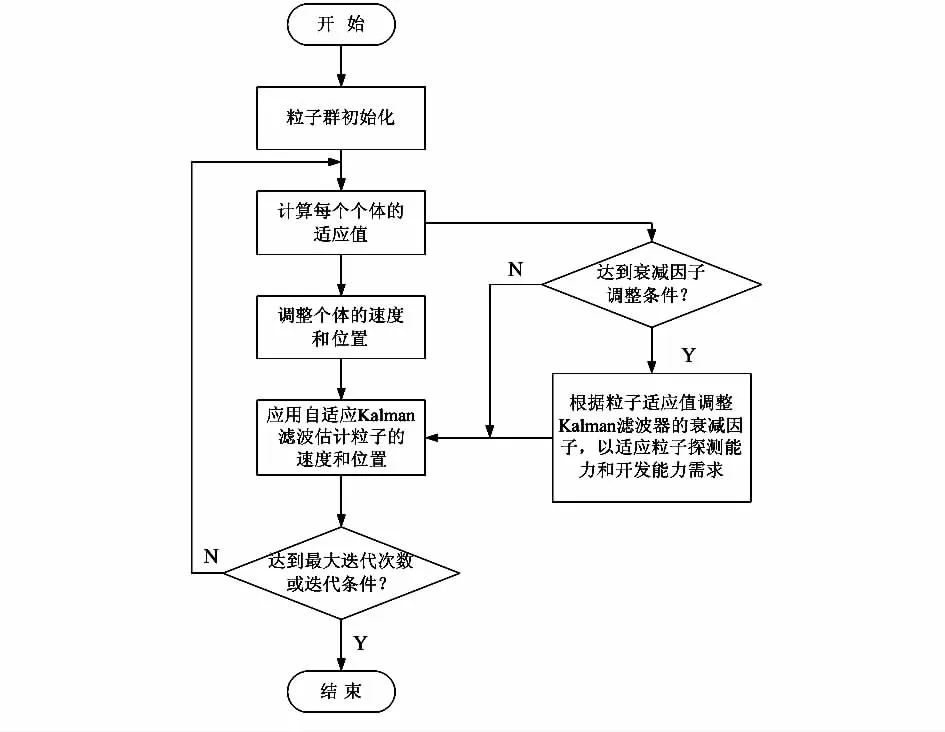
图1 AKPSO算法框架图

3 基于AKPSO算法的加速度计标定

3.1 参数设置

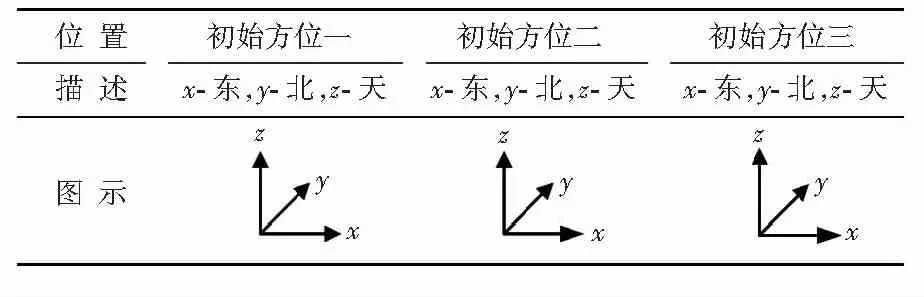
加速度计待标定参数有12个，要完全激励出所有参数需要在至少12个不相关的位置进行观测，根据目标函数的形式可知，进行位置观测数越多，标定精度越高，为了提高参数标定精度，本文在仿真中取24个位置进行观测，三种基本初始方位放置如表1所示，在每一基本初始方位下，又变换8种方位。第一种初始方位y轴指北，以45°间隔绕y轴转动，变换8个方位；第二种初始方位x轴指北，以45°间隔绕x轴转动，变换8个方位；第三种初始方位z轴指北，以45°间隔绕z轴转动，变换8个方位，共计24个位置。

表1 位置观测的三种初始方位

Tab 1 Three initial positions of observation

为了验证AKPSO算法在加速度计标定中的应用性能，仿真中将AKPSO算法与KPSO，PSO算法进行对比仿真。具体参数设置为：粒子种群规模N=500，粒子维数D=12，加速因子c1=c2=2，迭代步数500步，PSO算法惯性权重w=0.728 9，系统自适应Kalman滤波的状态初值为0，初始估计均方差P0=εdiag(w,w,w,w)，ε调整常数，w是粒子位置边界条件组成的行向量；系统过程噪声方差阵初值Q0=εdiag(w,w,w,w)；观测噪声方差阵初值为R0=εdiag(w,w)。

3.2 标定结果与分析

在仿真过程中，为了避免四舍五入造成的算法性能无法区分，标定结果多取了一位，标定仿真结果如表2和图2所示。

图2 加速度计标定适应度函数曲线

结合图2和表2的加速度计标定结果可以得出：在加速度计标定优化中，AKPSO算法在收敛速度、收敛精度方面都要优于PSO,KPSO算法，有效地提高了加速度计的标定精度。

表2 加速度计的标定结果

4 结 论

本文从工程实际需要的角度出发，提出了AKPSO算法，并将其成功应用于加速度计快速标定。该算法利用粒子群状态空间Markov链模型，建立了粒子群系统状态方程和观测方程；采用指数加权的自适应衰减记忆Kalman滤波来对粒子的位置进行估计。加速度计标定仿真结果表明:AKPSO算法在收敛速度、收敛精度方面都要优于PSO,KPSO算法，有效地提高了加速度计的标定精度。

[1] Lötters J C,Schipper J,Veltink P H,et al.Procedure for in-usecalibration of triaxial accelerometers in medical applications[J].Sensors and Actuators A:Physical,1998,61(1):221-228.

[2] Skog I,H Ndel P.Calibration of a MEMS inertial measurement unit[C]∥XVII IMEKO World Congress,2006.

[3] Fong W,Ong S,Nee A.Methods for in-field user calibration of an inertial measurement unit without external equipment[J].Mea-surement Science and Technology,2008,19(8)：085202-085213.

[4] Syed Z,Aggarwal P,Goodall C,et al.A new multi-position calibration method for MEMS inertial navigation systems[J].Mea-surement Science and Technology,2007,18(7):1897-1907.

[5] Kennedy J,Eberhart R C.Particle swarm optimization[C]∥Proceedings of IEEE International Conference on Neural Networks,Piscataway,New Jersey,1995:1942-1948.

[6] Monson C K,Seppi K D.The Kalman swarm:A new approach to particle motion in swarm optimization[C]∥Proceedings of the Genetic and Evolutionary Computation Conference,Springer,2004:140-150.

[7] Suresh Chandra Satapathy,Suresh Chittineni,Mohan S Krishna,et al.Kalman particle swarm optimized polynomials for data cla-ssification[J].Applied Mathematical Modeling,2012,36(1):115-126.

[8] 张红良.陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D].长沙：国防科学技术大学,2010.

[9] 潘 峰,周 倩,李位星,等.标准粒子群优化算法的马尔科夫链分析[J].自动化学报,2013,39(4):381-389.

[10] 廖振兴,钟伟民,钱 锋.基于高斯白噪声扰动变异的粒子群优化算法[J].华东理工大学学报：自然科学版,2008，34(6):859-863.

Rapid calibration method for accelerometerbased on AKPSO algorithm*

DAI Shao-wu1, WANG Ke-hong1, QIAN Jian-xue2

(1.Department of Control Engineering,Naval Aeronautical and Astronautical University,Yantai 264001,China； 2.92349 Unit of PLA,Zibo 255178,China)

Aiming at premature and trapped in a local optimum which appeared in calibration optimization of accelerometer based on particle swarm optimization(PSO)algorithm and insufficience which existed in design and application process of Kalman PSO(KPSO)algorithm,an improved PSO algorithm based on adaptive Kalman filtering(AKPSO)is proposed and it is applied successfully to fast calibration of accelerometer.Using particle swarm state space Markov chain model,state equation and observation equation of particle swarm system are established;exponentially weighted adaptive attenuation memory Kalman filtering is used to estimate position of particle.Simulation result of accelerometer calibration shows that the proposed algorithm is better than PSO and KPSO algorithm in both convergence speed and convergence precision,and it can effectively improve calibration precision of accelerometer.

calibration of accelerometer; adaptive Kalman PSO(AKPSO); Markov chain model

2014—07—03

中国博士后科学基金资助项目(2013M532173)； 航空科学基金资助项目(20135184007)

10.13873/J.1000—9787(2015)02—0069—04

U 666.1; TP 18

A

1000—9787(2015)02—0069—04

戴邵武(1966-)，男，湖南邵阳人，博士，教授，研究方向为惯性导航、组合导航、人工智能。