改进型最小二乘法的RBS时间同步算法

RBS Time Synchronization Algorithm using Improved Least Square Method

闫安斌1,2　刘文怡1,2　石永亮1,2　关咏梅3

(中北大学电子测试技术国家重点试验室1， 山西 太原　030051；

仪器科学与动态测试教育部重点试验室2，山西 太原　030051；北京宇航系统工程研究所3,北京 100076)

改进型最小二乘法的RBS时间同步算法

RBS Time Synchronization Algorithm using Improved Least Square Method

闫安斌1,2刘文怡1,2石永亮1,2关咏梅3

(中北大学电子测试技术国家重点试验室1， 山西 太原030051；

仪器科学与动态测试教育部重点试验室2，山西 太原030051；北京宇航系统工程研究所3,北京 100076)

摘要：传统最小二乘法对奇异点比较敏感。当样本中存在奇异点时，不能客观反映数据的真实分布情况；而传统最小一乘法计算量太大，不能实时处理数据。针对经典RBS算法在确定节点本地时钟之间的相对时钟漂移率和偏移值时，采用传统最小二乘法会导致时钟同步收敛速度太慢的问题，提出了一种改进型的最小二乘法。该算法能够有效地识别和剔除样本容量中的奇异点。经试验证明，该方法能够改进节点之间的时钟同步效果和收敛速度。

关键词：最小二乘法最小一乘法RBS时间同步算法时钟漂移时钟偏移

Abstract：The traditional least square method is comparatively sensitive to singular points, when singular point exists in sample, real actual distribution of the data cannot be reflected; while the traditional least one multiplication method is too computationally intensive, data cannot be processed in real time. Aiming at classical reference-broadcast synchronization (RBS) algorithm, due todetermine the relative clock drift rate and offset value between local clock of the nodes by adopting traditional least square method may lead to the convergence speed is too slow, thus the improved least square method is proposed. With this method, the singular points in sample size can be effectively recognized and excluded. The tests prove that by using this method, clock synchronous effect and convergence speed between nodes can be greatly improved.

Keywords：Least square methodLeast one multiplication methodRBS time synchronization algorithmClock driftClock offset

0引言

分布式无线传感网络(wireless senor network,WSN)机制中，各节点之间本地时间的同步是网络进行目标定位、跟踪的首要条件，很多建立在这些分布式网络之上的系统，都要求网络中的节点之间能有一个统一的、准确的时钟，保证正常的协调工作和运行。目前国内外已经出现了较多WSN时间同步算法，(reference broadcast synchronization，RBS)是较为典型且使用较为普遍的一种。本文结合设计节点的实际使用环境和节点使用时对时间同步精度的要求，综合考虑各种因素，采用RBS时间同步算法作为节点时间同步的基本算法。

1RBS时间同步算法简介

参考广播同步算法RBS适用于分布式节点之间的时间同步，是目前分布式节点时间同步算法中使用最为普遍的一种。使用者往往根据自己所设计的节点及节点使用环境的不同，基于RBS算法融入不同的数学思想，衍生出了许多不同的算法。相比较而言，该算法较LTS、TPSN等算法协议，同步精度更高。

RBS算法利用了无线信号在链路层传输的广播信道特性[4]，将分布式无线节点分为发送节点和接收节点两种。发送节点发送一组广播消息，周围的接收节点监测发送节点发出的广播信号，当接收节点检测到广播信号之后，将接收时刻的时间戳存储起来，各接收节点之间相互交换各自接收到的广播消息的时间戳。各节点根据接收到的其他节点的一组时间戳信息，结合自身对应的一组时间戳信息，利用线性回归法计算两节点时钟的相对时间漂移。通过计算，采用对时钟晶振进行补偿的方法，减小两节点之间的时钟漂移，多次修正使节点间的时钟漂移值趋近于0。再利用两节点相对应的两组本地时间戳信息，计算两节点每次同步之后的时间相对偏移，并求取这些数据的平均值。该平均值即作为两节点之间的本地时间的时钟偏移量，从而对其中一个节点的本地时间进行修正，以使两节点的本地时间偏移量趋近于0。

经过多次交换时间戳信息，可以得到多组相应的数据。利用上述计算方法对节点时间进行多次修正，最终实现接收节点之间的时间同步。同步示意图如图1所示。

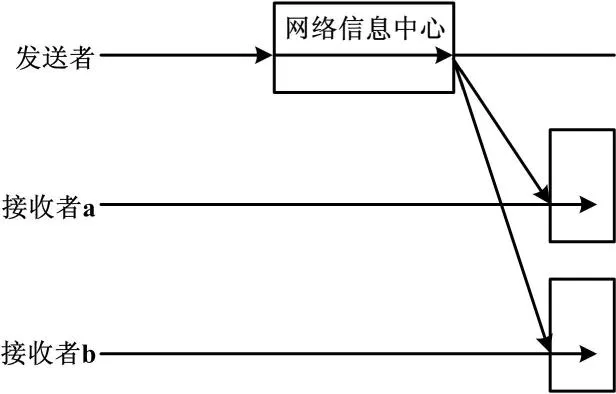
图1　RBS同步机制基本原理

RBS算法中，发送节点广播一个信标分组，广播域中的一组(此处示意为两个)接收节点都能接收到这个分组，并记下信标到达时间戳。接收节点间相互交换接收时间，两个接收时间的差值相当于两个接收节点间的时间差值，其中一个节点可以根据这个时间差值更改它的本地时间，从而实现两个节点的时间同步。区域中其他节点的同步与此类似。

2改进型最小二乘法

RBS时间同步算法要求能够准确快速地利用采集得到的时间戳信息，拟合出关于时间的一次函数。根据得到的各节点的时间函数，确定节点间的时钟漂移率和偏移值，从而实现时间同步。较常使用的线性拟合方法有最小一乘法和最小二乘法两种。

2.1　传统最小一乘法与最小二乘法

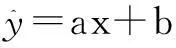
(1)

(2)

求解该函数中a与b的值，只需对式(2)中的a与b分别求偏导并令其为零，即令：

(3)

若其系数行列式不为零，则可求得唯一的a、b的值。该值即为所求的线性回归的回归系数[5]。

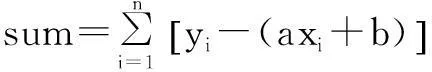
2.2　改进型最小二乘法

RBS同步算法中提出了对待同步节点的本地时钟，进行时钟漂移和时钟偏移补偿的要求。这就需要采用线性拟合的运算方法对采样得到的时间点集合进行拟合运算，从而得到节点本地时钟相对于参照节点的时钟漂移率和时钟偏移值。近年来，围绕线性拟合运算不断有新的研究成果，其中较为典型的有最小一乘法和最小二乘法[1-2]。这两种拟合运算对线性的拟合各有优劣。最小一乘法数据运算量太大，对数据不能够实时处理，导致耗能多，与节点的节能设计思想相背离；最小二乘法数据运算量虽小，但个别奇异点对其计算结果的影响比较大[3]，而节点数据传输中难免出现奇异点，故本文采用改进型的最小二乘法计算节点的时钟斜率和时钟偏移量，提高节点时钟同步的收敛速度。

选手参赛类节目或活动中，在最终评委打分的环节，常常可以听到主持人讲：去掉一个最高分，去掉一个最低分。为什么需要去掉最高分和最低分，就是为了减小最高分和最低分对选手成绩的影响。在这不妨认为最高分和最低分就是样本容量中的奇异点。参照这种思路，在使用RBS同步算法进行节点同步时，样本容量中难免会有奇异点的存在。

鉴于最小一乘法计算量太大，对数据不能实时处理，节点耗能也不满足节能的设计思想；最小二乘法对奇异点敏感度太高，当有奇异点存在时，不能客观反映真实情况。综合考虑，提出了一种改进型的最小二乘法。本次改进型最小二乘法的算法示意图如图2所示。

图2　改进型最小二乘法算法流程图

图2中，判断采集样本中的采样点是否为奇异点，是通过计算该点与其相邻的下一个采样点的差值，并判断这个差值是否为负数。若为负数，则认为该点为奇异点；否则，将不是奇异点。

由于本次最小二乘线性拟合的使用环境为RBS算法的时间同步，时间是不可逆的，故在本次算法改进中只需判断下一个节点的数据是否大于上一个节点的数据即可。经大量试验证明，上述判断准则对该算法中的奇异点的去除效果很明显，且误判率很低。该改进型最小二乘算法对含有奇异点的样本容量的直线拟合效果很好，能够真实地反映这些数据样本的真实情况。

3RBS误差分析

全面而准确地分析传感节点之间时间同步误差产生因素，是正确使用RBS[7]同步算法的前提。根据RBS同步示意图，结合其他同步协议，不难看出利用RBS同步，接收节点不需要与发送节点同步，其忽略了发送节点发送数据产生的发送延时误差和发送报文形成的延时误差。下面是引起RBS同步误差的主要因素。

① 晶振频率引起的误差：晶振的振荡频率与其形状、材料、切割方向等密切相关，虽然根据目前的技术，晶振的几何尺寸可以做到很精密，但晶振的振荡频率尚不能实现完全相等，仍存在一定的频率偏差。

② 信标分组在介质中传播产生时间误差：信标分组为无线电磁波信号，该信号在空气中传播极易受外界的影响，传播过程中所用的传播时间不确定；其次，该无线传感器网络节点是随机地使用播撒方式散布在监测区域中，所以每个接收节点距离发送节点的距离为不确定的值，这两者使得信标分组在介质中传播时间的不确定性增大，直接影响节点时间同步的精度。

③ 接收节点数据处理延时误差：由于节点要求体积尽量小，其自身携带的能量有限，所以节点的数据处理能力有限，在接收到信息的时候，难免会由于各种因素导致节点的反应时间不同而产生误差。

4试验仿真

采用OMNET++模拟无线传感网络节点之间的时间同步，同步方式采用RBS方式，模拟节点之间每间隔5 ms同步一次，并在此次同步中强加一次同步错误，生成一个奇异点。本次模拟同步10次，相关数据如表1所示。

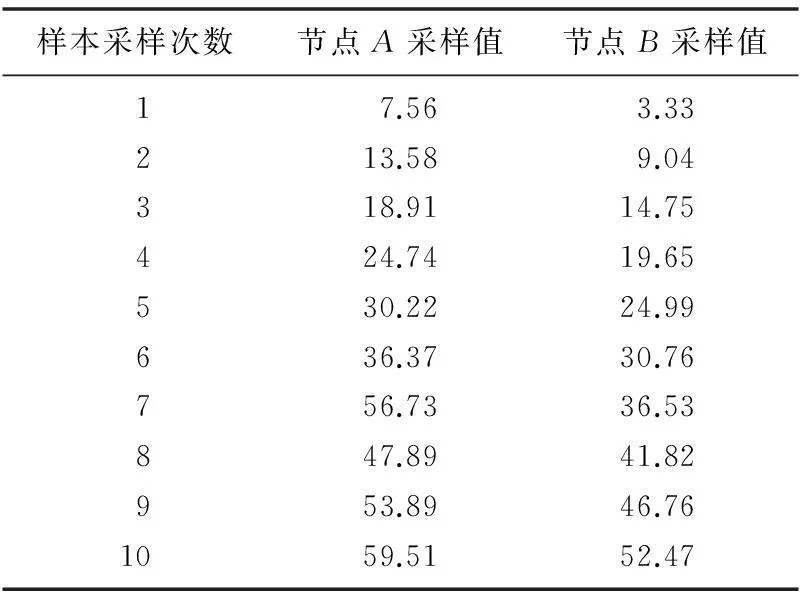
表1　时间采样数据容量

表1中,给定节点A和B各一个初始值，值的大小不定且不等，利用Matlab,对上述数据分别使用最小一乘法、最小二乘法和本文中提出的改进型最小二乘法进行线性拟合，拟合后的结果如图3所示。

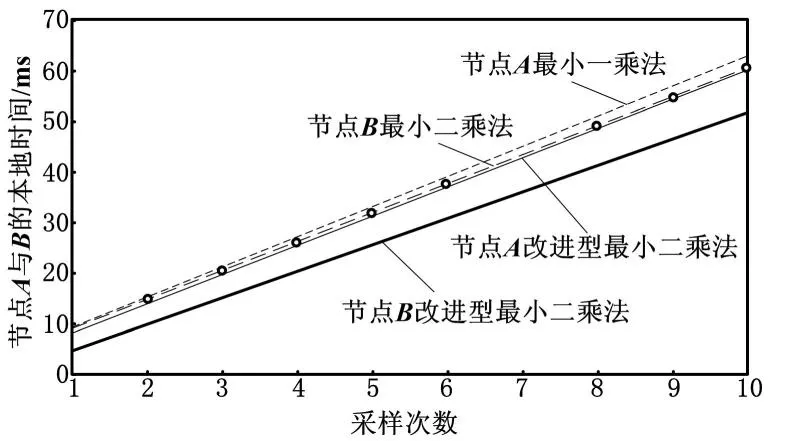
图3　Matlab仿真RBS同步示意图

从图3可以看出，利用最小一乘法和改进型最小二乘法拟合出的直线相接近，能够比较真实地反映出样本点分布的真实情况。而最小二乘法因为奇异点的存在，拟合出的直线与最小一乘法和改进型最小二乘法拟合出的直线相偏离，不能客观地反映出样本点分布的真实情况。图4是节点A与B分别根据最小二乘法和改进型最小二乘法拟合出的直线，经一次同步后的两节点本地时钟模型示意图。

图4　一次同步后的节点之间的本地时钟模型

从图4可以很直观地看出，当有奇异点存在时，采用最小二乘法拟合出的直线，对时钟进行漂移和偏移补偿的效果很不明显，甚至使得补偿出现偏差；采用改进型的最小二乘法，补偿后的效果较为明显，节点之间的时间同步有很大的改观。

5结束语

节点时间同步是无线传感网络的一项重要的支撑技术，不同的使用环境，需要选用不同的同步算法。根据本次设计的无线传感网络的使用环境，综合考虑后，选择使用RBS时间同步算法，但由于经典RBS算法中对节点本地时间的线性拟合，采用传统最小二乘法，而传统最小二乘法对奇异点太敏感，使得同步效果不太明显，故本文提出了一种改进型的最小二乘法。该方法能有效地判定并去除奇异点，对时钟同步的收敛速度有了很明显的改观。

参考文献

[1] 李雄军.几种线性回归方法的比较[J].计量技术，2005(8)：52-54.

[2] 李仲来.最小一乘法介绍[J].数学通报，1992(2)：42-45.

[3] 王文平.从算术平均数谈最小一乘法与最小二乘法的区别[J].武汉船舶职业技术学院学报，2009(6)：40-41.

[4] 王汝传，孙力娟.无线传感器网络技术及其应用[M]．北京：人民邮电出版社，2011:168-169.

[5] 张旭峰，王志斌，王秉仁.大学物理试验[M].北京：机械工业出版社，2010.

[6] 王文峰.基于LINGO的最小一乘线性回归的参数估计[J].贵州财经学院学报，2006(6):106-108.

[7] Zhen Chengfang,Liu Wenyi,Hou Yulong.An accurate on-demand reference broadcast synchronization protocol for wireless sensor network[J].Sensor & Transducers,2013,154(7):42-50.

中图分类号：TN92;TH89

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201507003

修改稿收到日期：2014-08-27。

第一作者闫安斌(1989-)，男，现为中北大学电子与通信工程专业在读硕士研究生；主要从事声定位无线传感网络的研究。