一种离散模糊滑模边界层自适应的消抖方法

Method of Eliminating Chattering Based on Boundary Layer Adaption for Discrete Sliding Mode Control

张晓宇　陈文卓　申　斌

(华北科技学院电信学院，河北 三河　065201)

一种离散模糊滑模边界层自适应的消抖方法

Method of Eliminating Chattering Based on Boundary Layer Adaption for Discrete Sliding Mode Control

张晓宇陈文卓申斌

(华北科技学院电信学院，河北 三河065201)

摘要：在离散滑模控制中抖振非常常见。针对一类离散非线性系统的滑模控制抖振问题，在连续系统边界层自适应方法的基础上，提出一种带边界层自适应的近似滑模模糊逻辑控制方法。首先通过一定的自适应律对滑模边界层参数进行在线调整，然后将边界层自适应的SMC应用到模糊逻辑控制逼近实现中，使抖振得以削弱，且系统非线性动态不需要已知其上边界，使得整个闭环系统具有较强的鲁棒性、稳定性和自适应性等优点。仿真验证了该方法的正确性和优越性。

关键词：离散非线性系统滑模控制模糊自适应边界层 是论文的检索标志，是表达文献主题概念的自然语言词汇，一般是词和词组。

Abstract：In discrete sliding mode control, chattering phenomenon is very common. For solving chattering problem of sliding mode control for discrete nonlinear system, on the basis of boundary layer adaptive method of continuous systems, the sliding mode like fuzzy logic control method is proposed. Firstly, online adjustment of boundary layer parameters is conducted through certain adaptive laws; then the SMC with boundary layer adaptation is applied in fuzzy logic control approximation implementation. Thus the chattering can be weakened, while, the entire closed loop system offers stronger robust stability and adaptation. The correctness and superiority of this method are verified by simulation.

Keywords：DiscreteNonlinear systemSliding mode control (SMC)FuzzyAdaptiveBoundary layer

0引言

滑模控制(sliding mode control,SMC)有抖振的缺点[1-2]，但模糊逻辑系统的应用可改进其性能。关于模糊滑模控制(fuzzy sliding mode control,FSMC)[3-14]和滑模模糊逻辑控制(sliding mode fuzzy control,SMFC)[10,15-20]已有大量研究。

Lee C G和Park J S等人提出近似滑模模糊逻辑控制(sliding mode-like fuzzy control,SMLFC)[20]，方法是将模糊控制器等价于滑模控制器设计且边界层厚度可在线自调整，通过引入适当的自适应律来消除抖振。该方法只适用于二阶系统，如果死区参数不收敛到零，仍会有微弱抖振。对于高阶动态非线性系统，控制器的设计应采用不同的方式，其中对高阶动态非线性系统的SMLFC已被提出[21]，但其仅适用于连续系统。

针对离散非线性系统，提出与上述类似的方法，同样运用在线自适应调节饱和函数和SMC死区参数的思想，推出近似滑模模糊控制设计[20]。应用动态模糊逻辑系统(dynamic fuzzy logic system,DFLS)获得平滑的控制性能，再通过DFLS形成近似滑模模糊控制(sliding mode-like fwey logic control,SMLFC)系统，彻底消除抖振。

1离散滑模控制及存在问题

滑模控制在有限时间内将系统从初始状态驱动到切换函数所决定的一个超平面上并维持。系统状态到达超平面的过程称为到达过程；系统状态在滑模面上的运动称为滑模运动；超平面称为滑模面。在离散时间情况下，描述滑动模态的性质、存在及到达条件都会改变。随着计算机技术的高速发展和工业自动化等领域的实际需要，控制算法的实现经常需要采用数字计算机。因此，研究离散时间系统的滑模变结构控制方法具有很好的理论价值和实际意义。

滑模变结构控制包含三个基本问题：滑动模态的存在性、可达性及稳定性。这也是离散时间系统滑模变结构控制的基本问题，但离散时间系统自身的固有特点使得其与连续时间系统有所不同[2]。

离散时间滑模控制的不变性对于参数摄动和外部干扰，都可以通过控制律u(k)的适当设计来进行补偿或抵消。因此，离散时间系统和连续时间系统一样，对系统的参数摄动及外干扰是不变的，只要其充分必要条件能得到满足，即摄动与干扰的条件匹配。

然而，当采用数字计算机实现滑模变结构控制算法时，由于采样过程的限制，理想的滑动模态是不存在的，状态运动轨迹只能以抖振形式在切换面的某一邻域内运动并渐近趋向原点或原点的一个邻域。 所以，对于离散时间系统，滑模变结构控制不能产生理想的滑动模态控制，只能产生准滑动模态(quasi-slidingmode,QSM)控制。尤其在系统不确定性、外扰严重的情况下，为了依然满足不变性，滑模控制抖振更严重。

2离散非线性系统及边界层算法

考虑如下一类非线性系统。

(1)

(2)

(3)

(4)

式中：向量c可以构成一个Hurwitz 多项式。

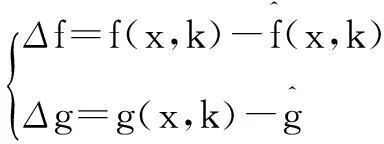
(5)

(6)

根据基本滑模控制理论[2]，如果滑模控制输入u可以构造为：

(7)

其中：

(8)

φ=δ+η+ε

(9)

式中：φ为边界层的厚度；参数η>0和ε>0为正标量，可以选很小；k1按下式给出。

(10)

因此到达条件：

(11)

若式(11)可以满足，则系统追踪误差向量e是有界的。

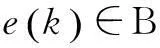
证明：

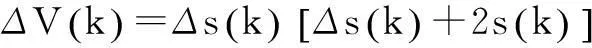
那么式(11)成立等价于：

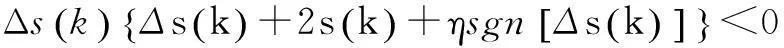
(12)

根据式(1)~式(6)，有：

(13)

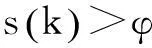
这意味着不等式(12)是可以满足的。

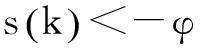
这意味着不等式(12)也是可满足的，则式(11)是成立的。根据Lyapunov理论,切换带B是可达并稳定的。

若Δf=Δg=0，由式(13)有：

因此，参数γ和δ都是未知的，控制式(7)是不能实现的，因为k1和φ不能确定。而下面的内容可以说明边界层自适应问题是可以解决的。

3边界层自适应方法

(14)

证明：

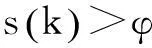
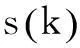
如果把到达条件(14)再稍作改进，变为：

(15)

这里λ1、λ2>1是任意可选的正标量参数。那么有以下定理。

证明：

(16)

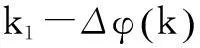
(17)

(18)

证明:

选择一个 Lyapunov函数:

(19)

然后得出Lyapunov函数V的导数随着时间k沿着闭环系统的轨迹,则:

那么式(15)成立等价于:

Δs(k){2Δs(k)+2s(k)+

[η-λ1Δφ(k)-λ2|s(k)|]sgn[Δs(k)]}+

(20)

根据式(13)，有:

(21)

根据式(18)，有:

(22)

根据式(16)，有：

(23)

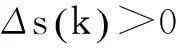
Δs(k){Δf+Δgueq-γk1+(γ-1)k1+

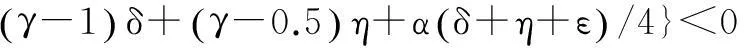
这意味着式(22)成立。

4基于边界层自适应SMC的模糊控制

上述边界层自适应方法已经证明滑模切换带可以保证到达。但是边界层自适应的方法本身由于存在饱和函数(符号函数)，抖振的本质仍然存在。为了进一步消抖，引入动态模糊逻辑系统方法[21]。

DFLS的表达式为:

(24)

推理规则是IF…THEN…语句。DFLS的模糊推理规则表如表1所示。

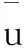
(25)

然后，φ可以由自适应律(18)在线调节，而自适应律(17)并没有使用。由于φ是DFLS前件划分参数,因此模糊逻辑系统的在线自调整得以实现。这样，将获得一个近似滑模模糊控制(SMLFC)系统。

表1　DFLS的模糊推理规则表

5仿真实例

考虑一阶倒立摆系统离散模型，如下所示：

图1　倒立摆的摆角位移曲线图

图2　控制电压曲线图

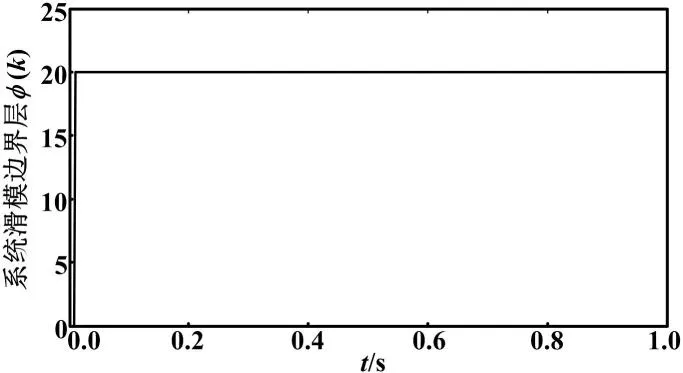
图3　边界层参数曲线图

与文献[10]一样，设跟踪信号为yd=0.1sinπt，采样时间Ts=0.01 s(文献[10]为连续控制)，其他参数如前，得到的摆角位移曲线结果如图4所示，控制电压的曲线对比图如图5所示。

图4　倒立摆的摆角位移曲线对比图

图5　倒立摆的控制电压曲线对比图

从图4和图5中不难明显对比得出，本文控制效果更佳，响应更快，过渡过程更小。尤其是本文的控制方法在稳态时没有抖振，说明本文提出的SMLFC方法优于文献[10]的模糊自适应控制效果。

从倒立摆的应用仿真可以看出，控制效果完全达到了预期。边界层的引入使滑模到达准切换带有了保障，而且DFLS的引入使控制信号有了滤波功能，高频抖振被滤除。在文献[20]中φ也是趋于常数，研究如何保证在滑模到达的前提下趋于零，这样消抖效果会更好。这有待于进一步研究。

6结束语

首先设计了适合的自适应律，以在线调整边界层，削弱抖振，然后通过引入一个动态模糊逻辑系统逼近SMC控制律，使控制信号具有滤波功能，滤除高频抖振。系统的切换带能保证到达条件得到满足。倒立摆应用仿真证明了所提出方法的正确性和有效性。

参考文献

[1] Utkin V I.Variable structure systems with sliding modes[J].IEEE Transactions on Automatic Control,1977,22(2):212-222.

[2] Edwards C,Spurgeon S K.Sliding mode control:theory and applications[M].London(UK):Taylor & Francis,1998.

[3] 李继超,管萍,刘小河.间接自适应模糊滑模控制在电弧炉中的应用[J].系统仿真学报,2009,21(2):542-546.

[4] 席雷平,何辉,董海瑞.机械臂轨迹跟踪滑模控制中的抖振抑制法研究[J].计算机仿真,2012,29(5):188-191.

[5] 董小闵,余淼,廖昌荣,等.具有非线性时滞的汽车磁流变悬架系统自适应模糊滑模控制[J].振动与冲击,2009,28(11):55-60，203.

[6] 张金萍,刘阔,林剑峰,等.挖掘机的4自由度自适应模糊滑模控制[J].机械工程学报,2010,46(21):87-92.

[7] 赵红超,徐君明,王东.变质心弹头的自适应模糊滑模控制[J].清华大学学报：自然科学版,2008(S2):1733-1736.

[8] 彭亚为,陈娟,刘占富,等.自适应模糊滑模控制在化工过程中的应用[J].化工学报,2012,63(9):2843-2850.

[9] Hwang Chih-Lyang,Wu Hsiu-Ming,Shih Ching-Long，et al.Fuzzy sliding-mode under actuated control for autonomous dynamic balance of an electrical bicycle[J].IEEE Transactions on Control Systems Technology,2009,17(3):658-670.

[10]刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社,2005.

[11]Ho T H,Ahn K.Speed control of a hydraulic pressure coupling drive using an adaptive fuzzy sliding-mode control[J].IEEE/ASME Transactions on Mechatronics,2012,17(5):976-986.

[12]Zhu M C,Li Y C.Decentralized adaptive fuzzy sliding,mode control for reconfigurable modular manipulators[J].International Journal of Robust and Nonlinear Control,2010,20(4):472-488.

[13]Shahraz A,Bozorgmehry B R.A fuzzy sliding mode control approach for nonlinear chemical processes[J].Control Engineering Practice,2009,17(5):541-550.

[14]Ho H F,Wong Y K,Rad A B,et al.Adaptive fuzzy sliding mode control with chattering elimination for nonlinear SISO systems[J].Simulation Modelling Practice and Theory,2009,17(7):1199-1210.

[15]Guo Liping,Hung J Y,Nelms R M,et al.Comparative evaluation of sliding mode fuzzy controller and PID controller for a boost converter[J].Electric Power Systems Research,2011,81(1):99- 106.

[16]Poursamad A,Davaie-Markazi A H.Robust adaptive fuzzy control of unknown chaotic systems[J].Applied Soft Computing,2009,9(3):970-976.

[17]Hsu C F,Chung I F,Lin C M,et al.Self-regulating fuzzy control for forward DC-DC converters using an 8-bit microcontroller[J].IET Power Electonics,2009,2(1):1-13.

[18]Lin W S,Chen C S.Sliding-mode-based direct adaptive fuzzy controller design for a class of uncertain multivariable nonlinear systems[C]//Proceedings of the American Control Conference,2002:2955-2960.

[19]Wai R J,Lin C M,Hsu C F.Self-organizing fuzzy control for motor-toggle servomechanism via sliding mode technique[J].Fuzzy Sets and Systems,2002,131:235-249.

[20]Lhee C G,Park J S,Ahn H S,et al.Sliding mode-like fuzzy logic control with self-tuning the dead zone parameters[J].IEEE Transactions on Fuzzy Systems,2001,9(2):343-348.

[21]Zhang X Y,Su H Y,Chu J.Adaptive sliding mode-like fuzzy logic control for high-order nonlinear systems[C] //Proceedings of the 2003 IEEE International Symposium on Intelligent Control,2003:788-792.

科技期刊关键词和引言的撰写

科技论文的关键词是从其题名、摘要和正文中选出来的。关键词包括3部分：1)叙词(正式主题词)，经过规范化的并收入主题词表中的词或词组；2)非正式主题词(词表中的上位词+下位词+替代词)；3)自由词(标引需要但主题词表中找不到的词)。

每篇论文中应专门列出3~8个关键词，其中叙词应尽可能多一些。关键词作为论文的组成部分，置于摘要段之后。

引言又称前言或绪论，是论文整体的有机组成部分。引言写在正文之前，属于整篇论文的引论部分。它的作用是向读者初步介绍文章内容。

引言要写得自然、概括、简洁、确切。引言中要写的内容大致有如下几项：1)研究的理由、目的和背景 ；2)理论依据、实验基础和研究方法；3)预期的成果及其作用和意义。

引言的写作要求是：1)开门见山，不绕圈子。注意一起笔就切题，不能铺垫太远；2)言简意赅，突出重点；3)尊重科学，不落俗套。

引言中要求写的内容较多，而篇幅有限，这就需要根据研究课题的具体情况确定阐述重点。共知的、前人文献中已有的不必细写，主要写好研究的理由和目的，使读者对论文有一个总体的了解。

中图分类号：TH71;TP273+.2

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201508001

国家自然科学基金青年科学基金资助项目(编号：61304024)；

河北省自然科学基金青年科学基金资助项目(编号：F2013508110)；

中央高校基本科研业务费资助项目(编号：3142013055)；

河北省教育厅科技计划基金资助项目(编号：Z2012089)。

修改稿收到日期：2014-12-26。

第一作者张晓宇(1978-)，男，2006年毕业于浙江大学控制科学与工程专业，获博士学位，副教授；主要从事非线性控制、智能控制、复杂系统控制与应用的研究。