基于目标拓扑参照图的雷达航迹抗差关联方法

李 明

(武汉市江夏区藏龙北路1号 武汉 430205)



基于目标拓扑参照图的雷达航迹抗差关联方法

李 明

(武汉市江夏区藏龙北路1号 武汉 430205)

针对雷达系统偏差影响下数据关联容易错误的问题,提出一种基于目标拓扑参照图的数据抗差关联新方法,该方法首先将目标进行聚类减少关联复杂度,再对聚类目标拓扑参照图经过平移、旋转和尺度等变换进行关联匹配,达到目标关联一致性的目的。仿真结果表明了该方法具有较高的关联精度和鲁棒性。

数据相关; 系统偏差; 聚类; 匹配

Class Number TN957; TP274

1 引言

在雷达系统偏差影响下实现多目标航迹相关是目前的重点、难点问题,传统的关联方法主要考虑航迹偏差在零均值条件下目标关联,难以满足实际应用的需求;而在工程应用中,雷达航迹往往或多或少的存在一定的航迹偏差、定姿定位等误差因素,所以,研究雷达具有系统偏差条件下的多目标航迹抗差关联方法是非常必要的。文献[1]最早开始航迹相关技术的研究,通过将在统计意义上与被跟踪目标预测位置最近的量测作为与目标关联的候选对象完成不同航迹之间的关联,但该方法仅适用于信噪比高、系统偏差较小以及目标密度小的条件。文献[2]提出利用不同航迹间关联的各种可能的情况,构造面向量测的关联假设树,借以实现多目标航迹的关联。它避免了NN方法“唯一性”可能造成的关联错误,能够较好地适应目标密环境下,系统存在一定的系统偏差,或交叉、分岔以及机动航迹较多的场合。但随着目标数的增加,可能出现使计算机的运算次数发生“组合爆炸”的现象,或者由于大量的“迭代”过程浪费许多时间。文献[3]提出利用模糊数学的隶属度概念描述航迹间的相似程度实现多目标航迹关联。通过一定的数据训练,该方法可以适应系统包含一定的导航、传感器校准以及转换或延迟误差等复杂情况下的目标相关;但是,当系统偏差较大时,该方法关联性能急剧下降。

本文提出一种对雷达系统偏差具有不敏性的关联方法[4～5],该方法运用“关联聚”思想将各雷达公共量测空间中较为密集的目标进行分类;再结合图论的方法,把聚类内的目标参照拓扑图经过平移、旋转和尺度等变换,实现图的关联匹配,以完成目标的关联。仿真实验证明,该算法可以有效地克服雷达系统偏差对航迹关联造成的影响。

2 关联聚类算法

关联聚类的目的主要是对目标空间进行区域划分,使得相关性较高的目标处于同一个区域内,降低目标关联的复杂性,同时也简化目标拓扑参照图的复杂度。对于关联聚类,我们采用K-均值聚类法[6～7],其基本思想是:该方法以K为参数,将n个待划分的对象分成K个类,以使类间具有较高的相似度,而类间的相似度较低。其相似度的计算根据一个类中对象的平均值进行,如图1所示。

图1 多雷达观测数据的聚类示意图

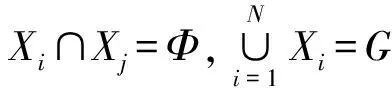
定义2(欧氏距离) 设任意对象xi,xj∈G,则对象xi,xj欧式距离为d(xi,xj)=|xi-xj|。

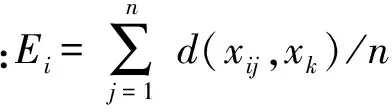
算法执行步骤:

Step1 从G中随机选择k个初始样本x1,x2,…,xk,分别作为聚类集合X1,X2,…,Xk的聚类中心,记作c1,c2,…,ck。同时迭代次数n=1。

Step2 对于∀xm∈G,但xm∉{c1,c2,…,ck},分别计算各聚类中心d(xm,ci),将xm归纳给欧氏距离最小的集合Xp,则Xp={xm,xp}。

Step3 重新计算聚类均值Ei和误差平方和Di。

Step4 迭代次数n++,直到Di不再发生变化,否则,返回Step2。

3 基于目标拓扑参照图匹配方法

目标关联的不确定性主要是由于雷达的系统偏差与随机误差的不确定性造成的。其中,随机误差可以通过滤波的方法进行消除,减弱其影响;但系统偏差是一种固有的、慢性的变化误差,目前消除的手段还不是很成熟。所以,雷达系统偏差是影响航迹关联的重要因素之一。通过分析发现,目标量测由于一定的系统偏差将导致运动轨迹与真实航迹发生严重偏离,但是单雷达空间目标拓扑参照关系并没有发生大的变化;此时,我们就会得到一个启示:对不同雷达公共量测空间目标分布关系形成一个拓扑参照图,再进行图与图之间的匹配关联;该方法能够很好的抵抗系统偏差对目标关联造成的影响,具有很高的关联精度。

基于目标拓扑参照图匹配[8～9]的基本思想是:将聚类内目标空间分布关系根据源不同形成多个拓扑参照图,以其中一个为参考图,依据假设的刚体变换模型,将输入图与参考图进行匹配关联,最后在匹配准则、关联检验等条件下实现多目标关联。

3.1 基于刚体变换模型的图匹配

配准的目的是消除两幅待配准图间的整体平移、旋转和尺度的差异,我们采用刚体变换模型[10],对聚类内两幅不同源探测的目标拓扑参照图进行配准,匹配公式如下:

(1)

其中,(x,y)和(x′,y′)分别为参考图与输入图对应图元的坐标,tx,ty表示x方向和y方向的位移,θ表示旋转角度,S表示尺度变化因子。在这种情况下,问题归结为一个四参数的最优化问题,如图2所示。

图2 雷达目标拓扑参照图

3.2 图匹配关联准则

根据定义5计算图2中两幅雷达观测目标图的重心,坐标分别为o(x,y),O(X,Y),设以雷达1观测目标的拓扑参照图为参考图,雷达2观测目标的拓扑参照图为输入图。任意选取两图中的顶点A与a,分别连接AO、ao,将顶点A平移到顶点a位置,得到tx,ty;以ao为轴旋转ABC,使得AO与ao重合,得到旋转角度θ;以ao为标准,对AO进行尺度变换,直到O与o重合,得到尺度因子S。再分别将得到的模型参数tx,ty,θ,S,代入B,C点,得到变换后的新的B,C点,如图3所示。

图3 雷达目标拓扑参照图匹配关联过程图

定义6(统计距离) 设两幅图中任意两顶点B、b,则两点统计距离为:d(B,b)=zTS-1z,其中z为滤波新息,S为新息协方差矩阵。

根据定义6,分别计算对应顶点的统计距离d(B,b)、d(C,c)。

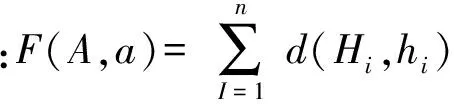
3.3 图匹配关联检验

定义8(关联检验) 设两幅图G1,G2关联成功的阈值为ξ,则满足Min(F)≤ξ。

依据3.2节的匹配关联准则,分别计算A与b、A与c、B与a、B与b、B与c、C与a、C与b、C与c各自的关联综合度F(gi,vj),根据定义7,选择最小的关联综合度进行判别。如果Min{F(gi,vj)}≤ξ,则代表对应顶点关联成功,否则,则关联失败。

ξ的取值,可根据自由度为M以及给定的落入概率P由χ2分布表中可以查到。

4 仿真实验

仿真实验在某多雷达融合系统仿真平台上完成,主要针对本文方法与文献[3]中方法进行了雷达航迹存在一定系统偏差情况下的仿真比较。设雷达1位于(10,10),雷达2位于(50,10),单位公里;两雷达误差分布服从N(±nσ,σ2),距离误差σd分别为300m、50m,方位误差σα分别为0.3°、0.1°;系统误差Δd、Δα为对应随机误差的n倍。模拟四批目标:目标1初始位置(40,20.8),目标2初始位置(40,20),目标3初始位置(30,40),目标4位置(20,20),单位公里;假设四批目标同时做匀速直线运动,运动方程为x=x0+6t,y=y0+8t,采样周期为2s,仿真测试200周期。

本文实验中雷达1的误差分布为N(nσ,σ2),雷达2的误差分布为N(-nσ,σ2),其中σ代表各自雷达的距离误差和方位误差,n=0.5,1.0,1.5,…,5.0,自由度为M=3以及给定的落入概率P=95%。则根据以上条件对四批目标的关联情况进行了10次仿真,如图4～图7所示。

图4 目标1关联正确率与系统偏差倍数关系图

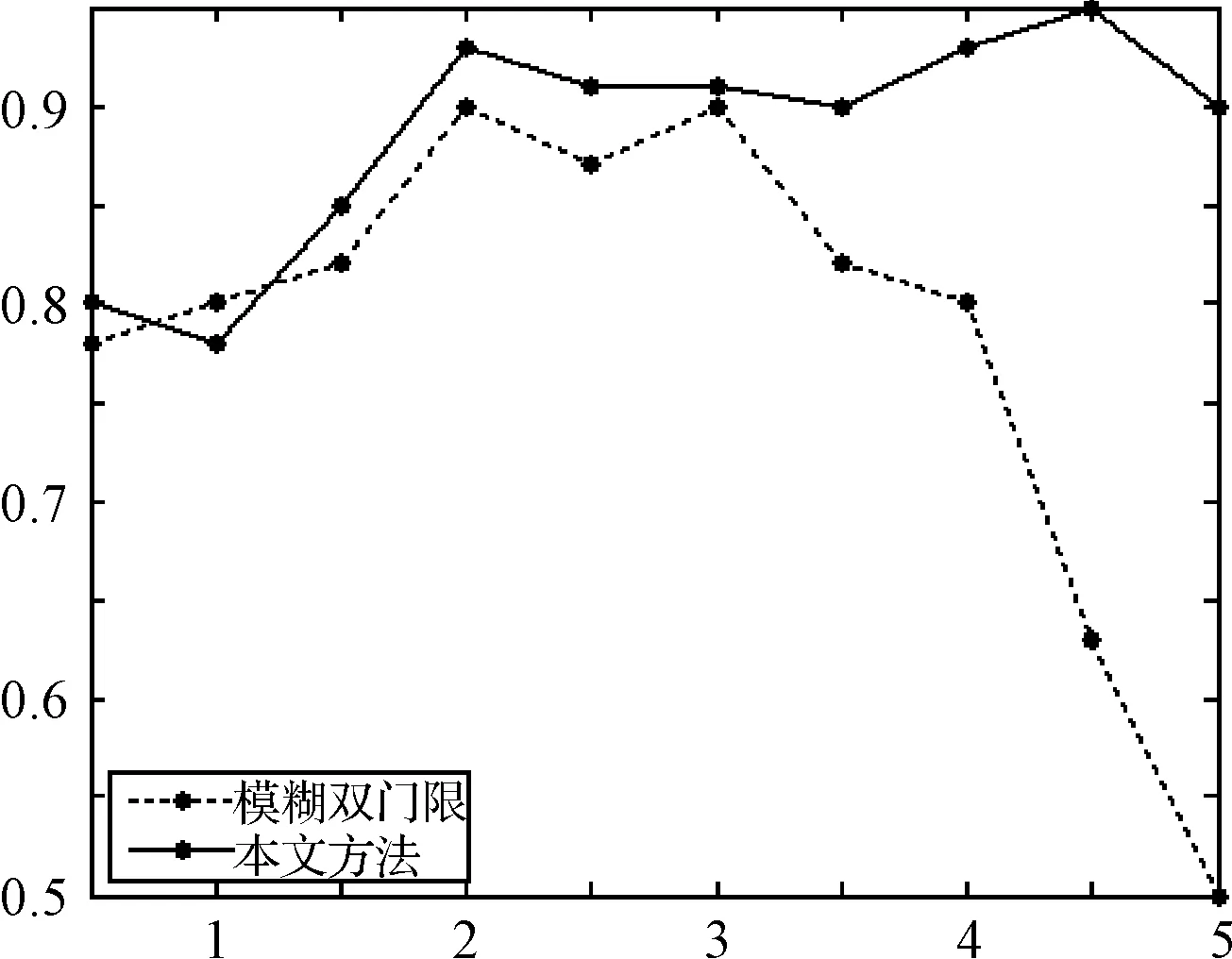
图5 目标2关联正确率与系统偏差倍数关系

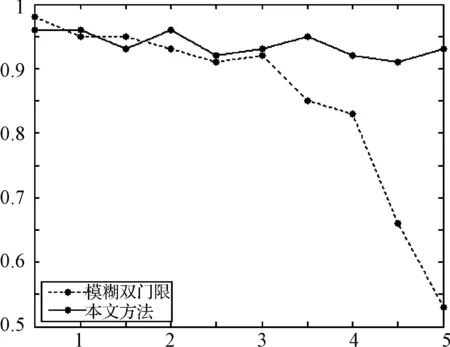
图6 目标3关联正确率与系统偏差倍数关系图

图7 目标4关联正确率与系统偏差倍数关系图

5 结语

本文针对航迹具有较大系统偏差无法通过传统方法进行有效关联的问题,提出一种基于目标拓扑参照图匹配的抗差关联方法,仿真结果表明当系统偏差为1～5倍随机误差时,该方法仍然能进行有效关联,明显优于传统方法,充分证明了该方法的有效性与鲁棒性。

[1] Singer R A, Stein J J. An optimal tracking filter for Proceessing sensor data of imprecisely determined origin in surveillance system[C]//Proceddings of the tenth IEEE Conference on Decision and Control. USA: Institute of Electrical and Eletronics Engineers,1971:171-175.

[2] Whang J H, Lee J G. Multiple Hypothesis Tracking for Maneuvering Tartets In Clutter Environment[C]//SICE’95, Sapporo,1995:1493-1498.

[3] 何友,等.多目标多传感器模糊双门限航迹相关算法[J].电子学报,1998(3):15-19.

[4] 王玥,王钺,王树刚,等.基于目标参照拓扑的模糊航迹关联方法[J].国防科技大学学报,2006,38(4):105-109.

[5] 杨哲,韩崇昭,等.基于目标之间拓扑信息的数据关联方法[J].系统仿真学报,2008,20(9):2357-2360.

[6] Shu Hong-ping. Research on Multirada Data Fusion Algorithm based on K-central Clustering[C]//IECT’2006, Cheng du Southwest Jiaotong Universty, September 28,2006:47-50.

[7] 夏学知,涂葵.多传感器数据融合并行处理技术[J].计算机应用,2005,25(8):1814-1817.

[8] Simper A. Correcting feneral band-to-band misregistrations[C]//Proc.IEEE ICIP’96,1996,2:597-600.

[9] Ton J, Jain A K. Registering landsat images by point matching[J]. IEEE Trans. Geosci. Remote Sensing,1989,27:642-651.

[10] 苏娟,林行刚,刘代志.一种基于结构特征边缘的多传感器图像配准方法[J].自动化学报,2009,35(3).

A Data Association Algorithm Based on Target Topologic Reference Graph

LI Ming

(No.1 Canglong North Road, Jiangxia Zone, Wuhan 430205)

In order to resolve the association problem affected by radar system bias, a new data asociation algorithm based on target topologic reference graph has been presented. Firstly, targets are clustered to reduce the complexity, and then through target topologic reference graph being used to match, it achieves the targets association. The simulation results show that the method has better accuracy and robusticity.

data association, system bias, clustering, match

2015年1月3日,

2015年2月27日 作者简介:李明,男,高级工程师,研究方向:船载指控系统。

TN957; TP274

10.3969/j.issn1672-9730.2015.07.027