雷达组网GMPHDF关键参数研究
丁海龙,赵温波
(解放军陆军军官学院, 合肥 230031)
·信号/数据处理·
雷达组网GMPHDF关键参数研究
丁海龙,赵温波
(解放军陆军军官学院, 合肥 230031)
高斯混合概率假设密度滤波具有严密的数学基础,适合跟踪弱信噪比多目标,但其目标分布协方差P和高斯元素裁剪门限T至今未有合理取值规则,影响了跟踪效果,且残差协方差S参与增益计算时需要对其进行逆计算,如果S为非正定,会导致计算发散。针对上述问题,通过概率统计方法推导了参数P和T的取值规则,通过Cholesky和QR分解,确定了参数S的计算规则。仿真比较分析表明:文中提出的目标分布协方差P、裁剪门限T和残差协方差S的计算规则用于雷达组网高斯混合概率假设密度滤波跟踪弱信噪比多目标时,能较高精度地跟踪到所有目标,且没有带来多余计算负担。
雷达组网;高斯混合概率假设密度滤波;参数
0 引 言
现代战争条件下,反辐射导弹、隐身目标、超低空突防和综合性电子干扰等装备广泛使用,使得雷达系统获得的目标回波能量大为减少,对目标的检测跟踪效果也大为降低,目标信息急剧减少,杂波信息却迅速增加,这种情况我们称之为雷达弱信噪比(Weak Signal to Noise Ratio, WSNR)目标检测跟踪[1]。雷达组网系统[2-3]为多源数据融合系统,一定程度上可以提高空域目标探测的空间/时间分辨率,但WSNR条件下,由于大量测量噪声和杂波信息的存在,弱信息目标很容易淹没在杂波虚警当中,当检测跟踪目标数未知的多个目标时,雷达检测到的数据并非就是目标信息,为了准确跟踪到目标,需要对目标数目和状态同时进行估计。传统的方法是将雷达测量信息与估计目标进行数据关联计算,数据关联会造成大量的计算量,给工程应用带来不便。概率假设密度滤波(Probability Hypothesis Density Filter, PHDF)[4-5]以随机有限集和贝叶斯滤波为其理论基础,借鉴贝叶斯单目标跟踪办法,将多目标状态和测量信息分别作为有限集来处理,避免了复杂的数据关联。高斯混合概率假设密度滤波(Gaussian Mixture PHDF, GMPHDF)[6-8]是PHDF的一种解析解实现形式,实现了PHDF的工程实际应用。然而,对于GMPHDF当中多目标方差P和裁剪门限T的选取,至今未提出合理的选取规则,仅凭经验进行选取,很容易增大跟踪误差,甚至造成跟踪失败,并且在计算滤波增益K时,需要求残差协方差的逆矩阵 ,如果S是非正定矩阵,会造成计算发散。本文通过数学分析,推导了P、T合理的选取规则,通过Cholesky和〗QR分解,解决了计算增益时的发散问题,并通过成功的雷达组网弱信噪比环境跟踪多目标仿真实验,验证了P、T选取的合理性和S计算增益的有效性,得到了很好的效果。
1 高斯混合概率假设密度滤波
GMPHDF的理论基础是随机有限集和贝叶斯滤波理论,它是在高斯条件下通过传播多目标随机有限集的一阶矩(概率假设密度)来近似后验分布,不考虑一阶矩以上的统计特性。其对应的迭代等式为
Dk+1|k(X)= ∫ps,k+1(ζ)fk+1|k(X|ζ)Dk(ζ)dζ+
∫βk+1|k(X|ζ)Dk(ζ)dζ+γk+1(X)
(1)
Dk+1(X)= [1-pD,k+1(X)]Dk+1|k(X)+

(2)
式中:X为目标状态的随机有限集;Z为测量值的随机有限集;ps,k+1(ζ)为k时刻状态为ζ的目标在当前k+1时刻存活的概率;fk+1|k(X|ζ)为状态转移概率密度;βk+1|k(X|ζ)为k时刻状态为ζ的目标在k+1时刻衍生的目标概率假设密度;γk+1(X)为k+1时刻新生目标概率假设密度;pD,k+1(X)为当前k+1时刻检测到目标状态X的概率;Lk+1(Z|X)为似然函数;κk+1(Z)为杂波随机有限集密度。
根据参考文献[6-8],GMPHDF滤波流程为

(3)


(4)

(5)

(6)
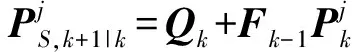
(7)
Dk+1|k(x)=Dγ,k+1|k(x)+Dβ,k+1|k(x)+
DS,k+1|k(x)
(8)
Dk+1(x)= (1-pD)Dk+1|k(x)+

(9)
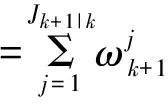
(10)

(11)

(12)
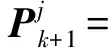
(13)

(14)
式(3)~式(5)分别为计算当前K+1时刻新生、衍生、存在目标的预测概率假设密度(Probability Hypothesis Density, PHD),式(6)、式(7)分别为计算衍生、存在目标的预测协方差矩阵,式(8)是新生、衍生、存在目标预测PHD的高斯混合,式(9)为计算更新后所有目标高斯元素的PHD,式(10)是被检测到的更新后高斯元素,式(11)~式(14)分别计算高斯元素PHD更新时用到的权值、状态值、协方差、增益。
滤波更新以后高斯元素会大量增加,导致过重的计算负担,需要对更新后的高斯元素进行裁剪与合并
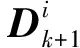
(15)
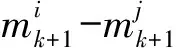
(16)
式中:T为PHD裁剪门限,U为合并门限。将不满足式(15)的高斯元素裁剪掉,不参与下一步计算,再将满足式(15)的高斯元素根据式(16)进行合并。
最后,提取权值大于0.5的元素为估计的目标数与状态。
2 高斯混合概率假设密度滤波参数研究
GMPHDF实现了PHDF的工程实践应用,但至今未给出GMPHDF裁剪处理当中门限T和新生、衍生目标分布协方差Pλ、Pβ具体取值规则,多是由经验进行取值。裁剪门限T取值过大会丢失有用信息,容易导致检测跟踪失败,取值过小会引入过量高斯元素(包括大量杂波高斯元素)参与下一步高斯元素合并计算,增大计算量,同时影响合并计算精度。GMPHDF各高斯元素服从高斯分布N(x;m,P),裁剪门限T用于与高斯元素PHD进行比较,因此,T具体取值决定于高斯元素的PHD,各元素PHD受分布协方差P影响。从这个意义上说,同样需要先确定各高斯元素分布协方差的取值。
2.1 确定目标分布方差取值规则
新生、衍生、存在目标的分布协方差Pλ、Pβ、PS描述高斯元素在均值附近的发散情况,以更准确地表示真实目标状态分布,由于存在目标分布协方差PS与过程噪声有关,取决于状态运动方程,下面主要是确定新生、衍生目标分布协方差Pλ、Pβ的选取规则。
式(14)中,参与计算状态更新增益的残差协方差为
(17)
2.2 确定裁剪门限T取值规则
新生、衍生目标方差Pλ、Pβ数量级与测量方差R相关,令其对应标准差为σ,则高斯元素m服从高斯分布N(x;m,σ2),其概率密度为
(18)
在高斯元素裁剪处理过程中,当高斯元素概率假设密度满足式(19)时,此元素就被裁剪,不参与下一步计算
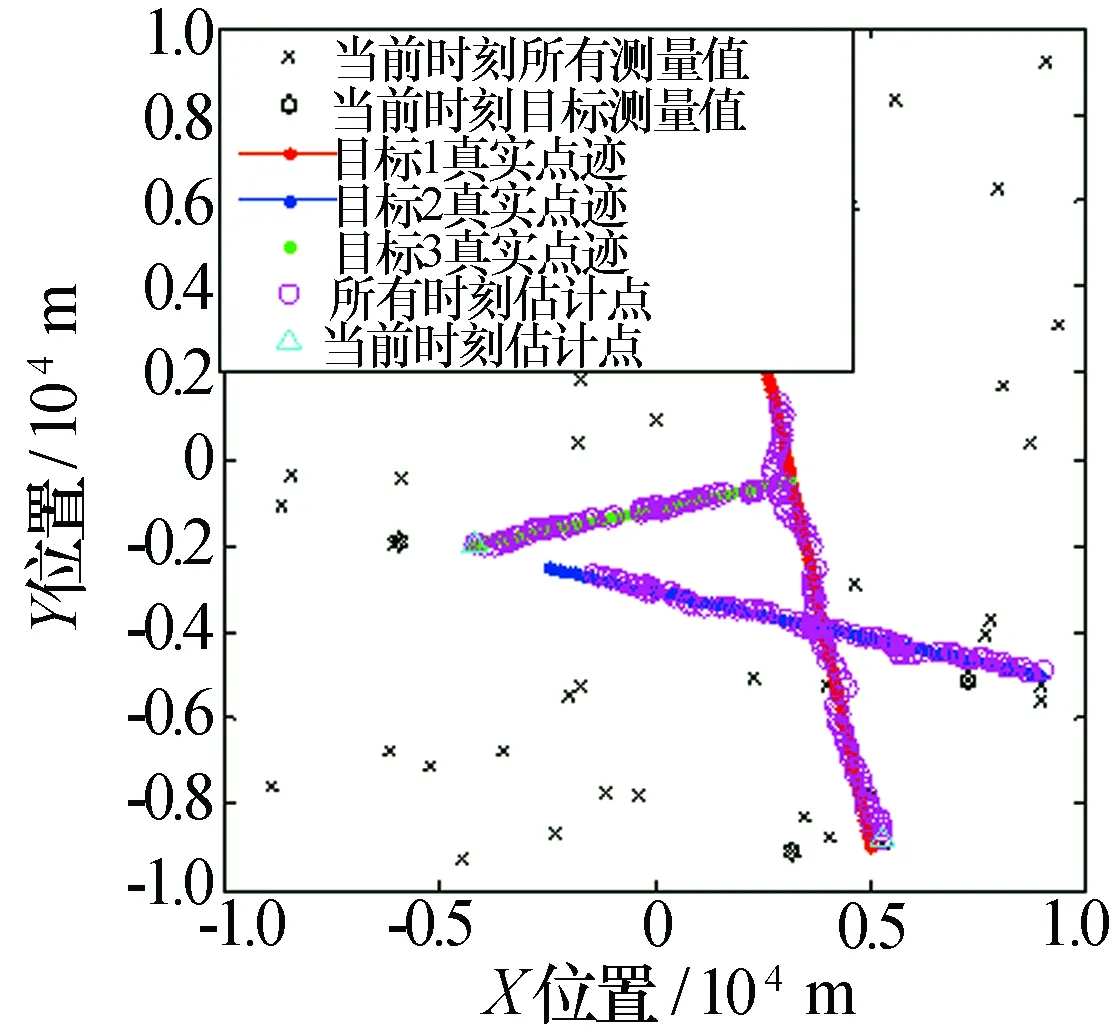
D=ωN(x;m,σ2) (19) 因此,门限T的取值要保证绝大多数(99.7%)有效高斯元素能参与计算。但门限T不能太小,否则会引入大量权值小的杂波元素,杂波元素参与下一步元素合并计算将影响其精度,并且增大计算量;T也不能太大,太大则造成只有少数高斯元素参与计算,丢失有用信息。式(18)概率密度f对应的概率函数可转换为标准正态分布的概率函数[10] (20) T取值要保证99.7%高斯元素参与计算,因此 (21) 查标准正态分布函数值表可得高斯元素状态x取值范围为x∈(m-3σ,m+3σ),如图1所示。 图1 高斯元素取值范围 将状态x取值范围代入式(19),因此可确定裁剪门限T取值规则 (22) 2.3 残差协方差分解计算 在式(14)、(17)中的残差协方差S如果是非正定矩阵,其参与增益K的计算时会导致计算发散,造成滤波失败,为解决这个问题,可对其进行Cholesky和QR分解,令 (23) 再对其进行QR分解 QrCholS=qr(CholS) (24) 则残差协方差可转换为 (25) 增益就可通过下式进行计算 (26) 由于QrCholS是经过QR分解得到的正定上三角矩阵,不会造成计算发散,因此,解决了计算增益K时的发散问题。 为了验证本文推导的正确性,采用Matlab软件仿真的方法来测试验证。仿真硬件环境为:Pentium(R) Dual-Core CPU,HP E5200,主频2.5 GHz,2.00 GB的内存。仿真场景如下:组网雷达两部,分别为雷达1和雷达2,雷达1的距离精度为130 m,方位角精度为0.3°,俯仰角精度为0.2°,配置位置为[118° 29° 120 m]T。雷达2的距离精度为90 m,方位角精度为0.4°,俯仰角精度为0.1°,配置位置为[117° 31° 20 m]T。融合中心的配置位置为[117° 30° 170 m]T。为了验证计算的简便性,特别假定两组网雷达对目标进行等间隔(1 s)探测,融合中心每秒能接收到一次探测数据,全程探测时间为100 s,所探测的目标处于强杂波环境,并且目标数量未知,探测目标全程飞行高度6 000 m不变,探测区域为二维区域[-105, 105]×[-105105],目标存活概率PS=0.99,存活目标服从线性高斯分布,状态转移矩阵和过程噪声方差分别为 (27) (28) 式中:时间间隔Δt=1s;过程噪声标准差σ=5m/s2。新生、衍生目标都服从泊松分布,其高斯混合形式分别为 (29) βk+1|k(x|ζ)=0.05N(x;ζ,Qβ) (30) Kk(z)=λcVu(z) (31) 在26s时目标1衍生出目标3,目标3做匀速直线运动,速度为V3=[-100 -20]T,滤波裁剪合并高斯元素过程中合并门限U=4,允许参与计算的最多高斯元素J=100。下面,分别对5种取值情况进行仿真比较,每种情况残差协方差S均应用本文的分解处理。跟踪开始时,将目标1、2作为新生目标处理,跟踪以后,跟踪点迹与目标真实点迹误差用最优子分配(Optimal Subpattern Assignment, OSPA)距离来度量,OSPA距离计算参考文献[11-12],实验中距离上限设置为200 m。为了克服随机因素影响,进行100次仿真统计计算。 (1)根据本文取值规则,新生、衍生目标分布协方差取值与融合中心测量噪声虚拟方差R一致,裁剪门限T根据式(22)计算 Pγ=diag([105, 105, 25, 25]T) (32) Pβ=diag([105, 105, 400, 400]T) (33) T=10-7 (34) 跟踪效果图如图2、图3所示。 图2 GMPHDF跟踪、目标真实点迹与当前时刻测量值 图2是跟踪点迹与真实点迹的OSPA距离图,OSPA距离均方根为25m,全程计算耗时89.18s。从图2可以看出,在第26s从目标1衍生出目标3,在强杂波环境下,选用本文参数取值规则的GMPHDF跟踪多目标,经过一定点迹信息积累以后,能跟踪到继续存在目标和新衍生目标,从图3可以看出,本文GMPHDF跟踪误差较小,且在一定时间内,跟踪误差方差(OSPA均方根)随时间增长越来越小,适合于工程实际应用。 图3 X、Y方向GMPHDF跟踪点迹与测量值 (2)与条件(1)相比,只增大裁剪门限T,其他条件相同:T=10-6。 与跟踪条件(1)相比,当裁剪门限T取值大于本文取值规则确定的值时,从图4可以看出,GMPHDF不能跟踪到继续存在目标和新衍生目标,跟踪失败。 图4 GMPHDF跟踪、目标真实点迹与当前时刻测量值 (3)只减小裁剪门限T,其他条件与(1)相同:T=10-8。 从图5可以看出,与条件(1)相比,当裁剪门限T减小时,同样能跟踪到所有目标,但由图6可知,由于裁剪掉的高斯元素变少,进入裁剪以后滤波计算的高速元素增加,其中,包括大量杂波元素,增大了计算负担,计算耗时与条件(1)的89.18s相比,增加到185.61s,并且影响了计算精度,图6中OSPA距离均方根增加到30m,跟踪误差方差并未像条件(1)随时间增加而减小。其结果与本文分析一致。 图5 GMPHDF跟踪、目标真实点迹与当前时刻测量值 图6 跟踪点迹与真实目标点迹OSPA距离 (4)只增大新生、衍生目标分布协方差Pγ、Pβ,其他条件与(1)相同 Pγ=diag([106, 106, 25,25]T) (35) Pβ=diag([106, 106, 400, 400]T) (36) 此种条件下,同样导致跟踪失败,其跟踪效果图如图4、图5所示。 (5)只减小新生、衍生目标分布协方差 ,其他条件与(1)相同 Pγ=diag([104, 104, 25,25]T) (37) Pβ=diag([104, 104, 400, 400]T) (38) 从图7可以看出,目标分布方差减小时,经过一定点迹信息积累以后,只能跟踪到继续存在目标,不能检测跟踪到新衍生目标。 图7 GMPHDF跟踪、目标真实点迹与当前时刻测量值 针对GMPHDF弱信噪比环境下跟踪多目标时,目标分布方差和裁剪门限按经验选取,影响跟踪效果,以及残差协方差参与增益计算容易导致计算发散问题,从概率统计角度确定了分布方差和裁剪门限选值规则,通过Cholesky和QR分解保证了残差协方差正定性,避免了取逆计算时发散问题。5种情况仿真对比实验表明,本文确定的参数方差P、裁剪门限T、残差协方差S计算规则用于GMPHDF跟踪弱信噪比多目标时,能成功跟踪到新生、衍生和存在目标,跟踪精度较高,OSPA距离均方根误差25 m,且均方根误差一定时间内随滤波步数增长,越来越小。因此,本文确定的GMPHDF参数取值规则科学合理,适用于跟踪弱信噪比多目标。 [1] 战立晓,汤子跃,朱振波. 雷达微弱目标检测前跟踪算法综述[J]. 现代雷达, 2013, 35(4): 45-52,57. Zhan Lixiao, Tang Ziyue, Zhu Zhenbo. An overview on track-before-detect algorithms for radar weak targets[J]. Modern Radar,2013,35(4): 45-52,57. [2] 王文星,印士波,张 帜,等. 雷达组网应用的体系结构研究[J]. 现代雷达, 2014,36(5): 26-30. Wang Wenxing, Yin Shibo, Zhang Zhi,et al. A study on radar network application architecture[J]. Modern Radar, 2014, 36(5): 26-30. [3] 杨跃轮,李洪梅. 分布式干扰下雷达组网探测效能分析[J]. 指挥控制与仿真, 2012,34(3): 41-43,66. Yang Yuelun, Li Hongmei. Analysis of radar nets' operational effectiveness on the condition of distributed jammers[J]. Command Control & Simulation,2012,34(3): 41-43,66. [4] Mahler R P S. Multitarget bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178. [5] 吴 伟, 黄 冶. 目标起始和维持规则辅助的SMC-PHD滤波方法[J]. 现代雷达, 2013,35(9): 24-29,35. Wu Wei, Huang Ye. An improved SMC-PHD algorithm assisted by target initiation and continuity rules[J]. Modern Radar, 2013, 35(9): 24-29,35. [6] Vo B N, Ma W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104. [7] Li W L, Jia Y M. Gaussian mixture PHD filter for jump Markov models based on best-fitting Gaussian approximation[J]. Signal Processing, 2011, 91(4): 1036-1042. [8] 刘宗香,谢维信,王 品,等. 一种具有信息保持能力的GM-PHD滤波器[J]. 电子学报, 2013, 41(8): 1603-1608. Liu Zongxiang, Xie Weixin,Wang Pin, et al. A gaussian mixture PHD filter with the capability of information hold[J]. Acta Electronica Sinica, 2013, 41(8): 1603-1608. [9] 赵温波,都基焱. 组网雷达噪声惯性坐标系误差统计特性研究[J]. 炮兵学院学报, 2010(5): 91-95. Zhao Wenbo, Du Jiyan. Study on statistical properties of radar network noise in inertial coordinate system[J]. Journal of Artillery Academy, 2010(5): 91-95. [10] 龙永红. 概率论与数理统计[M]. 北京:高等教育出版社, 2000. Long Yonghong. Probability theory and mathematical statistics[M]. Beijing: Higher Education Press, 2000. [11] Hoffman J R, Mahler R P S. Multitarget miss distance via optimal assignment[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 2004, 34(3): 327-336. [12] Schuhmacher D, Vo B T, Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008,56(8): 3447-3457. 丁海龙 男,1987年生,硕士研究生。研究方向为雷达数据处理。 赵温波 男,1972年生,副教授,硕士生导师。研究方向为统计信号处理。 A Study on Some Key Parameters of GMPHDF in Radar Network DING Hailong,ZHAO Wenbo (Amy Officer Academy of PLA, Hefei 230031, China) Gaussian mixture probability hypothesis density filter(PHDF), which is suitable for tracking weak signal to noise ratio(WSNR) multi-target, has rigorous mathematical foundation. But there is no reasonable calculation rules about distribution covariancePand truncation thresholdTof Gaussian elements in PHDF as yet, which bring bad influence to PHDF. Because the residual covarianceSwill be inverse calculated when it is involved in the gain calculation. IfSis non-positive definite, it would lead to divergence calculation. Probability statistics derivation is used to determine thePandTcalculation rules. Cholesky and QR decomposition is used to solve theScalculation problem. The simulation comparison demonstrates that PHDF in radar network, using the proposed calculation rules ofP,TandS, can precisely track WSNR multi-target, containing exist, birth and spawn targets, and bring no extra calculation burden. radar network; Gaussian mixture probability hypothesis density filter; parameter 10. 16592/ j. cnki. 1004-7859. 2015. 09. 011 国家自然科学基金资助项目(61273001);安徽省自然科学基金资助项目(11040606M130) 丁海龙 Email:656797226@qq.com 2015-04-26 2015-05-27 TN953 A 1004-7859(2015)08-0044-06




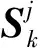

3 仿真实验与分析
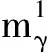






4 结束语

