步进频波形优化设计及处理技术
颜志升
(南京电子技术研究所, 南京 210039)
·信号/数据处理·
步进频波形优化设计及处理技术
颜志升
(南京电子技术研究所, 南京 210039)
为增大步进频信号对多普勒效应的容忍度,文中对波形参数进行了优化设计。通过研究认为,对多普勒效应的容忍范围与脉冲重复周期之间存在强耦合关系,为增大容忍范围需要尽可能减小脉冲重复周期。为解决因减小重复周期而可能带来的距离模糊问题,提出了在频率上对发射端和接收端进行异步设置的处理技术,并且为了避免雷达作用范围内的盲区,提出了根据目标所在距离自适应设计信号波形参数的方法,此方法与处理技术特别适用于远程警戒雷达。
步进频;多普勒容忍度;波形参数设计;自适应波形
0 引 言
现代战争对雷达的要求不断提高,不仅要能探测和跟踪目标,而且在特定情况下要能够对目标进行分类与识别,在此背景下雷达系统的宽带处理能力非常关键。步进频信号是一种重要的宽带信号,它有两个显著的优点:(1)能够降低系统成本,因为信号的瞬时带宽较小,可以使用窄带器件搭建宽带的雷达系统;(2)可以有效提高雷达抗干扰能力,从频域上看,只有小范围内的干扰可实时地进入接收机,而在直接宽带系统中,在信号带宽内的干扰都能实时进入接收机。
对步进频信号而言,比较实用的处理方法包括:包络合成[1]、时域合成[2]、频域合成[3]。对此三类方法的对比研究比较多,比如文献[4-5],在此不再赘述。本文的研究只针对于频域合成的方法。
步进频信号是一种对多普勒效应非常敏感的信号。在雷达作用于运动目标时,通常先估计目标的速度,再根据速度的估计值对信号进行补偿(消除因速度引起的频率和相位影响),最后,再合成宽带信号。对目标速度估计是步进频的难点,有很多文献研究了此问题[6-11],本文对此不展开讨论。
现有文献对频域合成方法原理的研究一般限于静止目标所引起的回波信号[3-4,11],也可以认为是运动目标引起的回波经过精确补偿后的结果。当然,这只是速度估计非常准确的理想情况,但是在实际工程中速度估值存在不可避免的误差,所以,即使经过速度补偿,目标回波仍存在速度余量。在含有速度余量的情况下,最终合成的高分辨率一维距离像会出现栅瓣,这给目标分类与识别工作带来了非常严重的危害。因此,研究这种“非理想”情形更为实用。
本文的重点在于研究步进频信号对多普勒效应敏感的机理,分析在频域合成方法中如何提高步进频雷达对多普勒效应的容忍度,释放精确测速的压力;并且,本文研究了相应的信号波形设计与处理方法,使步进频信号能更好地应用于远程警戒雷达。
1 原理与方法
1.1 步进频信号的基本原理
下面假设步进频信号共含有N个脉冲,用f0表示脉冲串的中心频率,用Δf表示相邻脉冲的载频步进量,则不同脉冲的载频为

(1)
发射信号可表示为
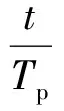
(2)
式中:rect()为矩形函数;Tp为脉冲宽度;K=B/Tp为扫频斜率;B表示单个脉冲内部的扫频范围,在此规定B=Δf。为简便起见,在窄带脉冲信号中忽略多普勒效应对调制的影响,认为多普勒效应仅对载频起影响,所以回波信号可表示为

(t-τn)+jπK(t-τn)2)
(3)
式中:τn=τ0+(n-1)2vTr/c为不同脉冲的回波信号的延时,τ0为初始延时,v为目标速度,c为光速,Tr为脉冲重复周期;fd=2vf0/c表示回波信号的多普勒频移。经过混频后上述回波转换成基带信号

exp(j2πfd(t-τn)+jπK(t-τn)2)
(4)
在理想情况下,将回波中速度的影响完全消除,此时基带信号为
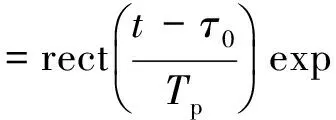
jπK(t-τ0)2)
(5)
在频域合成宽带信号可分为以下三个步骤:
(1)在频域完成匹配滤波
将式(5)所示基带信号通过下述匹配滤波器
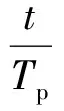
(6)
匹配滤波器的输出信号在频域表示为
So,n(f)=|S(f)|2exp(-j2πfc,nτ0-j2πfτ0)
(7)
式中:S(f)为发射波形去载频后的频域表示,可以近似认为
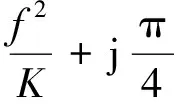
(8)
(2)拼接相位谱
结合式(1)和式(7)可知,在相同频率值上,相邻脉冲的滤波结果的相位差为exp(-j2πΔfτ0);相位谱中的斜率为-2πτ0,对具体某个脉冲而言在频率上相差Δf的两个位置的相位差为exp(-j2πΔfτ0),所以有
(9)
式(9)表明,将相邻两个脉冲的频谱在频率轴上平移Δf后,此两个信号在频率重合位置上的相位相同,所以,通过移频后求和可以将不同脉冲的相位谱拼接成一条直线。
(3)补偿幅度谱
在上述同相位相加后,两个脉冲交叠部分的幅度跟其他位置的幅值不同,通过幅度补偿可以使相加结果的幅度谱变为平整的矩形函数。通常的方法是测量在单散射点情况下所有脉冲的幅度谱之和,用它的倒数对实际回波信号的幅度谱进行补偿。
经过上述匹配滤波、移频求和且幅度补偿后,所得结果的相位谱是一条直线,并且幅度谱是矩形函数,所以,最终结果等效于宽带的线性调频信号经过匹配滤波之后的结果。在此基础上再经过加窗处理和逆傅里叶变换,最终得到高分辨率的一维距离像。
1.2 增大对多普勒效应容忍度的方法
在非理想情况下,回波信号中速度的影响不能完全消除。此时,式(4)在频域中可表示为
Si,n(f)= S(f-Δfd)·exp(-j2πfτn)·
exp(-j2πfc,nτn)
(10)
式中:Δfd=-2Δvf0/c为多普勒频移的余量;Δv为速度余量,并且重新定义τn=τ0+2(n-1)ΔvTr/c,在匹配滤波后的结果为
So,n(f)= |S(f-Δfd)S(f)|·exp(-j2πfτ0-


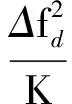
(11)
跟式(7)相比,式(11)中幅度谱乘积会产生错位(在多普勒频移余量较小时不易观察),并且相位随脉冲编号的变化是由速度余量而引出的,它会导致单个脉冲相位谱的斜率不再等于-2πτ0,而是随脉冲编号发生变化,图1表示了当存在多普勒频移的余量时,回波的幅度谱与相位谱的变化规律。

图1 多普勒频移对脉冲串信号频谱影响示意图
式(11)中第二行相位因子可重新整理为
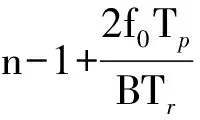
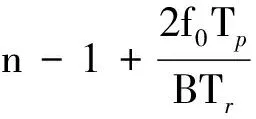
1.3 发射/接收频率异步处理技术
在通常的脉冲多普勒雷达中,雷达发射和接收交替进行,设发射/接收周期为Tr,如果两个目标所在距离上相差cTr/2或其整数倍,由它们所引起的回波信号有可能同时到达接收机,即回波信号混叠在一起,造成距离模糊。所以,将重复周期Tr尽可能拉长,就可以避免距离上的模糊,这对雷达信号处理非常有利。但是,如前所述,步进频的重复周期Tr与它对多普勒效应的容忍度呈现此消彼长的规律,为了增大对多普勒效应的容忍度,必须适当减小重复周期。
在步进频雷达中,虽然这些位于不同距离上的目标所引起的回波信号同时到达接收机,但是它们的频率不相同,所以通过合理配置接收端的本振频率,再结合在基带上的低通滤波器和匹配滤波器,将距离差为cTr/2或其整数倍的目标进行分离。
假设我们感兴趣的目标信号在时域发生5次模糊,即第1个脉冲被发射出去后,这个目标引起的回波在第5个发射-接收周期后才返回至雷达,为接收该目标的回波,可以将接收端的本振信号按图2a)设计,在第6个脉冲发射完毕之后,接收端的频点设置为f1。虽然此时也有其他距离上的目标回波信号正好到达接收机,且在时域刚好完全混叠在一起,但是这些无意目标的回波信号的频率只能为f2、f3、f4等,所以将接收端本振设置为f1,则其他频率的回波信号会被混频器之后的低通滤波器和匹配滤波器滤除,如图2b)所示,这样消除了我们感兴趣的目标与其他无意目标之间的模糊。

图2 发射和接收在频率上异步工作示意图
1.4 自适应调整波形参数的方法
假设发射宽度固定为Rt,接收宽度可以调整,变化范围的上限和下限已给出,Rr∈[Rr1,Rr2],现在要求距离为R处的目标所引起的回波信号能被完整的接收(即回波信号的前沿、后沿均能顺利地进入接收机),则要求
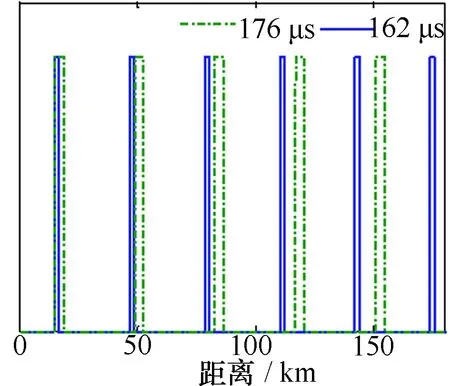
Rt (12) 式中:n=⎣R/(Rt+Rr)」表示目标距离相对于发射-接收总宽度的倍数,或者说目标回波信号在距离上的折叠次数。将式(12)进行变形得到 n(Rt+Rr)+Rt (13) 从式(13)可看出,如果已知目标距离,可以通过调整接收时间宽度的方法,使该目标的回波信号被完整接收。 在式(13)中n跟Rr有关,且Rr发生微调时对应的n值可能不变(即折叠的次数相同)。在确定Rr和n值之后,满足式(13)的距离通常是一个取值范围,如图3所示,在两条斜率相同的直线中间的距离范围内,目标回波信号都能被完整接收。 由于接收时间宽度可以调节,所以图3中的直线的斜率可以被调整,若增大接收时间宽度,则直线的斜率变大,如图中虚线所示。 图3 雷达可观测距离与折叠次数的关系示意图 为了排除观测盲区,必须使雷达可作用范围内的距离R均能被“夹住”在某两条直线中,即要求自变量为n时对应的最大距离不小于自变量为(n+1)时的最小距离,所以有 n(Rt+Rr2)+Rr2≥(n+1)(Rt+Rr1)+Rt⟹ (14) 也可以对式(12)进行更严格的约束,比如 2Rt (15) 相应地,式 (14)变为 n(Rt+Rr2)+Rr2-Rt≥(n+1)(Rt+Rr1)+2Rt⟹ (16) 综上所述,在已知目标距离的前提下,兼顾Rr取值范围与排除距离维盲区的限制条件,可以先确定n值,再根据Rr和n的关系从Rr取值范围内选择具体数值。 2.1 比较不同重复周期给多普勒容忍度带来的影响 在此仿真中,载频为1GHz,脉冲宽度为50μs,频率步进量为20MHz,脉冲内部带宽为20MHz,脉冲个数为4个,原始采样率为80MHz,经过抽取器后采样率降为40MHz,模拟目标的距离为200km,脉冲周期分为246μs和2.5ms两种情况,仿真结果如图4所示。 图4 在两种重复周期下的一维像对比 由图4可以看出,若保证栅瓣电平低于-30dB,当Tr=2.5ms时,对速度余量的容忍范围仅为1m/s;当Tr=246μs时,则对速度余量的容忍范围可增大1个量级。 2.2 自适应波形设计例子 在此仿真中,设定发射时宽为50μs,接收时宽调整范围为100μs~260μs。若目标距离为80km,经过计算后可设置接收时间162μs,相应的n=2;若目标距离为120km,则可设置接收时间176μs,相应的n=3。 此外,目标信号能够按式(15)被完整接收的距离是多个离散的区域,只不过折叠次数不同,如图5所示,所以按照前述方法设计的信号波形,即使我们感兴趣的目标位于不同距离上时,信号的重复周期有可能相同,图5中的矩形表示该范围内的目标所引起的回波均能按式(15)被完整接收。虽然如此,它不会引起距离上的模糊,因为前述发射/接收频率异步处理技术能将不同距离上的目标信号行分离。 图5 两种波形参数对应的可被完整接收的距离范围 本文针对在频域合成宽带信号的方法研究了步进频对多普勒频移敏感的机理,讨论了通过减小脉冲重复周期以增大对多普勒效应容忍度的方法。本文的仿真结果证实了在其他参数不变的前提下,一维像中栅瓣相对于主瓣的高低与信号重复周期的对应关系:当速度余差一定时,如果信号重复周期越小,则栅瓣越低。 在已知目标距离的前提下,通过在频率上将发射和接收分开设置,解决了距离模糊问题。在减小脉冲重复周期后,有可能带来距离上的盲区。本文讨论了根据目标距离自适应调整脉冲重复周期的方法,使得我们感兴趣的目标所引起的回波均能完整地被接收。 本文讨论的方法需要预先知道目标的距离,或者大体知道目标的距离,它的应用受到一定限制,只适用于先搜索后跟踪的雷达:通过搜索知道目标的距离,在跟踪阶段用步进频合成高分辩率一维像。 [1] 龙 腾, 毛二可, 何佩琨. 调频步进雷达信号分析与处理[J]. 电子学报, 1998, 26(12): 84-88.LongTeng,MaoErke,HePeikun.Analysisandprocessingofmodulatedfrequencysteppedradarsignal[J].ActaElectronicaSigica,1998, 26(12): 84-88. [2]LordRT,InggsMR.Highrangeresolutionradarusingnarrowbandlinearchirpsoffsetinfrequency[C]//IEEESouthAfricanSymposiumonCommunicationsandSignalProcessing.[S.l.]:IEEEPress, 1997: 9-12. [3] Wilkinson A J, Lord R T, Inggs M R. Stepped-frequency processing by reconstruction of target reflectivity spectrum[C]// IEEE South African Symposium on Communications and Signal Processing.[S.l.]: IEEE Press, 1998: 101-104. [4] Lord R T. Aspects of stepped-frequency processing for low-frequency SAR systems[D]. Cape Town: University of Cape Town, 2000. [5] 丁海林, 李亚超, 高昭昭,等. 线性调频步进信号的三种合成方法的对比与分析[J]. 火控雷达技术, 2007, 36(4): 10-16, 30. Ding Hailin, Li Yachao, Gao Zhaozhao, et al. Comparison and analysis to three synthesis methods of linear FM stepped-frequency signal[J]. Fire Control Radar Technology, 2007, 36(4): 10-16, 30. [6] 毛二可, 龙 腾, 韩月秋. 频率步进雷达数字信号处理[J]. 航空学报, 2001, 22(增刊): 17-25. Mao Erke, Long Teng, Han Yueqiu. Digital signal processing of stepped frequency radar[J]. Acta Aeronautica Et Astronautica Sinica, 2001, 22(Sup): 17-25. [7] Abatzoglou T J, Gheen G O. Range, radial velocity, and acceleration MLE using radar LFM pulse train[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1070-1083. [8] 牛 涛, 陈卫东. 脉冲步进频率雷达的一种运动补偿新方法[J]. 中国科学技术大学学报, 2005, 35(2): 161-166. Niu Tao, Chen Weidong. A new method of motion compensation for pulse stepped-frequency radars[J]. Journal of University of Science and Technology of China, 2005, 35(2): 161-166. [9] 王桂丽, 李兴国. 频率步进和脉冲多普勒复合测速研究[J]. 红外与毫米波学报, 2008, 27(3): 190-192, 201. Wang Guili, Li Xingguo. Compound approach of measuring velocity based on step-frequency and pulse Doppler system[J]. Journal of Infrared and Millimeter Waves, 2008, 27(3): 190-192, 201. [10] 张宏伟, 俞静一, 徐 阳, 等. 基于α-β滤波的频率步进导引头运动补偿算法研究[J]. 现代雷达, 2013, 35(7): 28-30. Zhang Hongwei, Yu Jingyi, Xu Yang, et al. A study on stepped-frequency seeker motion compensate algorithm based on α-β filter[J]. Modern Radar, 2013, 35(7): 28-30. [11] 陈 涛, 杨 飞. 一种频域合成宽带雷达信号的快速算法[J]. 现代雷达, 2013, 35(4): 35-38, 44. Chen Tao, Yang Fei. A fast algorithm for frequency domain synthetic wideband radar signal[J]. Modern Radar, 2013, 35(4): 35-38, 44. 颜志升 男,1984年生,工程师。研究方向为雷达系统工程。 Optimized Design of the Stepped-frequency Signal Waveform and its Processing Technology YAN Zhisheng (Nanjing Research Institute of Electronics Technology, Nanjing 210039, China) The optimal design of the stepped-frequency waveform for increasing its Doppler tolerance is focused on. It is concluded that the Doppler tolerance is tightly coupled with the pulse repeating interval (PRI), so it is favorable to decrease the PRI in order to increase the tolerable Doppler shifting. It rearranges transmitting and receiving in frequency for resolving the possible range ambiguity, also it proposes adaptively tuning the waveform parameters according to the target location for avoiding the blind zones within the detectable range. The suggested design and technology can be applied to long-distance guarding radar especially. stepped-frequency; Doppler tolerance; waveform design; adaptive waveform 10.16592/ j.cnki.1004-7859.2015.09.010 颜志升 Email:zhishen_yan@qq.com 2015-04-18 2015-01-20 TN A 1004-7859(2015)09-0040-04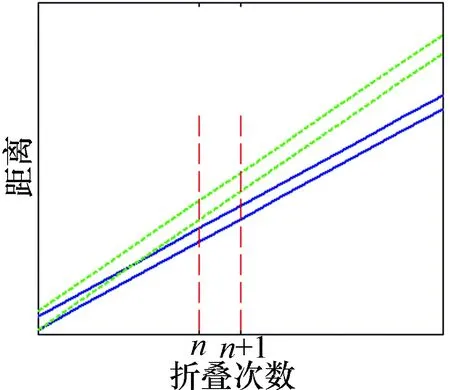

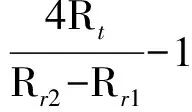
2 数值仿真

3 结束语

