机载双天线高低频InSAR系统设计

武 楠，何东元，胡学成，林幼权

(南京电子技术研究所， 南京 210039)



·总体工程·

机载双天线高低频InSAR系统设计

武 楠，何东元，胡学成，林幼权

(南京电子技术研究所， 南京 210039)

介绍了机载干涉合成孔径雷达(InSAR)测高原理，建立了机载InSAR系统模型并推导回波信号接收和处理流程所涉及的公式，剖析机载InSAR系统测高的全部误差源。对比高、低频段刚性基线和非刚性基线两种配置情况下机载InSAR系统测高误差来源的异同。在满足一定分辨率和测高精度的要求下，优选系统的基线形式和长度，通过计算分析了各种误差源对测高精度的影响。最后，计算了成像信噪比、测高灵敏度和高程精度等指标，其结论可以作为机载InSAR系统设计的有益参考。

机载雷达；干涉合成孔径雷达；基线；系统设计；数字高程模型

0 引 言

机载干涉合成孔径雷达(InSAR)利用垂直航向的分布式天线结构可以在全天时、全天候和单航过条件下较容易地获得大幅宽、高空间分辨率、高垂直精度的数字高程模型(DEM)。其空间分辨率主要由信号带宽和天线方位向长度决定，而垂直高程精度由斜距精度、平台高度精度、绝对干涉相位精度、基线长度精度和基线倾角精度等五个主要因素制约。

国际上先进的机载InSAR系统绝大多数是双天线系统，与机载单天线InSAR系统及星载SAR系统相比，机载双天线InSAR系统能够避免重复轨道干涉模式中存在的时间去相干问题，在地形制图方面有着相当大的优势。机载双天线InSAR系统通常有三种形式：(1)两副天线直接安装在载机机身上或在飞机机腹下的天线罩内，受飞机机身宽度的限制，基线长度较短，如日本的Ku波段机载InSAR天线安装在从机舱伸出的钢板两端，基线长度为1 m[1]。(2)改造部分飞机机体，引入一根较长的刚性杆结构，如德国机载AeS-1 InSAR将一根长2 m多的金属管横穿过载机机身，将用于干涉测高的天线固定在金属管的两端，基线长度非常稳定，且可在地面预先用经纬仪测量，飞行中基线长度随温度的变化通过记录刚性杆不同部位的温度来进行补偿[2]。(3)两副天线以吊舱的形式分别安装在机翼顶端，且由机翼形成一段非刚性基线结构，如美国机载GeoSAR P波段InSAR系统，用于干涉测量的P波段天线安装在“湾流Ⅱ”飞机翼尖的吊舱内，基线长度约为20 m，两个天线相位中心之间存在随机翼震颤而引起的相对变化，因而同时安装有光学基线测量设备对干涉基线进行实时测量[3]。

本文介绍了机载InSAR测高原理，建立了机载InSAR系统模型并推导回波信号接收和处理流程所涉及的公式，剖析机载InSAR系统测高的全部测高误差源。

1 InSAR测高原理和回波信号模型

机载InSAR成像几何如图1所示。该InSAR系统有分置的两副天线，既可以“一发双收”模式工作，也可以分时交替发射和接收，即“乒乓”模式工作。

图1 机载双天线InSAR成像几何关系

场景中P点地表高度h可以由简单的几何关系获得[4]

h=H-r1cosθ=H-r1·

(1)

(2)

式中：H为飞机平台上天线1相位中心的高度；θ为天线1下视角；B为天线1和天线2之间的基线长度；β为基线倾角(即基线与场景水平面的夹角)；r1为天线1到场景散射点P的斜距。在“一发双收”的工作模式下，天线1和天线2到场景散射点的斜距差Δ=r1-r2≈-λφ/2π，在“乒乓”模式下Δ≈-λφ/4π，其中φ为绝对干涉相位。

InSAR系统模型框图如图2 所示。在图2a)中，信号发射时，时分开关切换到发射支路，信号形成产生发射信号，上变频后经过发射支路和天线1辐射出去；接收时，时分开关切换到接收支路1，回波信号1由天线1接收，叠加噪声1经过接收支路1，再经下变频和AD采样，获得接收信号1；同时回波信号2由天线2接收，叠加噪声2经过接收支路2，再经下变频和AD采样，获得接收信号2。在图2b)中，雷达的两个发射和接收支路分时工作，信号交替发射和接收。

图2 InSAR系统模型框图

1.1 “一发双收”模式InSAR信号模型

设定雷达发射信号为标准的线性调频信号。在图2a)中,天线1接收的射频信号[5]为

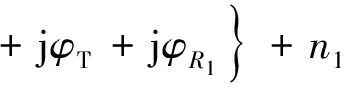
(3)

天线1和天线2接收通道本振信号均由一路本振信号功分而来，可以表示为

soscr_i(t)=exp[j2πfct+jφi0+jnφ(t+τi)]

i=1,2

(4)

式中：τi为电磁波传输延迟；i=1,2分别表示天线1和天线2的接收支路本振编号。

混频后，由于τi为毫秒量级甚至更小，使得nφ(t)-nφ(t+τi)≈0。因此，天线1接收的基带信号为

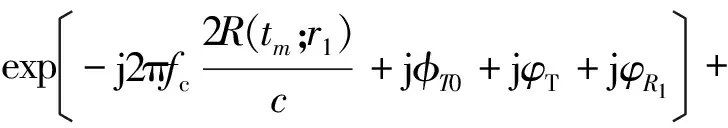
n1(t)

(5)

经过成像处理后，信号为

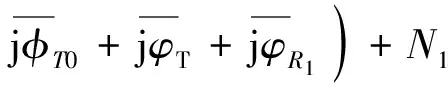
(6)

同样的推导过程，天线2获得的SAR图像为

N2(t)

(7)

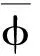
对上面的两式进行干涉处理，提取干涉相位为

(8)

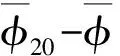
1.2 “乒乓”模式InSAR信号模型

在图2b)中，收发通道1成像处理结果为

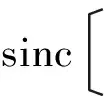
(9)

收发通道2成像处理结果为

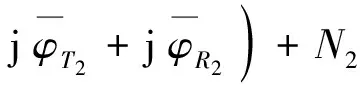
(10)

同样对式(9)和式(10)进行干涉处理，提取干涉相位为

(11)

2 InSAR测高误差源分析

天线1斜距r1、平台高度H、绝对干涉相位φ、基线长度B和基线倾角β的测量误差都会产生高程测量误差，且考虑到距离向地形坡度角α引起的高度误差∂h=∂y·tanα，InSAR高程测量误差共有5个，其解析表达式[4]如下：

1) 斜距测量误差导致的测高误差：

∂hr1=cosθ·∂r1

(12)

∂hr1由雷达测距误差引入，主要包括通道路径延迟、定时误差和定时抖动等，除定时抖动随机误差以外，可看作一项系统误差，因此可通过外定标消除绝大部分误差；

2) 平台高度测量误差导致的测高误差

∂hH=∂H

(13)

∂hH由惯导测量平台高度误差引入，由于机载条件下飞行高度不断变化，该项误差不再是一项系统误差；

3) 相位误差导致的测高误差

(14)

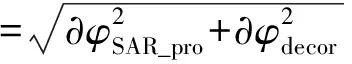
γ=γthermalγgeomγtemporalγvolumeγDopplerγcoreg

(15)

其中，热噪声相干性为

(16)

式中：SNR1为天线1获得的单视复图像信噪比，SNR2为天线2获得的单视复图像信噪比。

空间相干性为

γgeom=(B⊥C-B⊥)/B⊥C

(17)

式中：垂直雷达视线基线分量B⊥=Bcos(θ-β)，一发双收模式临界基线B⊥C=2Δfrr1λtan(θ-α)/c，“乒乓”模式B⊥C=Δfrr1λtan(θ-α)/c；Δfr为发射信号带宽。

时间相干性(双航过情况下)为

(18)

式中：σy和σz分别表示垂直航向水平和垂直方向运动的均方根，如果雷达进行单航过地形高度测量则γtempoal≈1。

体散射相干系数为

(19)

多普勒中心相干性反映两个天线波束中心的指向一致程度，表示为

(20)

式中：Δfdc为多普勒中心差；Δfa为多普勒带宽。

配准相干性为

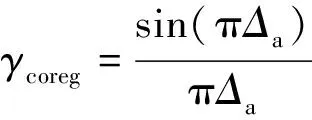
(21)

式中：Δa和Δr分别为方位向和距离向配准误差。

根据图3 相干系数与噪声标准差曲线，可以查找特定视数条件下γ对应的∂φdecor[7]。

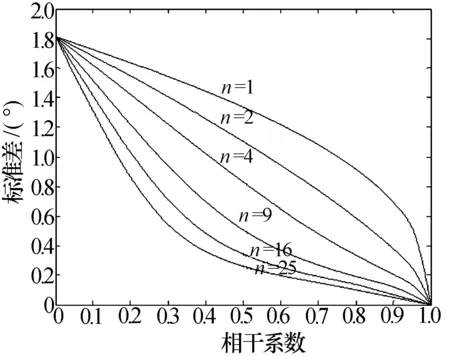
图3 多视条件下相干系数与相位噪声标准差的关系

4) 基线长度测量误差导致的测高误差

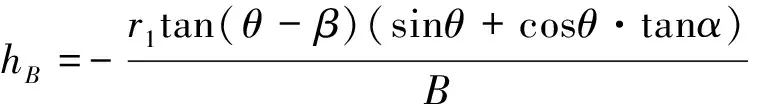
(22)

∂hB在刚性基线条件下，由基线长度测量误差引入，为一项系统误差，可通过外定标消除；而∂hB在非刚性基线条件下，由基线测量设备在机体测量坐标系中测量两个天线相位中心的位置误差和从机体测量坐标系转换到IMU惯性坐标系的转换误差引入[9]。

5) 基线倾角测量误差导致的测高误差

∂hβ=r1·(sinθ+cosθ·tanα)·∂β

(23)

∂hβ在刚性基线条件下，由惯导测量载机横滚角误差引入；而∂hβ在非刚性基线条件下，由基线测量设备在机体测量坐标系中测量两个天线相位中心的位置误差和从机体测量坐标系转换到IMU惯性坐标系的转换误差引入[9]。

3 InSAR系统设计和测高精度

从上一节对测高误差的分析可以看到InSAR系统设计要获得较高的高程精度，主要依赖减小干涉相位误差和在增长干涉基线的同时保证基线长度及倾角的测量精度。

本节来具体设计两部高、低频段InSAR系统，满足如下指标要求：(1)分辨率为1 m(方位)×1 m(距离)；(2)距离向幅宽为4 km；(3)测高精度约为1 m。

3.1 基线长度设计

考虑载机左右侧视要求，基线倾角通常设计在0°，即两副天线安装水平高度相同。基线长度的设计需要在小于临界基线的前提下寻找最优基线。

以“乒乓”模式为例，首先计算临界基线如下

B⊥C=Δfrr1λtan(θ-α)/c

(24)

其中，信号带宽Δfr取180 MHz以实现距离向1 m分辨率。对于X波段，波长λ为0.031 4 m，距离r1为8.5 km，下视角θ为45°，地形坡度角α为10°，则B⊥C等于111 m；对于P波段，波长λ为0.86 m，距离r1为8.5 km，下视角为45°，地形坡度角α为10°，则B⊥C等于3 055 m。显然，高低频段InSAR临界基线的差异由波长引入。而对于机载单航过的InSAR系统，基线长度受飞机机体限制，小于甚至远远小于上面计算的临界基线。

接下来，计算最优基线如下

(25)

γopt=0.618-1.171SNR-1

(26)

式中：γopt为相干系数；SNR为信噪比，取20 dB；ρr为距离分辨率。对于X波段，最优基线长度为51 m；对于P波段，最优基线长度为1 409 m。显然，这一最优基线在机载单航过干涉SAR系统中受机体结构尺寸的限制无法获得。

理论上，在基线长度未达到最优基线的情况下，基线越长，测高精度越高[4]，但在具体设计基线时，还需结合雷达频段、基线刚性及其测量精度综合考虑。测高精度受基线的影响的主要是式(14)、式(22)和式(23)。对于式(14)，在相位误差和成像几何关系一定的前提下，频段越低，波长越长，要求基线设计得越长。而对于式(22)和式(23)，在成像几何关系一定的前提下，基线长度和倾角与基线长度测量误差成正比：因为基线越长，基线的刚度越差，当超过一定的长度限制，基线就不再是一个刚体，需要引入基线测量设备进行精确测量，但即使用光学相机和激光测距器测量基线长度和倾角精度也仅为0.5 mm和0.005°[9],相对于刚性基线测量精度0.1 mm和0.000 3°[2]分别在5倍和16倍以上。

在距离r1为8.5 km，下视角为45°和地形坡度角α为10°的边界条件下，对比X波段和P波段，典型长度的刚性基线(2.4 m)和非刚性基线(20 m)配置下的式(14)、式(22)和式(23)测高误差见表1。

表1 X、P波段刚性/非刚性基线测高误差比较

从表1可以看到：为保证较高的测高精度，对于高波段InSAR，基线适宜设计较短，以保证足够的刚性要求,而如果基线设计到20 m,由于运动补偿相位误差加大和多普勒中心相干性减小会导致测高精度恶化；对于低频段InSAR，基线适宜设计得更长，甚至突破刚性要求。这样对于X波段InSAR系统，设计基线为长度2.4 m的刚性结构；对于P波段InSAR系统，利用机翼的展向长度，设计基线为长度20 m的非刚性结构。

3.2 测高误差源分析

斜距测量误差与频段无关，主要由系统延迟和定时抖动决定，通过外定标可以消除绝大部分误差分量，一般取20 cm左右[10]。

平台高度误差主要由GPS高度测量误差引入，一般地面差分处理可以达到3 cm测量精度[2]。

相位误差主要由运动补偿相位误差和干涉相干性决定。对于刚性基线，由于两个天线相位中心的扰动相同，两幅SAR图像的相位有较强的相干性，可以在干涉处理过程中绝大部分抵消；而非刚性基线，由于两个天线相位中心的扰动不同，干涉处理会保留较大部分相位误差。这里对场景中不同位置不同高度的9个点目标进行回波仿真，然后经运动补偿成像和干涉处理，最后计算其干涉相位与理论干涉相位的差值，如图4所示。

图4 成像运动补偿引入的干涉相位误差

从图4中可以看到：前者相位误差在10-4量级，几乎可以忽略；而后者相位误差在1°左右(而如果是X波段，根据波长的等比例关系，干涉相位误差要超过27°)。

干涉相干性主要与目标信噪比、干涉成像空间关系、地表体散射、多普勒中心重合度和配准精度有关。

图5绘制了热噪声相干性与目标信噪比的关系曲线。

图5 热噪声相干性随信噪比的变化

从图5可以看到：信噪比大于等于20dB，热噪声相干性在0.99以上；经25视以上处理后，相位误差可小于1°。因此，设计InSAR系统要求SAR成像信噪比应大于等于20dB。

图6绘制了空间相干性与入射角的关系曲线。

图6 空间相干性随入射角的变化

图6中，在10°地形坡度角和入射角45°条件下，X波段空间相干性大于0.99，P波段大于0.997。虽然P波段基线20m大于X波段2.4m，但因为P波段临界基线大，所以空间相干性大。

图7绘制了体散射相干性与入射角的关系曲线。

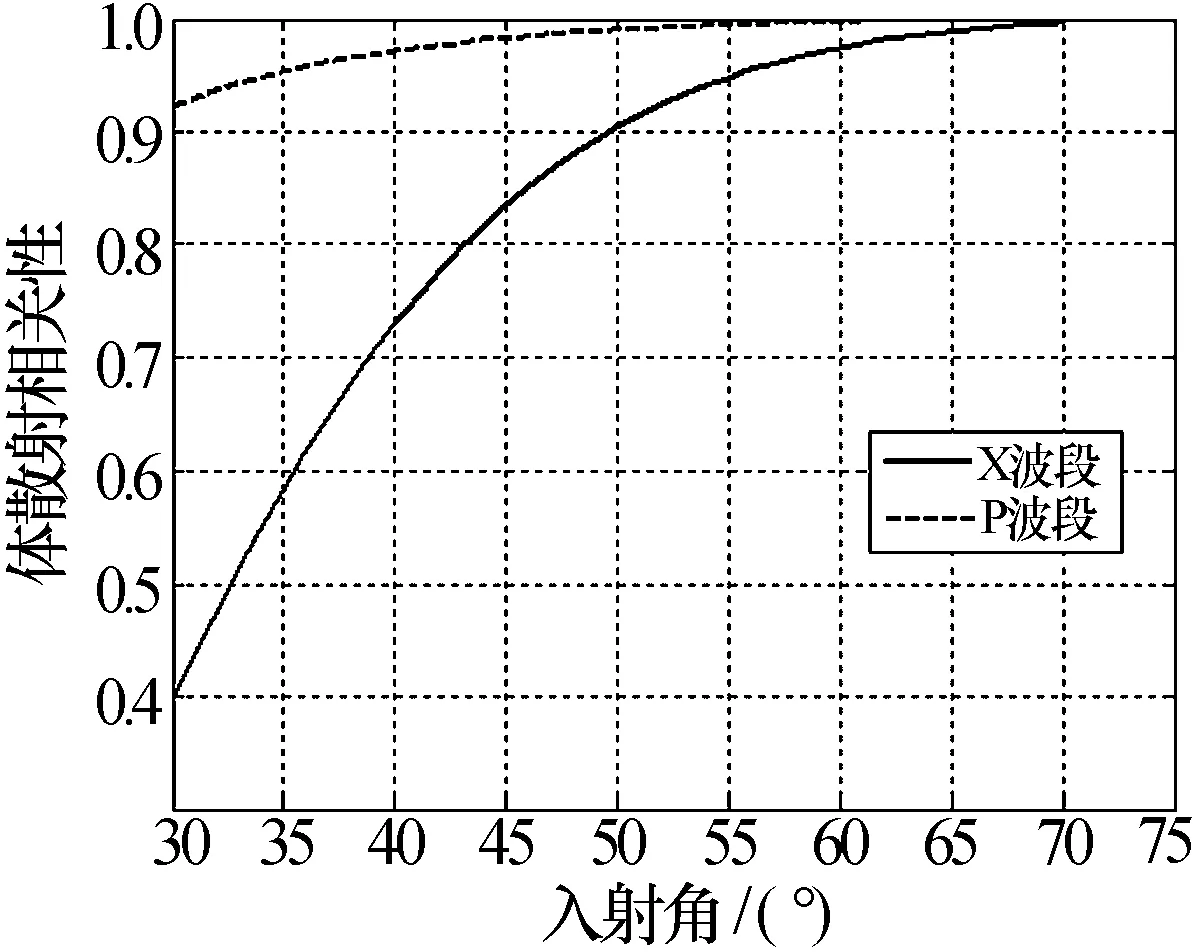
图7 体散射相干性随入射角的变化

从图7中可以看到：45°入射角条件下，X波段和P波段体散射相干性分别为0.840和0.984，低波段体散射相干性较大；高波段体散射相干性较小。

多普勒中心相干性，在刚性基线条件下，X波段两副天线波束指向近似一致，可取0.99；在非刚性基线条件下，由于P波段两副天线受到的扰动不同，如果天线波束指向偏差为1°～2°，且考虑方位1.5m长P波段天线方位波束在20°～40°。因此，多普勒中心相干性可取0.95；若方位1.5m长X波段天线方位波束宽度本身为1°～2°，多普勒中心相干性则小于0.1。

图8绘制了配准相干性与配准精度的关系曲线。

图8 配准相干性随配准精度的变化

从上图可以看到：配准精度优于1/20个像素，配准相干性大于0.99。因此，InSAR处理两幅SAR图像配准精度应小于等于1/20像素。

在单航过条件下，时间相干性等于1。

基线长度测量精度，在刚性基线条件下可以达到0.1mm；用经纬仪在地面静态测量，同时测量载机飞行状态下的温度变化进行补偿，另外，通过外定标也可校正该系统误差[2]。在非刚性基线条件下，基线长度测量精度可以达到0.5mm；主要通过激光和相机组合测量两个天线相位中心的三维坐标进行计算[9]。

基线倾角测量精度，在刚性基线条件下主要由IMU的横滚角测量精度引入，可以达到0.003°，进一步通过外定标，还可提高到0.000 3°[2]。在非刚性基线条件下，基线倾角测量精度可以达到0.005°[9]；主要通过激光和相机组合测量两个天线相位中心的三维坐标进行计算[9]。

综上，汇总X波段和P波段InSAR误差源参数见表2。

表2 测高误差源误差分配

3.3SAR系统设计与图像信噪比

SAR系统设计主要确定雷达功率、孔径和信号带宽等参数。为保证条带SAR成像1m(方位)×1m(距离)的空间分辨率，即

(27)

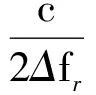
(28)

这里两维加权展宽因子取1.2，天线方位向长度La取1.5 m，Δfr取180 MHz。

为了保证45°视角下，距离向覆盖大于等于4 km，对于X波段，天线距离向长度 为0.035 m；对于P波段，天线距离向长度 为0.381 m。

在载机功耗一定的条件下，对于X波段和P波段，平均辐射功率Pav均取100 W。

在地形坡度角α=10°的情况下， 计算成像SNR如下

(29)

其中，脉冲宽度τ均取40 μs；波长λ取0.031 m和0.86 m；视数M均取1；r为斜距；载机速度Vp为200 m/s；重复频率PRF均取1 kHz；天线增益Gt≈Gr，取27.6 dB和9.3 dB；波尔兹曼常数k=1.38×10-23；T0=290 K；噪声系数Fn分别取4 dB和3 dB；接收机带宽Bn≈Δfr；系统损耗Ls分别取5 dB和3.5 dB；归一化平均后向散射系数γ=-10 dB。

根据式(29)计算X、P波段雷达单视SAR图像的信噪比分别如图9所示。

图9 单视SAR图像信噪比随斜距的变化

从图中可以看到，在斜距6.5 km～10.5 km的范围内，X波段成像信噪比在33 dB以上，P波段成像信噪比在43 dB以上，均大于信噪比20 dB的要求。

3.4 测高灵敏度

干涉相位的高度灵敏度定义为

(30)

即引起一个2π相位变化所对应的高度变化。在频段、斜距和入射角一定的条件下，有效基线B⊥越小，高度灵敏度越小，干涉条纹越稀疏，相位展开越容易，但一般测高精度越低。

根据式(30)计算平台高度为6 000 m、中心视角为45°和“乒乓”模式情况下测高灵敏度随斜距的变化，如图10所示。

图10 高度灵敏度随斜距的变化

从图10可以看到X、P频段波长相差超过一个数量级，基线相差接近一个数量级，因此X、P频段干涉测量的高度灵敏度基本上在同一数量级。

因此，同时设计X、P波段InSAR系统时，为保证干涉条纹的疏密近似相同，P频段InSAR系统需要拉长基线，以抵消其波长较长测高灵敏度低的影响。

3.5 高程测量精度

对于X波段InSAR系统，在刚性基线条件下基线长度可以看作不变，基线误差可以认为是一项系统误差，因此高程误差主要由测距误差、高度误差、相位误差和基线倾角测量误差引入，可以表示为

(31)

对于P波段InSAR系统，在非刚性基线条件下，高程误差由全部5项误差源引入，即测距误差、高度误差、相位误差、基线倾角测量误差和基线长度测量误差，可以表示为

(32)

因此，分别计算X、P波段InSAR高程测量精度如图11所示。其中，地形坡度角取10°；视数取25，对应地图比例尺为1∶5000。

从图11中可以看到，在场景中心8.5 km处，X波段InSAR系统高程精度可达0.82 m，而P波段InSAR系统高程精度可达1.33 m，近距段可以达到0.5 m。因此，X波段和P波段InSAR测高精度可以满足1 m的要求。

图11 高程测量精度随斜距的变化

4 结束语

对于高、低波段的InSAR系统，在空间相干性、体散射相干性和基线参数测量精度等因素的影响下，需要分别采用刚性基线和非刚性基线方案来实现InSAR较高的测高精度。对于高波段的InSAR系统，刚性基线长度可设计在2 m左右，这样由相位误差所引入的高程误差并不大，且基线参数测量精度高；由于基线长度几乎恒定不变化，可作为系统误差不引入到测高误差中；刚性基线上的两个天线相位中心的扰动相同，成像运动补偿后引入的相位误差可以相互抵消。对于低波段InSAR系统，基线可以设计到20 m左右，以抵消其波长造成高程误差(由相位误差引入)大的影响，但载机需要加装高精度的基线测量设备进行实时测量，而基线长度测量误差会引入到高程测量中去。

[1] Okada Y, Hirao C. Highly accurate DSM reconstruction using Ku-band airborne InSAR[C]// IEEE International Geoscience and Remote Sensing Symposium.Barcelona, Spain：IEEE Press, 2007: 5049-5052.

[2] Wimmer C, Siegmund R, Schwäbisch M, et al. Generation of high precision DEMs of the wadden sea with airborne interferometric SAR[J]. IEEE Transactions on Geosci Remote Sensing, 2000, 38(5): 2234-2245.

[3] Wheeler K, Hensley S. The GeoSAR airborne mapping system[C]//IEEE International Radar Conference. Alexahdria, VA: IEEE Press, 2000: 831-835.

[4]RodriguezE,MartinJM.Theoryanddesignofinterferometricsyntheticapertureradars[J].RadarandSignalProcessing,IEEProceedingsF, 1992, 139(2): 147-159.

[5] 保 铮，邢孟道，王 彤. 雷达成像技术[M]. 北京：电子工业出版社，2005.BaoZheng,XingMengdao,WangTong.Radarimagingtechnology[M].Beijing：PublishingHouseofElectronicsIndustry, 2005.

[6]YounisM,MetzigR,KriegerG,etal.PerformancepredictionandverificationforthesynchronizationlinkoftanDEM-X[J].IEEEGeoscienceRemoteSensingLetters, 2007, 6(3): 5206-5209.

[7]LeeJS,HoppelKW,MangoSA.IntensityandphasestatisticsofmultilookpolarimetricandinterferometricSARimagery[J].IEEETransactionsonGeoscienceRemoteSensing, 1994, 32(5): 1017-1027.

[8]RosenPA,HensleyS,JoughinIR.Syntheticapertureradarinterferometry[J].ProceedingsoftheIEEE, 2000, 88(3): 333-382.

[9]KimYJ,HensleyS,VeilleuxL,etal.DesignconsiderationsofGeoSAR[C] //RadarSensorTechnology.Orlando,Florida:NorthropGrummanCorp, 1996: 27-47.

[10]MallorquíJJ,RosadoI,BaraM.InterferometriccalibrationforDEMenhancingandsystemcharacterizationinsinglepassSARinterferometry[C]//IEEEInternationalGeoscienceandRemoteSensingSymposium.Sydney,Australia:IEEEPress, 2001: 404-406.

武 楠 男，1979年生，高级工程师。研究方向为机载成像雷达系统设计、天基雷达系统设计。

System Design of An Airborne High and Low Band InSAR with Two Distributed Antennas

WU Nan，HE Dongyuan，HU Xuecheng，LIN Youquan

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

The theory of measuring terrain height by an airborne interferometric synthetic aperture radar (InSAR) is introduced, the model of an airborne InSAR system is built, and the equations of signal receiving and processing are developed. Then all the error sources of measuring terrain height by an airborne InSAR are deeply analyzed. A comparison is made between the high band InSAR with the rigid baseline structure and the low band InSAR with the non-rigid baseline structure. In terms of the resolution and height accuracy required, the form and length of baselines are optimally selected and the effect of error sources is analyzed on the accuracy of digital elevation model (DEM). Finally，the Signal Noise Ratio (SNR) of SAR imaging, the sensitivity and accuracy of measuring terrain height are computed, which conclusions can be regarded as a good reference in the design of an airborne InSAR system.

airborne radar; InSAR; baseline; system design; DEM

10.16592/ j.cnki.1004-7859.2015.09.002

武楠 Email：xidianwunan@163.com

2015-04-30

2015-07-22

TN

A

1004-7859(2015)09-0005-08