基于EMD－BPN方法的高速铁路短期客流预测

曹 承，梁院生

（兰州交通大学 交通运输学院，甘肃 兰州730070）

短期客流预测是交通系统的重要组成部分，稳定以及精确的客流预测能够为旅客出行提供更加便利的条件和服务。短期客流预测的方法根据自变量和因变量是否具有函数依赖关系，一般分为两类:参数方法和非参数方法。参数方法主要包括:历史平均法，指数平滑法和差分自回归移动平均模型（ARIMA）等。其中ARIMA方法及其改进方法对于线性和静态的时间序列有着较为精确的预测能力，从20世纪80年代开始被广泛应用于交通流、旅行时间、客流量的预测中。但是ARIMA方法及其改进方法要求时滞变量具有线性关系，因此，对于预测序列中的非线性关系的处理能力不尽如人意。最近，Huang等介绍了一种分析非线性非静态数据的希尔伯特－黄变换（HHT）方法。由于EMD方法能够将原始数据分解成很多小的独立的部分，一些学者研究了混合EMD方法，通过EMD方法和预测模型相结合来获得更好的结果。Hamad等提出了一种基于EMD方法和BP神经网络的混合方法来预测短期交通速度。冯平等提出基于EMD的降雨径流神经网络预测模型。Yu Wei等用EMD方法和BP神经网络的混合方法来预测地铁客流量。截至目前，关于高速铁路客流短期预测的文献仍然较少。通过结合高铁短期客流特征，提出了EMD方法和神经网络方法的高速铁路短期客流预测模型，通过将EMD分解得到的各IMF分量按照一定的数学方法组合，设计4种混合模型分析。

1 模 型

1.1 EMD

经验模态分解（EMD）方法是一种全新的处理非平稳数据序列的方法，EMD方法将时间信号X（t）分解成一系列本征模态函数IMF。

1.2 BP神经网络

BP神经网络也称误差反向传播神经网络，是一种有监督的学习，是梯度下降法在多层前馈网络中的应用。BP算法的学习过程是一个反复迭代的过程，由正向传播和反向传播组成。其算法的基本思想是根据网络输出层的误差，从输出层开始反过来调整网络的权值和阀值，最后使得输出的均方误差最小。

1.3 EMD-BPN混合预测模型

这里提出一种结合经验模态分解和BP神经网络的混合方法来预测高速铁路短期客流。混合模型主要分为三个阶段:EMD分解，EMD分量识别，神经网络预测，如图1所示。

图1 EMD-BPN混合预测模型

1.3.1 EMD阶段

将原始客流时间序列分解成为很多IMFs分量，分离出的IMFs分量表示频率从高到低的变化范围，以及客流的不同周期模式。每个IMFs分量代表时间序列的局部特点。

1.3.2 分量识别阶段

识别有意义的IMFs分量。分离出的IMFs分量频率从高到低，高频代表短期模式，低频代表长期模式。为了构建合适的短期客流预测模型，有必要识别出有意义的IMFs分量。

1.3.3 神经网络阶段

为了验证不同预测模式的表现，文中采取了独特的方式分离IMFs分量。首先，反映原始数据的独立模式的IMF分量作为输入；其次，考虑输入变量和计算维度，分离的IMFs分量以单独或者合并的方式作为输入；最后，高相关性的IMFs分量单独或者合并的方式作为输入，低相关性的IMFs分量合并作为输入。

1.4 预测模型设计

将数据划分为训练集和测试集。以2010－01－01～2011－05－30客流为训练集，2011－05－31～2011－10－30为测试集。训练数据用来得到权重和偏差，试验数据用来验证预测模型的有效性。在输入BP神经网络之前，对数据进行归一化。

输入层的输入元素包括客流数据、客流模式和时空因素。客流模式包括有意义的分量和其他分量。有意义的分量作为单独输入或者合并输入，因为跟原始数据强相关。其它分量考虑计算的维度来单独输入或者合并输入。输入节点的数量根据周期确定，铁路客流一般以一周为周期。根据使用不同的IMF输入，设计四种混合EMDBPN模型。

2 实例分析

2.1 数据

选取2010－01－01～2011－10－30期间，武广高速铁路武汉－广州区间669天的日客流数据作为算例。

2.2 IMF分量分离

在EMD阶段，运用模态分解技术对客流进行模态划分，通过 MATLAB导入EMD包，编程得到。

2.3 IMF分量识别

分量识别阶段，同样采用MATLAB编程，将分离得到的IMF各个分量分别与原始序列进行皮尔逊相关分析，如表1所示。

表1 皮尔逊相关系数

3 结果和分析

文中数据采用IBM酷睿双核，内存2G，主频1.7GHz计算机辅助计算。设计四种混合模型，如表2所示。

表2 混合EMD-BPN模型的输入变量和输入变量个数

表3总结了通过四种混合EMD－BPN模型得到的MAPE结果值。其中EMD－BPN3和EMDBPN4的平均MAPE值较小。结果表明，将高相关性分量和低相关性分量分开作为输入变量能够得到更好的预测结果。

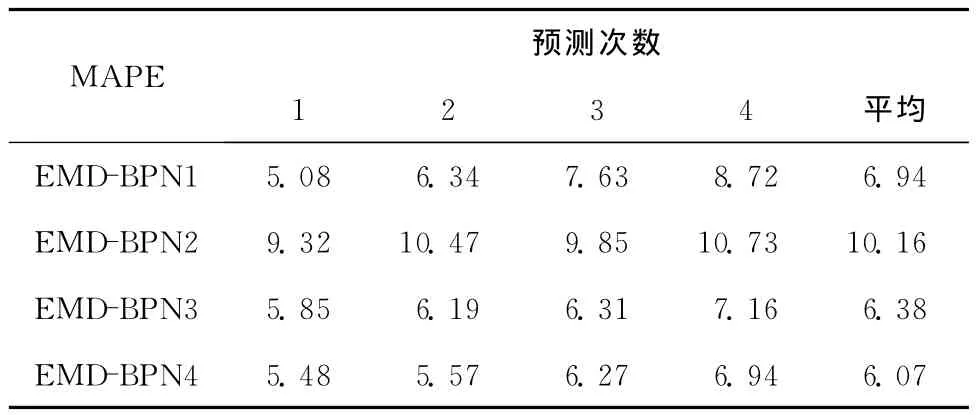
表3 混合EMD-BPN模型4次测试数据MAPE值%

4 结束语

高速铁路客流预测，无论是对于开行方案的制定，还是对于营销部门采取正确的营销策略和制定良好的客流组织疏导方法，都具有重大的现实意义。文中提出了三个阶段的EMD－BPN混合预测模型，将有强相关性的IMF分量与弱相关性的IMF分量分开，作为输入能够得到更为准确的预测结果。但EMD方法也存在不足之处，通过EMD分解得到的IMF分量往往分解的不够充分，存在模式混叠现象，进一步的研究可采用EEMD方法，来代替EMD方法。

［1］ Smith，B.L.，Williams，B.M.，Keith Oswald，R.，.Comparison of parametric and nonparametric models for traffic flow forecasting［J］.Transportation Research Part C，2002，10 （4）:303－321.

［2］ Vlahogianni，E.I.，Golia，J.C.，Karlaftis，M.G.，.Short－term traffic forecasting:overview of objectives and methods［J］.Transport Reviews，2004，24 （5）:533－557.

［3］ Huang，N.E.，Shen，Z.，Long，S.R.，Wu，M.C.，Shih，H.H.，Zheng，Q.，Yen，N.－C.，Tung，C.C.，Liu，H.H.，.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proceedings of the Royal Society，1998，454（1971）:903－995.

［4］ Hamad，K.，Shourijeh，M.T.，Lee，E.，Faghri，A.，.Near－term travel speed prediction utilizing Hilbert－Huang transform.Computer－Aided Civiland Infrastructure Engineering，2009，24（8）:551－576.

［5］ 冯平，丁志宏，韩瑞光，等.基于EMD的降雨径流神经网络预测模型［J］.系统工程理论与实践，2009，29（1）:1000－6788.

［6］ Yu Wei，Mu－Chen Chen.Forecasting the short－term metro passenger flow with empirical mode decomposition and neural networks［J］.Transportation Research Part C，2011，21（2012）:148－162.

［5］ 曾玮，王佟.基于列车时刻表的城际铁路客流分配研究［J］.交通科技与经济，2014，16（2）:24－26.