基于层次分析法和模糊评价法的电动汽车充电站选址研究

姚 龙

(华北电力大学 经济管理学院，河北 保定 071000)

基于层次分析法和模糊评价法的电动汽车充电站选址研究

姚 龙

(华北电力大学 经济管理学院，河北 保定 071000)

针对当今电动汽车充电站选址采用的方法存在考虑因素的不完整性，笔者提出将层次分析法和模糊评价法两种方法结合起来，构建评价指标体系以及模糊层次评价模型，然后对拟定的两个备选电动汽车充电站地址进行综合评价，实现最优选址。实践证明，该方法具有高度的精确性。

电动汽车；充电站；层次分析法；模糊评价法；评价指标体系

近年来，中国的能源危机在不断加深，而且环境污染严重，如重金属冶炼、化工和煤矿企业等废气排放造成的雾霾天气，给人类带来了极大伤害。面对这样日益紧张的环境和资源的双重压力下，电动汽车作为新能源汽车的典型代表，因其具有零排放、低能耗的特点而被广大汽车行业及各界人士看好。

虽然电动汽车行业在中国还处于起步阶段，但是中国汽车行业研发人员以及各界学者已经对电动汽车充电站选址进行了一定程度的理论研究。文献[1]建立了一种考虑多因素的电动汽车充电站选址定容模型，采用自适应粒子群算法进行求解，并通过一个算例验证了该模型的可行性。文献[2]建立了一种电动汽车充电站选址定容的最优费用模型，采用粒子群算法对一假设算例进行优化求解，结果表明该模型具有一定的可行性。该模型的缺陷在于用层次分析法确定权重的精度不高。文献[3]建立了基于用户分类的电动汽车充电站需求预测模型，为区域电动汽车充电站需求预测提供了一定的理论参考。文献[4]充分考虑了电动公交汽车换电电量需求和充换电行为，提出了一种换电站电池充电站建设模式，并给出了相应的优化规划方法。文献[5]在进行选址时，主要考虑充电需求、交通条件、服务区域覆盖、建设等条件在内的交通与使用约束条件，其缺陷在于没有将影响因素考虑全面。文献[6-8]在考虑了城市交通网络布局、地段的适应性以及地价成本等地理因素以及服务半价的基础上，确定了候选地址。但是大多只涉及到了片面选址因素，很少有文献能将影响电动汽车充电站选址方面的多种因素包含进去，并且大多数研究文献只用到了一种方法，因此存在一定的弊端。基于这种情况，本文在综合考虑了成本费用、未来规划、电网现状及地理情况等几大方面因素的基础上，提出了层次分析法和模糊评价法相结合的综合评价方法。

1 层次分析法

1) 构造判断矩阵。将本层次的评价要素相对于上一层次要素按重要程度进行两两比较，得到的矩阵如表1所示，其比较的标准是按照9级标度[9]，如表2所示。

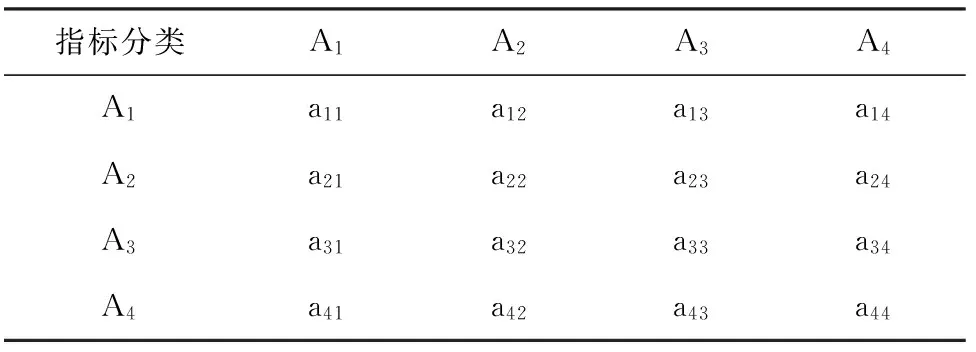
表1 判断矩阵

表2 9级标度值

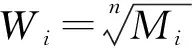
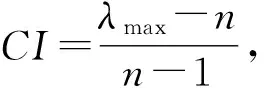
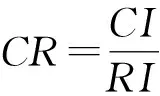
表3 RI取值表

若满足CR≤0.1，则判断矩阵构造成立；反之，则需重新构造判断矩阵。

2 模糊评价法

1) 确定影响评价结果的主要因素：

用X来表示评价因素集合，即X=(X1,X2,…,Xm)。

2) 确定描述评价结果的评语：

用Y来表示评语集合，即Y=(Y1,Y2,…,Yn)。

3) 单因素评价：

对单个因素进行评价，对每一个因素的评价结果都是Y上的模糊集合。评价结果为矩阵R。

i=1，2，…，m；j=1，2，…，n

其中，rij表示第i个因素隶属于第j个评语的程度。

4) 确定权重：

各因素的权重用A来表示，即A=(A1,A2,…,Am)。

5) 进行综合评价：

B表示评价结果矩阵，有B=AR，通过计算得出B=(B1,B2,…,Bn)。

3 具体算例分析

3.1 层次分析法确定各指标权重

在某个区域建一座充电站，考虑的因素应有如下几方面：

1) 成本费用因素。成本费用主要包括投资、运行和维护成本，以及其他费用如网损费用，辅道建设费用，人员工资和配电变压器的投资费用等。

2) 规划因素。规划因素主要包括交通网络规划，配电系统的现状与远期规划，电动汽车发展规划等。

3) 电网因素。电网因素主要包括电网承受能力、负荷平衡[13]、电能质量、供电可靠性[14]等因素。

4) 地理因素。地理因素包括人群密集度、道路路况、交通流量 、公共设施等因素。

根据以上信息，作出评价体系指标图，如图1所示。

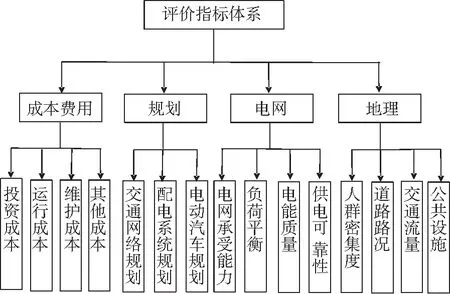
图1 评价指标体系图

根据9级标度，得到的判断矩阵如表4～8所示。

表4 成本费用、规划、电网、地理等因素的判断矩阵

Tab.4 Judgment matrix including cost, planning,power grid, geographical factors

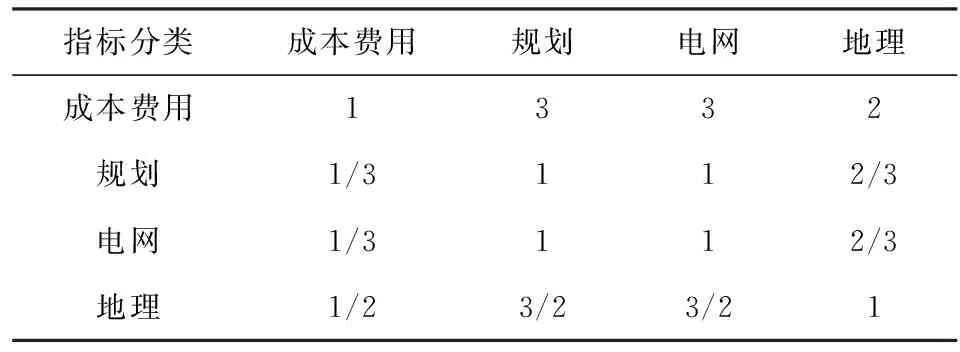
指标分类成本费用规划电网地理成本费用1332规划1/3112/3电网1/3112/3地理1/23/23/21

计算得出：M0=(18,0.222,0.222,1.125)，W0=(2.060,0.686,0.686,1.030)。

归一化得到成本费用、规划、电网、地理等因素的相对权重分别为K0=(0.461,0.154,0.154,0.231)，λmax为4.002，CI为0.0007，RI为0.89，CR为0.0008<0.1。故通过一致性检验。

表5 成本费用指标下的各指标判断矩阵

Tab.5 Judgment matrix of the indexes under cost index

指标分类投资成本运行成本维护成本其他成本投资成本1466运行成本1/413/23/2维护成本1/62/311其他成本1/62/311

计算得出：M1=(18,0.563,0.111,0.111)，W1=(2.060,0.866,0.577,0.577)。

归一化得到投资成本、运行成本、维护成本、其他成本等因素的相对权重分别为K1=(0.632,0.158,0.105,0.105)，λmax为4.002，CI为0.0007，RI为0.89，CR为0.0008<0.1。故通过一致性检验。

表6 规划指标下的各指标判断矩阵

Tab.6 Judgment matrix of the indexes under planning index

指标分类交通网络规划配电系统规划电动汽车规划交通网络规划121/2配电系统规划1/211/4电动汽车规划241

计算得出：M2=(1,0.125,8)，W2=(1,0.595,1.682)。

归一化得到交通网络规划、配电系统规划、电动汽车规划等因素的相对权重分别为K2=(0.286,0.143,0.571)，λmax为3.001，CI为0.0005，RI为0.5，CR为0.00025<0.1。故通过一致性检验。

表7 电网指标下的各指标判断矩阵

Tab.7 Judgment matrix of the indexes under power grid index

指标分类电网承受能力负荷平衡电能质量供电可靠性电网承受能力1134负荷平衡1134电能质量1/31/314/3供电可靠性1/41/43/41

计算得出：M3=(12,12,0.148,0.047)，W3=(1.861,1.861,0.620,0.465)。

归一化得到电网承受能力、负荷平衡、电能质量、供电可靠性等因素的相对权重分别为K3=(0.387,0.387,0.129,0.097)，λmax为4.001，CI为0.0003，RI为0.89，CR为0.0003<0.1。故通过一致性检验。

表8 地理指标下的各指标判断矩阵

Tab.8 Judgment matrix of the indexes under Geography index

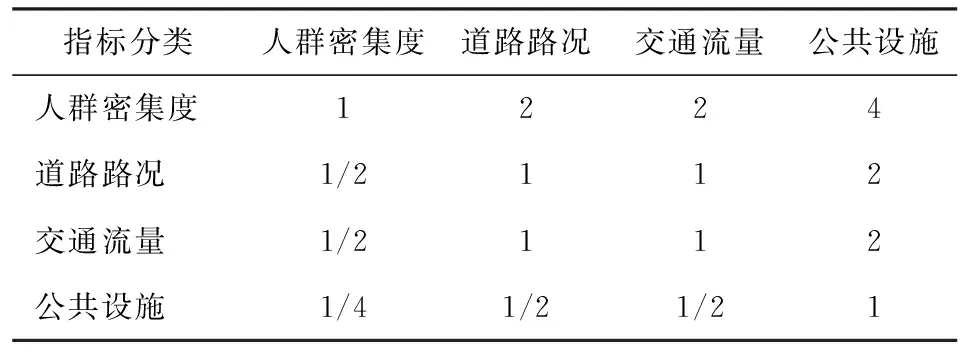
指标分类人群密集度道路路况交通流量公共设施人群密集度1224道路路况1/2112交通流量1/2112公共设施1/41/21/21

计算得出：M4=(16,1,1,0.063)，W4=(2,1,1,0.5)。

归一化得到人群密集度、道路路况、交通流量、公共设施等因素的相对权重分别为K4=(0.444,0.222,0.222,0.111)，λmax为4，CI为0，RI为0.89，CR为0<0.1。故通过一致性检验。

3.2 模糊评价法进行综合评价

3.2.1 一级评价

目前，在考虑这些评价指标后，共有两处备选地址符合条件，分别为甲地址和乙地址。共有10名专家对这些评价指标按“很好”、“较好”、“一般”、“较差”四个等级来评价，结果如表9所示。

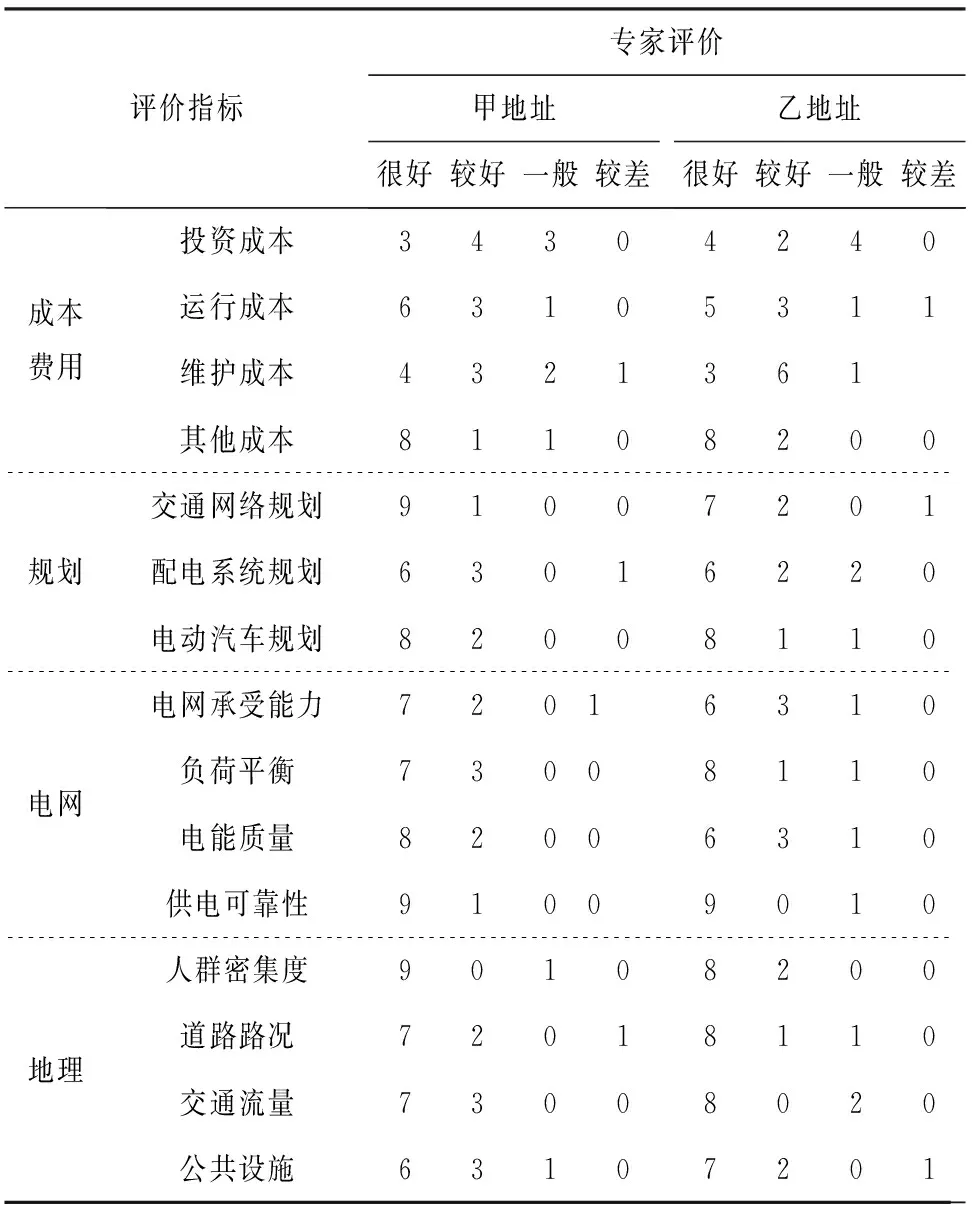
表9 专家评价结果表

根据表9可知，甲、乙备选地址的模糊评价矩阵有

则根据综合评价公式得

B1甲=K1C1甲=(0.410,0.342,0.237,0.110)

B1乙=K1C1乙=(0.447,0.258,0.279,0.016)

B2甲=K2C2甲=(0.800,0.186,0.000,0.014)

B2乙=K2C2乙=(0.743,0.143,0.086,0.029)

B3甲=K3C3甲=(0.732,0.229,0.000,0.039)

B3乙=K3C3乙=(0.707,0.194,0.100,0.000)

B4甲=K4C4甲=(0.777,0.144,0.056,0.022)

B4乙=K4C4乙=(0.788,0.133,0.067,0.011)

由此可知，从成本费用因素来考虑，甲地址隶属于较好及以上的隶属度为0.752，而乙是0.705，说明从成本费用这方面考虑，甲地址优于乙地址；从规划因素来考虑，甲地址隶属于较好及以上的隶属度为0.986，而乙是0.886，说明从规划这方面考虑，甲地址优于乙地址；从电网因素来考虑，甲地址隶属于较好及以上的隶属度为0.961，而乙是0.901，说明从电网这方面考虑，甲地址优于乙地址；从地理因素来考虑，甲地址隶属于较好及以上的隶属度为0.921，而乙是0.921，说明从地理这方面考虑，甲、乙两地址旗鼓相当。

3.2.2 二级评价

由以上可知，甲乙地址总的模糊评价矩阵为

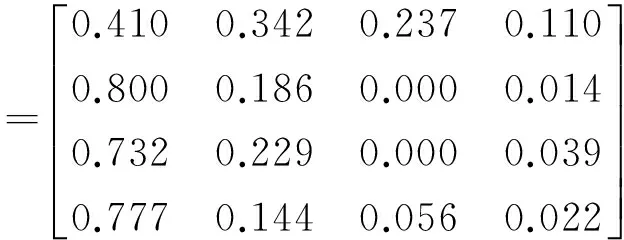
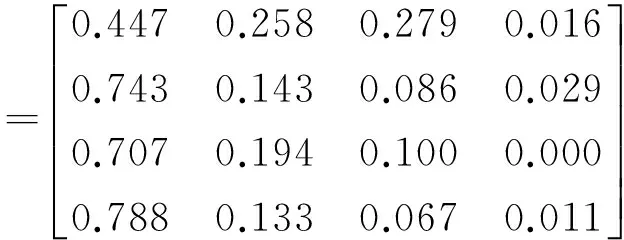
则根据公式A=K0B得：

A甲=K0B甲=(0.604,0.255,0.122,0.079)

A乙=K0B乙=(0.611,0.202,0.173,0.014)

按专家组给出的评价对这些评语赋予权重，令“很好”为100，“较好”为80，“一般”为60，“较差”为40，即得到了两备选地址的总分：

甲地址总分为100×0.604+80×0.255+60×0.122+40×0.079=91.28

乙地址总分为100×0.611+80×0.202+60×0.173+40×0.014=88.20

很明显甲地址要优于乙地址，应选择甲地址。

4 结 论

本文在综合考虑了成本费用、未来规划、电网现状及地理情况等几大方面因素的基础上，提出了层次分析法和模糊评价法相结合的综合评价方法。首先通过用层次分析法来确定评价体系中各指标的权重，使各指标的权重更加精确，排除了主观因素的干扰，从而使得指标权重更加客观。然后通过模糊评价法进行定量分析、综合评定。实际算例表明，该方法比单独利用层次分析法或者模糊评价法的精确度都要高，因此具有高度的有效性、可行性。

[1] 谢林伟．基于自适应粒子群算法的电动汽车充电站优化规划[J]．陕西电力，2012(11)：34-37. XIE Linwei. Adaptive PSO algorithm based optimal planning of charging station for electric vehicle [J]. Shanxi Electric Power, 2012(11)：34-37.

[2] 寇凌峰，刘自发，周欢．区域电动汽车充电站规划的模型与算法[J]．现代电力，2010，27(4)：44-48. KOU Lingfeng, LIU Zifang, ZHOU Huan. Modeling algorithm of charging station planning for regional electric vehicle [J]. Modern Electric Power, 2010，27(4)：44-48.

[3] 王飞龙，孙凯航，李燕青．基于用户分类的电动汽车充电站需求预测[J]．黑龙江电力，2013，35(02)：132-134. WANG Feilong, SUN Kaihang, LI Yanqing. Demand forecast of electric vehicle charging stations based on customer classification [J]. Heilongjiang Electric Power, 2013，35(02)：132-134.

[4] 钱斌，石东源，谢平平，等．电动公交车换电站-电池充电站优化规划[J]．电力系统自动化，2014，38(2)：64-69. QIAN Bin, SHI Dongyuan, XIE Pingping, et al. Optimal planning of battery charging and exchange stations for electric vehicl-es [J]. Automation of Electric Power Systems, 2014，38(2)：64-69.

[5] 郭春林，肖湘林．电动汽车充电基础设施规划方法与模型[J]．电力系统自动化，2013，37(13)：70-75. GUO Chunlin, XIAO Xianglin. Planning method and model of electric vehicle charging infrastructure [J]. Automation of Electric Power Systems, 2013，37(13)：70-75.

[6] 刘志鹏，文福栓，薛禹胜，等．电动汽车充电站的最优选址和定容[J]．电力系统自动化，2012，36(3)：54-59. LIU Zhipeng, WEN Fushuan, XUE Yusheng, et al. Optimal siting and sizing of electric vehicle charging stations [J]. Automation of Electric Power Systems, 2012，36(3)：54-59.

[7] 唐现刚，刘俊勇，刘友波，等．给予计算几何方法的电动汽车充电站规划[J]．电力系统自动化，2012，36(8)：24-30. TANG Xiangang, LIU Junyong, LIU Youbo, et al. Electric vehicle charging station planning based on computational geometry meth-od [J]. Automation of Electric Power Systems, 2012，36(8)：24-30.

[8] 刘自发，张伟，王泽黎．基于量子粒子群优化算法的城市电动汽车充电站优化布局[J]．中国电机工程学报，2012，32(22)：39-45. LIU Zifa, ZHANG Wei, WANG Zeli. Optimal planning of charging station for electric vehicle based on quantum PSO algorithm [J]. Proceedings of the CSEE, 2012，32(22)：39-45.

[9] 张涛．基于层次分析法的物流中心选址研究[D]．武汉：武汉科技大学，2008 ZHANG Tao. Research on the siting for logistic center based on analytic hierarchy process [D]. Wuhan: Wuhan University of Science and Technology, 2008.

[10] 廖培．AHP与模糊评价法相结合的旅游投标方案评价[J]．求索，2010(02)：15-17 LIAO Pei. Evaluation on tourism bidding scheme based on the combination of AHP and fuzzy method [J]. Seeker, 2010(02)：15-17.

[11] MEHAR,S,SENOUCI,S.M.An optimization location scheme for electric charging stations[J].Smart Communications in Network Technologies(SaCoNeT),2013International Conference on, 2013:1-5.

[12] PRAVIN KUMAR，RAJESH K.SINGH．A fuzzy AHP and TOPSIS methodology to evaluate 3PL in a supply chain[J]．Journal of Modelling in Management，2012，Vol.7(3)：287-303.

[13] 杨铎，王淼，乔琪．基于行驶状况的电动汽车充电负荷交通预测法[J]．黑龙江电力，2014，36(6)：539-546. YANG Duo, WANG Miao, QI Qi. Prediction method for electric vehicle charging load based on driving conditions [J]. Heilongjiang Electric Power, 2014，36(6)：539-546.

[14] 徐明宇，穆兴华，张惠，等．电动汽车充电站对电网谐波影响分析[J]．黑龙江电力，2012，34(1)：41-43. XU Mingyu, MU Xinghua, ZHANG Hui, et al, CHEN Xiaoguang. Analysis of the influence of the electrical vehicle charging station to the grid harmonic wave [J]. Heilongjiang Electric Power, 2012，34(1)：41-43.

(责任编辑 郭金光)

Research on site selection for electric vehicle charging stations based on AHP and fuzzy evaluation method

YAO Long

(School of Economic and Management Administration, North China Electric Power University, Baoding 071000, China)

Aiming at the defects of the existing site selection for electric vehicle charging station, such as the incomplete consideration, the author proposes to combine the two methods, AHP and fuzzy evaluation, to establish the evaluation index system and fuzzy hierarchy evaluation model, so as to make the optimal site selection through the comprehensive evaluation on the two alternative site for electric vehicle charging station. The practice proves that the method proposed enjoys high accuracy.

electric vehicles; charging station; AHP; fuzzy evaluation method; evaluation index system

2015-01-17。

国家自然科学基金项目(71201057)。

姚 龙(1994—),男，在读硕士研究生。

U469.72

A

2095-6843(2015)04-0313-05