驻波能量及能流密度局部振荡理论探析
李爱芝,梁文枭,王 强,孙正和
(1. 哈尔滨工业大学(威海) 光电科学系,山东 威海 264209;2. 河南理工大学 理化学院,河南 焦作 454000)
驻波能量及能流密度局部振荡理论探析
李爱芝1,梁文枭2,王 强1,孙正和1
(1. 哈尔滨工业大学(威海) 光电科学系,山东 威海 264209;2. 河南理工大学 理化学院,河南 焦作 454000)
以截面积为S密度ρ为的棒中沿相反方向传播的简谐横波叠加成的驻波为例,论证了驻波能量分布曲线和能流密度曲线都与驻波曲线相似.若将相邻波腹和波节间的各质元称为一段,分析表明,只有同一段中有能量转换和转移,且在半个周期内的能流密度等于零.这说明驻波中无单一方向的能流.
驻波;波腹;波节;能流密度
驻波是由振幅相同、频率相同、振动方向相同的两列简谐波,在同一直线上沿相反方向传播,叠加后形成的波.关于驻波的能量传播特性,许多文献已作了一些定量计算与讨论,但不太透彻.本文将对驻波中能量的转移与转换作进一步的深入探析,以使驻波的能量传播问题更便于理解,物理图像更加清晰.
1 驻波方程
设有两个振幅均为A,角频率为ω,波长为λ的简谐波,在同一x轴上沿相反方向传播.其波动方程分别为[1]:
y1=Acos(ωt-kx)y2=Acos(ωt+kx)
其中k=2π/λ,合成的驻波方程为:
y=y1+y2=2Acoskxcosωt
(1)
其中:cosωt表简谐振动,而|2Acoskx|就是简谐振动的振幅.
波腹(振幅最大的各点)位于:
(2)
波节(振幅为零的各点)位于:
(3)
介于波腹与波节之间的质点,它们的振幅则随位置坐标按|2Acoskx|的规律变化.
2 驻波的能量
在平衡位置为x处取一长度为dx的介质体元dv=sdx,其质量为dm=ρdv=ρsdx
此质元的振动动能[2]为:
dEk=2ρA2ω2sdxcos2kssin2ωt
(4)
此质元的弹性形变势能为[2]:
dEp=2ρA2ω2sdxsin2kxcos2ωt
(5)
此介质元的总能量:
dE=dEk+dEp=2ρA2ω2sdx(cos2kxsin2ωt+sin2kxcos2ωt) =ρA2ω2dv(1-cos 2kxcos 2ωt)
(6)由式(6)可看出,驻波的能量分布与式(1)中驻波的位移分布相类似,在空间有一个相对稳定的分布.
3 能流密度
由文献[3-4]知,两种简谐波的能流密度分别为:
I1=ρω2A2usin(ωt-kx),
I2=ρω2A2usin2(ωt+kx).
则合成驻波的能流密度为:
I=I1-I2=-ρω2A2usin 2kxsin 2ωt
(7)
由此可见,驻波的能流密度表达式也和驻波的位移相类似.
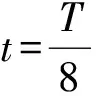
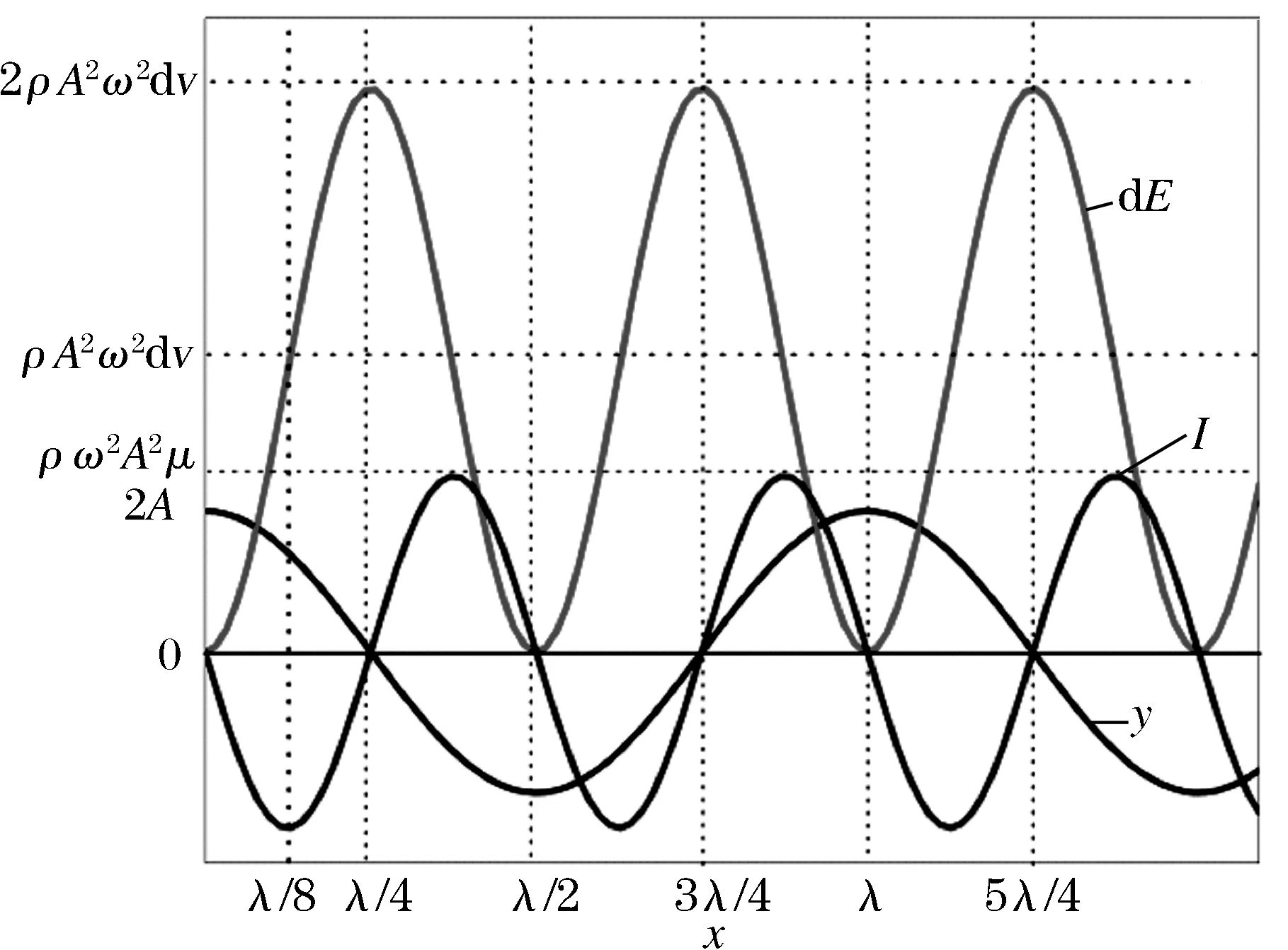
图1 位移(y)、能量(dE)和能量密度(I)随平衡位置(x)变化的曲线图
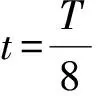
4 剖析驻波中质元能量的变化及流动
4.1 驻波波节处质元的能量[3]
由式(3)~(5)知
dEk=0,dEp=2ρA2ω2sdxcos2ωt
(8)
4.2 驻波波腹处质元的能量[3]
由式(2)、(4)、(5)知:
dEp=0,dEk=2ρA2ω2dvsin2ωt
数据显示,西北油田的“长子”西达里亚油田吨油操作成本由2015年的1704元大幅降至目前的626元,盈亏平衡油价由2017年的151.6美元/桶大幅降至目前的56.3美元/桶。
(9)

由此说明,波腹处的质元始终没有形变,势能为零,只有动能,且动能随时间作周期性变化,最小值为零,最大值为2ρA2ω2dv.
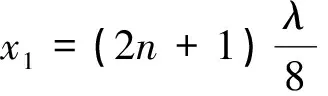
由式(4)、(5)知xi处质元的动能和势能分别为:dEk=ρA2ω2dvsin2ωt,dEp=ρA2ω2dvcos2ωt
则xi处质元的总能量为:
dE=dEk+dEp=ρA2ω2dv
(10)
4.4 相邻波腹和波节间质元的总能量
(11)
相邻波腹和波节间的总势能为:
(12)
(13)
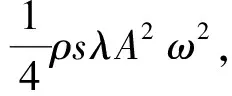
4.5 相邻波腹和波节间关于中心对称的两点的能量
dEr=ρA2ω2dv(1-sin 2kΔxcos 2ωt)
(14)
xi+Δx处质元的能量为
dEl=ρA2ω2dv(1+sin 2kΔxcos 2ωt)
(15)
以上两对称点的能量和
dEr+dEl=2ρA2ω2dv
(16)
式(14)~(16)说明,在相邻波腹和波节中,距离其中点相同的两点,向平衡位置运动时,靠近波腹的一点能量增加,另一点能量则等值减少.而远离平衡位置时则相反,但两点的能量之和在任意时刻都是不变的.
4.6 能流密度的变化
由能流密度的表达式(7)知,当
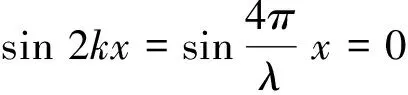
此时
(17)
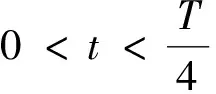
(18)
(19)
式(18)、(19)说明,驻波在任意半个周期内的平均能流等于零,能量只在相邻波腹和波节间来回振荡,并不向外传播.
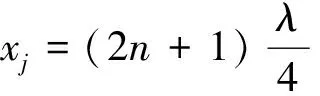
[1] 张三慧.大学物理学[M]. 北京: 清华大学出版社, 2011.151-157.
[2] 祝之光.物理学[M]. 北京: 高等教育出版社, 2009.318.
[3] 周世锟.对于驻波能量的定量研究[D]. 玉林: 玉林师范学院, 2012.8.
[4] 迟卓君, 孙艳梅, 梁法库. 解析驻波的能流密度[J]. 高师理科学刊, 2009, 29(2): 60-62.
Study on theory of wave energy and energy density of local oscillation
LI Ai-zhi1, LIANG Wen-xiao2, WANG Qiang1, SUN Zheng-he1
(1. Photoelectric Science Department, Harbin Institute of Technology (Weihai), Weihai 264209, China;2. School of Chemistry and Physics, Henan Polytechnic University, Jiaozuo 454000, China)
This paper focused on the standing wave formed by superposition of harmonic shear waves which propagated along the rod (the cross sectional area ofS, the mass density ofρ) in opposite directions. It demonstrated that the standing wave energy distribution curve and energy flow density curve were both similar as standing wave curve. If the matter element between adjacent wave loop and wave nodes was called a segment, the conversion and transfer of energy only occurred in the same segment, and the average energy flow density was equal to zero within half a cycle. The results showed that there was no single direction energy flow in standing wave.
standing wave; wave loop; wave section; energy flow density
2014-12-13.
山东省研究生教育创新计划(SDYY12005);哈尔滨工业大学(威海)大学物理精品课建设项目资助(ITGA10002003)
李爱芝(1969-),女,硕士,讲师,研究方向:大学物理.
O326
A
1672-0946(2015)03-0362-03

