输油管道表面裂纹初始扩展的研究

李若男，徐 莹， 杨银环，马有理

(哈尔滨商业大学 能源与建筑工程学院，哈尔滨 150028)

输油管道表面裂纹初始扩展的研究

李若男，徐 莹， 杨银环，马有理

(哈尔滨商业大学 能源与建筑工程学院，哈尔滨 150028)

针对输油管道中检测出的表面裂纹提出了在测量沿着裂纹表面的开口方向位移分布的基础上，通过计算裂纹周围的应力分布，评价裂纹端部应力强度因子Kest的方法.通过有限元解析对不同深长比(c/a)的表面裂纹，对在各种载荷作用下的应力强度因子KFEM进行了评价.并与传统的Newman-Raju公式对同样裂纹计算的相应应力强度因子K进行了比较.其结果是KFEM与K的结果基本相同.说明了本评价方法的可靠性.通过实验研究了表面裂纹初始疲劳扩展过程中裂纹端部应力强度因子Kest，结果表明对实际输油管道中存在的表面裂纹，即使载荷、裂纹深度未知及裂纹周围有残余压缩应力存在的情况下，本文提出的应力强度因子的评价方法仍然有效.

输油管道；表面裂纹；初始疲劳扩展；应力强度因子；开口位移

随着人们对能源需求的增加，已经建设并还将继续敷设大量的长距离输油管道，因此管道的断裂事故也屡有发生，往往造成灾难性的后果[1-2].对于服役期中的输油管道，不可避免地存在焊接质量、机械损伤、腐蚀等表面缺陷[3-4]—在管道的断裂破坏研究中可将其一律视为表面预裂纹.分析表明，除人为因素及自然灾害外，绝大部分的管道断裂破坏都是由上述的管道表面裂纹引起的[5].因此，针对表面裂纹研究者们已经进行了不少的有价值的研究工作[6-8].

但是以上的研究多是在裂纹的负荷为已知、同时表面裂纹的深度和裂纹的内部形状为已知的前提下进行的，而这对于使用中的输油管道中发现的表面裂纹而言是很难做到的.

裂纹的扩展特性可以用裂纹端部的应力强度因子来评价.对于贯穿的初始裂纹，通过测量裂纹的开口位移量,提出了裂纹周围的应力分布和裂纹尖端的应力强度因子的评价方法[9].本研究在此基础上，通过测量沿着表面裂纹的开口位移量，给出了沿着表面裂纹的应力分布的计算公式和表面裂纹尖端应力强度因子的评价公式.利用本文的评价方法对有限元(FEM)模拟结果进行了评价，同时与传统的Newman-Raju[10]的计算结果进行了比较，检验了本评价方法的可靠性.最后利用该方法通过实验研究了表面裂纹的初始疲劳扩展特性.

1 表面裂纹的应力分布和应力强度因子

在矩形板的中心部存在有长度2a，深度为c的表面裂纹，如图1所示.在板的两端(与裂纹垂直的y方向)作用有均布载荷б，按照本文3.2.1节的方法测量出在裂纹的任意位置的开口位移量V=v+-v-，则沿着表面裂纹的应力分布бest(x)可用式(1)表示[11].

(1)

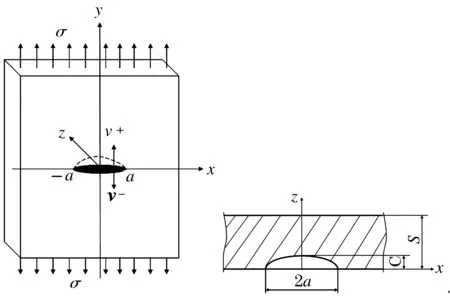
图1 表面裂纹开口位移

裂纹尖端处的应力强度因子Kest的计算方法如式(2)所示[11]

(2)

2 FEM解析

2.1 解析条件

为了检验本文中提出的应力强度因子计算方法的精确性，进行了如下的FEM模拟计算.首先表面裂纹的形状为如图1所示的椭圆形.有裂纹的矩形板的尺寸与3.1节中实验所使用的试件尺寸相同，即：宽度W=50 mm，长度H=180 mm，厚度S=6 mm.FEM计算时模型的要素分割如图2所示，模型为四结点要素,其裂纹端部的最小要素的尺寸为1 μm.与实验材料相对应,计算中材料的弹性模量取E=206 GPa，泊松比取ν=0.3.椭圆形裂纹的深度与长度之比c/a=0.5、0.6、0.8.在与裂纹垂直方向的模型两端施加б=120 MPa的均布载荷，进行了解析计算.

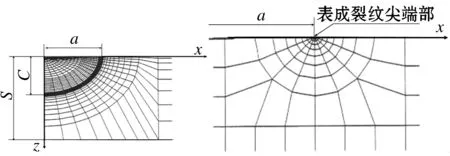
图2 表面裂纹的FEM计算模型

2.2 解析结果

对于单侧裂纹长度a=3.0 mm的表面裂纹，在载荷作用下其开口位移量如图3所示.图3中的横坐标是从裂纹中心开始的距离.图3中的虚线是按公式(3)计算的近似值[11].

(3)

其中：A、B、C和D为系数.在其他条件相同的情况下，随着表面裂纹深度值的减小，裂纹开口位移量降低，表明了裂纹深度对其开口位移量的影响.

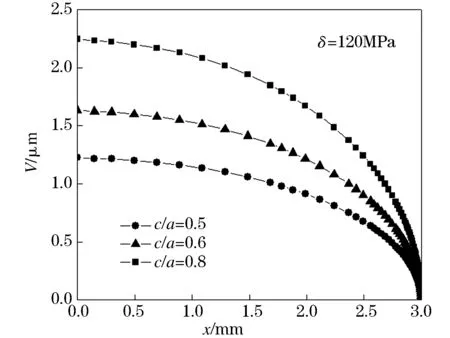
图3 FEM解析计算的表面裂纹开口位移量

将以上FEM解析结果的近似值V(x)代入公式(1)，得到的沿着裂纹的应力分布бFEM(x)如图4所示.与贯穿裂纹的бFEM(x)≈σ[11]相比，受表面裂纹深度的影响，沿着裂纹的应力分布бFEM(x)小于施加到模型上的载荷б，而且裂纹深度越浅，应力的计算值бFEM(x)越小.

最后将бFEM(x)代入式(2)，对有限元解析的表面裂纹端部的应力强度因子KFEM进行了评价.为了验证本文提出的应力强度因子的评价方法的可靠性，使用传统的Newman-Raju的式(4)[10]对相同的表面裂纹计算了应力强度因子K.KFEM与K两者的关系如图5所示.

(4)

其中：c为单侧裂纹的长度 (m) ；σ为施加的载荷 (MPa)；F、Q为系数.

由图5可知，由本文提出的评价方法计算得到的表面裂纹端部的应力强度因子KFEM与Newman-Raju公式的计算结果吻合的很好.因此在载荷及裂纹深度未知的情况下，利用本文的评价方法可以方便而准确地评价表面裂纹端部的应力强度因子.

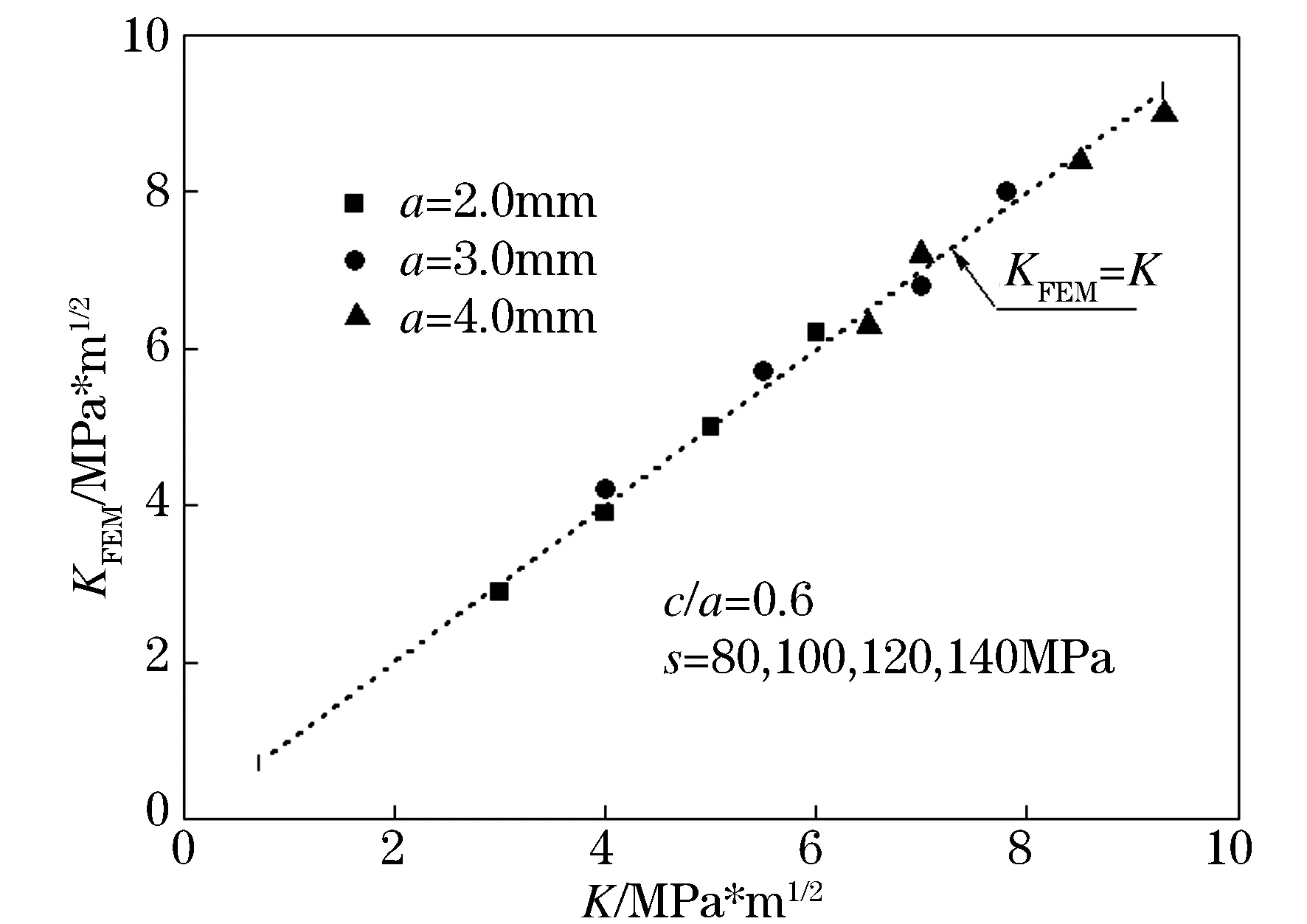
图5 应力强度因子KFEM和K的关系

3 表面裂纹的扩展实验

3.1 表面裂纹试件的制作

实验用材为输油管道用螺旋钢管材X45. 其机械性能如表1所示.

表1 钢管材料的机械性能

实验用矩形试件的尺寸如图6所示.为了在预定的位置产生表面裂纹的需要，在试件的中央开有非贯通的中心孔，其直径为1.0 mm，深度为1.0 mm.试件加工后为了实验过程中观察和测量的方便，试件中心部表面研磨光亮为止.

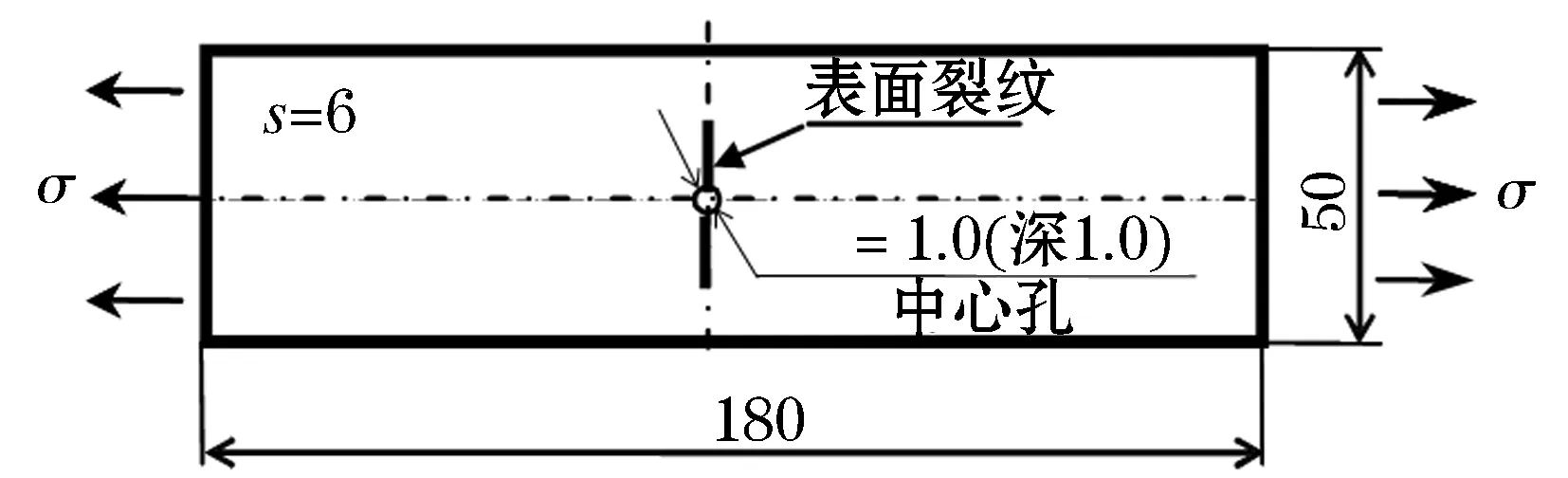
图6 带表面裂纹的试件

使用疲劳实验机对图6所示试件的载荷方向施加循环载荷，在试件表面中央位置处制作出了如图所示的实验所需的表面预裂纹.疲劳实验条件如下：脉冲疲劳实验机以加载频率20 Hz，应力比(最小应力与最大应力之比)R=0，最大应力值бmax=120 MPa的正弦波载荷进行疲劳试验，直到单侧裂纹长度a=2.02 mm疲劳实验结束.为了消除裂纹周围的残余应力，疲劳实验结束后对试件进行了退火热处理，其热处理温度为600 ℃，保温时间为1 h.

3.2 表面裂纹的初始疲劳扩展实验

对以上制作的表面预裂纹,仍然在疲劳实验机上以频率20 Hz，应力比R=0，最大应力值бmax=120 MPa的正弦波载荷进行了表面裂纹初始疲劳扩展实验.当裂纹扩展到不同的长度阶段，测量了沿着裂纹的开口位移量，据此对表面裂纹的疲劳扩展特性进行了考察.

3.2.1沿着疲劳扩展裂纹的开口位移量

沿着裂纹的张开位移量的测量是借助于放大倍数为100倍的光学显微镜进行的，如图7所示.

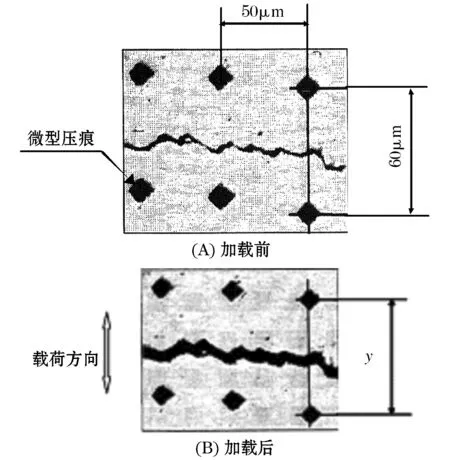
图7 沿着裂纹张开位移量的测量方法

在试件表面以裂纹为对称中心相距y0=60 μm，沿着裂纹两侧间距50 μm打印上成对的微小压痕如图7(A).每一对压痕在载荷作用下的距离为y，如图7(B).所以两者的差值V=y-y0既为该点处的裂纹张开方向的位移量.对每一对压痕进行如上的操作就可得到沿着裂纹全长的张开位移量的分布结果.

对单侧长度a=4.08 mm的表面疲劳裂纹，在б=80、100、120 MPa的恒定载荷分别作用下，沿着裂纹开口位移量的测量结果如图8所示.图8中的虚线仍然是按公式(3)计算的近似值.

图8 沿着表面疲劳裂纹的开口位移分布

3.2.2表面裂纹初始疲劳扩展过程中应力强度因子

对表面疲劳扩展裂纹的单侧长度分别为a=3.01、4.96 mm时，在同样的载荷б=80、100、120 MPa作用下，按照上面相同的方法测量了开口位移量.将以上开口位移量的近似值V(x)代入公式(1)，计算了沿着裂纹的应力分布бest(x)，再代入公式(2)，评价了裂纹端部的应力强度因子Kest.同时对同样的裂纹，在相同的条件下按式(4)的Newman-Raju公式计算了应力强度因子K.Kest与K的关系如图9所示.

由图9可知，疲劳扩展前的退火预裂纹(既图中的·)，其Kest与K相一致.但在裂纹疲劳扩展后，其评价得到的应力强度因子Kest比传统公式的计算值小很多，这可以认为是由于疲劳扩展过程中在裂纹周围产生的压缩残余应力对裂纹开口位移限制的结果.

因此，对于服役期的输油管道中发现的初始扩展阶段的疲劳表面裂纹，即使在载荷以及表面裂纹深度未知的情况下，通过测量沿着裂纹的张开位移量，即可正确地评价出裂纹端部的应力强度因子，从而可以实现不停输的管道剩余寿命的安全评价.

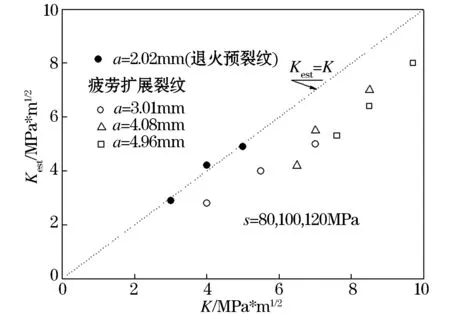
图9 由实验的表面裂纹计算的Kest和K的关系

4 结 论

服役期输油管道中检测出的表面裂纹(既非贯穿的表面缺陷)，如何评价其初始扩展特性，本文进行了研究和探讨，其结论如下：

1)提出了通过测量沿着表面裂纹的开口位移量，计算沿着裂纹的应力分布，进而进行表面裂纹端部应力强度因子评价的方法.

2)利用有限元对表面裂纹进行了模拟，并按照以上的方法评价了裂纹端部的应力强度因子KFEM，其值与根据Newman-Raju的传统公式对同一裂纹计算的应力强度因子K基本相一致.因此，在载荷及裂纹深度未知的情况下，使用本文的方法评价表面裂纹端部的应力强度因子是可行的.3)通过实验，评价了表面裂纹在初始扩展阶段的端部应力强度因子Kest.在裂纹疲劳扩展过程中的Kest值均低于Newman-Raju公式的计算值K，这正反映了表面裂纹疲劳扩展过程中裂纹周围的压缩残余应力对Kest的影响.

所以对于输油管道中存在的表面裂纹，在其初始扩展阶段，即使是受力及裂纹的深度未知的情况下,，可以通过本文提出的评价方法对裂纹端部的应力强度因子进行评价.

[1] 江 英, 赵新龙, 陈雪松, 等. 油浆管线弯头泄漏失效原因分析[J]. 管道技术与设备, 2013, 20(2): 4-6.

[2] 王予东, 肖志刚. 在役含缺陷油气管道的安全评价准则[J]. 油气储运, 2013, 32(6): 587-589.

[3] 周军华, 蒋永兴. 油气管道机械损伤引发事故与预防措施[J]. 油气储运, 2012, 31(2): 86-91.

[4] 姜信德, 李言涛, 杜芳林. 海底管线腐蚀与防护的研究进展[J]. 材料保护, 2010; 43(4): 65-67.

[5] 李平全. 油气输送管道失效事故及典型案例[J]. 焊管, 2005, 28(4): 76-92.

[6] 顾 乡, 吴志学. 新的估算表面裂纹应力强度因子经验公式[J]. 工程力学, 2008, 25(7): 35-39.

[7] 李国义, 郝丽丽, 李菁泉. 抽油杆杆体表面裂纹应力强度因子的研究[J]. 石油矿场机械, 2007, 36(12): 14-16.

[8] 暑恒木. 薄壁管道表面裂纹的应力强度因子计算[J]. 油气储运, 2001, 20(3): 25-26.

[9] 马有理. 油气输送管道疲劳裂纹起裂特性与影响因素[J]. 哈尔滨工程大学学报, 2012, 33(8): 984-988.

[10] NEWMAN J C, RAJU I S. An empirical stress-intensity factor equation for the surface crack[J]. Engineering Fracture Mechanics, 1981, 15(1): 185-190.

[11] MA Y L. Study on fatigue crack propagation behavior under mixed-mode conditions with compressive residual stress[M]. Tokyo: Parliament Library, 2006. 9.

Study on initial fatigue growth of surface-cracks detected from oil pipe line

LI Ruo-nan, XU Ying，YANG Yin-huan，MA You-li

(School of Energy and Civil Engineering, Harbin University of Commerce, Harbin 150028, China)

For surface-cracks detected from oil pipe-lines, a method to evaluate the stress intensity factorKestwas suggested by measuring the opening displacement distribution along the crack and calculating stress distributions around it. The stress intensity factorKFEMwas evaluated by FEM analysis for different ratio ofc/asubjecting various loading. The value ofKFEMwas compared withKcalculated by Newman-Raju’s conventional equation. The stress intensity factorsKFEMandKwere good agreement for all cracks. That is to say, the method suggested in this paper to evaluate the stress intensity factors is reliable.The stress intensity factorKestfor initial fatigue growth of surface-crack was studied by experiment. As a result, this suggesting method was also efficacious for the surface-cracks with residual stress detected from oil pipe-lines, even though the loading applied to the surface crack and the depth of it are unknown.

oil pipe line; surface crack; initial fatigue growth; stress intensity factor; opening displacement

2015-01-03.

黑龙江省教育厅科研项目(12521132)

李若男(1990-)，女，硕士，研究方向：石化设备与储运工程.

O346

A

1672-0946(2015)03-0300-04