基于ADC方法的地空导弹系统效能评估模型*1
基于ADC方法的地空导弹系统效能评估模型*1
王君,赵杰,邵雷,李进
(空军工程大学 防空反导学院,陕西 西安710051)
摘要:应用ADC方法建立了一种低空近程地空导弹武器系统效能评估的数学模型。分析了武器系统的可靠性逻辑结构,通过适当的计算假设,计算出武器系统的有效度矩阵;利用连续时间齐次马尔可夫链的柯尔莫哥洛夫向后方程和向前方程求解武器系统的可信赖度矩阵;选择武器系统的目标特性,射击能力,抗干扰能力,导弹能力和机动能力建立能力指数体系数学模型。仿真结果表明,方法具有较好的评估性能。
关键词:低空近程地空导弹;系统效能;ADC模型
0引言
武器装备效能指在规定的条件下达到规定使用目标的能力。效能度量分为3类:指标效能,系统效能和作战效能。指标效能是对各影响效能因素的度量;系统效能是由影响武器系统效能各因素综合而成的效能度量;作战效能是指在预期或规定的作战使用环境以及所考虑的组织、战略、战术、生存能力和威胁等条件下,装备完成规定任务的能力。对于装备的重大决策问题,应进行效能评估。在武器装备全寿命周期各阶段[1],为达到规定目标存在多种实现方案,且方案选择需要考虑各方案效能时,需要采用效能评估方法,以达到“优生、优育、优用”的目的。
对地空导弹武器装备系统效能评估的研究,从多年来查阅和收集的资料看,美国海军的Knut O. Flaathen[2]对防空导弹武器的系统效能进行了研究, 选取单发杀伤概率、系统反应时间、最大有效射程、导弹平均飞行速度、导弹价格等指标作为评价系统效能的主要因素,用加权求和法得到效能度量,然后进行多元回归分析建立武器性能指标与系统效能的函数关系;俄罗斯也采用简化的评价武器效能方法,如俄罗斯安泰设计局评价地空导弹武器效能,便选择多个类似型号,比较它们的若干相关参数,如最大射高、最小射高、最大射程、单发杀伤概率、目标最大速度、目标最大过载、目标通道数、导弹连装数和反应时间等,采用连乘和归一化方法,比较它们的能力。也有其他一些学者提出了概率模型[3]、模糊排队模型[4]、通用模型[5]等进行系统效能评估的研究,但这些研究的简化评价方法在选取影响系统效能的因素时,考虑过于简单,不能全面地评价地空导弹武器装备的系统效能。
在国内,一些学者分别采用证据理论[6-7]、模糊评估[8-9]、排队论[10-11]等方法针对武器装备系统效能评估进行了深入研究。以上述研究为借鉴,本文在研究中,选择武器系统的目标特性,射击能力,抗干扰能力,导弹能力和机动能力基于ADC方法建立地空导弹系统效能评估模型。
1地空导弹武器装备系统效能评估概念模型
目前,围绕装备系统效能问题,国内外专家已经提出了许多评估方法,其中一些方法已在实践中被广泛采用[12-13]。
地空导弹武器是一种反空袭、反空中侦察的武器,它作为一个分系统,无论平时和战时,都在图1所示的2种状态中循环。
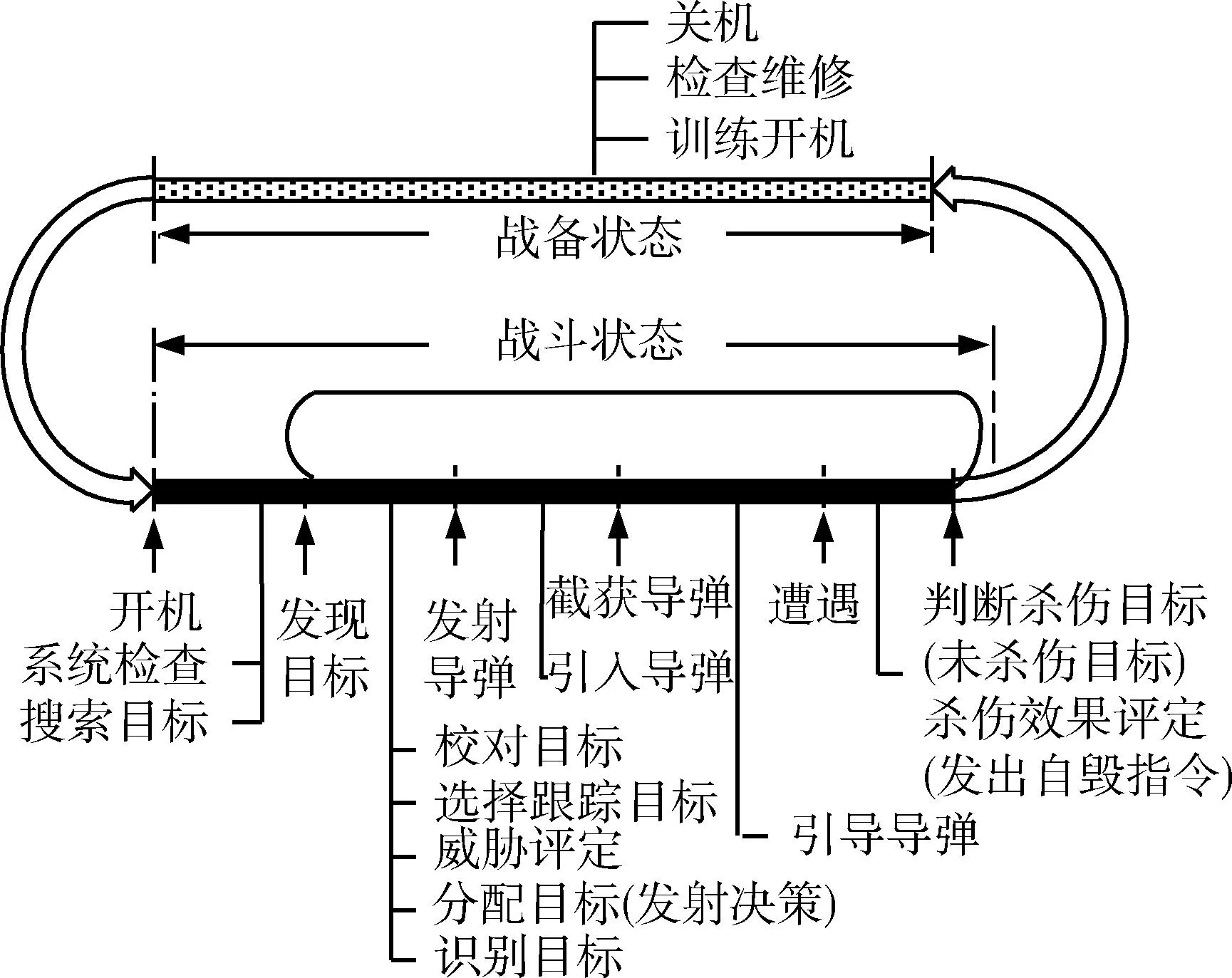
图1 地空导弹火力单元战备、战斗循环Fig.1 Preparation and fight circle of ground to air missile fire unit
战备状态可用有效度进行度量;战斗状态则应由2种要素度量:一是可靠度,二是能力。前者表示执行战斗任务过程中保持武器良好的程度;后者表示当武器在战斗中良好时,完成任务的程度。因此,采用A,D, C 3个要素综合描述地空导弹武器的效
能是合理的,图2表明了效能三要素的构成因素。

图2 地空导弹系统效能要素构成Fig.2 Factors composition of the ground to air missile system effectiveness
有效度是指开始执行任务时武器系统所处状态的概率。有效度是一个行向量,考虑地空导弹武器由多个分系统组成,可通过计算地空导弹武器系统处于各种状态的概率进行研究。
可信赖度是指已知开始执行任务时系统的状态,且执行任务中系统可能处于或进入任一有效状态,完成与这些状态关联任务的概率。可由不同可靠度元素组成的矩阵表征。
能力是指已知武器系统在执行任务过程的状态,该系统完成规定任务要求能力的量化表征。它应当反映出武器的基本性能、作战范围、适应的战场环境等。
2地空导弹武器系统效能评估数学模型
2.1效能评估数学模型的基本形式
根据概念模型,地空导弹武器的系统效能(E)含有有效度(A)、可信赖度(D)和能力(C)三大要素。而有效度、可信赖度和能力分别用A矩阵、D矩阵和C矩阵表示,即
A=(a1,a2,…,an);D=(dij)n×n;C=(c1,…,cn)T,
(1)
式中:ai(i=1,2,…,n)为开始执行任务时武器处于i状态的概率;dij(j=1,2,…,n)为已知武器系统在i状态开始执行任务,执行任务中处于j状态的概率;cj(j=1,2,…,n)为武器系统处于状态j时具备的能力指数。
上述三要素在效能中应呈现链状逻辑,即有效度、可信赖度和能力其中任一项为0时,武器系统的效能则为0,而表达这种链状逻辑的数学模型是乘积关系,即
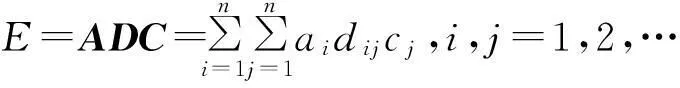
(2)
2.2有效度矩阵
有效度矩阵A,是一个行向量(a1,a2,…,an)。建立一个地空导弹武器的有效度向量,必须从分析其结构与可靠性特征量人手。分析目前世界上典型的低空近程地空导弹武器系统,其可靠性逻辑结构如图3所示。

图3 低空近程地空导弹的典型可靠性逻辑结构Fig.3 Typical reliability logic structure of the low height and short range ground to air missile
图中,AU为搜索指挥单元;FUi(i=1,2,…,n)为发射单元,n≥3。
由于每部车都有2种状态,即正常状态和故障状态,因此,理论上讲,武器系统的状态数应为2M,M为图3中考虑的车辆的总数,并不包含武器系统其他车辆(如通信车、电源车、维修车等)。可见,若考虑武器系统所有状态数,则有效度向量A的维数非常大,计算十分复杂,状态数过大时,也导致可信赖度矩阵D无法计算。因此,必须对武器系统的状态进行简化处理,一方面保证能满足计算需求,另一方面又要保证尽可能对效能评估结果有最小的影响。
假定武器系统内同时出现故障的车辆数最多不超过3辆。经分析,给出武器系统开始执行任务时所处的状态空间,如表1所示。
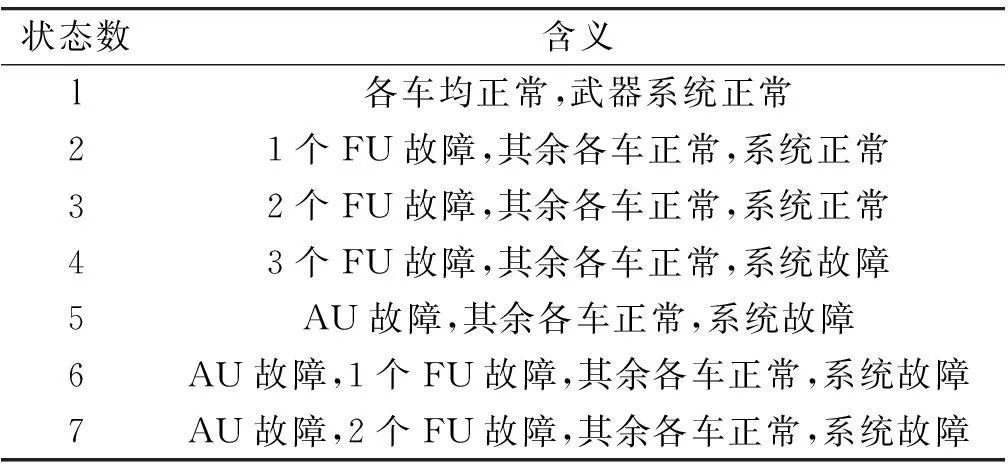
表1 武器系统的状态
搜索指挥单元(AU单元)的有效度aAU为
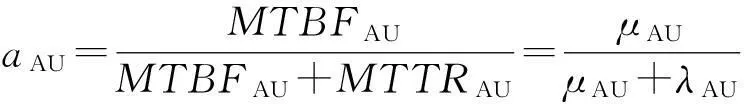
(3)
式中:MTBFAU,λAU为AU单元平均无故障时间和故障率,λAU=1/MTBFAU;MTTRAU,μAU为AU单元故障平均修复时间和维修率,μAU=1/MTTRAU。
同理可得发射单元(FU单元)的有效度aFU。
这样可计算出武器系统的有效度矩阵A=(a1,a2,…,a7)。
2.3可信赖度矩阵
如果开始执行任务时武器系统有n种状态,武器系统在执行任务后任意时刻处于某种状态可看作是一个随机过程。根据可信赖度的概念模型,则可信赖度矩阵是一个n阶方阵,即D=(dij)n×n。在确定矩阵中的元素dij(i,j=1,2,…,n)时,不考虑维修,因为作战中武器系统不能维修。这样,其状态转移可用连续时间马尔可夫链来解决。
基于连续时间马尔可夫理论可知,若知道武器系统中每一个分系统的故障分布,就可计算出在任务时间t后系统的转移概率矩阵P(t),有效度矩阵D=P(t)。
假定武器系统中各分系统的故障服从指数分布规律,即
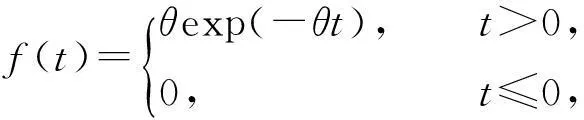
(4)
式中:θ为故障率参数;f(t)为概率密度函数。
在计算Q矩阵时,为了简化计算,这里假定武器系统在一个Δt的工作时间内(Δt→0),同时出现2个设备故障的可能性非常小,可以近似为0,这种假设也符合实际情况,可大大减小计算复杂度。基于上面假定,下面分析武器系统的Q矩阵,并求解有效度矩阵D。
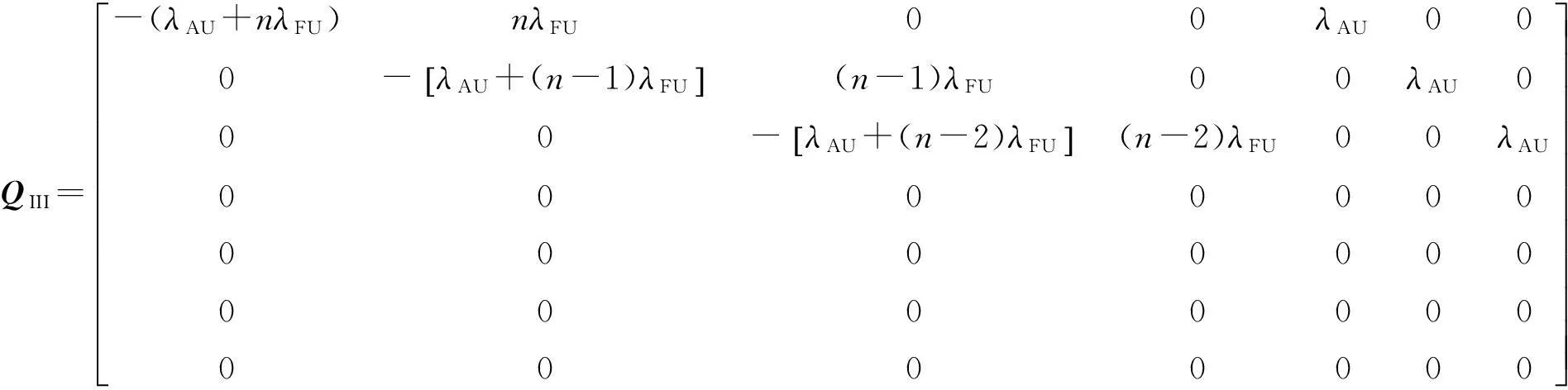
(5)
P(t)矩阵元素为(只列举几个公式,其余略):
p11(t)=e-(λAU+nλFU)t;p12(t)=ne-(λAU+(n-1)λFU)t-ne-(λAU+nλFU)t;
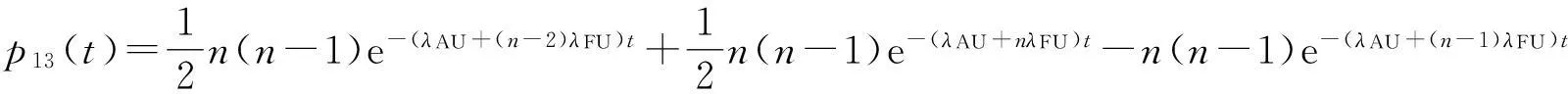
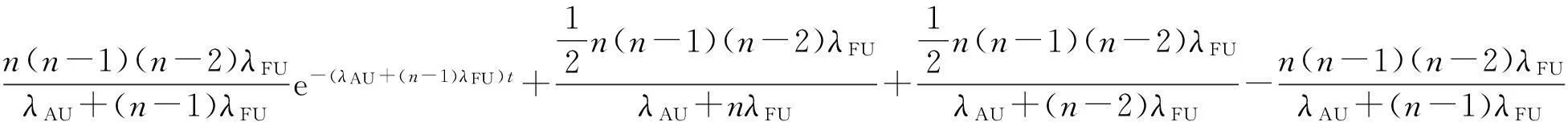
2.4能力矩阵
根据能力的概念模型,采用下面能力指数体系数学模型
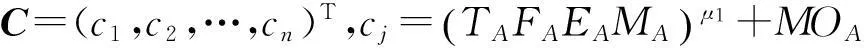
(6)
式中:cj为武器系统处于状态j时具有的能力指数;TA为目标特性指数;FA为射击能力指数;EA为抗干扰能力指数;MA为导弹能力指数;MOA为机动性指数;μ1为常数。
2.4.1目标特性指数
所谓目标特性是指武器系统能拦截的目标类型、速度、机动能力和雷达反射面积等。目标特性指数TA的数学模型为
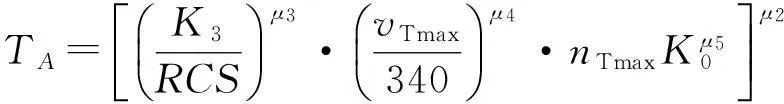
(7)
式中:RCS为典型目标的雷达反射面积,m2;vTmax为典型目标最大飞行速度,m/s;nTmax为目标最大机动过载,无量纲;K0为目标种类,无量纲;K3,μ2,μ3,μ4,μ5为常数。
可见,可拦截的目标RCS越小,vTmax越大,nTmax越大和目标种类K0越多,说明武器系统拦截的目标特性越好,武器系统的能力越强。
2.4.2射击能力指数模型
影响地空导弹射击能力的主要因素有反应时间、杀伤区、火力强度和单发杀伤概率等。射击能力指数FA的数学模型为

(8)
式中:Tr为武器反应时间;KL为杀伤区因子;FR为火力强度因子;p为单发杀伤概率因子。
通过分析可知,武器系统的反应时间Tr越小,杀伤区因子KL,火力强度因子FR,单发杀伤概率因子p越大,射击能力指数就越大。
杀伤区因子KL数学模型为

(9)
式中:Hmax为高界(与目前地空导弹武器最小高界比较);Hmin为低界(与目前典型的低界比较);Rmax为远界(与目前最小的远界比较);Rmin为近界(与目前典型的近界比较);εmax,qmax为最大高低、航路角(与目前典型值比较),(°);μ7,μ8为常数。
可见,杀伤区高界越高、低界越低、远界越远、近界越小及拦截的目标最大高低角、最大航路角越大,武器系统的杀伤区因子就越大。μ7为将杀伤区高、低、远、近界和最大高低角、航路角进行均衡的常数,μ8为将杀伤区因子与射击能力指数中其他因子均衡的常数。
火力强度因子FR的数学模型为
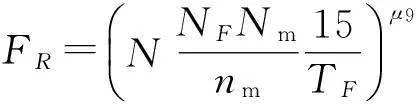
(10)
式中:N为目标容量,无量纲;NF为发射装置数量,无量纲;Nm为每套发射装置上的装弹数,无量纲;nm为射击一个目标最多同时发射的导弹数,无量纲;TF为导弹装填时间;μ9为均衡火力强度因子与射击能力指数其他因素的常数。
可见,目标容量越大及发射装置数、单套发射装置上装弹数越多,火力强度因子就越大;而射击单个目标要求的导弹数越多及向发射装置装填导弹的时间越长,火力强度因子越小。
单发杀伤概率因子为
p=K2p1,
(11)
式中:p1为导弹单发杀伤概率;K2为常数。
2.4.3抗干扰能力指数模型
抗干扰能力是地空导弹武器极重要的战术技术指标,在复杂的电子战环境中,地空导弹武器能否有效地拦截目标,已成为世界各国对地空导弹武器的关键要求之一。建立地空导弹武器抗干扰能力模型,又是一件极其困难和复杂的事情。地空导弹武器在作战过程中,从始至终以电磁信息的多环节传递、处理为生命线,在传递、处理的任一环节中信息发生畸变,都会降低武器系统的效能,甚至破坏其正常工作。根据地空导弹武器工作和结构特点,把与抗干扰有关的工作分为3个阶段,每个阶段可能有4种互相区别的抗干扰能力(量化的),见表2所示(打“√”为相应阶段中有该因子)。
基本抗干扰因子(BE),是指探测、跟踪雷达的发射功率和分辩力。不论抗消极干扰、抗压制式干扰和回答式干扰,提高发射功率和分辨力都是最基本的方法。

表2 地空导弹的3个工作阶段
增强抗干扰因子(AE),是指对某类或一、二类干扰采取措施引起武器系统抗干扰能力的增加量。
工作体制因子(RE),是指对武器的探测、跟踪、制导装置采用不同工作体制时抗干扰能力的评价值。
制导体制因子(GE),是指采用不同制导体制时,使制导阶段抗干扰能力基本增加量。
抗干扰能力指数为

(12)
式中:S为搜索因子;T为跟踪因子;G为制导因子;μ10为其他因素均衡常数。
搜索因子

(13)
式中:BE为基本抗干扰因子;AE为增强抗干扰因子;RE为雷达工作体制因子;μ11为常数。
基本抗干扰因子由雷达发射功率与综合分辨力决定,经研究,可得到达基本抗干扰因子为
BE=PP·BS·TC·G/10,
(14)
式中:PP为雷达发射功率;BS为信号带宽,MHz;TC为雷达信号照射时间;G为天线增益。
增强抗干扰因子AE的取得,应列出武器系统采用的抗干扰措施。
雷达工作体制因子RE的取得,也根据其工作体制赋值得到。
跟踪因子
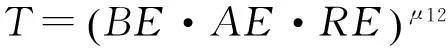
(15)
式中:BE,AE,RE为基本抗于扰因子、增强抗干扰因子、雷达工作体制因子,其值和搜索因子相同;μ12为常数。
2.4.4导弹能力指数模型
导弹能力主要考虑导弹的过载能力(可用过载)、速度特性和发动机工作时间等,模型中没计及战斗部杀伤半径、引战配合概率等,因为它们不是独立要素,在单发杀伤概率中已考虑过。导弹能力指数模型为
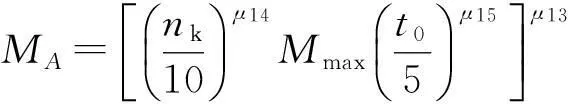
(16)
式中:nk为可用过载(与典型值10比较);Mmax为导弹最大速度;t0为发动机工作时间(与最小工作时间为5 s比较);μ13,μ14,μ15为常数。
可见,导弹的可用过载、最大速度及发动机工作时间越大及越长,导弹的能力指数就越大。
2.4.5机动性指数模型
地空导弹武器系统的机动能力与展开时间、撤收时间、最大行军速度、最大行军里程及越野性、可运输性等指标有关,其中可运输性不是独立的要素,因为其他几项机动性指标已经包含了武器系统可运输性的信息,故将可运输性指标略去。略去越野性因素,建立的机动性指数MOA数学模型为

(17)
式中:Dt为展开时间(与典型展开时间15 min比较);Wt为撤收时间(与典型撤收时间6 min比较);vmax为最大行军速度(与典型行军速度25 km/h比较);MR为最大行军里程(与典型最大行军里程500 km比较);μ16,μ17,μ18为常数。
2.4.6能力数学模型系数的确定
综合反映武器系统能力的若干要素分为不同层次,如图2所示。能力矩阵中的要素构成层次分析结构模型。由于层次间元素的联系比同层次各元素间联系强得多,因此摒弃同层次元素间的关联,因而武器系统能力的递阶层次结构是单准则的。
能力模型中的系数,采用多准则决策中常用的层次分析法(analytic hierarchy process,AHP)来解决。其步骤如下:
(1) 分析武器系统效能各要素间关系,建立武器系统效能递阶层次结构;
(2) 对同层各元素关于上层次中某一准则的重要性进行两两比较,构造两两比较判断矩阵,并计算被比较元素对该准则的相对权重:
(3) 计算各层次元素对能力目标的合成权重,并进行排序,依次得模型中的系数。
关于如何应用AHP方法确定能力模型中的系数,请参考相关文献,这里不再赘述。
3应用算例
欲对某型地空导弹武器系统进行改进,以提高武器系统的作战效能,利用效能评估模型对原型系统(A型)和改进型系统(B型)进行效能评估和对比,为战术技术指标的论证提供科学的依据,地空导弹武器系统基本性能参数列于表3。
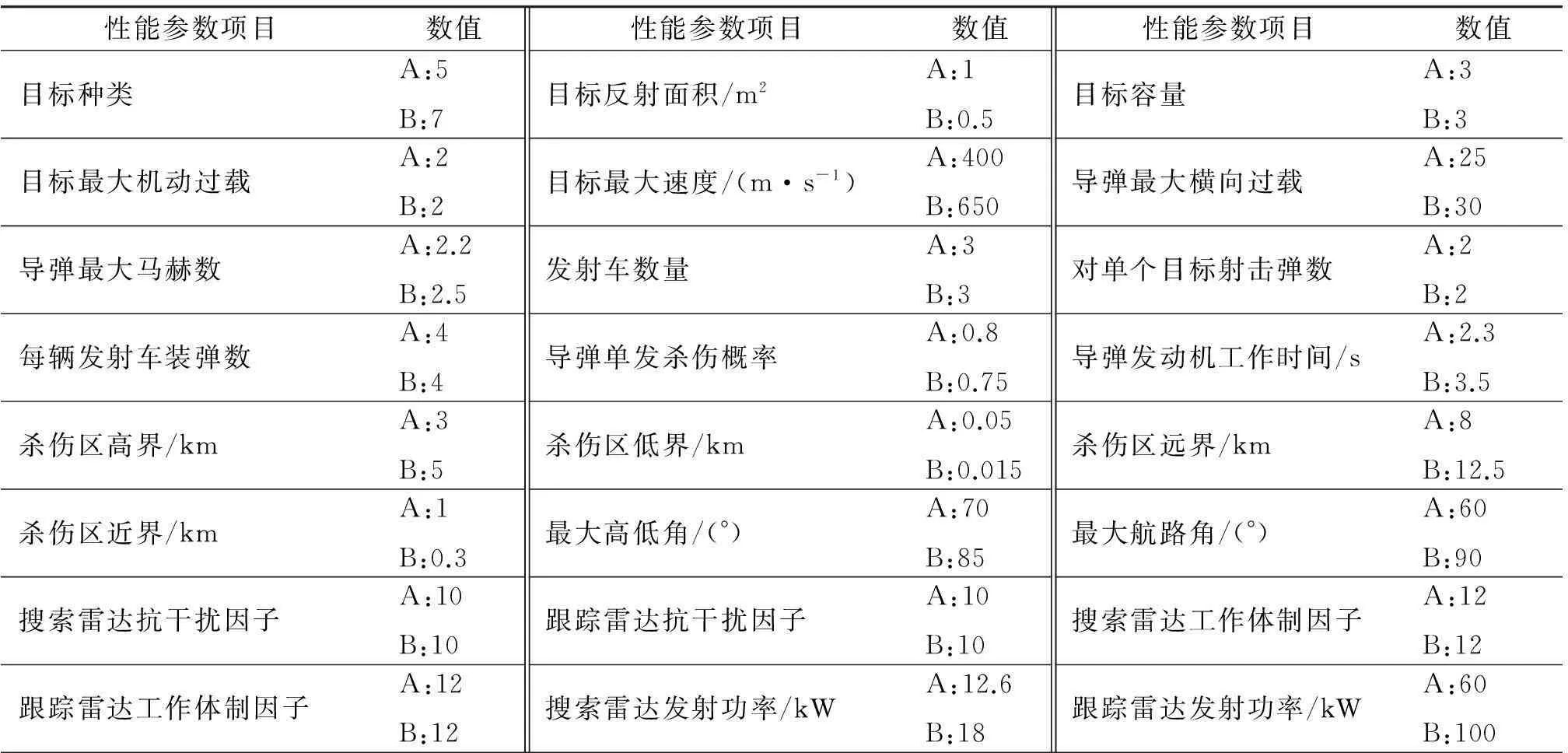
表3 武器系统基本性能参数
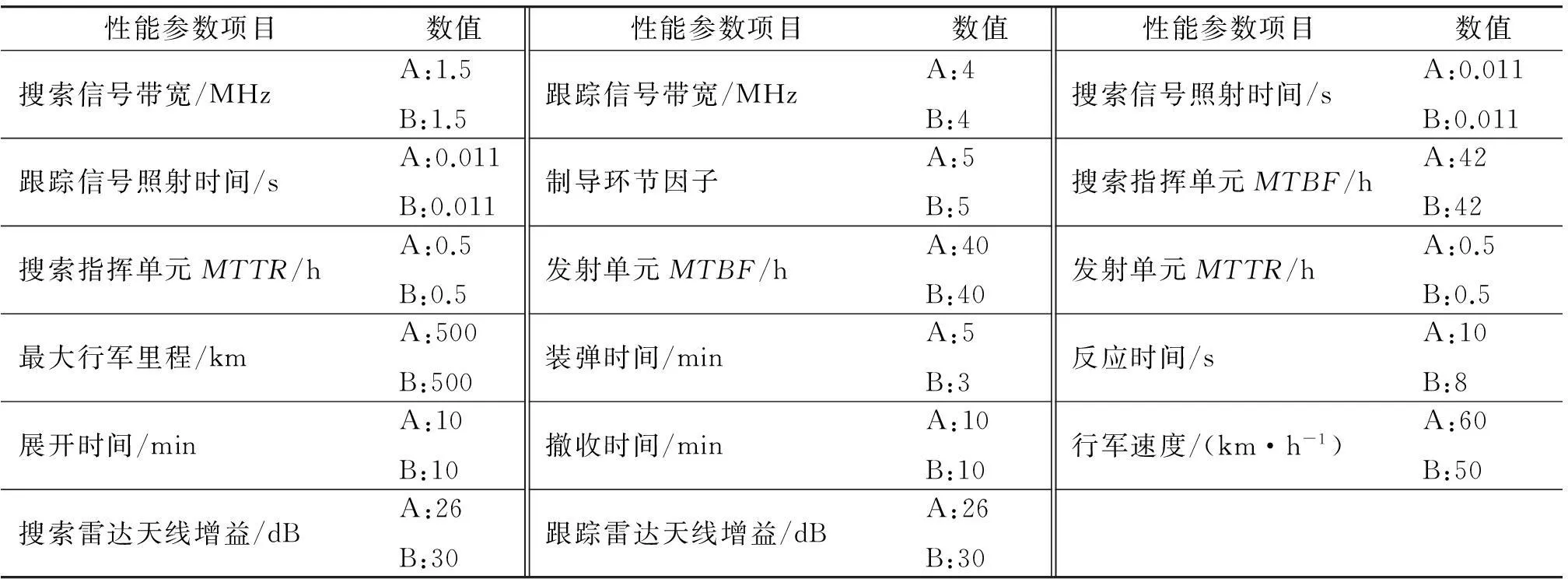
续表3
能力模型系数取值为:K1=81,K2=100,K3=3,μ1=0.34,μ2=0.65,μ3=0.25,μ4=1,μ5=0.5,μ6=0.15,μ7=0.6,μ8=0.75,μ9=1,μ10=0.25,μ11=0.45,μ12=0.5,μ13=1.5,μ14=0.58,μ15=0.35,μ16=1.25,μ17=1.34,μ18=1.24,μ19=0.5。
系统效能评估结果列于表4。由评估结果可见,在对原型系统部分战术技术指标改进的基础上,系统效能可提高大约44.6%。
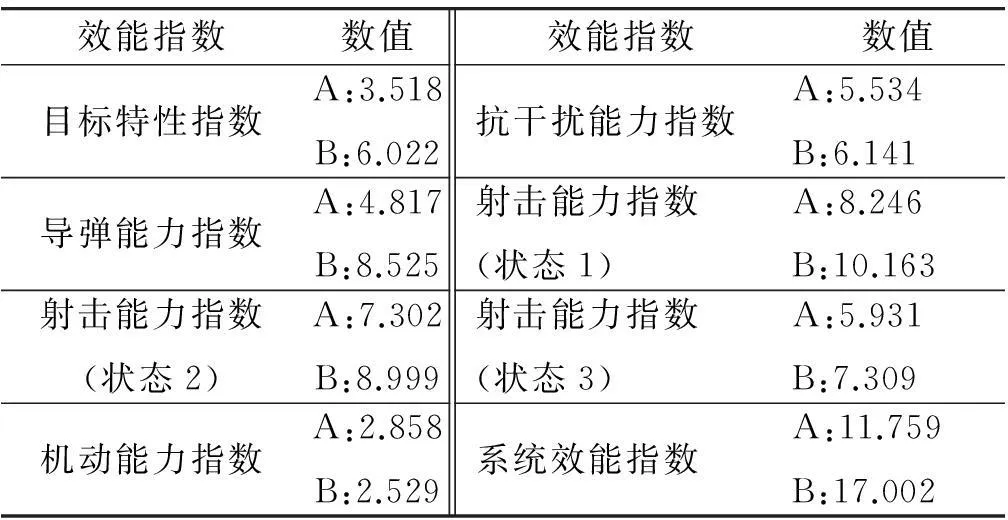
表4 效能评估结果
4结束语
ADC方法是目前评价武器装备系统效能的标准方法,可方便的分析复杂武器系统的效能,因此在实践中得到了广泛应用,WSEIAC针对不同的情况还提出了几个修正模型,如ARC模型、QADC模型、KADC模型、CADS模型等,均可尝试用于地空导弹武器装备系统效能评估。
目前地空导弹武器的作战适用性问题引起各国军方的重视,美国、俄罗斯等军事大国都在实施一系列改善武器系统作战适用性计划,以提高武器的效能。作战适用性是指武器在作战环境中使用的良好程度,它受武器的可靠性、维修性、测试性、保障性、可用性、安全性、兼容性及互用性等多种因素的综合影响,是影响武器系统作战能力的关键要素之一。由于测试性、保障性、安全性、兼容性及互用性等,目前尚没有简便、有效的定量表示方法,因此,将它们引入地空导弹武器系统效能要素中来还有待进一步的研究。
在ADC模型中,计算有效度时为了计算方便,我们假定各分系统只考虑有2种状态:工作状态和故障状态。但实际武器系统可能处于若干个明显划分的工作状态,如何有效处理计算复杂度问题目前仍没有很好的方法解决。计算有效度必须考虑预防性维修(保养)时间和其它停机状态,还必须考虑维修程序、人员配备、备件供应、运输和各种行政管理措施等,但目前尚无简便易行的方法,还有待进一步研究。
参考文献:
[1]KEENEY R L.,RAIFFA H. Decisions with Multiple Ojectives: Preferences and Value Tradeoffs[M].New York:Wiley, 1976:32-49.
[2]Knut O Flaathen. A Methodology to Find Overall System Effectiveness in a Multicriterion Environment Using Surface to Air Missile Weapon Systems as an Example[D]. Monterey, California:Naval Postgraduate School,1981.
[3]SONG S J. Probability Models for Assessing the Value of Battle Damage Assessment in the Defense Against Equential Theater Missile Attacks[R]. ADA311138.
[4]KULAK O, KAHRAMAN C. Fuzzy Mufti-Attribute Selection Among Transportation Companies Using Axiomatic Design and Analytic Hierarchy Processs[J]. Information Sciences, 2005, 170(24): 191-210.
[5]RICHARD C C, ILVAS M T. A Generic Model of Equipment Availability Under Imperfect Maintenance [J]. IEEE Transaction on Reliability, 2005, 54 (4): 564-571.
[6]JIANG Jiang, LIAO Xuan, ZHOU Zhi-jie, et al. Weapon System Capability Assessment Under Uncertainty Based Onthe Evidential Reasoning Approach[J]. Expert Systems with Applications,2011, 38(11): 3773-3784.
[7]齐照辉, 刘雪梅, 梁伟. 基于证据理论的导弹对抗防御雷达作战效能评估方法[J]. 系统工程理论与实践, 2010, 30(1): 173-177.
QI Zhao-hui, LIU Xue-mei, LIANG Wei. Combat Effectiveness Evaluation Method for Missile Confronted with Radar Based on Evidence Theory[J]. Systems Engineering-Theory & Practice, 2010, 30(1): 173-177.
[8]齐照辉,刘雪梅,梁伟,等. 基于分层赋权的导弹防御效能模糊评估方法[J]. 系统工程理论与实践, 2011, 31(9): 1811-1815.
QI Zhao-hui, LIU Xue-mei, LIANG Wei, et al. Fuzzy Evaluation Approach to Missile Defense Effectiveness Based on Layered Weight Coefficients[J]. Systems Engineering-Theory & Practice, 2011, 31(9): 1811-1815.
[9]Ying Chyi Choua, Chia Chi Sunb, Hsin Yi Yen. Evaluating the Criteria for Human Resource for Science and Technology (HRST) Based on an Integrated Fuzzy AHP and Fuzzy DEMATEL Approach[J]. Applied Soft Computing, 2012, 12(1):64-71.
[10]王必达, 连一峰. 一种基于排队论的DoS攻防绩效评估方法[J]. 中国科学院研究生院学报, 2010, 27(1): 107-116.
WANG Bi-Da, LIAN Yi-Feng. An Efficiency Evaluation Methodology of DoS Attack and Defense Mechanisms Based on Queueing Theory[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2010, 27(1): 107-116.
[11]Behnam Vahdani, Reza Tavakkoli-Moghaddam, Fariborz Jolai. Reliable Design of a Logistics Network Under Uncertainty: A Fuzzy Possibilistic-Queuing Model[J]. Applied Mathematical Modelling, 2013, 37(5):3254-3268.
[12]KOU Hong-chao, WANG Jun-yong, LI Sheng-jie. Effectiveness Evaluation of Command Information of Command Information System Operation Based on Hierarchy-grey Analytic Method[J]. Ship Electronic Engineering, 2012, 32(2): 77-81.
[13]JIA Wen-long,LI Chang-jun, WU Xia. Application of Multihierarchy Grey Relational Analysis to Evaluating Natural GasPipelne Operation Schemes[J]. Adanced Research on Computer Science and Information Engineering, 2011, 152: 226-330.
System Effectiveness Evaluation Model of Ground to Air Missile Based on ADC Method
WANG Jun, ZHAO Jie, SHAO Lei, LI Jin
(AFEU,Air and Missile Defense College,Shaanxi Xi′an 710051, China)
Abstract:A system effectiveness evaluation model of the low height and short range ground-to-air missile is established with the application of ADC method. Typical reliability logic configuration is analyzed, availability matrix of weapon system is worked out with the appropriate computation hypothesis. Dependability matrix of weapon system is solved by using Kolmogorov backward and forward equations of the continuous time homogeneous Markov chain. The mathematical model of capability exponent system is established by selecting target characters, firing capability, anti-jamming capability, missile capability and mobility capability. A application example shows the effectiveness of the proposed model.
Key words:low high and short range ground to air missile; system effectiveness; availability dependability capacity (ADC) model
中图分类号:TJ762.1+3;E920.8
文献标志码:A
文章编号:1009-086X(2015)-06-0013-08
doi:10.3969/j.issn.1009-086x.2015.06.003
通信地址:710051陕西西安灞桥区长路东路甲字一号E-mail:wangjun197618@163.com
作者简介:王君(1975-),男,吉林东丰人。副教授,博士,主要研究方向为反空反导武器系统总体技术。
*收稿日期:2014-06-08;修回日期:2014-10-10

