基于NSGA-Ⅱ的伺服系统控制参数多目标优化设计

武 飞，段丽华，张昆峰

(中国空空导弹研究院，河南 洛阳471009)



基于NSGA-Ⅱ的伺服系统控制参数多目标优化设计

武 飞，段丽华，张昆峰

(中国空空导弹研究院，河南 洛阳471009)

针对采用分段式PID控制策略的伺服系统控制参数设计周期长、成本高的问题，提出一种基于快速非支配排序遗传算法(NSGA-Ⅱ)的控制参数多目标优化设计方法。在建立某型伺服系统仿真模型的基础上，选择各区间的PID控制参数为优化变量，以伺服控制系统的3个性能指标作为优化目标，寻找伺服系统控制参数的最优解，并进行仿真与实物实验验证。结果表明，设计的控制参数可以满足伺服控制系统的性能指标要求，大大缩短设计周期，节约设计成本。

分段式PID控制策略；伺服系统；快速非支配排序遗传算法；多目标优化设计

0 引言

在传统的伺服系统设计方法中，通常是依据专家经验，经过反复试凑和修正才能最终确定和匹配系统的控制参数，导致产品的研制周期长，研制成本高；同时，由于系统验证受制于试验方法和测试手段的完备性，无法使设计的产品得到充分的验证，其设计仍可能存在进一步优化的余地，难以达到产品设计的最优化。

目前，得益于计算机技术的快速发展，在计算机仿真的基础上，使用优化算法对控制参数进行优化调整，已经成为了一个研究热点[1-2]。但是，由于伺服系统的稳定性、信号跟随特性和调节时间等控制目标存在相互排斥及制约的关系，即便采用成熟的单目标优化算法进行优化，往往也很难得到理想的解决方案。因此，国内一些专家学者对于使用多目标优化方法优化调整控制参数进行了一定的探索和尝试[3-5]。

本文基于分段式PID控制策略建立了某型伺服控制系统的仿真模型，并引入基于NSGA-Ⅱ进行了系统控制参数的多目标优化设计。对所得的控制参数进行仿真，仿真结果证实了该方法的有效性。

1 伺服控制系统

随着数字电子技术和无刷电动机技术的快速发展，数字式无刷电动伺服系统已逐渐成为小型伺服系统的首选。某型数字式无刷电动伺服系统具有输出功率大、快速性好，工作时间更长等优点，其主要由伺服电机、减速机构、角位移反馈回路、DSP控制电路、逻辑综合电路及驱动电路组成，其工作原理如图1所示。

图1 伺服系统工作原理Fig.1 Principle of servo system

其中，伺服系统控制器(即DSP电路)接收上级控制系统传输来的伺服控制指令，综合反馈回路根据角位移计算出的反馈电压在数字处理芯片中按照控制算法进行处理，输出脉宽调制信号(PWM波)和电机转向控制信号。将这两个信号经信号处理后，与电机反馈回的霍尔信号共同输入逻辑综合电路产生驱动信号，并通过驱动电路作用驱动伺服电机按照特定方式转动。电机带动减速机构在输出轴上形成一定的角位移，满足控制需要。

2 伺服控制系统仿真建模

根据某型伺服系统的工作原理及相关参数，在Matlab/Simulink中建立系统的仿真模型，并设置相应的驱动电路及电机模型参数。根据伺服系统输出端偏转角度的极限限位与电压信号的幅值设置比例环节，以代替角位移反馈装置的作用。其中，PWM调制信号为12.5Hz，系统采样周期为5μs，电机的单相绕组R=1.5Ω，单相绕组电感H=1mH，反电动势常数Ke=0.054V/(rad·s)，电机转动惯量J=4.146×10-6kg·m2。仿真模型中的减速机构及控制算法设计过程如下。

2.1 伺服控制系统减速机构建模

某型伺服控制系统减速机构原理如图2所示。电机转动时，带动减速齿轮使丝杠旋转，螺母根据丝杠的旋转左右移动，带动摇臂偏转，使输出轴转动形成角位移。

图2 某伺服系统减速机构原理图Fig.2 Principle of retarding mechanism

根据减速机构原理图可计算出减速机构的减速比为

(1)

其中，Z=θm/θ为减速齿轮的减速比，r为输出轴中心距丝杠的垂直距离，P为滚珠丝杠的导程，γ为输出轴的偏转角度。

由于丝杠长度远小于输出轴中心距丝杠的垂直距离，所以，可将减速机构的减速比近似看作一个线性比例环节，其仿真结果并不影响对系统性能指标的判断。代入相关数据后得出减速机构的减速比Rate=173。

针对伺服系统中的非线性环节包括摩擦、黏性阻尼作用，减速机构的动力学方程如下

(2)

其中，M为电机的输出电磁转矩，θ为电机的输出角度，即减速机构的输入力矩，J为折算到电机轴的总转动惯量，k为黏度系数，Mc为动摩擦力矩，这里仅考虑动摩擦因素。

减速机构中的传输间隙则采用传输时延环节进行模拟。

2.2 伺服系统控制算法

由于该型伺服系统对快速性和稳定性有很高的要求，同时其减速机构又有明显的非线性，故本文拟对输入、输出角度换算后的电压误差信号的绝对值进行分段，采用分段式PID控制来获得良好的控制品质。考虑到积分环节在系统短时间内的输出产生很大的偏差时，会使PID运算的积分积累很大，造成系统较大的超调，甚至引起系统大幅振荡，导致系统不稳定，所以本文在研究控制算法时，仅选取了比例和微分2个控制参数。

由于该伺服系统在某些小位置误差范围内，对系统的控制品质有特殊要求，且该伺服系统减速机构有一定的死区因素，故本文拟将控制参数分为五段，以期在小角度误差范围内利用不同的控制率来获得更加优良的控制品质。依据不同的角度差对应的误差信号，确定控制参数的区间分界点为5、40、100和250。当误差信号的绝对值小于5时，系统处于减速机构的死区范围内，将控制参数同时设置为零，控制量输出为零；根据伺服系统在小角度位置差范围对性能的特殊要求，在中间的3个区间段内设置不同的控制参数；当误差大于250时，系统输出与控制目标之间的偏差角度，需要系统拥有较快的响应速度，故去除微分环节，调节比例环节系数，使系统控制量输出达到饱和，偏差快速减小。各区间比例微分系数的计算公式如下：

(3)

其中，OFFSET为附加偏置量，CON为控制系数。

将以上控制算法写入S函数并置于仿真模型中，完成系统仿真建模。系统仿真模型如图3所示。

图3 某伺服系统仿真模型Fig.3 Servo system simulation model

在分段式PID控制中，如何确定每个区间段内的PID控制参数，使控制系统的性能满足设计要求，是伺服控制系统设计过程中的难点。传统的参数设计在很大程度上依靠专家经验进行人工试凑，且调节过程需要反复迭代、修改，不仅设计周期长，而且参数仍存在优化空间，无法达到最优化设计。鉴于此，在伺服系统设计中，迫切需要一种简单可行的设计方法来满足设计需要。

3 伺服系统控制参数的多目标优化设计

本文采用智能优化算法——NSGA-Ⅱ，选择各区间的控制参数为优化变量，以伺服控制系统的性能指标作为优化目标，寻找伺服系统控制参数的最优解。

3.1NSGA-Ⅱ算法

印度研究人员Srinivas和Deb在20世纪90年代提出的NSGA算法，是用非支配排序思想将多目标优化问题简化为一个适应度函数的方式[6]。在此基础上，Deb于2002年提出了改进型的NSGA-Ⅱ。相比以往的多目标遗传优化算法，它降低了计算的复杂度，引入了拥挤度和拥挤度比较算子。在进化过程中将父代种群与由其得到的子代种群相结合，保证父代中的优秀个体不会丢失，以提高种群水平[7]。

NSGA-Ⅱ具有一定的并行性，是对种群当中的个体分别进行操作，排除了种群个体不同初值所带来的影响，有效地降低了算法对变量初值的敏感性。此外，在对种群执行进化操作的同时，可以方便地添加约束条件，避免出现不可行解，提高了算法的求解效率。图4给出了NSGA-Ⅱ的流程[8]。

图4 NSGA-Ⅱ流程Fig.4 Process of NSGA-Ⅱ

3.2 目标函数

衡量控制系统的指标有稳定性、准确性和快速性三个方面。系统的快速性通过上升时间来反映，上升时间越短，控制目标实现的就越快，系统就有越好的品质。但如果片面地追求系统的动态特性，得到的参数可能会使控制信号过大，导致系统在固有饱和特性的作用下变得不稳定。因此，在选择目标函数时，应综合考虑上升时间和误差等约束条件。同时，由于适配函数与目标函数相关，所以可以直接将目标函数作为适配函数进行参数寻优。

3.2.1ITAE准则

ITAE准则是一种广泛应用于控制系统参数优化设计中的目标函数，它是时间与误差绝对值乘积的积分，其表达式为

(4)

以误差e(t)组成的泛函作为一种“损失函数”，则式(4)表示控制系统在转换状态时，以最小代价的损失实现控制目的。所以，当式(4)取极小值时，则说明控制系统具有ITAE最优控制。时间t对误差e(t)的加权作用，在对控制系统动态性能影响最大的中间段，逐渐增强，抑制误差增大，促进系统快速收敛。因此，选用ITAE准则构成目标函数，最优控制具有平稳、快速的过渡过程[9]。

3.2.2 相移量最小化

对于伺服系统来说，由于系统结构、外作用形式以及元器件的饱和特性、运动部件的死区、间隙、摩擦特性等非线性因素影响，某一时刻系统输出总会滞后于输入一定的时间，即相位滞后。系统的相移反映系统输出跟随输入的特性，相移小，则系统响应就快。所以，通常采用相移量来衡量系统响应的实时性和快速性。这里采用FFT法测得的某一频率fin的输入的相移量S作为评估伺服系统性能的第二优化指标[10]。

设v(t)为频率为fin的控制信号，y(t)为伺服系统的输出，系统控制(运算)周期为fsam。按周期采样后，v(t)信号变为vn，y(t)变为yn，采样点长度为N，Ncom为FFT序列中输入信号频率分量的下标，J为幅值比。

V=fft(vn，N)

(5)

Y=fft(yn，N)

(6)

(7)

(8)

(9)

3.3 多目标仿真优化

在模型的输入端设置MultiportSwitch模块，可以实现在相同控制参数情况下，系统对不同输入信号进行仿真，并通过Scope观察系统响应。

3.3.1 伺服控制系统的目标函数与约束

根据伺服控制系统的性能指标要求，选择多目标优化的目标函数如表1所示。

表1 不同输入条件下的目标函数Tab.1 Objective functions of different conditions

考虑到工程实现的实际，在以上目标函数的基础上，增加一个约束，限制控制参数只能为整数。

3.3.2 伺服系统控制参数优化变量

将系统的比例微分环节系数设为偏移量与控制系数同误差绝对值乘积的和，根据分段区间及系统饱和输出时的控制量，可得13个设计变量及其求解空间如表2所示。由表2可知，各设计变量的求解空间很大，完全不需要依赖于专家经验。

表2 伺服系统优化变量Tab.2 Optimized variables of servo system

3.3.3 优化结果

将仿真模型导入多目标优化设计平台modeFRONTIER中，并选择多目标智能优化算法NSGA-Ⅱ进行运算。对所得优化结果分别按照ITAE准则以及最小相移值的指标进行排序，最后综合考虑选择下面一组数据作为系统的最优解[11]。

表3 控制参数最优解Tab.3 Optimal solutions of control parameters

4 结果仿真分析与实验验证

4.1 寻优目标条件下的仿真分析

仿真1：向系统输入端施加15°的阶跃信号，系统仿真曲线如图5所示。由图5可以看出，与由专家依据经验反复调试后设置的控制参数系统仿真曲线相比，经参数优化后系统的响应时间得到了提高，稳态误差也有相应改善(从0.1°减小到0.08°)，超调量从2%上升到2.3%，调节时间缩短了0.0061s。

图5 仿真1结果图Fig.5 Result of the 1st simulation

仿真2：输入频率为10Hz、幅值为2°的正弦信号，系统的响应曲线如图6所示。对比两组参数的响应曲线，相移由原来的15.08°减小到优化后的13.52°，幅值比由原来的1.048下降到1.034，系统性能与专家依据经验反复调试得出的参数控制性能相当，并略有改善。

图6 仿真2结果图Fig.6 Result of the 2nd simulation

仿真3：输入频率为20Hz、幅值为1°的正弦信号，系统的响应曲线如图7所示。同经验参数相比，优化后响应曲线的相移由35.427°下降到29.36°，幅值比由1.162缩小到1.134，性能指标有所改善。

图7 仿真3结果图Fig.7 Result of the 3rd simulation

4.2 不同输入条件下的仿真验证

仿真4：输入幅值分别为4和10的两个连续矩形波，系统仿真图形如图8所示。系统对幅值为4°的阶跃信号响应的超调量为2.9%，调节时间为0.0453s；对10°阶跃信号，系统的超调量为2%，调节时间为0.042s，系统的稳态误差约为0.18°，具有良好的跟随特性。

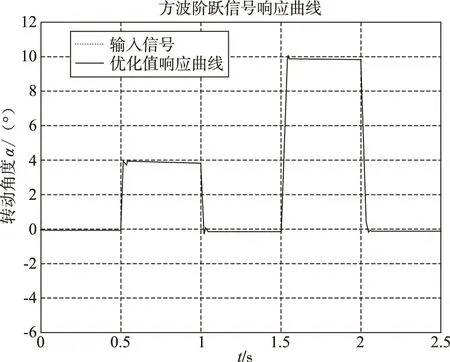
图8 仿真4结果图Fig.8 Result of the 4th simulation

仿真5：输入频率为5Hz、幅值为3°的正弦曲线，仿真曲线跟随良好，相位滞后输入信号7.84°，幅值比约为0.988，说明系统在低频输入情况下控制效果良好，仿真结果如图9所示。

图9 仿真5结果图Fig.9 Result of the 5th simulation

仿真验证结果表明，本文寻优指标下所得到的控制参数对其他不同的输入信号也能获得良好的控制品质。

4.3 实验验证

将本文设计的控制参数与原利用经验设计的参数分别写入该型伺服系统的控制器，并利用实验设备向伺服系统输入频率为10Hz、幅值为4°的低频正弦控制信号和频率为20Hz、幅值为1°的高频正弦控制信号，记录测试结果，测试结果对比如图10所示。

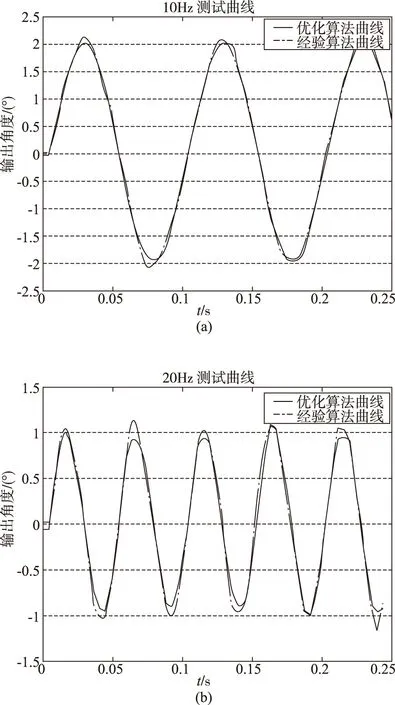
图10 伺服系统性能实验测试结果Fig.10 Performance test results of servo system

图10中，利用本文所提出的控制参数优化设计方法所得到的控制参数，其系统响应曲线与根据经验试凑所得参数的响应曲线相比，跟踪平稳，输出平滑，波形畸变小，在相移这项关键性能指标上也相差无几，同时，在响应波峰与波谷输出角速度接近零的小位置误差处，本文设计的控制参数可以获得更好的控制精度，幅值也更加接近输入信号。实物测试结果证明，本文的仿真模型与仿真结果拥有较高的可信度。

5 总结

本文将NSGA-Ⅱ多目标优化遗传算法应用于某伺服系统控制参数的优化设计中，并对得到的控制参数进行仿真分析和实验验证。结果表明，仿真结果真实可信，同时，采用该设计方法进行控制参数优化设计，方法简单可行，操作性强，大大缩短了研制周期，有效地节约了研发成本。

[1] 李广文，贾秋玲，刘小雄，等.基于进化策略的飞行控制系统优化[J].飞行力学，2009，27(5)：33-36.

[2] 刘家学，吕继兴.基于进化策略的飞行器纵向控制率设计[J].控制工程，2009，S3.

[3] 毕可军，章卫国，刘宝宁，等.飞机飞行控制多目标优化研究[J].计算机仿真，2012，29(7)：80-83.

[4] 聂瑞，章卫国，李广文，等.基于改进的多目标进化算法的飞行控制系统优化[J].计算机应用研究，2011，28(5)：1703-1706.

[5] 白俊杰，张坤，崔彦勇.飞机飞行控制系统参数多目标优化设计研究[J].航空计算技术，2014，44(2)：91-94.

[6] Srinivas N，Kalyanmoy Deb.Multi-objective optimization using non-dominated sorting in genetic algorithms[J].Evolutionary Computation，1994，2(3)：221-248.

[7] Kalyanmoy Deb，Amrit Pratap，Sameer Agarwal，et al.A fast and elitist multi-objective genetic algorithm：NSGA-Ⅱ[J].Evolutionary Computation，IEEE Transactions on，2002，6(2)：182-197.

[8] 李学斌.基于多目标遗传算法和多属性决策的船舶柴油机转速PID控制器参数优化[J].海军工程大学学报，2009，21(3)：61-65.

[9] 黄勇，肖鲁，阎杰，等.基于ITAE最优控制的电动伺服加载系统控制器设计[J].弹箭与制导学报，2005(2)：506-508.

[10] 路艳洁，席志红，王姜铂.FFT法与数字相关法在相位测量上的比较[J].信息技术，2007(12)：105-108.

[11] 涂环，陈辉.基于多目标遗传算法的汽轮机转速PI控制器参数优化[J].武汉理工大学学报，2014，36(2)：67-71.

The Multi-objective Optimization Design of Control Parameters in Servo System Based on NSGA-Ⅱ

WU Fei，DUAN Li-hua，ZHANG Kun-feng

(China Airborne Missile Academy，Henan Luoyang 471000，China)

A multi-objective optimization design method of servo system control parameters based on fast and elitist Non-dominated Sorting Genetic Algorithm(NSGA-Ⅱ)was proposed to solve the problem of making the design cycle longer and the cost higher，by using the sectional PID control strategy.After servo system simulation model had been established，the unknown control parameters were selected as optimization variables，and three optimal performance indexes of the servo control system were chosen as the optimization goal.The optimal solution was obtained and used in the simulation and physical experiment.The results show that the control parameters based on proposed design method are able to satisfy the requirements of performance of servo control system，greatly shorten the design cycle and save design cost effectively.

Sectional PID control strategy；Servo system；NSGA-Ⅱ；Multi-objective optimization design

2014 - 12 - 18；

2015 - 01 - 12。

航空科学基金(2014ZC12004)

武飞(1987 - )，男，硕士，主要研究领域为伺服系统控制算法设计。

E-mail：roger_fei@163.com>

TP391.9

A

2095-8110(2015)05-0014-08