金融危机前后中信行业指数联动效应及其社团结构比较

谢邦昌，游　涛

(1. 中央财经大学 统计与数学学院， 北京 100081；

2. 台湾辅仁大学 统计资讯学系， 台湾 台北 24205)

金融危机前后中信行业指数联动效应及其社团结构比较

谢邦昌1,2，游涛1

(1. 中央财经大学 统计与数学学院， 北京 100081；

2. 台湾辅仁大学 统计资讯学系， 台湾 台北 24205)

摘要:文章采用平面最大过滤图和InfoMap算法研究中信行业指数网络在金融危机前、中、后三个阶段的联动效应及其社团结构。研究结果表明，三个阶段的指数网络都存在小世界性质，且危机期间的网络联动效应最强；社团结构在危机期间有相互融合的整体趋势即网络变得更加紧密；社团中核心节点存在局部影响优势，某些边缘节点间存在局部强联动效应。

关键词:中信行业指数；平面最大过滤图；社团结构；联动效应

一、 引言

本质上来说，自然界中多数大规模数据集都可以用复杂网络模型进行描述，比如互联网、食物链网络、蛋白质互动网络、学者合作网络、社交网络等[1]。Watts等(1998)[2]441针对上述网络研究发现复杂网络的小世界性质，Barabási等(1999)[3]则发现了复杂网络的无标度性质。这两大特性的发现不仅打破了把复杂网络假设成随机网络的传统认识，同时也使得复杂网络理论在各学科的研究中得到广泛应用。Mantegna(1999)[4]首次应用复杂网络理论研究股票市场，以构成标普指数的500只股票为节点，收益率相关性为连边构建了标普500最小生成树网络(MST)得出其联动效应和层次结构。

此后越来越多的学者开始关注这一领域的研究。从国外文献来看，Micciche(2003)[5]对比了美国股票市场收益率和波动率的MST网络,发现前者动态稳定性强于后者。Gilmore等(2008)[6]构建欧盟21个股票市场指数的复杂网络，使用MST研究了网络内各指数之间的联动机制，发现法国股票市场处于欧盟的核心位置。Eom等(2009)[7]通过对比股票MST和随机矩阵MST，发现最大特征值在股票网络的形成动态过程中起到决定性作用。Ulusoy等(2012)[8]研究了英国40个最大上市企业股票的复杂网络，得出其亚超度量空间上的层次聚类结构和联动特征。Kantar等(2012)[9]研究金融危机对土耳其股票网络的影响，结论表明该网络的联动效应未显著变化，同时危机之后汽车板块在整体网络中的影响力显著提升。Wilinski等(2013)[10]在对法兰克福交易所股票网络的研究中发现中等规模企业在经济危机时期成为MST网络的核心节点。Shirokikh(2013)[11]发现美国股市网络拓扑结构的参数在近十年呈现非单调变化。Ouyang(2014)[12]针对中国四大交易所整体联动性进行研究，发现香港和台湾以及2000年后的上海和深圳股市之间呈现杠杆效应。

从国内文献来看，曾志坚等(2009)[13]利用Johansen协整和Granger因果模型研究金融危机下中国内地证券市场与世界证券市场的联动效应，发现金融危机后内地证券市场对香港与德国市场的影响显著。黄飞雪等(2010)[14]利用MST网络发现全球51个主要市场指数的聚类结构和联动性在金融危机后更加紧密，同时指出复杂网络方法克服了传统VAR、GARCH等计量方法存在的参数指标多样化和数据假设条件苛刻等问题。马源源等(2011)[15]分析了上交所股票网络的富人俱乐部特征，发现Hub节点集对整个网络的风向标作用，以此诊断出股市中的故障性现象。黄玮强等(2013)[16]利用MST方法揭示了股票间信息溢出规律，发现市场因素显著增强了股票信息溢出能力以及此能力的尖峰厚右尾分布性质。

2008年金融危机演变历程的特点是系统风险在各个机构间的关联网络中逐渐形成、积累并迅速扩散至整个经济体，再通过世界金融市场的关联网络进行扩散引起全球金融危机。因此以整体金融网络的结构性质及动态规律为关注焦点的宏观审慎监管政策已经成为各国金融监管体系改革的方向。对于股票市场的传统研究大多采用高斯分布框架下的计量经济学模型，研究少数几个指标序列并通常假定时间序列的正态和平稳性，未能从个体互动的角度揭示整体市场的动态规律，同时正态性的假定认为危机事件是异常小概率事件。本文采用复杂网络的研究方法从个体互动的原始数据出发，研究股票市场的整体动态规律，符合宏观审慎政策的思想，同时克服了需要对数据先验假定的缺陷。近年来越来越多的文献着眼于金融复杂网络，但都是基于宏观层面(以各国市场指数为节点)和微观层面(以单只股票为节点)的探索，很难揭示我国股市中行业板块之间的互动结构和联动效应及其拓扑统计性质。从研究方法来看大多采用MST和阀值过滤法来得到网络模型的邻接矩阵，用层次树来描述其中的聚类结构。MST不允许图形回环和派系结构的存在从而丢失重要信息且因其拓扑结构过于简单导致社团结构挖掘算法无法实现，而阀值过滤法存在阀值选取缺乏客观标准的问题，同时层次树聚类未能客观体现社团数量且可视化程度低。

针对以上文献的不足，本文利用平面最大过滤图算法构建对中信行业指数为节点的复杂网络，用InfoMap算法挖掘该网络的社团结构，以此作为本文研究的起点。Tumminello等(2005)[17]10422提出的平面最大过滤图(PMFG)不仅包括MST的全部信息且放宽了过滤算法的约束条件从而包含更丰富的拓扑结构，并通过纽交所300只股票的实证研究证明了PMFG的优越性。Pozzi等(2013)[18]基于PMFG网络提出节点的边缘测度，并发现美股网络边缘节点组成的资产组合收益率显著高于市场指数。基于信息编码理论的社团结构探测算法InfoMap已被大量实证结果证明为准确率最高的算法之一[19]。因此本文利用中信行业指数2006年6月16日至2014年7月9日的历史数据，并以2008年9月15日和2011年7月21日为分界点，分别构建三个阶段以各行业指数为节点的PMFG网络，利用InfoMap算法探测该网络的社团结构，克服以上文献中网络拓扑结构过于简单，社团结构无法探测的缺陷。通过对比金融危机前、中、后三阶段复杂网络及其社团结构的区别可以揭示各行业指数之间联动效应及社团结构的变化规律，并发现网络拓扑结构以及核心节点影响力的变化，从而能够有效揭示股票市场中观结构的互动关系，弥补原有文献只关注个股和市场指数的不足。对核心节点实施重点监督更有利于市场维稳，取代对所有节点或简单以节点市值大小进行监督的管理方式。同时行业指数之间的联动效应和社团结构对于风险管理和投资组合来说也具有重要意义。

二、 研究方法

(一) 平面最大过滤图的构建

1．完全连接网络。假设网络中包含N个行业指数，则行业指数i的对数收益率为：

ri(t)=lnPi(t)-lnPi(t-Δt)

(1)

其中i=1,2,…,N，Pi(t)为第i个行业指数时点t的收盘价，Δt为时间间隔(本文中是一天)，这样得到每个行业指数的收益率序列。根据此收益率序列计算任意两个行业指数i和j在观测区间内的价格波动相关系数，即：

(2)

其中ri和rj分别为行业指数i和j的收益率序列，E(·)为数学期望。由各行业指数之间的两两相关系数ρij可以得到一个完全连接网络G(N,W)，N代表节点(行业指数)集合，W代表节点连边权重集合(价格波动相关性)，且本文采用相似权即权重越大代表相似度越高距离越短，则任意一对节点i和j的连边权重wij=ρij[17]10423。完全连接网络包含噪声信息，需要用平面最大过滤图算法过滤掉冗余的边得到最终的行业指数网络。平面最大过滤图算法可以看作广义最小生成树，因此依次介绍这两种算法。

2.最小生成树(MST)。MST通过(N-1)条边将N个节点连在一起且不允许回环和派系结构，具体算法如下：(1)初始MST是含有N个节点但没有任何边的网络，并对完全连接网络G(N,W)中的边按照权重降序排列；(2)选择序列中第一条边加入MST；(3)顺序从序列中选出下一条边加入MST并判断其是否与已存在的边形成回环，如果有则舍弃；(4)重复步骤(3)直到MST中边的数量达到(N-1)。

3.平面最大过滤图(PMFG)。PMFG算法建立在MST基础上，区别如下：(1)放松了MST中新加入边不能与已有边形成回环的限制，仅要求新边加入后仍然是可平面图，即所有边可以不交叉地画在一个平面上；(2)节点和边的数量分别为N和E的可平面图满足E≤3(N-2)，因此边的数量不是(N-1)，而是3(N-2)。

(二) InfoMap社团挖掘算法

Rosvall等(2008)[20]提出社团结构可以被认为是复杂网络邻接矩阵中信息的压缩表示，并对网络中随机游走现象产生显著影响，即随机游走一旦进入某社团，将以更高的概率在该社团内部游走。基于这一思想InfoMap算法把网络随机游走看作信息流，使得社团结构划分问题转化成信息流路径编码问题，并通过最小化平均编码长度的期望值来得到最佳网络社团的划分，该算法的目标函数定义：

(3)

上式中，L(Z)表示随机游走运动于社团内部和社团之间时所留下路径的平均编码长度的期望值，该目标值越小则对应的某种结构划分越接近网络社团结构的真实划分。q代表随机游走游离某社团进入另一个社团的概率。H(Zinter)表示在给定某划分Z的条件下，随机游走在各社团之间运动概率的熵。pi表示随机游走存在于某社团Zi内部的概率。H(Zi)表示随机游走在社团Zi内部节点之间运动概率的熵。

三、 实证分析

(一) 样本数据

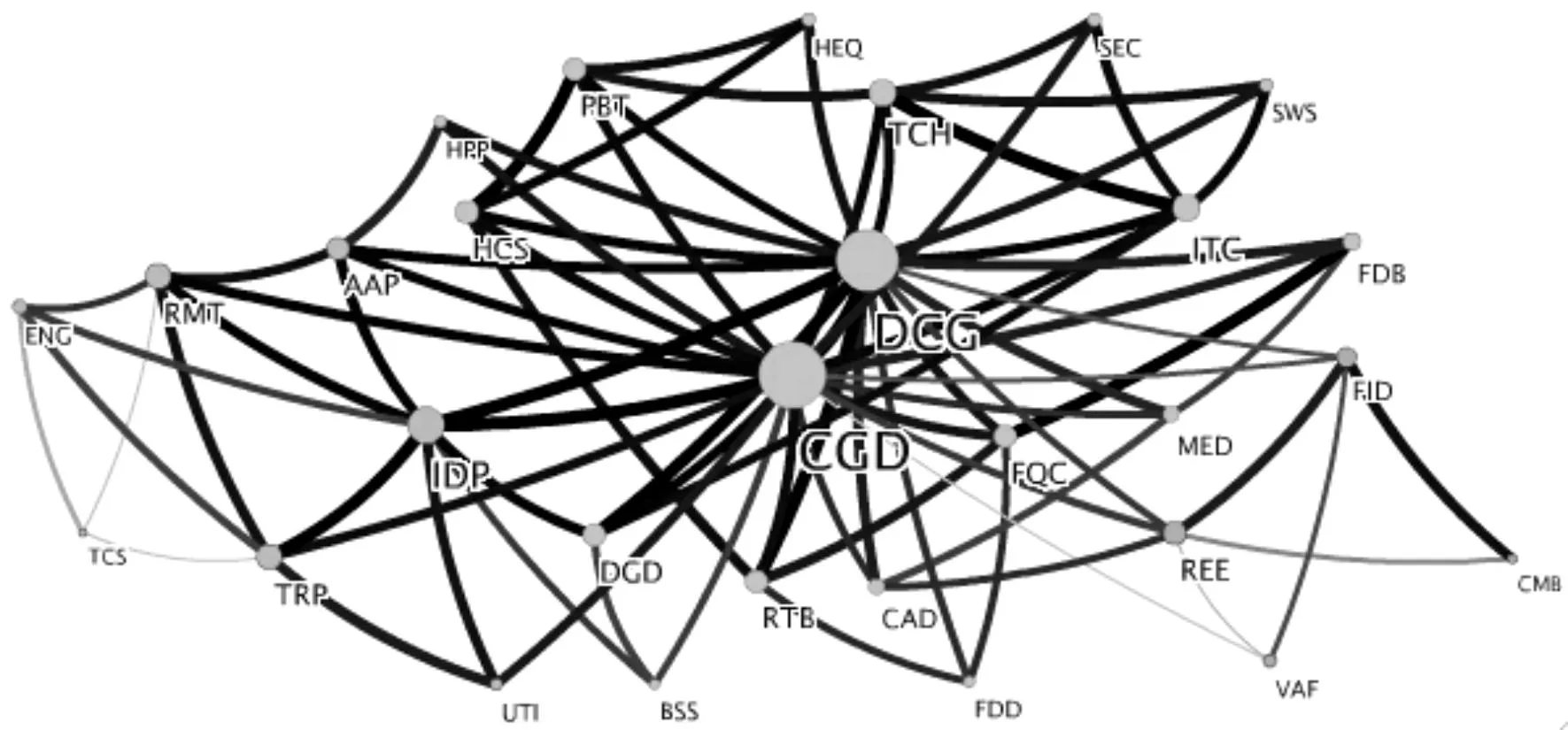
图1　金融危机前中信行业指数的PMFG图

本文采用的数据是2006年6月16日至2014年7月9日的中信行业指数收盘价时间序列日数据，每个序列有1960个观测值，数据来自中信行业指数官方网站。2008年9月15日，美国最大投资银行之一的雷曼兄弟宣布破产，美林银行被美国银行收购，导致了世界金融市场的巨变。直到2011年7月21日欧盟向希腊提供1090亿欧元的贷款援助，这段时间是金融危机和欧债危机对世界经济冲击最严重的时期。因此选择2008年9月15日和2011年7月21日为临界点，以这3段时间的样本数据来对比危机前、中、后行业指数复杂网络的变化对了解行业板块之间的联动效应和社团结构稳定性具有重要意义。本文数据处理使用R3.10复杂网络图形制作使用Matlab2014。

(二) 中信行业指数PMFG网络拓扑结构分析

图1、图2、图3分别为中信行业指数3个阶段的PMFG图，其中节点的大小代表节点在整个网络中的影响力，连边的粗细代表两个节点之间联动性的强度，各行业指数英文缩写见表1。

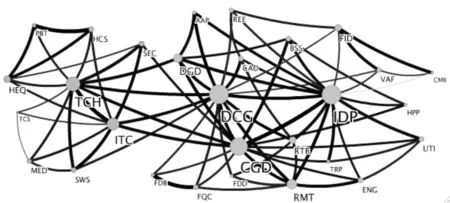
图2　金融危机中中信行业指数的PMFG图

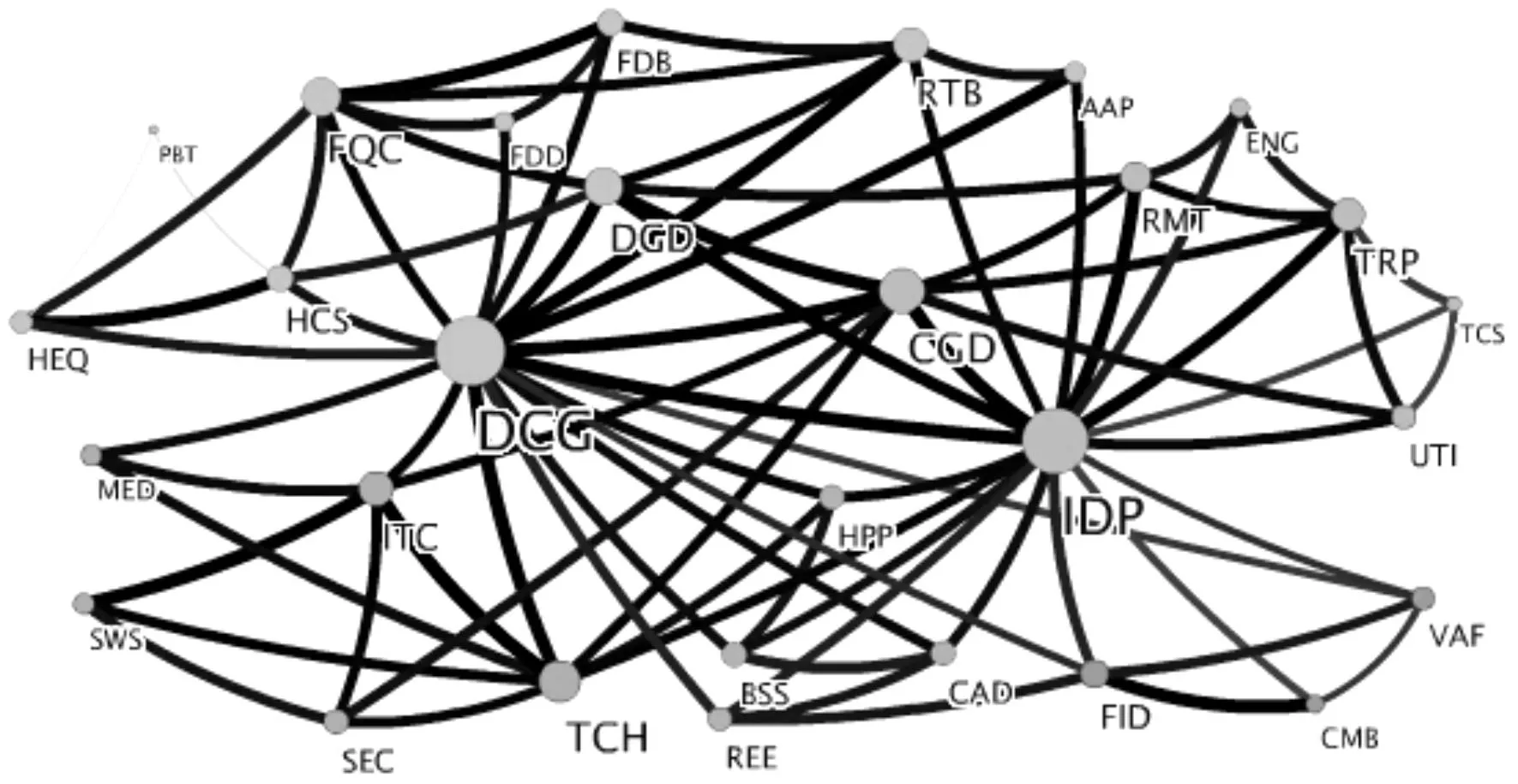
图3　金融危机后中信行业指数的PMFG图

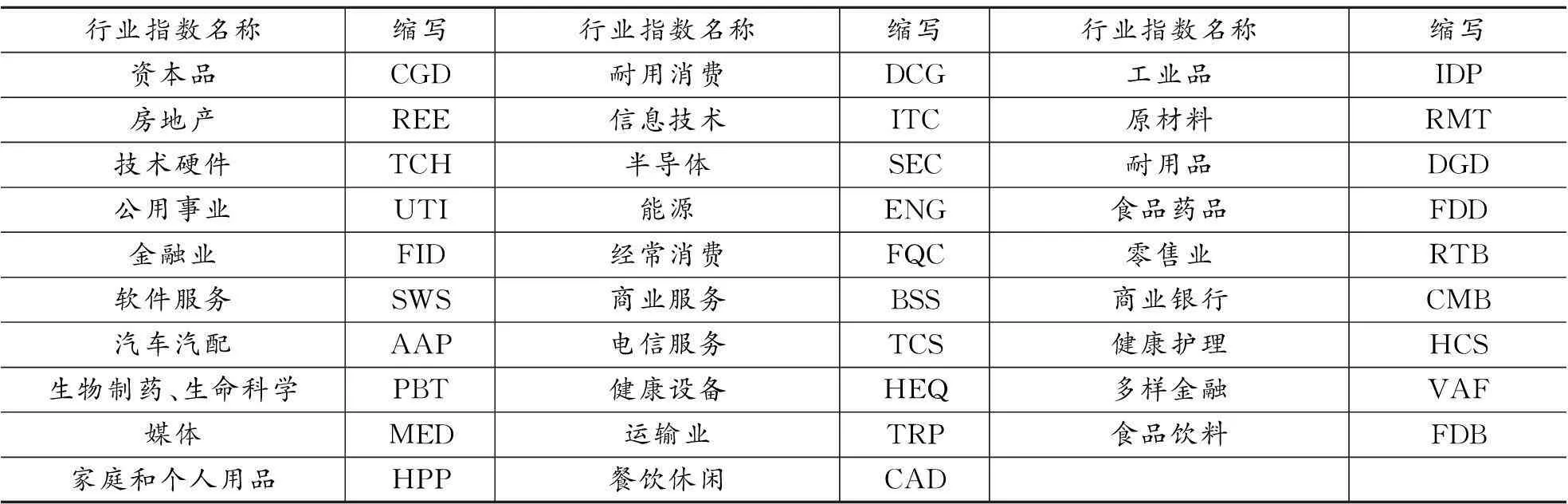
行业指数名称缩写行业指数名称缩写行业指数名称缩写资本品CGD耐用消费DCG工业品IDP房地产REE信息技术ITC原材料RMT技术硬件TCH半导体SEC耐用品DGD公用事业UTI能源ENG食品药品FDD金融业FID经常消费FQC零售业RTB软件服务SWS商业服务BSS商业银行CMB汽车汽配AAP电信服务TCS健康护理HCS生物制药、生命科学PBT健康设备HEQ多样金融VAF媒体MED运输业TRP食品饮料FDB家庭和个人用品HPP餐饮休闲CAD

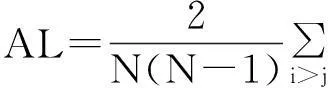
由表2可知三个阶段的核心节点的前三位始终为资本品、耐用消费、工业品，且节点影响力在危机中的分布倾向于更加均匀。表明我国近十年股票市场中影响力最大的仍然是传统生产型行业，与我国以出口和投资为主要经济增长点的国情相符。这与其他国家的研究结果不同，通用电器(GeneralElectirc)是道琼斯工业指数的核心节点[21],德国DAX30指数中德意志银行(DeutscheBank)是核心节点[22]，金融业在伦敦FTSE100指数中有最强影响力[23]，这表明我国作为新兴市场和成熟市场仍有一定距离。同时由于资本品主要是生产中使用的机器设备、钢铁、石化、有色金属等，受宏观经济影响大且有较强周期性，由其度数和介数的下降可以发现资本品的影响力及其联动性在金融危机后显著下降。其中我国钢材2009年上半年的出口量同比下降69.01%，钢材价格从2008年6月最高的161.47点下降到2009年4月的95.56点，整体经济的投资需求下降导致多数钢企亏损。2008年11月稀土金属出口额同比下降了75.1%，与10月的数据相比下降了40.8%*数据来源与中国海关网站，足见其萎缩的幅度和速度，并为资本品行业影响力下降提供了证据。同时技术硬件、信息技术在危机期间取代了房地产、运输业，成为核心节点之一。这代表我国房地产行业的历史性爆发增长在金融危机之后相对趋于平缓，IT类行业逐渐成为新的快速增长领域。在危机后经常消费和耐用品成为核心节点，由图3可知经常消费和医疗保健类行业产生了较强的联动关系，从而使得前两个阶段相对边缘的经常消费行业成为核心节点。

表3　中信行业指数网络平均路径长度及平均聚集系数

值得一提的是金融危机期间工业品度数超过了资本品和技术硬件，但其介数却比后者少，由图2、图5可见工业品所有连边都在D社团内部，只为社团内部各节点的间接联动效应做出贡献。而资本品和技术硬件可以看作是两个社团之间的桥梁节点，为更多的节点提供最短路径，不同社团之间的节点都要通过资本品和技术硬件实现最有效的间接联动。

由表3可知三个阶段平均路径长度分别为2.23、2.15、2.37，与随机网络取值2.4接近，平均聚集系数分别为0.37、0.41、0.36远大于随机网络的0.089。当一个复杂网络与其等规模随机网络具有接近的平均路径长度，且平均聚集系数远大于随机网络，则此网络具有小世界性质[2]442。因此金融危机前、中、后三个阶段的PMFG网络的小世界拓扑性质非常稳健，表明我国股市整体活跃程度高，波动性传导快。金融危机期间相对于其他两个阶段，网络平均聚集系数较大，平均路径长度较小，表明金融危机期间的网络具有更紧密的拓扑结构和联动效应。原因在于大盘指数从2008年1月5500点一直降到2008年11月不足2000点，之后虽然小幅度涨跌，但总体仍然在低位波动。这个时期投资者对于企业利润下降的预期显著强于危机前且风险偏好也明显下降，某行业指数偶然下跌很容易导致投资者抛售其他行业股票，溢出效应导致整体市场下跌的连锁反应，偶然事件的系统性风险被放大。

(三) 行业指数网络社团结构分析

图4、图5、图6为金融危机前后3个阶段的社团结构，通过对比可以发现社团数量在危机中下降，相比前后两个阶段，社团有相互融合的整体趋势，而危机前后社团结构较为分散。同时金融危机期间原有以工业制造类和地产金融为核心的社团B和C融合到了社团A中。主要原因是随着金融危机在世界范围蔓延，我国三大贸易伙伴美国、欧盟、日本的需求骤减导致我国传统型工业制造行业受到极大冲击。金融危机之前金融类(金融业、商业银行、多样金融)和房地产独立成为社团C，并以房地产为核心，代表这段时期房地产业是各大金融机构最主要的服务对象和投资对象，其股票价格波动体现出很强的联动效应。危机期间房地产和金融业受到的严重影响显而易见，因此以收益率相关系数矩阵来构建的复杂网络中，在面对外来冲击时受影响大的节点会产生较强的联动效应，从而融合成一个社团的概率更高。相反IT类和电信类有巨大的内需支撑，2009年上半年软件产业业务收入4270.2亿元同比增长22.7%，增速同比下降7.7%；电信服务业营业收入12240.3亿元同比增长2.3%；电子信息制造业同比下降0.6%*数据来源于工信部网站；医疗服务类亦有巨大的国内刚性需求作支撑。因此这几类行业融合成以IT类为核心的社团E，反应出IT类行业影响力的提升。以上结论与本文拓扑结构分析的结论一致。

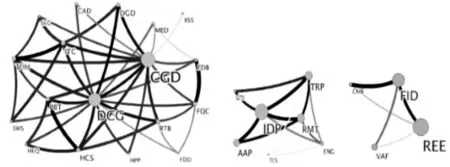
图4　金融危机前PMFG网络社团结构，从左至右命名为社团A、B、C

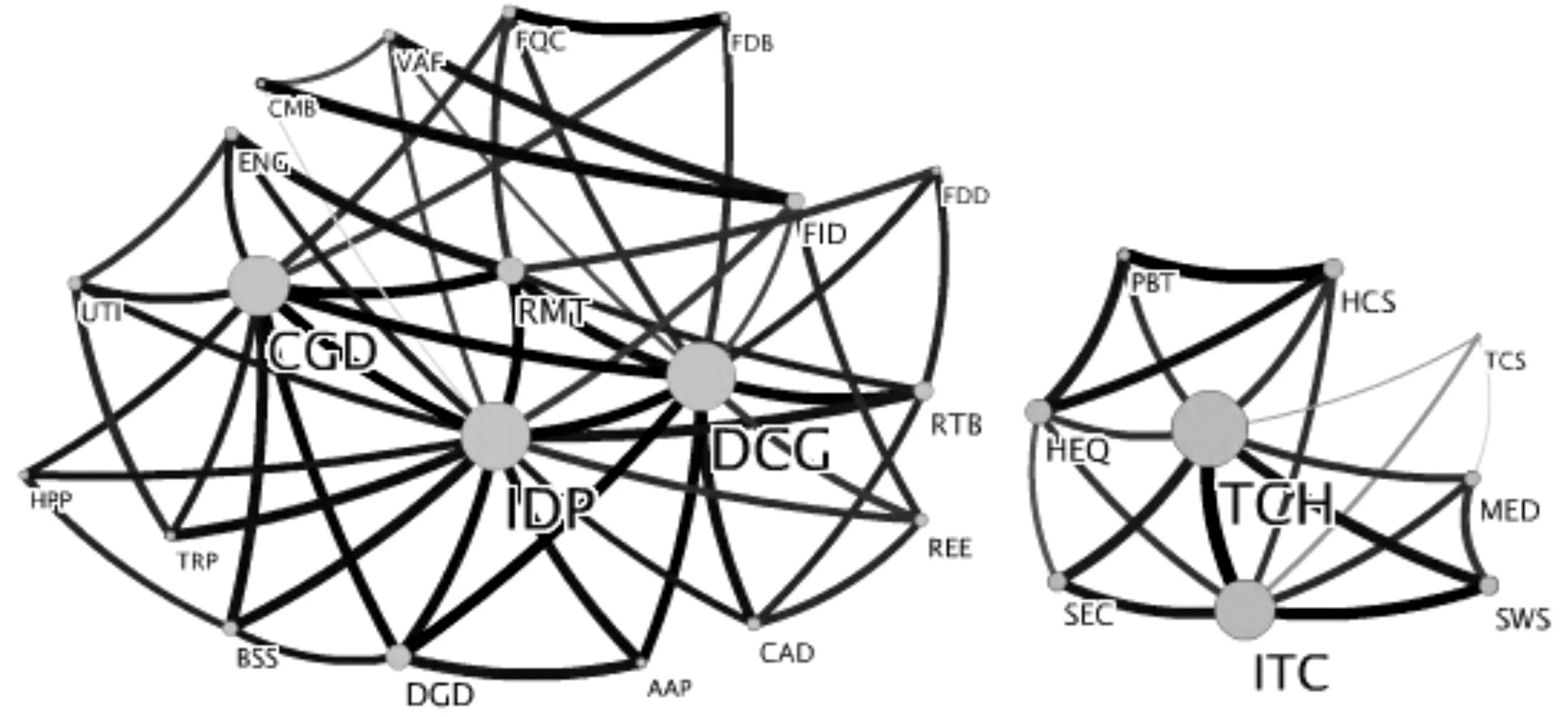
图5　金融危机中PMFG网络社团结构，从左至右命名为社团D、E

图6　金融危机后PMFG网络社团结构，从左至右命名为社团F、G、H、I、J

值得注意的是，由表2可知危机前资本品的度和介数分别为22和182，耐用消费为19和108，因此在整个网络中资本品的影响力更大。但由图4可知在社团A中耐用消费和资本品的度数分别为15和14，且资本品和边缘节点商业服务是弱连接，因此耐用消费取代资本品成为社团核心节点，反应节点的局部影响优势。由图5可知在社团D中工业品相对耐用消费也存在局部影响优势。由此我们可以判断耐用消费和工业品的发展分别对社团A和D中行业的发展具有更大的促进作用，从而为有针对性的产业发展提供了决策依据。另外由图4可见信息技术和技术硬件、食品饮料和经常消费、生物制药、生命科学和健康护理在整个网络中都是边缘节点，但是从连边的宽度来看，他们两两之间却有着很强的局部联动性。图5中健康设备、健康服务、生物制药、生命科学之间也存在强局部联动性。图6中由于社团结构更加细化，此类现象更加明显，反应出整体网络的碎片化趋势。局部强联动效应表明行业受整体宏观经济的影响不大，但是这些行业指数之间的联系非常紧密，当整体股票市场受到巨大外生冲击影响时，这一信息对于降低投资组合风险来说具有重要意义。由以上社团结构的分析我们可以发现在金融危机之前各行业指数的波动状况主要源于各行业自身的发展，从而指数波动具有明显的异质性，社团结构更清晰。金融危机中期各行业指数的波动都受到外生冲击的巨大影响从而指数波动的异质性减弱，指数之间联动性更强导致社团结构清晰度下降。金融危机后经济开始恢复从而使得各指数波动又开始呈现良好的异质性，表明对于中国股市来说整体外生冲击的影响已经逐渐消退。

四、 结论与展望

本文利用PMFG过滤中信行业指数收益率的相关系数矩阵，分别得到金融危机前、中、后的行业指数PMFG图，并用InfoMap算法分别挖掘其内在的社团结构。通过对比研究得出了以下主要结论：

第一，通过对比PMFG和随机网络的平均最短路径和平均聚集系数发现三个阶段中信行业指数网络都具有稳健的小世界性质，危机期间网络节点的联动效应变得更加紧密，风险溢出效应更强。对于监管机构来说，如果发现股票指数下跌，且网络更加紧密就应该警惕未来危机的系统风险；

第二，资本品、耐用消费、工业品在三个阶段的网络中始终都处于核心节点前三位，但资本品影响力下降明显。另外随着IT类等高科技产业在我国经济中起到更重要作用，危机后已取代房地产等行业成为核心节点。

第三，由于金融危机中期各行业指数都受到巨大的外生冲击，导致各行业指数波动异质性减弱，相比危机前后社团结构更加简单。危机后社团结构清晰度提高可以看出中国股市已经逐渐摆脱外生冲击的影响。

第四，耐用消费和工业品在前两个阶段都不是整个网络中最强节点，但在其社团中却有最强联动效应，体现出局部影响优势。同时发现了边缘节点之间的局部强联动效应，提供了对降低投资组合风险的重要信息。

金融危机对全球股市的冲击是巨大的，在宏观审慎政策的思想下监管机构应该更多关注节点互动关联引起的系统风险，从节点在网络中位置和影响力的角度有针对性地关注网络核心节点来实现稳定市场的目标。本文从行业指数层面揭示了股票市场中观结构的互动关系，弥补了原有文献只关注个股和市场指数的不足。研究方法上采用了PMFG和InfoMap算法使得行业指数网络具有更好的拓扑性质，但由于本文在对称邻接矩阵的基础上得到无向网络以此研究行业指数之间的联动效应，金融风险在网络中的传播路径和方向尚不明朗，在今后的研究中可以试图建立非对称邻接矩阵从而得到有向金融网络来观测风险传播的路径和方向。同时金融网络中存在着复杂性和非线性的特点，该领域的研究都是基于皮尔逊相关系数矩阵，此方法只能捕捉到网络中的线性关系，在以后的研究中将尝试采用更加广义的相关测度以求更加接近真实的网络性质。

参考文献:

[1]DOROGOVTSEV S N,MENDES J F F.Evolution of Networks:From Biological Nets to the Internet and WWW[M].Oxford:Oxford University Press,2003:124-128.

[2] WATTS D J,STROGATZ S H.Collective Dynamics of ‘Small World’ Networks[J].Nature,1998,393(6684):440-442.

[4] MANTEGNA R N.Hierarchical Structure in Financial Markets[J].The European Physical Journal B,1999,11(1):193-197.

[6] GILMORE C G,LUCEY B M,BOSCIA M.An Ever-closer Union? Examining the Evolution of Linkages of European Equity Markets via Minimum Spanning Trees[J].Physica A:Statistical Mechanics and Its Applications,2008,387(25):6319-6329.

[7] EOM C,OH G,JUNG W S,et al.Topological Properties of Stock Networks based on Minimal Spanning Tree and Random Matrix Theory in Financial Time Series[J].Physica A:Statistical Mechanics and Its Applications,2009,388(6):900-906.

[8] ULUSOY T,KESKIN M,SHIRVANI A,et al.Complexity of Major UK Companies between 2006 and 2010:Hierarchical Structure[J].Physica A:Statistical Mechanics and Its Applications,2012,391(21):5121-5131.

[9] KANTAR E,KESKIN M,DEVIREN B.Analysis of the Effects of the Global Financial Crisis on the Turkish Economy,Using Hierarchical Methods[J].Physica A:Statistical Mechanics and Its Applications,2012,391(7):2342-2352.

[10] WILINSKI M,SIENKIEWICZ A,GUBIEC T,et al.Structural and Topological Phase Transitions on the German Stock Exchange[J].Physica A:Statistical Mechanics and Its Applications,2013,392(23):5963-5973.

[11] SHIROKIKH O,PASTUKHOV G,BOGINSKI V,et al.Computational Study of the US Stock Market Evolution:A Rank Correlation-based Network Model[J].Computational Management Science,2013,10(2/3):81-103.

[12] OUYANG F Y,ZHENG B,JIANG X F.Spatial and Temporal Structures of Four Financial Markets in Greater China[J].Physica A:Statistical Mechanics and Its Applications,2014,402(1):236-244.

[13] 曾志坚,徐迪,谢赤.金融危机影响下证券市场联动效应研究[J].管理评论,2009,21(2):33-39.

[14] 黄飞雪,谷静,李延喜,等.金融危机前后的金融主要股指联动与动态稳定性比较[J].系统工程理论与实践,2010,30(10):1729-1740.

[15] 马源源,庄新田,李凌轩.基于复杂网络的上海证券交易所富人俱乐部特性研究[J].东北大学学报,2011,32(3):447-451.

[16] 黄玮强,庄新田,姚爽.复杂网络视角下的我国股票之间信息溢出研究[J].运筹与管理，2013,22(5):177-208.

[17] TUMMINELLO M,ASTE T,MATTEO T D,et al.A Tool for Filtering Information in Complex Systems[J].Proceedings of the National Academy of Sciences of the United States of America,2005,102(30):10421-10426.

[18] POZZI F,MATTEO T D,ASTE T.Spread of Risk across Financial Markets:Better to Invest in the Peripheries[J].Scientific Report,2013,106(7):1656-1665.

[19] LANCICHINETTI A,FORTUNATO S.Community Detection Algorithms:A Comparative Analysis[J].Physical Review E,2009,80(5):56117-561126.

[20] ROSVALL M,BERGSTROM C T.Maps of Random Walks on Complex Networks reveal Community Structure [J].Proceedings of the National Academy of Sciences of the United States of America,2008,105(4):1118-1123.

[21] BRIDA J G,RISSO W A.Multidimensional Minimal Spanning Tree:The Dow Jones Case [J].Physica A:Statistical Mechanics and Its Applications,2008,387(21):5205-5210.

[22] BRIDA J G,RISSO W A.Hierarchical Structure of the German Stock Market [J].Expert Systems with Applications,2010,37(5):3846-3852.

[23] COELHO R,HUTZLER S,REPETOWICZ P,et al.Sector Analysis for a FTSE Portfolio of Stocks[J].Physica A:Statistical Mechanics and Its Applications,2007,373(1):615-626.

(责任编辑孙敬水)

Linkage Effect and Community Structure of CITIC Industry Indices

before and after the Financial Crisis

XIE Bang-chang1,2, YOU Tao1

(1.SchoolofStatisticsandMathematics,CentralUniversityofFinanceandEconomics,Beijing100081,China;

2.DepartmentofStatistics&InformationScience,FujenCatholicUniversity,Taipei24205,China)

Abstract:This paper aims to study the linkage effect and community structure of CITIC industry indices network before, during and after the financial crisis through PMFG and InfoMap algorithm. This paper shows that, small world network character exists in all three periods; the linkage effect has been enhanced during the crisis; community structure has a tendency to merge during the crisis, i.e., more compact; in the community core nodes have local influence advantage, and some marginal nodes show local strong linkage effect.

Key words:CITIC industry indices; PMFG; community structure; linkage effect

中图分类号:F830.91

文献标识码:A

文章编号:1000-2154(2015)01-0080-08

作者简介:谢邦昌，男，教授，博士生导师，博士，主要从事数据挖掘研究；游涛，男，博士研究生，主要从事数据挖掘研究。

基金项目:国家社会科学基金重大项目“大数据与统计学理论的发展研究”(13&ZD148)；国家统计局重大项目“大数据现象、理论及处理技术的发展和创新研究”(2013LZ53)

收稿日期:2014-08-13