零控脱靶量有限时间收敛制导律*

雷虎民，张 旭，董飞垚，李 炯

(1.空军工程大学防空反导学院，陕西西安710051;2.中国人民解放军95437部队，四川彭山620864)

近年来，随着全球空间竞争的日趋激烈，高速机动飞行器的研究受到各国的普遍重视并得到了相当程度的发展，目前，一些高超声速飞行器已经投入军事应用，给各国导弹防御系统带来了严峻的挑战。

在新的拦截情形下，由于弹目相对速度很大，末制导拦截时间又很短，这就对拦截导弹的精确制导技术研究提出了特别的要求［1-3］。文献［1］研究了使视线角速率有限时间收敛的多种高精度制导方法，以满足新一代导弹实现“趋零脱靶量”精确制导能力的要求，取得了良好的制导效果;文献［2］基于Lyapunov稳定性理论分别设计了导弹俯仰平面和偏航平面的视线角速率有限时间收敛制导律，该制导律既能保证系统有限时间稳定，又能够保证其有限时间收敛;文献［3］基于新型自适应非奇异Terminal滑模控制方法，设计了一种部分制导与控制一体化有限时间收敛控制算法，可保证滑模面在有限时间内收敛到零。同时，为了使导弹能够更好地适应新型拦截的实际需要，考虑导弹自动驾驶仪动态特性的制导律也得到了广泛的研究［1，4-10］。文献［4-5］分别考虑导弹自动驾驶仪一阶和二阶动态特性，设计了变结构制导律，但不能使导弹的视线角速率在有限时间内收敛到零;文献［6］运用非线性反步设计法，设计了考虑自动驾驶仪动态特性的终端角度约束滑模导引律，并能够保证导弹的有限时间收敛特性;文献［7］基于有限时间稳定性理论，设计了考虑导弹自动驾驶仪动态特性的有限时间收敛制导律，具有较强的鲁棒性;文献［8-9］通过引入低通滤波器，运用动态面控制方法，设计了考虑导弹自动驾驶仪二阶动态特性的制导律;文献［10］为改善BTT导弹的捕获区性能，设计了考虑导弹自动驾驶仪动态特性的最优制导律，仿真实验证明了其有效性和实用性。文献［11］根据平行接近法原理推导了一种动能拦截器零控脱靶量制导律，具有较高的制导精度;文献［12］设计了基于零控脱靶量的大气层外超远程拦截制导律;但是这两种制导律只能使零控脱靶量在拦截结束时刻收敛到零，不能使零控脱靶量在有限时间内收敛到零。

1 零控脱靶量三维制导模型推导

零控脱靶量的具体表达式有多种形式，对零控脱靶量的定义如下:从当前时刻开始，导弹的制导指令为零，目标按照当前的机动状态继续飞行，最终获得的弹目之间的最小距离。导弹-目标三维相对运动学关系如图1所示。

图1 导弹-目标三维相对运动学关系Fig.1 Three-dimensional relative motion geometry of missile and target

图1中:M为导弹，T为目标，r为弹目相对距离;oxi yi zi为惯性坐标系，oxL yL zL为视线坐标系;θT和ψT为目标的弹道倾角和弹道偏角;θM和ψM为导弹的弹道倾角和弹道偏角;θL和ψL为视线倾角和视线偏角。由图1所示的弹目三维相对运动学关系，可得如下弹目运动方程:

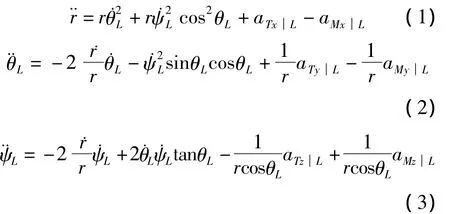
由于重点对导弹拦截目标的末制导段进行研究，可假定导弹中制导结束后，导弹-目标初始对准良好，且整个飞行过程中弹目视线角变化不大［13］。因此，选择以导弹-目标初始视线坐标系oxL0yL0zL0为基准，将三维非线性弹目拦截几何关系解耦为俯仰平面和偏航平面进行单独研究。首先对俯仰平面内的弹-目拦截问题进行研究，如图2所示。

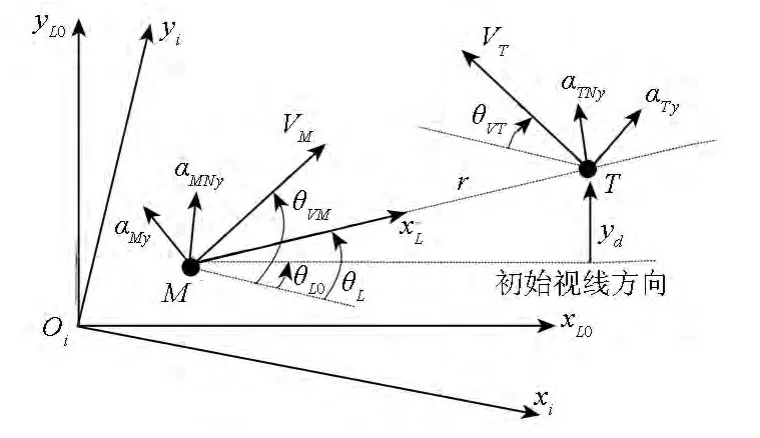
图2 俯仰平面内的弹目相对几何关系Fig.2 Relative motion geometry of missile and target in pitch plane

令ψL=180°，˙ψL=0，则式(1)和(2)可转化为:

式中，Vr和Vy⊥分别为弹目相对速度沿视线方向和垂直视线方向分量。根据几何关系，其表达式如下所示:

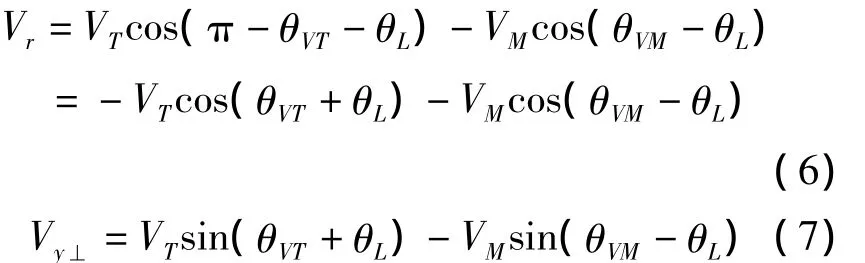
假定在制导末端，导弹和目标的速度大小变化不大，近似认为是常值，则剩余飞行时间tgo可近似由式(8)确定:

令yd，aTNy和aMNy表示r，aT和aM沿初始视线坐标系y方向的分量，则有:

由于在导弹拦截目标的过程中，弹目视线角变化不大［13］，故有:

式中，θL0为弹目初始视线倾角。

为了更加符合实际作战情形，将目标和导弹的动态特性分别视为时间常数为τT和τM的一阶惯性环节，即:

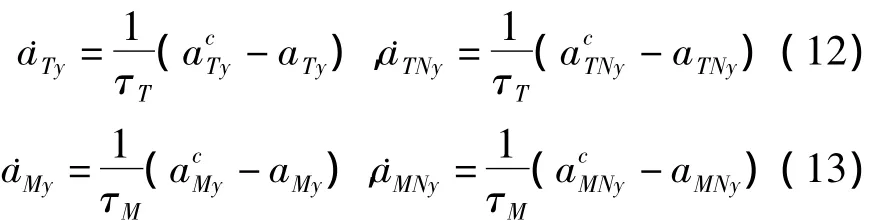
根据零控脱靶量的定义，得俯仰平面内导弹的零控脱靶量yZEM为:

式中，ψ(ξ)=e-ξ+ξ-1，eAGtgo为式(14)关于剩余飞行时间tgo的状态转移矩阵，其表达式为:

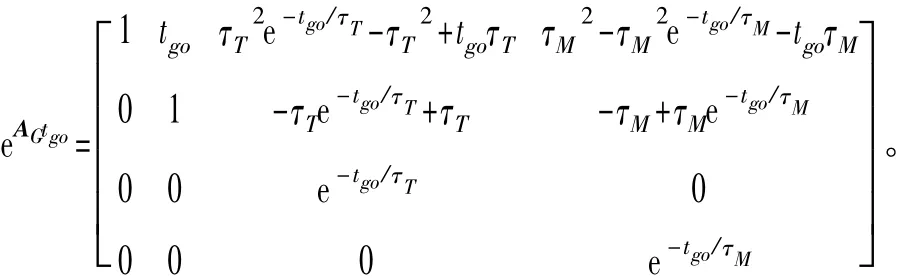
考虑信息的可获取性，对式(15)进行重新整理和化简。根据图2描述的几何关系有:

对式(16)两端求导，可得:

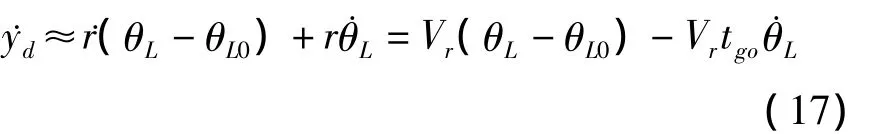
对式(17)两端同时乘以tgo并结合式(16)，可得:

将式(18)代入式(15)，可得:

同理，可得偏航平面的零控脱靶量zZEM为:

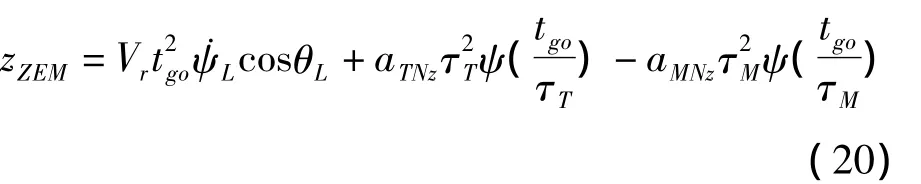
式中，aTNz和aMNz分别表示aT和aM沿初始视线坐标系z方向的分量。

2 零控脱靶量有限时间收敛制导律设计

2.1 制导律设计

根据零控脱靶量的定义，零控脱靶量是当导弹的制导指令为零，目标按照当前的机动状态继续飞行时，所获得的弹目之间的最小距离。因此，若yZEM和zZEM到达并保持到零附近的邻域内，就能够保证导弹-目标的最终脱靶量为零，从而确保导弹准确命中目标。又的相对阶为1，因此可直接选择yZEM为滑模变量:

为了便于后续推导，对式(6)～(8)求导并结合式(2)，可得:

结合式(19)、式(24)和式(25)，可得

证明:由于导弹在拦截目标的过程中，弹目距离不断减小，因此剩余飞行时间也逐渐趋向于零，即

由此，俯仰平面和偏航平面的制导律可设计如下:

式中，μy，μz为大于零的常数，aκy，aκz为自适应因子。

同时，为了克服普通滑模带来的抖振现象，采用如下饱和函数sat(·)代替符号函数sgn(·):

式中，Δ为边界层厚度。

2.2 稳定性分析

选择如下Lyapunov函数:

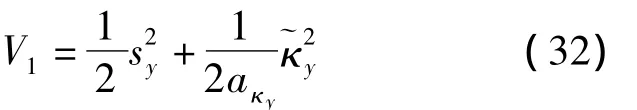
对式(32)两端求导，并结合式(26)，可得:

因此，稳定性得证。同理，可证明式(29)～(30)所示的偏航平面的零控脱靶量有限时间收敛制导律亦能保证系统Lyapunov稳定。

2.3 有限时间收敛特性分析

该制导律设计的目的，就是在考虑导弹自动驾驶仪动态特性的前提下，设计导弹视线角速率有限时间收敛制导律。因此需要对其有限时间收敛特性进行分析，首先给出如下引理［14］。

引理针对自治系统˙x=f(x)，f(0)=0，假设存在连续光滑可微函数V2(x):U→R，使其满足如下条件:

1)V2(x)为正定函数。

2)存在实数c〉0和κ∈(0，1)，以及一个定义在原点的邻域U0∈U，使得下列条件成立:

则上述自治系统是有限时间稳定的;若U=U0=Rn，则该自治系统为全局有限时间稳定。

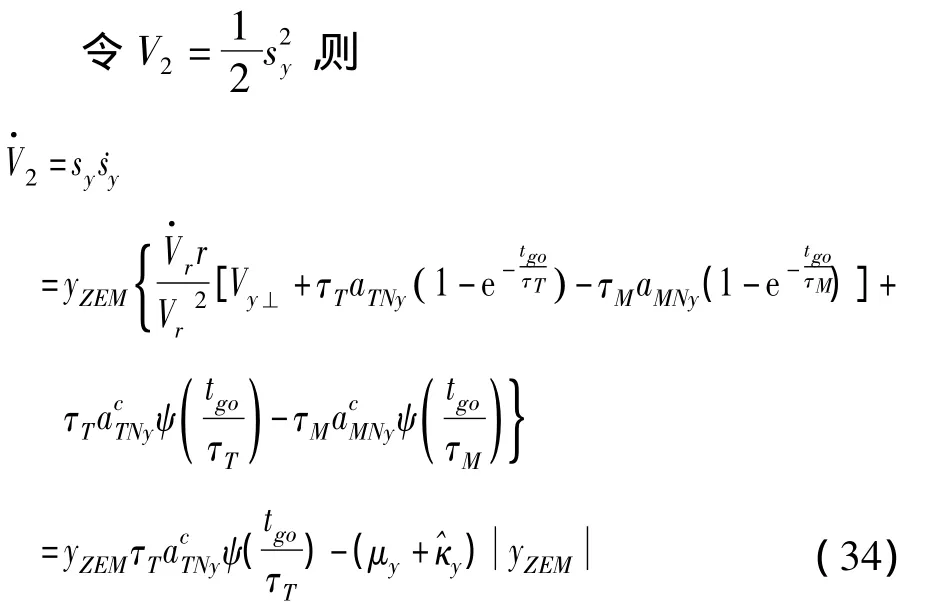
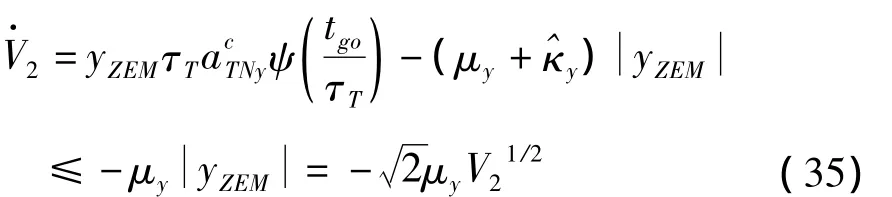
由于采用饱和函数法对制导律的继电特性进行了连续化，因此会对系统的有限时间收敛特性产生一定的影响。如式(36)所示:

3 仿真结果分析

为验证所设计的零控脱靶量有限时间收敛的自适应滑模制导律的有效性，在MATLAB下进行数字仿真，仿真步长为0.01s;但当弹目距离小于300m时，步长为0.01ms。导弹和目标初始参数设置如下:目标初始位置为(26 000m，21 000m，2000m)，速度为1800m/s，初始弹道倾角为170°，初始弹道偏角为0°，目标在俯仰和偏航平面内做正弦型机动，aty=aty0sin(πt/3)，atz=atz0sin(πt/3);由于目标机动加速度延迟时间常数无法测得，故令其机动时间常数为0.01s;导弹初始位置为(0m，19 000m，0m)，速度为1600m/s，初始弹道倾角为4.39°，初始弹道偏角为-4.40°。

此外，仿真中，将所设计的制导律与比例制导律进行对比分析，有效导航比为3.0，为突出考虑自动驾驶仪动态特性的制导律的优势，自动驾驶仪时间常数取较大的0.45s，导弹的最大可用过载为20g;aκy=aκz=0.5，，μy=μz=0.5。为了便于描述，比例导引律用PNG表示，基于零控脱靶量有限时间收敛制导律用FZEM表示，仿真结果如图3～5和表1所示。

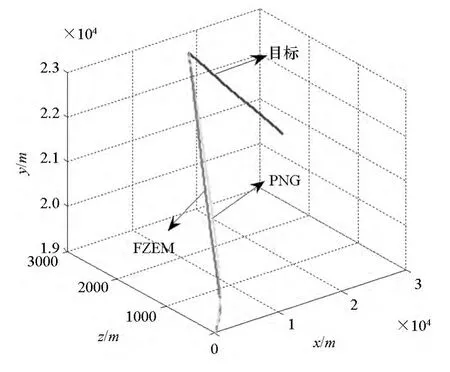
图3 三维弹道轨迹Fig.3 Three-dimensional ballistic trajectories

由图3～4可知，FZEM可保证导弹俯仰平面偏航平面内的零控脱靶量在有限时间内收敛到零，而PN只能保证零控脱靶量在导弹拦截目标结束时刻收敛到零。由图5可知，在拦截初始阶段，FZEM的过载大于PN的过载，此后FZEM的过载均小于PN，这主要是由于FZEM在拦截初始阶段需要较大的过载，使零控脱靶量在有限时间内收敛到零;一旦零控脱靶量达到有限时间收敛，则其过载便会小于PN过载。由表1可知，在目标做不同形式和大小的机动时，FZEM均能够以较小的脱靶量准确命中目标，而PN在aty0较大时，总是出现脱靶。因此，与比例制导律相比，零控脱靶量有限时间收敛制导律具有更高的制导精度，且可使零控脱靶量在有限时间内收敛到零。

图4 零控脱靶量随时间变化曲线Fig.4 Time history of zero-effort miss

图5 导弹过载随时间的变化曲线Fig.5 Time history of missile overload

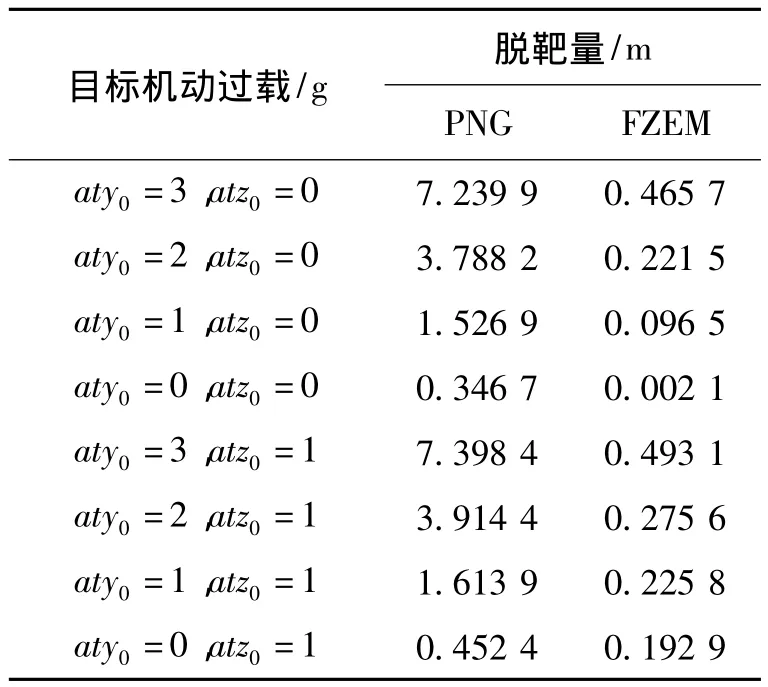
表1 不同制导律拦截性能比较Tab.1 Interception performance comparison between different guidance laws

4 结论

本文针对新型高速机动目标的拦截问题，将弹目三维拦截几何关系解耦到俯仰平面和偏航平面，推导了考虑导弹自动驾驶仪动态特性的新型零控脱靶量制导模型;根据自适应滑模控制理论和有限时间稳定性理论，选取两个平面的零控脱靶量为滑模面，设计了三维零控脱靶量有限时间收敛制导律;选取两种不同的Lyapunov函数，对所设计制导律的稳定性和有限时间收敛进行了详细地分析;通过与比例制导律进行仿真对比分析，表明该制导律具有良好的零控脱靶量有限时间收敛特性，且在目标做不同形式和大小的机动时，均能够有效命中目标，并具有更高的制导精度。

References)

［1］孙胜.有限时间收敛寻的导引律［D］.哈尔滨:哈尔滨工业大学，2010.SUN Sheng.Guidance laws with finite time convergence for homing missiles［D］.Harbin:Harbin Institute of Technology，2010.(in Chinese)

［2］Zhou D，Sun S，Teo K L.Guidance laws with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1838-1846.

［3］Wang X H，Wang J Z.Partial integrated missile guidance and control with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2013，36(5):1399-1409.

［4］佘文学，周军，周凤岐.一种考虑自动驾驶仪动态特性的自适应变结构制导律［J］.宇航学报，2003，24(3):245-249.SHE Wenxue，ZHOU Jun，ZHOU Fengqi.An adaptive variable structure guidance law considering missile's dynamics of autopilot［J］.Journal of Astronautics，2003，24(3):245-249.(in Chinese)

［5］佘文学，周凤岐，周军.考虑自动驾驶仪动态鲁棒自适应变结构制导律［J］.系统工程与电子技术，2003，25(12):1513-1516.SHE Wenxue，ZHOU Fengqi，ZHOU Jun.Robust adaptive variable structure guidance law considering autopilot dynamics［J］.Systems Engineering and Electronics，2003，25(12):1513-1516.(in Chinese)

［6］孙胜，张华明，周荻.考虑自动驾驶仪动特性的终端角度约束滑模导引律［J］.宇航学报，2013，34(1):69-78.SUN Sheng，ZHANG Huaming，ZHOU Di.Sliding mode guidance law with autopilot lag for terminal angle constrained trajectories［J］.Journal of Astronautics，2013，34(1):69-78.(in Chinese)

［7］Sun S，Zhou D，Hou W T.A guidance law with finite time convergence accounting for autopilot lag［J］.Aerospace Science and Technology，2013，25(1):132-137.

［8］曲萍萍，周荻.考虑导弹自动驾驶仪二阶动态特性的三维导引律［J］.航空学报，2011，32(11):2096-2105.QU Pingping，ZHOU Di.Three-dimensional guidance law accounting for second-order dynamics of missile autopilot［J］.Acta Aeronautica et Astronautica Sinica，2011，32(11):2096-2105.(in Chinese)

［9］Qu P P，Zhou D.Observer-based guidance law accounting for second-order dynamics of missile autopilots［J］.Journal of Harbin Institute of Technology，2013，20(1):17-22.

［10］Yeom J H，Hong J W，Yoo S J.Terminal-phase optimal guidance law for BTT missiles considering significant autopilot dynamics［C］//Proceedings of AIAA Guidance，Navigation，and Control Conference，Portland，Oregon，2011.

［11］郑立伟，荆武兴，谷立祥.一种适用于大气层外动能拦截器的末制导律［J］.航空学报，2007，28(4):953-958.ZHENG Liwei，JING Wuxing，GU Lixiang.A terminal guidance law for exoatmospheric kill vehicle［J］.Acta Aeronautica et Astronautica Sinica，2007，28(4):953-958.(in Chinese)

［12］陈峰，肖业伦，陈万春.基于零控脱靶量的大气层外超远程拦截制导［J］.航空学报，2009，30(9):1583-1589.CHEN Feng，XIAO Yelun，CHEN Wanchun.Guidance based on zero effort miss for super-range exoatmospheric intercept［J］.Acta Aeronautica et Astronautica Sinica，2009，30(9):1583-1589.(in Chinese)

［13］李运迁.大气层内拦截弹制导控制及一体化研究［D］.哈尔滨:哈尔滨工业大学，2011.LI Yunqian.Integrated guidance and control for endoatmospheric interceptors［D］.Harbin:Harbin Institute of Technology，2011.(in Chinese)

［14］丁世宏，李世华.有限时间控制问题综述［J］.控制与决策，2011，26(2):161-169.DING Shihong，LI Shihua.A survey for finite-time control problems［J］.Control and Decision，2011，26(2):161-169.(in Chinese)