锥形运动控制的导弹姿态稳定性分析*

段笑菊，孙瑞胜，白宏阳，薛晓中

(1.南京理工大学瞬态物理国家重点实验室，南京210094;2.南京理工大学能源与动力工程学院，南京210094)

锥形运动是导弹以固定攻角绕速度矢量旋转，形成一个以速度矢量为中心的圆锥面的运动现象［1］。它能够使导弹产生等幅的诱导攻角，增加弹体阻力，降低飞行速度。所以，锥形运动控制是实现导弹飞行速度控制的有效途径［2-4］。但是，锥形运动也会产生如附加的马格努斯效应、陀螺效应导致的通道间严重耦合等，严重时甚至造成弹体飞行失稳。美国的奈特霍克探空火箭在试验中就曾很多次出现了发散的锥形运动。

近年来，国内外众多学者纷纷展开锥形运动控制的策略和稳定性研究，提出了多种建模和分析方法。1969年Peterson［5］首先分析了导致锥形运动的可能因素:发射不确定因素、起旋系统的不同轴性、能量耗散、初始扰动、马格努斯力和力矩等。为进一步了解锥形运动产生的原因，1970年Tobak采用风洞试验的方法证明了马格努斯力和力矩是产生极限圆锥运动的主要原因之一。1972年Schiff［6］采用旋转坐标系解稳态欧拉方程，计算了圆锥体圆锥运动中的超音速非黏性的流场。在此基础上，Nicolaides［7］通过理论推导和风洞实验证明了旋转诱导产生的面外力和面外力矩是产生锥形运动的直接原因。此后，很多学者又通过不同的方法针对锥形运动的机理开展了更加深入的研究。赵良玉［8］探讨了圆锥运动稳定性判别与弹道仿真一体化的分析方法，提出通过判断速度最大点的圆锥运动稳定性来评估整个飞行过程中的圆锥运动稳定性态势。李奉昌［9］采用奇点理论与振幅平面方程推导了非对称赤道阻尼力矩作用下产生极限圆锥运动的条件;还有一些学者［10-12］直接利用刚体导弹运动方程结合李雅普诺夫方法及劳斯判据，对锥形运动及其运动发散的条件进行研究和数值仿真，但都没有从陀螺效应的角度直接对锥形运动的生成机理和运动方式进行分析，因此有必要从导弹锥形运动控制的需求出发，研究基于锥形运动控制的稳定性判定方法，为导弹速度控制的方案设计提供依据。

1 导弹速度控制的姿态稳定性分析

锥形运动一般有全攻角和复攻角［13］两种数学描述方法，在国内外现有文献中，采用复攻角方法研究导弹运动及稳定性的成果较多，主要是通过将弹体运动分为长周期运动(质心运动)和短周期运动(姿态运动)［14］，分析弹体的姿态运动特性，并将弹体绕质心的姿态运动近似为攻角运动，这种锥形运动稳定性的研究方法对低空弹道是行之有效的。

在锥形运动控制中，采用如图1所示的控制结构，其中ωn为阻尼回路的穿越频率，nyc，ny分别为飞行控制系统俯仰通道的过载指令和实际过载;Kω，Ka为控制参数，Gp(s)，Gg(s)，Ga(s)分别表示舵机环节、角速率陀螺、加速度计传递函数，均看作放大系数为1的比例环节。锥形运动弹体模型的详细推导过程可参考文献［15］。为分析控制系统对弹体稳定性的影响，将制导控制环节作为弹体攻角方程的一部分，采用李雅普诺夫稳定性判定方法分析弹体的稳定特性。

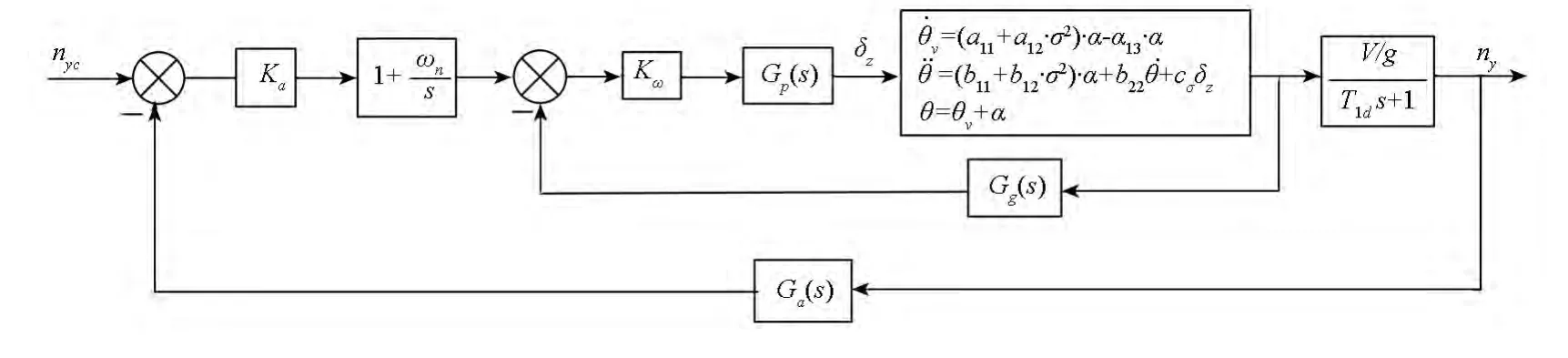
图1 导弹纵向通道控制结构Fig.1 Control structure of the missile longitudinal channel

1.1 控制回路对导弹的影响分析

通常导弹采用轴对称气动布局，因而纵向与侧向通道的控制结构相同，锥形运动控制的控制律为

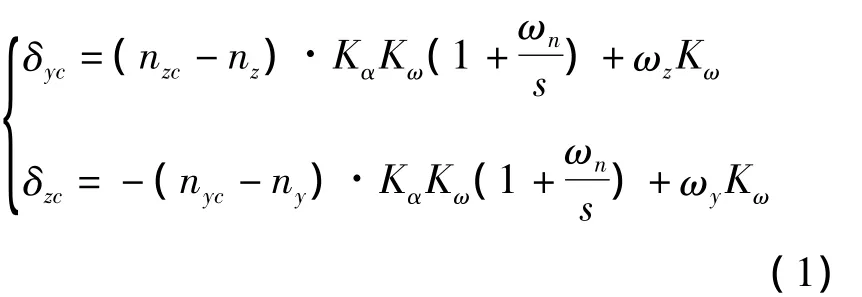
导弹的实际过载可表示为

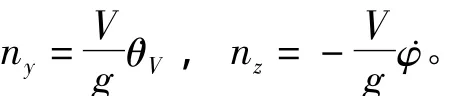
导弹锥形运动控制的导引指令包括两部分，分别为锥形运动指令和比例导引指令，如式(2)所示，其中锥形运动指令在纵向和侧向平面分别采用正弦和余弦的过载指令。

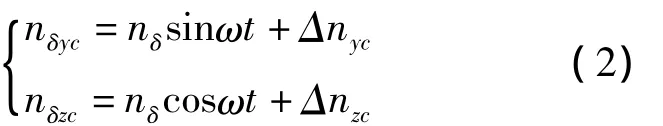
式中，ω为交变角速度，nδ为指令攻角对应的过载指令。将式(2)带入式(1)可得:

令Φ=θV+iφ，下标C表示复平面的控制信息，则δC=δzc+δyc·i，nC=nyc+nzc·i，ωC=ωz+ωy·i。将式(3)合并可得复平面的控制律:

由导弹复平面的姿态关系，文献［15］通过详细的推导得到如下关系:

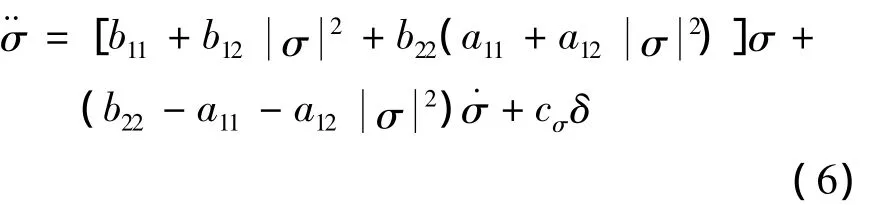
忽略马氏力a13等小量，可得

将式(7)代入式(4)，化简可得

将式(8)带入式(6)，消去δC，可得关于复攻角的二阶非齐次微分方程

控制系统的稳定性是指弹体受到干扰后，长周期和短周期运动幅值均具有收敛趋势，从数学意义讲，就是要求齐次运动方程特征根具有负实部。对于上式所示的非齐次运动方程，其稳定性可以通过齐次微分方程的特征根判定。

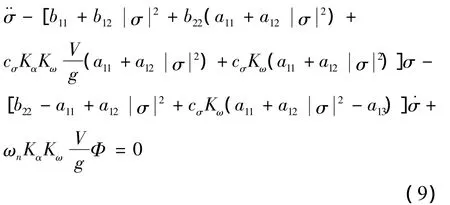
为方便推导，定义

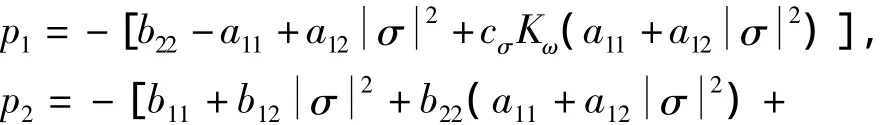
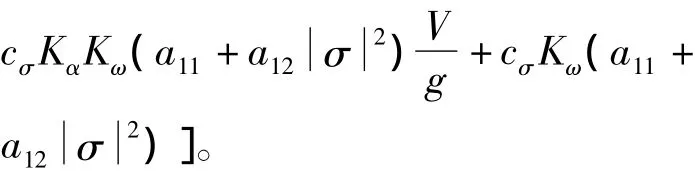
定义x=［Φσ˙σ］T，可得状态方程:

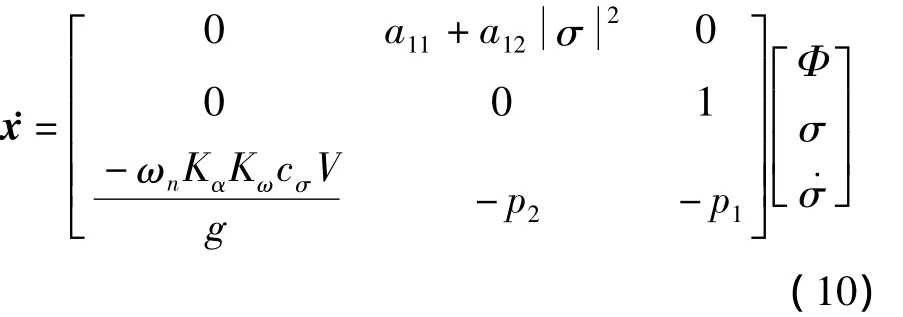
式(10)的特征多项式为

根据数值分析理论［16］，式(12)的所有特征根均在复平面负半轴的充分必要条件为

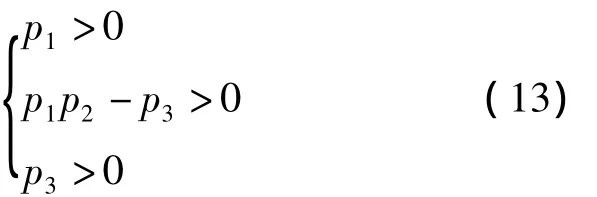
忽略与b22的乘积项，整理可得:

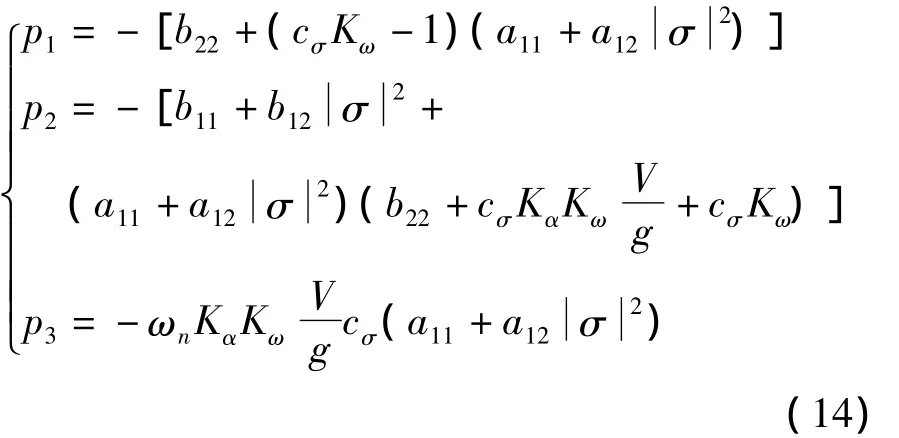
第二种形式可表示为

由于p1p2-p3〉0，因此弹体稳定性条件为

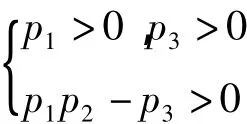
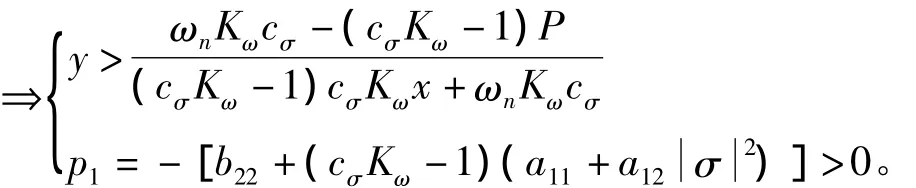
进一步整理可得

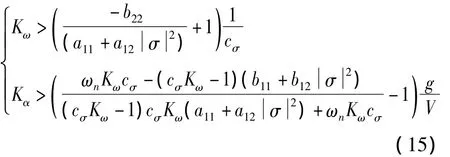
稳定性条件式(15)具有明显的物理意义:即要求做锥形运动时保持弹体复攻角σ所需的控制力矩必须大于复攻角σ产生的气动力不稳定力矩，才能保证导弹受到干扰后依然能够回到初始运动状态。在实际情况中，导弹控制系统不仅要求满足稳定性条件，还必须:①具有一定的稳定裕度，以提高系统抗干扰能力;②补偿系统元件惯性和弹性特性;③具有较好的动态响应特性，即较快的收敛特性和较小的过渡时间和超调量等。

1.2 阻尼回路对导弹的影响分析

根据式(15)推导得到的锥形运动控制稳定性必要条件，采用基于增益调度的自适应控制方法［17］设计飞行控制系统控制回路的控制参数Kα。令Kα保持不变，对比不同阻尼回路控制参数对弹体稳定性的影响。以表1所示的特征点为例研究控制系统性能，根据式(15)所示的稳定性判定方法，若基于锥形运动控制的导弹能够保持稳定，阻尼回路参数Kω必须大于0.12。

表1 导弹某特征点的动力学系数Tab.1 Dynamic coefficients of a feature point

分别选取Kω=0.2和Kω=0.1，绘制特征点控制系统的频域响应曲线，结果如图2、图3所示。

以某一段弹道为例进行锥形运动控制仿真，过载指令仅包含保持锥形运动的控制指令，复攻角的变化曲线如图4、图5所示。

由仿真结果可见，当控制参数Kω满足式(7)的边界条件时，导弹锥形运动能够保持弹体稳定。反之，若控制参数Kω不满足条件，则复攻角呈发散趋势，弹体出现不稳定现象。

图2 Kω=0.2时的频域响应曲线Fig.2 Frequency response curve when Kω=0.2

图3 Kω=0.1时的频域响应曲线Fig.3 Frequency response curve when Kω=0.1

图4 Kω=0.2时的复攻角变化曲线Fig.4 Curve of the complex attack angle when Kω=0.2

2 基于锥形运动控制的弹道仿真

以导弹末制导为例研究锥形运动控制对弹体稳定性的影响。假设末制导时的初速为450m/s，初始位置(0，10km，0)，初始弹道倾角-20°，弹道偏角0°，目标位置(14km，10km，0)。根据式(15)所示的控制系统稳定性判定方法，绘制控制器参数Kα，Kω的关系曲线，建立控制系统的边界条件，如图6所示。当控制器参数位于图中空白区域内时，导弹的复攻角将保持收敛趋势，反之将发生发散现象。

图5 Kω=0.1时的复攻角变化曲线Fig.5 Curve of the complex attack angle when Kω=0.1

图6 控制系统稳定区间Fig.6 Stable range of the control system

如图7所示，导弹攻角始终绕速度矢量旋转，形成了一个以速度矢量为中心的圆锥面，导弹保持锥形运动飞行。

如图9所示，相比于单纯的比例导引，导弹飞行速度大幅降低。仿真结果表明，所设计的控制器能够克服干扰，使姿态角偏差限制在容许范围内，并根据导引指令改变弹体姿态，满足控制系统稳定性的边界条件。

作为对比，降低控制器带宽，设计不满足稳定性的边界条件的控制器，取Kω=0.5，Kα=0.3，仿真结果如图10至图12所示。

图7 复攻角的变化曲线Fig.7 Curve of the change of the complex attack angle

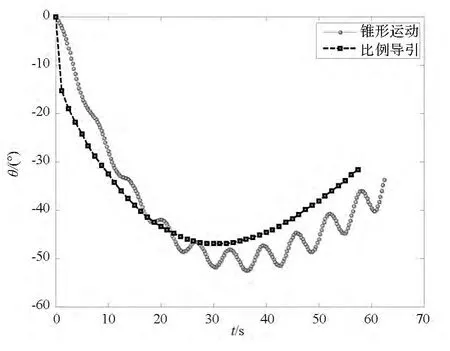
图8 弹道倾角与时间的关系Fig.8 Relation between missile flying-path angle and time

图9 速度与时间的关系Fig.9 Relation between missile velocity and time

阻尼回路的作用是提高系统阻尼，增强弹体的飞行稳定性，使弹体在受到干扰后依然能够恢复到原来的稳定状态，因此必须设计合理的控制参数。当控制回路的控制参数Kα位于不稳定区间时，由图11、图12仿真结果可见，起始10s内，导弹仅采用比例导引，尚未加入锥形运动导引指令时，俯仰、偏航通道的过载跟踪曲线逐渐偏离，特别是锥形运动开始后，导弹虽然能够保持相对稳定，但与设计结果相差甚远，出现明显的控制偏差，导弹在做第八个圆锥运动时，偏航过载指令曲线发散，说明所设计的控制器不能实现导弹锥形运动控制。将图10和图7的复攻角结果仿真对比可以看出，控制参数分别位于稳定与不稳定区域的控制器具有完全不同的控制性能，验证了该导弹稳定性判定方法的可行性。

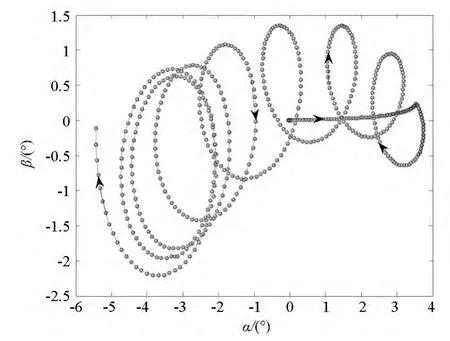
图10 复攻角的变化曲线Fig.10 Curve of the change of the complex attack angle

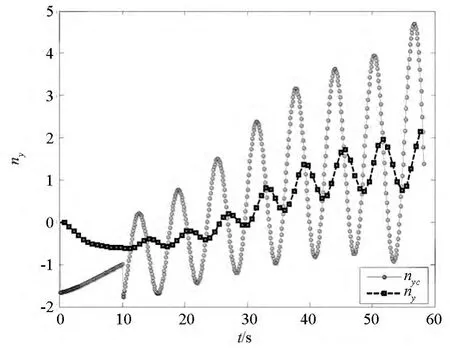
图11 俯仰通道的过载曲线Fig.11 Curve of overload in pitch channel

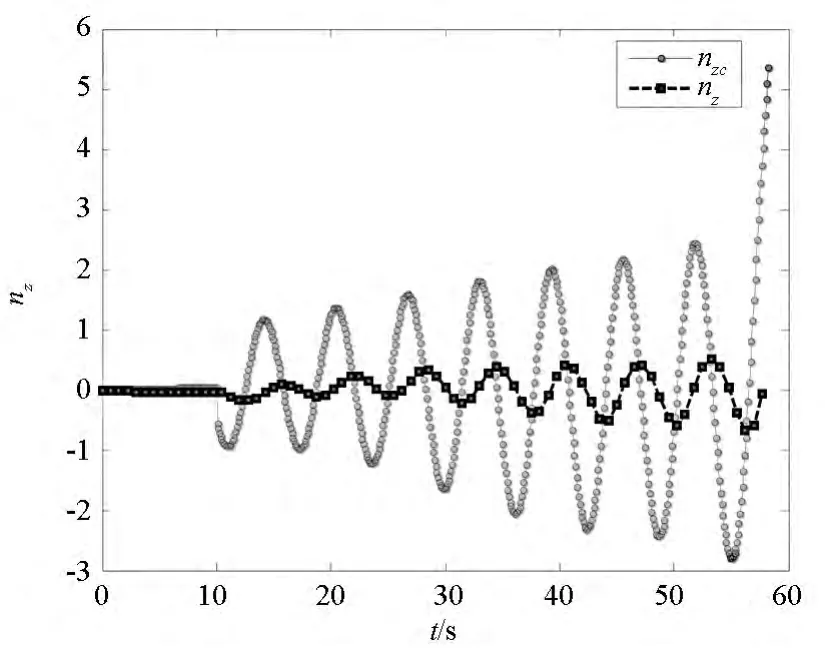
图12 偏航通道的过载曲线Fig.12 Curve of overload in yaw channel

3 结论

本文从锥形运动控制降低导弹飞行速度的需求出发，开展了导弹锥形运动控制的稳定性判定方法研究，建立了导弹锥形运动的控制模型，揭示了控制系统阻尼回路和控制回路对提高导弹锥形运动稳定性的影响规律，提出了一种判定导弹控制系统稳定性的方法。该方法结构简单、思路清晰，能够适应工程实践的应用要求，可以用来判定导弹锥形运动控制时的控制器稳定性，为导弹锥形运动的制导控制系统设计提供了理论基础。

References)

［1］姜玉宪，崔静.导弹摆动式突防策略的有效性［J］.北京航空航天大学学报，2002，28(2):133-136.JIANG Yuxian，CUI jing.Effectiveness of weaving maneuver strategy of a missile［J］.Journal of Beijing University of Aeronautics and Astronautics，2002，28(2):133-136.(in Chinese)

［2］闫晓勇，杨树兴，张成.基于章动运动理论的火箭弹锥形运动稳定性分析［J］.兵工学报，2009，30(10):1291-1296.YAN Xiaoyong，YANG Shuxing，ZHANG Cheng.Analysis of stability for coning motion of rockets based on theory of nutation movement［J］.Acta Armamentarii，2009，30(10):1291-1296.(in Chinese)

［3］Mao X R，Yang S X，Xu Y.Coning motion stability of wrap around fin rockets［J］.Science in China Series E:Technological Sciences，2007，50(3):343-350.

［4］徐浩军，朱建太，曾凡.飞机纵向摆动及飞行安全评估［J］.航空学报，2003，24(3):255-258.XU Haojun，ZHU Jiantai，ZENG Fan.Longitudinal oscillation and flying security evaluation［J］.Chinese Journal of Aeronautics，2003，24(3):255-258.(in Chinese)

［5］Peterson V L，Schiff L B，Tobak M.Aerodynamics of bodies of revolution in coning motion［J］.AIAA Journal，1969，7(1):95-99.

［6］Schiff L B.Nonlinear aerodynamics of bodies in coning motion［J］.AIAA Journal，1972，10(11):1517-1522.

［7］Nicolaides J D，Ingram C W，Clare T A.Investigation of the non-linear flight dynamics of ordnance weapons［J］.Journal of Spacecraft and Rockets，1970，7(10):1241-1243.

［8］赵良玉，杨树兴，焦清介.提高卷弧翼火箭弹圆锥运动渐近稳定性的几个方法［J］.固体火箭技术，2010，33(4):369-372.ZHAO Liangyu，YANG Shuxing，JIAO Qingjie.Several methods for improving asymptotic stability of coning motion of wrap-around-fin rockets［J］.Journal of Solid Rocket Technology，2010，33(4):369-372.(in Chinese)

［9］李臣明，刘怡昕.非对称赤道阻尼力矩对远程火箭弹道的影响［J］.弹道学报，2009，21(2):36-39.LI Chengming，LIU Yixin.Influence of unsymmetrical equatorial damp moment on long-range rockets trajectory［J］.Journal of Ballistics，2009，21(2):36-39.(in Chinese)

［10］Livshits D S，Yaniv S，Karpel M.Dynamic stability and free flight rockets［J］.AIAA-1996-1344-CP.

［11］Liano R.Analysis of control and guidance of rolling missiles with a single plane of control fins［J］.AIAA-2000-3971.

［12］Mao X R，Yang S X，Xu Y.Research on the coning motion of wrap around fin projectiles［J］.Canadian Aeronautics and Space Journals，2006，52(3):119-125.

［13］韩子鹏.弹箭外弹道学［M］.北京:北京理工大学出版社，2008:127-201.HAN Zipeng.Arrow external ballistics［M］.Beijing:Beijing Institute of Technology Press，2008:127-201.(in Chinese)

［14］闫晓勇.旋转弹动态稳定性与控制研究［D］.北京:北京理工大学，2010.YAN Xiaoyong.Rotating cylinder dynamic stability and control research［D］.Beijing:Beijing Institute of Technology，2010.(in Chinese)

［15］Li K Y，Yang S X，Zhao L Y.Stability of spinning missiles with an acceleration autopilot［J］.Journal of Guidance Control and Dynamics，2012，35(3):774-786.

［16］Frank E.On the zeros of polynomials with complex coefficients［J］.Bulletin of the American Mathematical Society，1946，52:144-157

［17］刘鹏云，孙瑞胜，李伟明，等.基于锥形运动的制导火箭速度控制导引律设计［J］.航空学报，2014，35(4):933-941.LIU Pengyun，SUN Ruisheng，LI Weiming，et al.A coning motion-based guidance law for guided rocket with velocity control［J］.Chinese Journal of Aeronautics，2014，35(4):933-941.(in Chinese)