基于关联光子对的双缝量子成像实验

杨　青，夏慧枝，陈　凯

(中国科学技术大学 量子物理和量子信息研究部,安徽 合肥 230027)

基于关联光子对的双缝量子成像实验

杨青，夏慧枝，陈凯

(中国科学技术大学 量子物理和量子信息研究部,安徽 合肥 230027)

摘要：双缝量子成像实验利用参量下转换过程产生的光子之间的关联性，扫描双缝量子成像. 通过采集光子符合计数，绘制扫描位置和光子符合计数关联图，在一维方向重现双缝. 根据实验采集数据和绘图结果计算双缝缝间距.

关键词：鬼像；关联光子对；非局域特性；杨氏双缝干涉

1引言

1993年，巴西科学家通过纠缠光源符合计数成像，使原本由于退相干而消失的杨氏干涉条纹重新呈现. 自此这种具有非局域特性的量子成像的研究便迅速开展开来. 量子成像又称“鬼成像”，不同于常规的直接记录成像方式. 它采用一个单像素点探测器收集透过物体的光，而用另一个单光子探测器在非物空间探测光强分布，通过提取具有关联性质的强度信息完成对物体的非局域成像. 这种有悖于常规思维的成像方式，不仅成像不受光路扰动影响，而且成像的分辨率可以超越衍射极限，也可以对低于奈奎斯特采样率情况扫描成像. 量子成像的这些特点吸引了大量的相关研究，促进了多个科学领域的发展，并且产生了广阔的应用前景[1].

2实验原理

基于“双光子干涉”的量子解释[2]：对于杨氏双缝干涉实验，当传播路径信息不可知时，光子路径信息以概率幅的形式来叠加，从而才出现干涉现象；当试图通过测量来确定路径时，干涉就会消失(费曼路径选择). 基于纠缠源的量子成像是通过符合测量来提取物体的信息，而符合测量手段恰好消除了关联光子对的路径信息(量子橡皮)，即发生干涉现象.

图1为纠缠光子对进行符合测量，当D2探测到光子时，D1探测到的另一光子无法确定传播路径，符合计数是概率幅叠加(干涉)的结果.

图1　双缝干涉

N.Klyshko提出“Advanced wave”理论[3]，该理论提供了唯象解释：以探测器D1作为“点光源”发光，光束传播至参量下转换晶体，把下转换晶体表面看作“平面镜”，光束经该平面镜反射后，传播至扫描平面，最终被探测器接收. 该唯象解释可很好地解释基于纠缠光源的非局域成像.

实验证实非线性晶体的参量下转换过程产生的关联光子之间的时间差很小[4]，几乎在10-12s量级，因此近似认为两关联光子同时产生[5]. 产生的关联光子耦合到光纤中，并通过单光子探测器进行探测. 当光子信号进入单光子探测器并被探测到时，则输出1个电脉冲信号. 累计1 s时间内的电脉冲信号则为单路光子计数. 而参量下转换过程产生的关联光子分别进入到单光子探测器后，若均被探测到，则两探测器同时输出电脉冲信号. 在特定符合门宽内，若同时检测到两路光子的电脉冲信号，则输出1个光子符合信号，见图2. 光子符合计数可有效地检验关联光子对数量.

如图3所示，双缝量子成像实验中，物体双缝放置于无空间分辨能力的物臂上，在参考臂一端利用多模光纤在垂直于双缝方向进行一维扫描. 若光子之间没有关联性，则无论是在物臂还是在参考臂均无法获得双缝的信息. 由于参量下转换过程产生的光子具有关联性，因此在参考臂通过光子符合可重现双缝，可估算出双缝间距.

图2　光子符合

图3　双缝量子成像系统示意图

3实验内容

本架构下的量子成像实验即是利用这对相互关联的光子对符合测量，完成对物体的非局域成像. 实验的具体实现如图4所示，在信号光光路上(物臂)放置成像透镜，物体(如双缝)置于透镜之后，于是透过物体的光子被耦合器收集到固定的点探测器中. 而在闲置光路(参考臂)的某个平面上通过符合计数的方法进行横向扫描探测. 物体和扫描平面到成像透镜的距离分别为z0和z1+z2，透镜焦距f，满足高斯透镜成像公式：

成像放大倍数为(z1+z2)/z0.

图4　双缝量子成像

实验利用参量下转换过程产生的关联光子对，通过成像透镜对双缝进行量子几何成像，如图5所示. 具体光学过程是：405 nm激光泵浦非线性晶体BBO，通过自发参量下转换方式产生偏振方向相互垂直的关联光子对. 关联光子对经过偏振分光棱镜分束，水平偏振方向的光子耦合到多模光纤中，垂直偏振方向的光子经过透镜和双缝后耦合到单模光纤中. 在参考臂上，闲置光子强度分布则被多模光纤横向探测扫描. 两臂的探测结果通过符合计数器对2路光子信号进行符合测量，绘出符合曲线即物体的一维量子几何成像.

图5　双缝量子成像光路图

实验系统中环境光以及泵浦激光对实验结果有很大影响,因此系统中需做好滤波和遮光处理. 在实验系统中，选择在暗室环境下实验，并在光路的各个点设置滤波器件，该滤波器件可滤除99%以上的泵浦光，如此可提高信噪比. 另外，考虑到实验的可观性和有效性，设定数据采集时间为50 s，即每组数据为累计50 s时间内的光子符合计数. 实验曲线如图6所示.

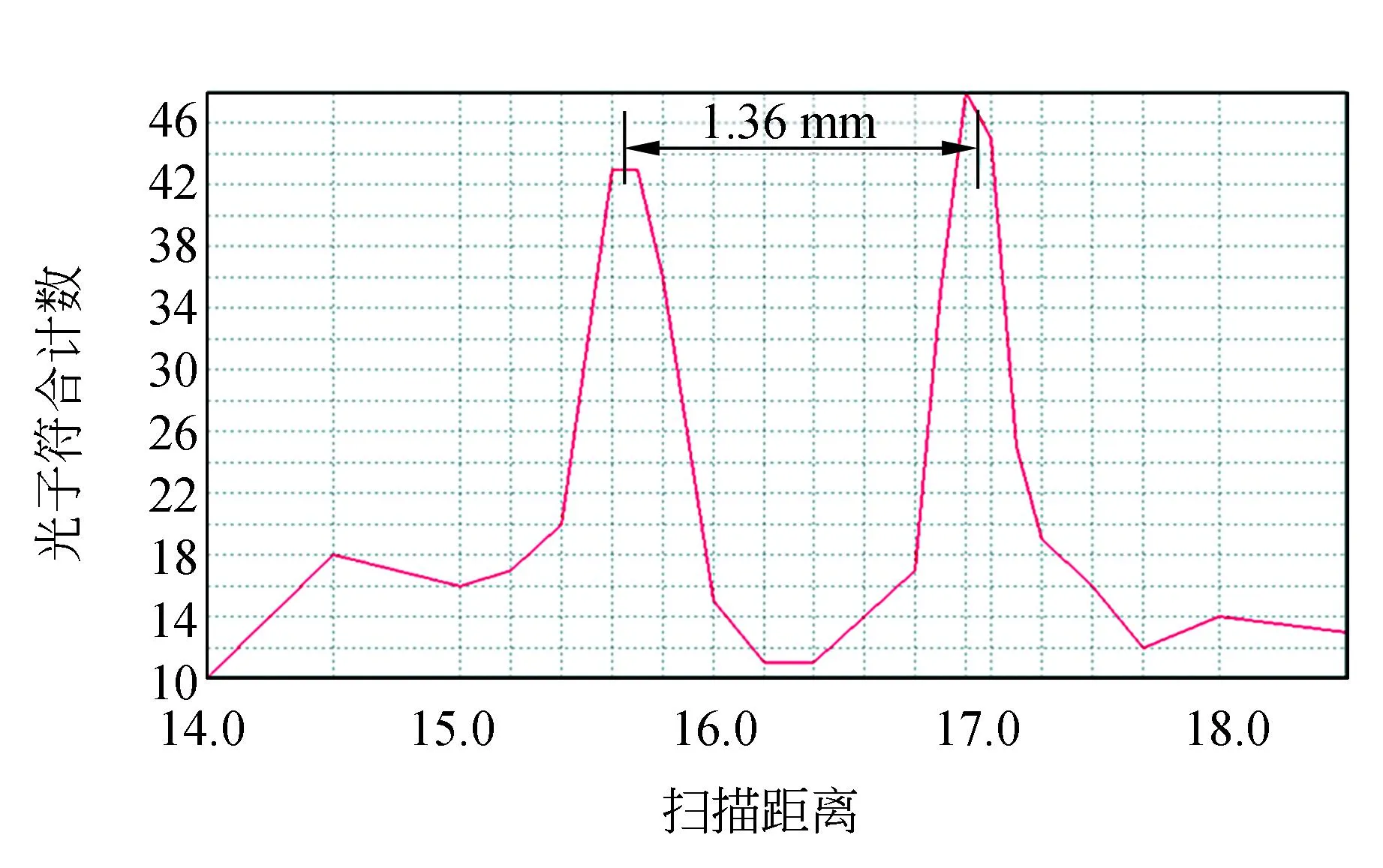
图6　双缝量子成像实验结果图

根据“Advanced wave”唯象理论，成像关系满足高斯公式，成像放大倍数为(z1+z2)/z0. 实验中z0=300 mm，z1=300 mm，z2=300 mm，理论上双缝成像放大2倍，因此一维扫描双缝所得图像的峰值距离为双缝缝间距的2倍. 在本实验架构下实际采集光子符合计数并绘图分析所得图像的双峰间距为(1.36±0.02) mm，成像物体(双缝)的实际间距为0.68 mm. 像距为物距的2倍，与理论分析一致.

4结束语

以成像物体(双缝)为例展示量子成像实验的基本原理以及实验效果. 该实验以扫描双缝一维量子成像为目标，让学生通过本实验了解关联光子对的产生过程，关联光子对的特性，以及利用参量下转换过程产生的关联光子对进行量子成像实验. 实验原理展示清晰，可操作性强.

参考文献：

[1]郑名扬. 基于纠缠光源的量子成像理论与实验研究[D]. 合肥：中国科学技术大学，2013.

[2]Feynman R P， Leighton R B， Sands M. The feynman lectures on physics [M]. Boston:Addison-Wesley,1965.

[3]Klyshko D N. Two-photon Light: Influence of filtration and a new possible EPR experiment [J]. Physics Letters A, 1988,128(3/4):133-137.

[4]Friberg S， Hong C K， Mandel L. Measurement of time delays in the parametric production of photon pairs [J]. Physical Review Letters, 1985,54(18):2011-2013.

[5]Hong C K， Ou Z Y， Mandel L. Measurement of subpicosecond time intervals between two photons by interference [J]. Physical Review Letters, 1987,59(18):2044-2046.

[责任编辑：郭伟]

Double slit quantum imaging experiment based on correlation of photon pairs

YANG Qing， XIA Hui-zhi, CHEN Kai

(Division of Quantum Physics and Quantum Information,

University of Science and Technology of China, Hefei 230027, China)

Abstract:Double slit quantum imaging experiment used the correlation of the photon pairs, which generated by PDC, to scan the double slit quantum imaging. By collecting the photon coincidence number, drawing the correlation picture of scanning position and photon coincidence number, the double slit in one-dimension was reconstructed. The distance of the two slit was calculated in the light of the experiment result.

Key words:ghost imaging; correlated photon pairs; nonlocality; Young double slit interference

中图分类号：O431.2

文献标识码：A

文章编号：1005-4642(2015)03-0037-03

作者简介：杨青(1988-)，女，安徽无为人，中国科学技术大学量子物理和量子信息研究部工程师，硕士，从事量子光学和量子信息方面的研究.

收稿日期：2014-05-30；修改日期：2014-08-19

“第8届全国高等学校物理实验教学研讨会”论文