多区块偏最小二乘回归及在环境-食品重金属迁移中的应用*

蒋红卫张 磊尹 平

多区块偏最小二乘回归及在环境-食品重金属迁移中的应用*

蒋红卫1△张 磊2尹 平1

目的探讨处理复杂数据存在多个变量区块情形的一种统计分析方法：多区块偏最小二乘回归（MBPLSR），并将其用于环境-食品重金属迁移研究之中。方法将重金属镉从环境向大米迁移的影响因素，划分为土壤理化特性与各态镉含量两类，运用MB-PLSR建立环境-大米镉转移模型，并且与传统偏最小二乘回归（PLSR）进行性能比较。结果MB-PLSR较好地利用变量区块的先验信息，使得其无论是在数据拟合、预测性能方面，还是在维度压缩方面，均优于PLSR。结论MB-PLSR适用于具有变量区块的复杂数据建模，具有较好的信息综合和解释能力。

变量区块 成分 重金属 偏最小二乘回归

在许多大型研究中，所需要处理的变量数目达到几十个，甚至成百上千个，通常可以按照某种内涵的相似性，将其划分为多个变量类属（变量区块，variable block）。一般而言，与不同类属的变量相比，相同类属的变量之间往往具有更强的相关性与特定的专业意义，便于信息提取与模型解释［1］。例如，大型流行病学调查中，常将危险因素划分为多个类属（区块），如，人口学指标类、心理行为指标类、生理生化指标类、社会经济指标类等，以期在分析各因素对健康影响的强度基础上，进一步分析各变量类属对健康影响的重要程度。又如，食品重金属污染研究中，常将影响因素划分为土壤重金属指标类、土壤理化指标类、污染排放指标类等，需要明确各因素对重金属从环境向食品迁移的作用。若直接运用传统的统计分析方法，就会导致模型极为庞杂，参数估计不稳定，结果难以分析与解释等问题。目前常用的处理方法主要有两类，一是变量筛选，二是降维。研究表明［2-3］，通过变量筛选，大量解释变量无法按照其在所属区块中的重要性予以纳入或剔除，容易形成错误的统计模型，也无法确定各变量区块的作用，导致对结果虚假的分析与解释。因而，针对具有多变量区块的复杂数据，更偏向于使用降维方法，如多区块主成分分析，多区块偏最小二乘回归（multi-block partial least squares regression，MB-PLSR）等。

作为一种相当高效的第二代统计分析方法，偏最小二乘回归（partial least squares regression，PLSR）集多元线性回归、主成份分析和典则相关分析于一体，同时实现了回归建模、降维与两组变量相关性分析［4］。它采用非线性迭代偏最小二乘算法（nonlinear iterative partial least squares，NIPALS），建立解释潜变量与反应潜变量的回归关系。研究表明［4］，PLS可以有效地降低模型的复杂度，克服了回归分析中多重共线性、高维低样本量等问题，适用于弱理论领域和数据的软建模。由于不同区块的影响因素有着本质差别，因而，必须在一个统一的统计框架下，予以分开处理［5］。针对复杂数据的变量区块特性，Wangen与Kowalski［3，6］提出了多区块偏最小二乘回归。该方法不仅继承了PLSR的优良性质，而且适用于处理变量区块问题，可以更好地解释来自不同区块间变量的作用。因此，本文将在引入变量区块概念的基础上，较系统地研究多区块偏最小二乘回归模型，并用于食品重金属污染实例分析。

基本理论与算法

1.基本思想

假定存在着B＋1个变量区块，包含反应变量区块Y，与B个解释变量区块Xb，b＝1，2，…，B。其中，反应变量区块Y包含一或多个反应变量，解释变量区块Xb包含mb个解释变量，合并解释变量X＝［X1｜X2｜…｜XB］，共含有m＝m1＋m2＋…＋mB个解释变量。所有变量均来自于n个研究个体的观测。MB-PLSR从每个解释变量区块中提取区块成分，再次从区块成分中提取解释变量全局成分，并与反应变量空间成分建立直接的回归关系，从而，间接建立全部解释变量与反应变量的回归关系，其基本思想如图1所示。

图1 多区块数据结构与MB-PLSR思想示意图

2.基本原理

多区块偏最小二乘回归的优化准则如下：

可以证明，反应变量成分u的解为矩阵Y最大特征值所对应的特征向量，区块成分tb（X）是反应变量成分u在解释变量区块Xb的投影。由此可见，MB-PLSR可满足以下两个条件：①尽量提取各变量区块变异信息；②所提取的解释变量区块信息能最大限度地解释反应量的变异信息。

3.基本算法

MB-PLSR在每一步中采用NIPALS，提取各变量区块成分，并获得解释变量全局成分与反应变量成分回归模型的估计。以下是MB-PLSR算法之一：

第一步，将解释变量空间X和反应变量空间Y进行标准化变换，令X0＝X，Y0＝Y。

第二步，指定任意随机数列，作为反应变量Y的成分u0。

第三步，计算解释变量区块Xb第a个成分tab（X）及其权重向量wab（X）。

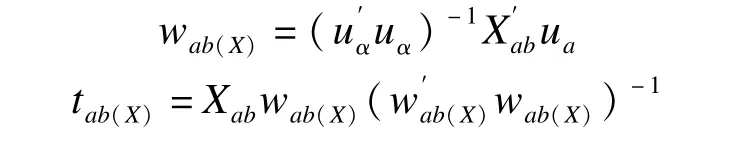
第四步，计算第a个解释变量全局成分及其权重wa（T），以及反应变量Y的成分ua与权重向量qa。

第五步，重复第三、四步，直至第a个全局成分ta（T）收敛。

第六步，计算解释变量X的区块载荷Pb（X）与回归系数B。

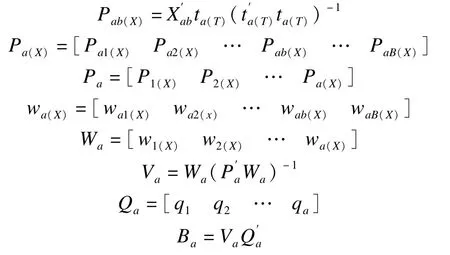
第七步，计算解释变量残差空间Xa＋1与反应变量残差空间Ya＋1。

为了衡量解释变量对反应变量的作用，使用变量投影重要性指标（variable importance of the projection，VIP）来衡量，相关定义见文献［7］。类似于VIP定义，区块投影重要性指标（block importance of the projection，BIP）使用全局成分与反应变量的相关系数平方和来定义［3］，反映各变量区块对反应变量的影响程度与重要性。

本文采用SAS9.3完成多区块偏最小二乘回归模型的统计分析。

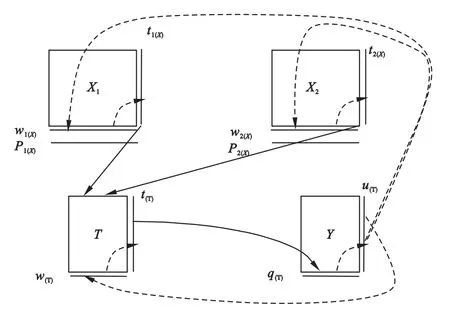
图2 多区块偏最小二乘回归算法图示

实例分析

重金属通过不同形态由环境向食品逐步迁移累积，直接威胁食品安全，造成人群健康水平风险［8］。只有构建合理的环境-食品重金属迁移模型，才能较全面认识重金属迁移的统计规律［9-10］。本实例的食品重金属污染数据来自于2008年湖北省天门市环境与食品污染调查的一部分。具体调查方案是，于晚稻成熟期间，在水稻主产区的岗状平原，采用系统抽样采集52块稻田，获取土壤52份，及其相应的晚稻样品52份。本次调查变量划分三个区块。一是，土壤理化变量区块，含土壤的酸碱度（pH值）、容重（g／cm3）、有机质（%）、交换性酸度（cmol／kg），分别记为x11，x12，x13，x14；二是，各态镉变量区块，包含土壤中总镉（mg／kg）、有效态镉（mg／kg）、碳酸盐态镉（mg／kg）、有机结合态镉（mg／kg），分别记为x21，x22，x23，x24；三是，反应变量大米中镉含量（mg／kg），记为y。其中，各镉含量均取自然对数。现运用MB-PLSR探讨土壤理化特性、各态镉对大米镉含量的影响关系。

对原始数据作标准化变换，采用交叉核实法，确定提取2个全局成分（记为t1（T），t2（T）），同时，在土壤理化变量区块中提取2个区块成分（记为t11（X），t12（X）），在各态镉变量区块中提取2个区块成分（记为t21（X），t22（X）），构建MB-PLSR模型。

各区块成分与其相应的解释变量的关系如下：

其中，t11（X）和t12（X）对土壤理化的解释程度达到70.2%，成分t11（X）主要反映了酸碱度x11与交换性酸度x14的信息，成分t12（X）突出反映了有机质x13的信息；t21（X）和t22（X）对各态镉含量的解释程度达到77.1%，成分t21（X）综合反映了土壤各态镉的信息，成分t22（X）重点反映了有效态镉x22的信息。由此可见，这四个成分分别反映了土壤中酸度水平、有机质水平、总镉水平与易吸收镉水平四类信息。

区块成分与全局成分的关系如下：

其中，t1（T）和t2（T）对反应变量大米镉的解释程度达到65.7%，全局成分t1（T）反映了土壤中酸度水平t11（X）、有机质水平t12（X）、总镉水平t21（X）与易吸收镉水平t22（X）的综合信息，且酸度信息与镉水平呈反向关系，间接表明了原始变量区块分为土壤理化与各态镉水平两区块的合理性；结合全局成分t1（T）和t2（T）可见，土壤中不同态镉水平对大米镉含量影响存在差异，其中，有效态镉呈正向关系，其他形态镉的影响尚需进一步明确。

各变量投影重要性指标与载荷，见图3。

图3 各解释变量及所属区块与反应变量关系图

结合图3a与图3c可见，大米镉水平与有效态镉水平关系最为密切，且呈正向关联，与酸碱度、交换性酸度关系密切程度次之，且呈负向关联，与碳酸盐态镉和总镉水平稍呈负向关联，其关系密切程度较弱；而容重、有机质、有机结合态镉与大米镉水平关系不甚密切。由图3b可见，相对于土壤理化特性而言，土壤中的各态镉水平对大米镉水平影响稍强。

为了便于MB-PLSR与传统PLSR比较，拟从成分数nt、回归决定系数与预测决定系数三方面来评价两种方法的优劣。从原始样本中，按照20%的比例随机抽取样本，作为训练样本，余下的样本作为验证样本，分别用MB-PLSR和PLSR进行数据拟合与预测，重复100次，取的平均数。之后，与此类似，每次将训练样本的比例提高5%，而验证样本比例相应降低5%，直至训练样本比例达到80%为止。在不同训练样本比例下，两种方法所提取的成分数nt、回归决定系数与预测决定系数见图4。

图4 不同训练样本比例下MB-PLSR与PLSR的成分数与模型决定系数

由图4a可见，MB-PLSR提取的成分数一致地少于PLSR。这表明MB-PLSR可以更有效地压缩解释变量空间维度，具有更强的信息综合能力。由图4b可见，随着训练样本比例的上升，两种方法的回归决定系数呈下降趋势，预测决定系数则呈上升趋势，并且回归决定系数一致地高于预测决定系数。两种方法相较而言，无论在回归决定系数方面，或是在预测决定系数方面，MB-PLSR均要优于PLSR。这提示MB-PLSR通过区块成分的提取，可以更为有效地剔除原始数据中的部分噪声干扰，具有更好的模型解释与预测能力。

结 论

本文通过采用多区块偏最小二乘回归对食品重金属污染进行分析，可以发现，MB-PLSR可以在分析各类因素作用的基础上，较好地确定各变量区块影响大米重金属含量的重要性。与传统的偏最小二乘回归相比较，MB-PLSR具有更强的信息综合能力，模型拟合与预测精度也有所提高，并且，可以从变量、区块、成分三个层面，对结果给予更为清晰、简便与合理的解释。

对复杂数据而言，MB-PLSR无需对解释变量进行筛选，仅需按照相近内涵，事先对解释变量加以分类，划分为多个变量区块。一方面，通过各区块变量信息的综合提取，反映相应区块的内涵意义与潜在结构，以便分析各解释变量在区块中的影响程度与重要性；另一方面，通过构建全局成分与反应变量之间的回归模型，反映各区块对反应变量的影响程度与重要性，从而，间接地反映各解释变量对反应变量的影响与作用。可见，MB-PLSR通过利用变量区块的先验知识，可以大幅度地降低模型建构的复杂性，更好地符合与利用数据来源的自然结构，进而，达到简化模型，整体分析的目的。

需要注意的是，MB-PLSR尚存在三个方面的不足。一是，良好的变量区块必须依赖于坚实的专业理论知识，变量的不良区块会直接影响到MB-PLSR的分析效果；二是，全局成分的权重向量正交，而各解释变量区块成分的权重向量并不正交，这将导致解释变量区块的信息提取，存在着部分信息交叉，给在变量层面的解释带来一定困难；三是，该方法只能用于构建较简单的潜结构关系，不适于分析具有更复杂路径关系的高维数据，此时，需借助结构方程模型、偏最小二乘路径模型等其他统计分析方法来予以处理。

1.Roover KD，Ceulemans E，Timmerman ME.Modeling differences in the dimensionality of multiblock data by means of clusterwise simultaneous component analysis.Psychometricka，2013，78（4）：648-668.

2.Vivien M，Verron T，Sabatier R.Comparing and predicting sensory profiles by NIRS：use of the GOMCIA and GOMCIA-PLS multi-block methods.Journal of Chemometrics，2005，19，162-170.

3.Bougeard S，Qannari E，Lupo C，et al.From multiblock partial least squares to multiblock redundancy analysis，a continuum approach.Informatica，2011，22（1）：11-26.

4.Kramer N，Sugiyama M.The Degrees of Freedom of Partial Least Squares Regression.Journal of American Statistics Association，2011，106（1）：697-705.

5.Alloway BJ.Heavy Metals in Soils.Glasgow，Chapman＆Hall，1995.

6.Wangen LE，Kowalski BR.A multiblock partial least squares algorithm for investigating complex chemical systems.Journal of Chemometrics，1988，3：3-20.

7.蒋红卫，夏结来，李园，等.偏最小二乘回归的离群点检测方法.中国卫生统计，2007，24（8）：372-374.

8.蒋定国，李宁，杨杰.2010年我国食品化学污染物风险监测概况、存在问题及建议.中国食品卫生杂志，2012，24（3）：259-264.

9.WHO.Food Safety Risk Analysis，Rome.Italy，FAO，2009.

10.刘剑锋，谷宁，张可慧.土壤重金属空间分异及迁移研究进展与展望.地理与地理信息科学，2012，28（2）：99-103.

（责任编辑：郭海强）

Multiblock Partial Least Squares Regression Model for Environment-Food Heavy Metal Transfer

Jiang Hongwei，Zhang Lei，Yin Ping（Department of Epidemiology and Health Statistics，Tongji College，Huazhong University of Science and Technology（430030），Wuhan）

ObjectiveTo explore multiblock partial least squares regression（MB-PLSR）that deal with multiple variable blocks in complex data，and apply this statistical method to modeling environment-food heavy metal transfer.MethodsThe influence factors of cadmium（Cd）transfer from environment to rice were divided into two blocks：soil physical-chemical variable block and multi-state Cd variable block.MB-PLSR was used for modeling environment-food Cd transfer，and was compared with classical partial least squares regression（PLSR）in their performance.ResultsIn terms of the dimensional reduction，model prediction and interpretation，MB-PLSR is superior to PLSR.ConclusionAs a practical statistical method of soft modeling for handling complex data with multiple variable block structure，MB-PLSR has several technical advantages in information extraction and model interpretability.

Variable block；Component；Heavy metal；Partial least squares regression

*国家自然科学基金项目（81373104）；中央高校基本科研业务资助（2012QN241）

1.华中科技大学同济医学院公共卫生学院流行病学与卫生统计学系（430030）

2.国家食品安全风险评估中心

△通信作者：蒋红卫，E-mail：jhwccc＠sina.com